2020九年级数学上册 矩形的性质与判定课时练习 （新版）北师大版 9页

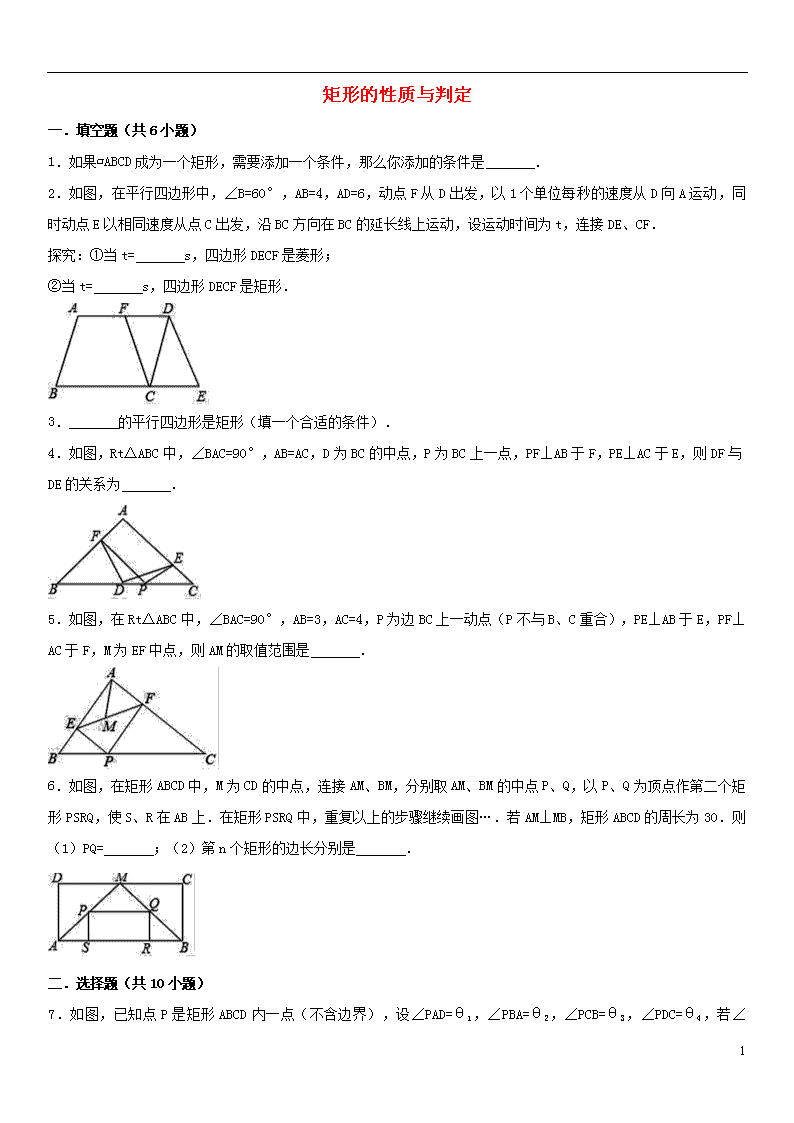
矩形的性质与判定 一．填空题（共6小题）‎ ‎1．如果▱ABCD成为一个矩形，需要添加一个条件，那么你添加的条件是　 　．‎ ‎2．如图，在平行四边形中，∠B=60°，AB=4，AD=6，动点F从D出发，以1个单位每秒的速度从D向A运动，同时动点E以相同速度从点C出发，沿BC方向在BC的延长线上运动，设运动时间为t，连接DE、CF．‎ 探究：①当t=　 　s，四边形DECF是菱形；‎ ‎②当t=　 　s，四边形DECF是矩形．‎ ‎3．　 　的平行四边形是矩形（填一个合适的条件）．‎ ‎4．如图，Rt△ABC中，∠BAC=90°，AB=AC，D为BC的中点，P为BC上一点，PF⊥AB于F，PE⊥AC于E，则DF与DE的关系为　 　．‎ ‎5．如图，在Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点（P不与B、C重合），PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的取值范围是　 　．‎ ‎6．如图，在矩形ABCD中，M为CD的中点，连接AM、BM，分别取AM、BM的中点P、Q，以P、Q为顶点作第二个矩形PSRQ，使S、R在AB上．在矩形PSRQ中，重复以上的步骤继续画图…．若AM⊥MB，矩形ABCD的周长为30．则（1）PQ=　 　；（2）第n个矩形的边长分别是　 　．‎ 二．选择题（共10小题）‎ ‎7．如图，已知点P是矩形ABCD内一点（不含边界），设∠PAD=θ1，∠PBA=θ2，∠PCB=θ3，∠PDC=θ4，若∠‎ 8‎ APB=80°，∠CPD=50°，则（　　）‎ A．（θ1+θ4）﹣（θ2+θ3）=30° B．（θ2+θ4）﹣（θ1+θ3）=40°‎ C．（θ1+θ2）﹣（θ3+θ4）=70° D．（θ1+θ2）+（θ3+θ4）=180°‎ ‎8．矩形具有而一般的平行四边形不一定具有的特征（　　）‎ A．对角相等 B．对角线相等 C．对角线互相平分 D．对边相等 ‎9．如图，矩形ABCD中，AB=3，BC=4，EB∥DF且BE与DF之间的距离为3，则AE的长是（　　）‎ A． B． C． D．‎ ‎10．如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是（　　）‎ A． B． C． D．不确定 ‎11．如图，在矩形ABCD中，AD=30，AB=20，若点E、F三等分对角线AC，则△ABE的面积为（　　）‎ A．60 B．‎100 ‎C．150 D．200‎ ‎12．如图，利用四边形的不稳定性改变矩形ABCD的形状，得到▱A1BCD1，若▱A1BCD1的面积是矩形ABCD面积的一半，则∠ABA1的度数是（　　）‎ A．15° B．30° C．45° D．60°‎ 8‎ ‎13．如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB=60°，AC=‎4cm，则矩形ABCD的面积为（　　）‎ A．‎12cm2 B．‎4cm‎2 ‎C．‎8cm2 D．‎6cm2‎ ‎14．如图，在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=60°，AB=2，则AC的长是（　　）‎ A．4 B．‎6 ‎C．8 D．10‎ ‎15．如图，矩形ABCD中，AB=4，BC=2，O为对角线AC的中点，点P、Q分别从A和B两点同时出发，在边AB和BC上匀速运动，并且同时到达终点B、C，连接PO、QO并延长分别与CD、DA交于点M、N．在整个运动过程中，图中阴影部分面积的大小变化情况是（　　）‎ A．一直增大 B．一直减小 C．先减小后增大 D．先增大后减小 ‎16．如图，矩形ABCD由3×4个小正方形组成，此图中不是正方形的矩形有（　　）‎ A．34个 B．36个 C．38个 D．40个　‎ 三．解答题（共5小题）‎ ‎17．如图所示，在矩形ABCD中，对角线AC、BD相交于点O，CE∥DB，交AD的延长线于点E，试说明AC=CE．‎ 8‎ ‎18．如图，在长方形ABCD中，点E，F分别在边AB和BC上，∠AEF的平分线与边AD交于点G，线段EG的反向延长线与∠EFB的平分线交于点H．‎ ‎（1）当∠BEF=50°（图1），试求∠H的度数．‎ ‎（2）当E，F在边AB和BC上任意移动时（不与点B重合）（图2），∠H的大小是否变化？若变化，请说明理由；若不变化，求出∠H的度数．‎ ‎19．如图：矩形ABCD中，AB=2，BC=5，E、G分别在AD、BC上，且DE=BG=1．‎ ‎（1）判断△BEC的形状，并说明理由？‎ ‎（2）判断四边形EFGH是什么特殊四边形？并证明你的判断．‎ ‎20．已知：如图，四边形ABCD是矩形（AD＞AB），点E在BC上，且AE=AD，DF⊥AE，垂足为F，‎ 求证：DF=AB．‎ ‎21．如图，在矩形ABCD中，E是BC上的一点，且AE=AD，又DF⊥AE于点F ‎（1）求证：CE=EF；‎ ‎（2）若EF=2，CD=4，求矩形ABCD的面积．‎ ‎　‎ 8‎ 参考答案与试题解析 一．填空题 ‎1．∠A=90°‎ ‎2．①4；②2．‎ ‎3．有一个角是直角（答案不唯一）‎ ‎4．DF=DE且DF⊥DE ‎5．≤AM＜2‎ ‎6．10×，5×‎ 二．选择题 ‎7．A ‎8．B ‎9．C ‎10．C ‎11．B ‎12．D ‎13．B ‎14．A ‎15．C ‎16．D 三．解答题 ‎17．‎ 分析:由矩形的性质，可得AC=BD，欲求AC=CE，证BD=CE即可．可通过证四边形BDEC是平行四边形，从而得出BD=CE的结论．‎ 解答: 解：在矩形ABCD中，AC=BD，‎ AD∥BC．‎ 又∵CE∥DB，‎ ‎∴四边形BDEC是平行四边形．‎ ‎∴BD=EC，‎ ‎∴AC=CE．‎ ‎　‎ 8‎ ‎18．‎ 分析:（1）根据三角形的内角和是180°，可求∠EFB=40°，所以∠EFH=20°，又由平角定义，可求∠AEF=130°，所以∠GEF=65°，又根据三角形的外角等于与它不相邻的两内角之和，可得∠H=45度．‎ ‎（2）运用（1）中的计算方法即可得到，∠H的大小不发生变化．‎ 解答: 解：（1）∵∠B=90°，∠BEF=50°，‎ ‎∴∠EFB=40°．‎ ‎∵GE是∠AEF的平分线，HF是∠BFE的平分线，‎ ‎∴∠GEF=65°，∠EFH=20°．‎ ‎∵∠GEF=∠H+∠EFH，‎ ‎∴∠H=65°﹣20°=45°．‎ ‎（2）不变化．‎ ‎∵∠B=90°，‎ ‎∴∠EFB=90°﹣∠BEF．‎ ‎∵GE是∠AEF的平分线，HF是∠BFE的平分线，‎ ‎∴∠GEF=∠AEF=（180°﹣∠BEF），∠EFH=∠EFB=（90°﹣∠BEF）．‎ ‎∵∠GEF=∠H+∠EFH，‎ ‎∴∠H=∠GEF﹣∠EFH=（180°﹣∠BEF）﹣（90°﹣∠BEF）=45°．‎ ‎　‎ ‎19．‎ 分析:（1）根据矩形性质得出CD=2，根据勾股定理求出CE和BE，求出CE2+BE2的值，求出BC2，根据勾股定理的逆定理求出即可；‎ ‎（2）根据矩形的性质和平行四边形的判定，推出平行四边形DEBG和AECG，推出EH∥FG，EF∥HG，推出平行四边形EFGH，根据矩形的判定推出即可．‎ 解答:解：（1）△BEC是直角三角形：理由如下：‎ 8‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠ADC=∠ABP=90°，AD=BC=5，AB=CD=2，‎ 由勾股定理得：CE===，‎ 同理BE=2，‎ ‎∴CE2+BE2=5+20=25，‎ ‎∵BC2=52=25，‎ ‎∴BE2+CE2=BC2，‎ ‎∴∠BEC=90°，‎ ‎∴△BEC是直角三角形．‎ ‎（2）四边形EFGH为矩形，理由如下：‎ ‎∵四边形ABCD是矩形，‎ ‎∴AD=BC，AD∥BC，‎ ‎∵DE=BG，‎ ‎∴四边形DEBG是平行四边形，‎ ‎∴BE∥DG，‎ ‎∵AD=BC，AD∥BC，DE=BG，‎ ‎∴AE=CG，‎ ‎∴四边形AECG是平行四边形，‎ ‎∴AG∥CE，‎ ‎∴四边形EFGH是平行四边形，‎ ‎∵∠BEC=90°，‎ ‎∴平行四边形EFGH是矩形．‎ ‎　‎ ‎20．‎ 分析:根据矩形性质得出∠B=∠DFA=90°，AD∥BC，求出∠DAF=∠AEB，△AFD≌△EBA，根据全等得出即可．‎ 解答:证明：∵四边形ABCD是矩形，DF⊥AE，‎ ‎∴∠B=∠DFA=90°，AD∥BC，‎ ‎∴∠DAF=∠AEB，‎ 在△AFD和△EBA中，‎ 8‎ ‎，‎ ‎∴△AFD≌△EBA（AAS），‎ ‎∴DF=AB．‎ ‎　‎ ‎21．‎ 分析:（1）连接DE，利用矩形的性质，则可证得Rt△ABE≌Rt△DFA，进一步可证得Rt△DFE≌Rt△DCE，则可证得结论；‎ ‎（2）设BE=x，则AF=x，AE=x+2，在Rt△ABE中，利用勾股定理，可求得AE，则可求得BC的长，可求得矩形ABCD的面积．‎ 解答:证明：‎ ‎（1）如图，连接DE，‎ ‎∵四边形ABCD是矩形，‎ ‎∴AD∥BC，‎ ‎∴∠DAF=∠AEB，‎ ‎∵DF⊥AE，‎ ‎∴∠AFD=∠B=90°．‎ 又∵AD=AE，‎ ‎∴Rt△ABE≌Rt△DFA．‎ ‎∴AB=CD=DF．‎ 又∵∠DFE=∠C=90°，DE=DE，‎ ‎∴Rt△DFE≌Rt△DCE．‎ ‎∴EC=EF；‎ ‎（2）∵EF=EC=2，CD=AB=4，‎ ‎∴设BE=x，则AF=x，AE=x+2．‎ 在Rt△ABE中，∵BE2+AB2=AE2，‎ ‎∴42+x2=（x+2）2．‎ 解这个方程得：x=3，‎ ‎∴BC=5．‎ ‎∴矩形ABCD的面积=5×4=20．‎ 8‎ 8‎