2020年中考数学试题【附解析】 36页

‎2020年中考数学押题卷 一、选择题：本大题有10个小题，每小题3分，共30分。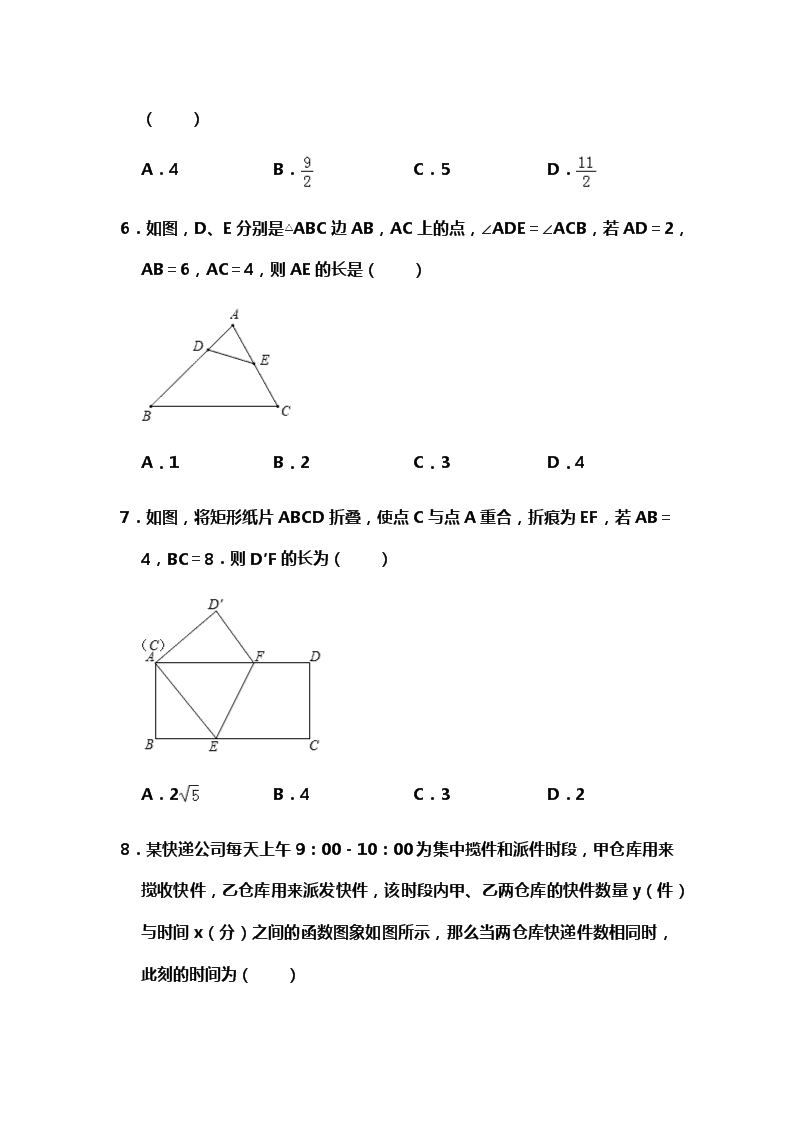‎ ‎1．在﹣4、﹣、0、4这四个数中，最小的数是（　　）‎ A．4 B．0 C．﹣ D．﹣4‎ ‎2．若关于x的一元二次方程kx2﹣x﹣＝0有实数根，则实数k的取值范围是（　　）‎ A．k＝0 B．k≥﹣ C．k≥﹣且k≠0 D．k＞﹣‎ ‎3．如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝100°，则∠α＝（　　）‎ A．80° B．100° C．120° D．160°‎ ‎4．某车间接了生产12000只口罩的订单，加工4800个口罩后，采用了的新的工艺，效率是原来的1.5倍，任务完成后发现比原计划少用了2个小时．设采用新工艺之前每小时可生产口罩x个，依据题意可得方程（　　）‎ A．＝2 B．＝2 ‎ C．＝2 D．＝2‎ ‎5‎ ‎．一组数据2，3，5，x，7，4，6，9的众数是4，则这组数据的中位数是（　　）‎ A．4 B． C．5 D．‎ ‎6．如图，D、E分别是△ABC边AB，AC上的点，∠ADE＝∠ACB，若AD＝2，AB＝6，AC＝4，则AE的长是（　　）‎ A．1 B．2 C．3 D．4‎ ‎7．如图，将矩形纸片ABCD折叠，使点C与点A重合，折痕为EF，若AB＝4，BC＝8．则D′F的长为（　　）‎ A．2 B．4 C．3 D．2‎ ‎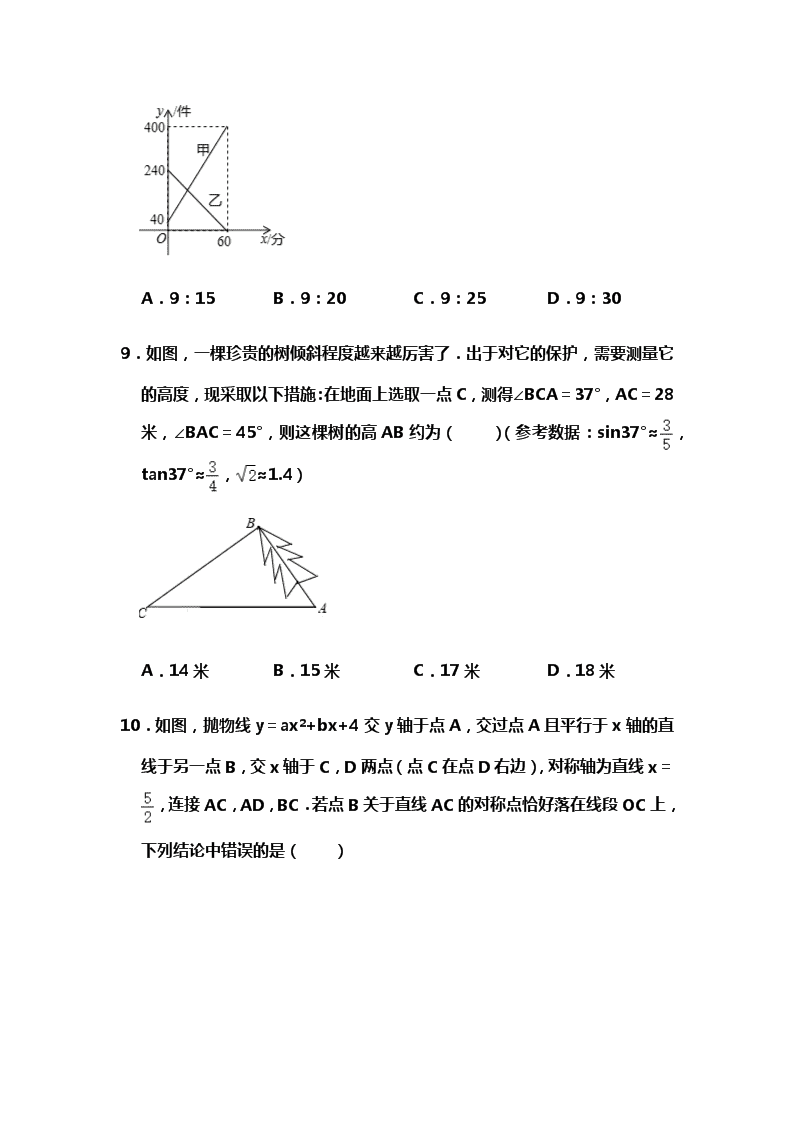8．某快递公司每天上午9：00﹣10：00为集中揽件和派件时段，甲仓库用来搅收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，那么当两仓库快递件数相同时，此刻的时间为（　　）‎ A．9：15 B．9：20 C．9：25 D．9：30‎ ‎9．如图，一棵珍贵的树倾斜程度越来越厉害了．出于对它的保护，需要测量它的高度，现采取以下措施：在地面上选取一点C，测得∠BCA＝37°，AC＝28米，∠BAC＝45°，则这棵树的高AB约为（　　）（参考数据：sin37°≈，tan37°≈，≈1.4）‎ A．14米 B．15米 C．17米 D．18米 ‎10．如图，抛物线y＝ax2+bx+4交y轴于点A，交过点A且平行于x轴的直线于另一点B，交x轴于C，D两点（点C在点D右边），对称轴为直线x＝，连接AC，AD，BC．若点B关于直线AC的对称点恰好落在线段OC上，下列结论中错误的是（　　）‎ A．点B坐标为（5，4） B．AB＝AD C．a＝﹣ D．OC•OD＝16‎ 二、填空题：本大题有6个小题，每小题4分，共24分，‎ ‎11．分解因式：a3+ab2﹣2a2b＝　 　．‎ ‎12．国学经典《声律启蒙》中有这样一段话：“斜对正，假对真，韩卢对苏雁，陆橘对庄椿”，现有四张卡片依次写有一“斜”、“正”、“假”、“真”，四个字（4张卡片除了书写汉字不同外其他完全相同），现从四张卡片中随机抽取两张，则抽到的汉字恰为相反意义的概率是　　．‎ ‎13．用一个半径为15、圆心角为120°的扇形围成一个圆锥，则这个圆锥的底面半径是　　．‎ ‎14．如图，等腰△ABC的周长是36cm，底边为10cm，则底角的正弦值是　 　．‎ ‎15．如图，在Rt△ABO中，∠OBA＝90°，A（4，4），点C在边AB上，且 ‎＝，点D为OB的中点，点P为边OA上的动点，当点P在OA上移动时，使四边形PDBC周长最小的点P的坐标为　 　．‎ ‎16．如图，小聪用一张面积为1的正方形纸片，按如下方式操作：‎ ‎①将正方形纸片四角向内折叠，使四个顶点重合，展开后沿折痕剪开，把四个等腰直角三角形扔掉；‎ ‎②在余下纸片上依次重复以上操作，当完成第2019次操作时，余下纸片的面积为　 　．‎ 三、解答题：本大题有7个小题，共66分.‎ ‎17．化简：‎ ‎18.某校组织学生开展了“2020新冠疫情”相关的手抄报竞赛．对于手抄报的主题，组织者提出了两条指导性建议：‎ ‎（1）A类“武汉加油”、B类“最美逆行者”、C类“万众一心抗击疫情”、D类“如何预防新型冠状病毒”4个中任选一个；‎ ‎（2）E类为自拟其它与疫情相关的主题．‎ 评奖之余，为了解学生的选题倾向，发掘出最能引发学生触动的主题素材，组织者随机抽取了部分作品进行了统计，并将统计结果绘制成了如下两幅尚不完整的统计图．‎ 请根据以上信息回答：‎ ‎（1）本次抽样调查的学生总人数是　 　，并补全条形统计图；‎ ‎（2）扇形统计图中，“C”对应的扇形圆心角的度数是　 　，x＝　 　，y﹣z＝　 　；‎ ‎（3）本次抽样调查中，“学生手抄报选题”最为广泛的是　 　类．（填字母）‎ ‎19.如图，在△ABC中，AB＝AC，D是AB上一点，以点D为圆心，AC为半径画弧交BA的延长线于点E，连接CD，作EF∥CD，交∠EAC的平分线于点F，连接CF．‎ ‎（1）求证：△BCD≌△AFE；‎ ‎（2）若AC＝6，∠BAC＝30°，求四边形CDEF的面积S四边形CDEF．‎ ‎20.湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了20000kg淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本=放养总费用+收购成本）．‎ ‎（1）设每天的放养费用是a万元，收购成本为b万元，求a和b的值；‎ ‎（2）设这批淡水鱼放养t天后的质量为m（kg），销售单价为y元/kg．根据以往经验可知：m与t的函数关系为；y与t的函数关系如图所示．‎ ‎①分别求出当0≤t≤50和50＜t≤100时，y与t的函数关系式；‎ ‎②设将这批淡水鱼放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出最大值．（利润=销售总额﹣总成本）‎ ‎21．如图，在▱ABCD中，对角线AC，BD相交于点O，过点O作MN⊥BD，分别交AD，BC于点M，N．‎ ‎（1）求证：OM＝ON；‎ ‎（2）求证：四边形BNDM是菱形．‎ ‎22.已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．‎ ‎（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；‎ ‎（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；‎ ‎（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．‎ ‎23‎ ‎．如图，已知半圆O的直径DE=12cm，在△ABC中，∠ACB=90°，∠ABC=30°，BC=12cm，半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上．设运动时间为t（s），当t=0s时，半圆O在△ABC的左侧，OC=8cm．‎ ‎（1）当t为何值时，△ABC的一边所在直线与半圆O所在的圆相切？‎ ‎（2）当△ABC的一边所在直线与半圆O所在的圆相切时，如果半圆O与直线DE围成的区域与△ABC三边围成的区域有重叠部分，求重叠部分的面积．‎ 解析 一、选择题：本大题有10个小题，每小题3分，共30分。‎ ‎1．在﹣4、﹣、0、4这四个数中，最小的数是（　　）‎ A．4 B．0 C．﹣ D．﹣4‎ 解：﹣4＜﹣＜0＜4，‎ ‎∴在﹣4、﹣、0、4这四个数中，最小的数是﹣4．‎ 故选：D．‎ ‎2．若关于x的一元二次方程kx2﹣x﹣＝0有实数根，则实数k的取值范围是（　　）‎ A．k＝0 B．k≥﹣ C．k≥﹣且k≠0 D．k＞﹣‎ 解：由题意可知：△＝（﹣1）2﹣4×k×（）＝1+3k≥0，‎ ‎∴k≥，‎ ‎∵k≠0，‎ ‎∴k≥且k≠0，‎ 故选：C．‎ ‎3．如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝100°，则∠α＝（　　）‎ A．80° B．100° C．120° D．160°‎ 解：优弧AB上任取一点D，连接AD，BD，．‎ ‎∵四边形ACBD内接与⊙O，∠C＝100°，‎ ‎∴∠ADB＝180°﹣∠C＝180°﹣100°＝80°，‎ ‎∴∠AOB＝2∠ADB＝2×80°＝160°．‎ 故选：D．‎ ‎4．某车间接了生产12000只口罩的订单，加工4800个口罩后，采用了的新的工艺，效率是原来的1.5倍，任务完成后发现比原计划少用了2个小时．设采用新工艺之前每小时可生产口罩x个，依据题意可得方程（　　）‎ A．＝2 B．＝2 ‎ C．＝2 D．＝2‎ 解：设采用新工艺之前每小时可生产口罩x个，则采用新工艺之后每小时可生产口罩1.5x个，‎ 依题意，得：﹣＝2．‎ 故选：D．‎ ‎5．一组数据2，3，5，x，7，4，6，9的众数是4，则这组数据的中位数是（　　）‎ A．4 B． C．5 D．‎ 解：∵这组数据的众数4，‎ ‎∴x＝4，‎ 将数据从小到大排列为：2，3，4，4，5，6，7，9‎ 则中位数为：4.5．‎ 故选：B．‎ ‎6．如图，D、E分别是△ABC边AB，AC上的点，∠ADE＝∠ACB，若AD＝2，AB＝6，AC＝4，则AE的长是（　　）‎ A．1 B．2 C．3 D．4‎ 解：∵∠ADE＝∠ACB，∠A＝∠A，‎ ‎∴△ADE∽△ACB，‎ ‎∴＝，即＝，‎ 解得，AE＝3，‎ 故选：C．‎ ‎7‎ ‎．如图，将矩形纸片ABCD折叠，使点C与点A重合，折痕为EF，若AB＝4，BC＝8．则D′F的长为（　　）‎ A．2 B．4 C．3 D．2‎ 解：连接AC交EF于点O，如图所示：‎ ‎∵四边形ABCD是矩形，‎ ‎∴AD＝BC＝8，∠B＝∠D＝90°，‎ AC＝＝＝4，‎ ‎∵折叠矩形使C与A重合时，EF⊥AC，AO＝CO＝AC＝2，‎ ‎∴∠AOF＝∠D＝90°，∠OAF＝∠DAC，‎ ‎∴则Rt△FOA∽Rt△ADC，‎ ‎∴＝，即：＝，‎ 解得：AF＝5，‎ ‎∴D′F＝DF＝AD﹣AF＝8﹣5＝3，‎ 故选：C．‎ ‎8．某快递公司每天上午9：00﹣10：00为集中揽件和派件时段，甲仓库用来搅收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，那么当两仓库快递件数相同时，此刻的时间为（　　）‎ A．9：15 B．9：20 C．9：25 D．9：30‎ 解：设甲仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y1＝k1x+40，根据题意得60k1+40＝400，解得k1＝6，‎ ‎∴y1＝6x+40；‎ 设乙仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y2＝k2x+240，根据题意得60k2+240＝0，解得k2＝﹣4，‎ ‎∴y2＝﹣4x+240，‎ 联立，解得，‎ ‎∴此刻的时间为9：20．‎ 故选：B．‎ ‎9．如图，一棵珍贵的树倾斜程度越来越厉害了．出于对它的保护，需要测量它的高度，现采取以下措施：在地面上选取一点C，测得∠BCA＝37°，AC＝28米，∠BAC＝45°，则这棵树的高AB约为（　　）（参考数据：sin37°≈，tan37°≈，≈1.4）‎ A．14米 B．15米 C．17米 D．18米 解：如图，作BH⊥AC于H．‎ ‎∵∠BCH＝37°，∠BHC＝90°，‎ 设BH＝xm，‎ ‎∴CH＝＝＝，‎ ‎∵∠A＝45°，‎ ‎∴AH＝BH＝x，‎ ‎∴x+x＝28，‎ ‎∴x＝12，‎ ‎∴AB＝AH＝×12≈17（m）‎ 故选：C．‎ ‎10．如图，抛物线y＝ax2+bx+4交y轴于点A，交过点A且平行于x轴的直线于另一点B，交x轴于C，D两点（点C在点D右边），对称轴为直线x＝，连接AC，AD，BC．若点B关于直线AC的对称点恰好落在线段OC上，下列结论中错误的是（　　）‎ A．点B坐标为（5，4） B．AB＝AD C．a＝﹣ D．OC•OD＝16‎ 解：∵抛物线y＝ax2+bx+4交y轴于点A，‎ ‎∴A（0，4），‎ ‎∵对称轴为直线x＝，AB∥x轴，‎ ‎∴B（5，4）．‎ 故A无误；‎ 如图，过点B作BE⊥x轴于点E，‎ 则BE＝4，AB＝5，‎ ‎∵AB∥x轴，‎ ‎∴∠BAC＝∠ACO，‎ ‎∵点B关于直线AC的对称点恰好落在线段OC上，‎ ‎∴∠ACO＝∠ACB，‎ ‎∴∠BAC＝∠ACB，‎ ‎∴BC＝AB＝5，‎ ‎∴在Rt△BCE中，由勾股定理得：EC＝3，‎ ‎∴C（8，0），‎ ‎∵对称轴为直线x＝，‎ ‎∴D（﹣3，0）‎ ‎∵在Rt△ADO中，OA＝4，OD＝3，‎ ‎∴AD＝5，‎ ‎∴AB＝AD，‎ 故B无误；‎ 设y＝ax2+bx+4＝a（x+3）（x﹣8），‎ 将A（0，4）代入得：4＝a（0+3）（0﹣8），‎ ‎∴a＝﹣，‎ 故C无误；‎ ‎∵OC＝8，OD＝3，‎ ‎∴OC•OD＝24，‎ 故D错误．‎ 综上，错误的只有D．‎ 故选：D．‎ 二、填空题：本大题有6个小题，每小题4分，共24分，‎ ‎11．分解因式：a3+ab2﹣2a2b＝　 　．‎ 解：a3+ab2﹣2a2b，‎ ‎＝a（a2+b2﹣2ab），‎ ‎＝a（a﹣b）2．‎ ‎12．国学经典《声律启蒙》中有这样一段话：“斜对正，假对真，韩卢对苏雁，陆橘对庄椿”，现有四张卡片依次写有一“斜”、“正”、“假”、“真”，四个字（4张卡片除了书写汉字不同外其他完全相同），现从四张卡片中随机抽取两张，则抽到的汉字恰为相反意义的概率是　　．‎ 解：设“斜”、“正”、“假”、“真”分别为A，B，C，D，画树状图得：‎ 由树状图可知共有12种等可能的结果数，其中汉字恰为相反意义的有4种，‎ 所以抽到的汉字恰为相反意义的概率＝＝，‎ 故答案为：．‎ ‎13．用一个半径为15、圆心角为120°的扇形围成一个圆锥，则这个圆锥的底面半径是　　．‎ 解：设该圆锥底面圆的半径为r，‎ 根据题意得2πr＝，解得r＝5，‎ 即该圆锥底面圆的半径为5．‎ ‎14．如图，等腰△ABC的周长是36cm，底边为10cm，则底角的正弦值是　 　．‎ 解：因为等腰三角形ABC的周长是36cm，底边为10cm，‎ 所以AB＝AC＝13cm 过点A做AD⊥BC，垂足为D．‎ ‎∴BD＝BC＝5cm 在Rt△ABD中，AD＝‎ ‎＝‎ ‎＝12（cm）‎ sinB＝＝．‎ 故答案为：‎ ‎15．如图，在Rt△ABO中，∠OBA＝90°，A（4，4），点C在边AB上，且＝，点D为OB的中点，点P为边OA上的动点，当点P在OA上移动时，使四边形PDBC周长最小的点P的坐标为　 　．‎ 解：∵在Rt△ABO中，∠OBA＝90°，A（4，4），‎ ‎∴AB＝OB＝4，∠AOB＝45°，‎ ‎∵＝，点D为OB的中点，‎ ‎∴BC＝3，OD＝BD＝2，‎ ‎∴D（0，2），C（4，3），‎ 作D关于直线OA的对称点E，连接EC交OA于P，‎ 则此时，四边形PDBC周长最小，E（0，2），‎ ‎∵直线OA 的解析式为y＝x，‎ 设直线EC的解析式为y＝kx+b，‎ ‎∴，‎ 解得：，‎ ‎∴直线EC的解析式为y＝x+2，‎ 解得，，‎ ‎∴P（，），‎ ‎16．如图，小聪用一张面积为1的正方形纸片，按如下方式操作：‎ ‎①将正方形纸片四角向内折叠，使四个顶点重合，展开后沿折痕剪开，把四个等腰直角三角形扔掉；‎ ‎②在余下纸片上依次重复以上操作，当完成第2019次操作时，余下纸片的面积为　 　．‎ 解：正方形纸片四角向内折叠，使四个顶点重合，展开后沿折痕剪开，‎ 第一次：余下面积，‎ 第二次：余下面积，‎ 第三次：余下面积，‎ 当完成第2019次操作时，余下纸片的面积为 三、解答题：本大题有7个小题，共66分.‎ ‎17．化简：‎ 解：原式＝[+]÷‎ ‎＝（+）•（x+1）‎ ‎＝•（x+1）‎ ‎＝，‎ ‎18.某校组织学生开展了“2020新冠疫情”相关的手抄报竞赛．对于手抄报的主题，组织者提出了两条指导性建议：‎ ‎（1）A类“武汉加油”、B类“最美逆行者”、C类“万众一心抗击疫情”、D类“如何预防新型冠状病毒”4个中任选一个；‎ ‎（2）E类为自拟其它与疫情相关的主题．‎ 评奖之余，为了解学生的选题倾向，发掘出最能引发学生触动的主题素材，组织者随机抽取了部分作品进行了统计，并将统计结果绘制成了如下两幅尚不完整的统计图．‎ 请根据以上信息回答：‎ ‎（1）本次抽样调查的学生总人数是　 　，并补全条形统计图；‎ ‎（2）扇形统计图中，“C”对应的扇形圆心角的度数是　 　，x＝　 　，y﹣z＝　 　；‎ ‎（3）本次抽样调查中，“学生手抄报选题”最为广泛的是　 　类．（填字母）‎ 解：（1）调查的学生总人数：30÷25%＝120（人），‎ ‎120×20%＝24（人），‎ ‎120﹣30﹣36﹣24﹣18＝12（人），‎ 如图所示：‎ ‎（2）“C”对应的扇形圆心角的度数是：360°×20%＝72°，‎ x%＝×100%＝30%，y%＝‎ ‎×100%＝15%，z%＝1﹣30%﹣15%﹣25%﹣20%＝10%，‎ 故x＝30，y﹣z＝10﹣5＝5，‎ 故答案为：72°，30，5；‎ ‎（3）由（2）中所求，可得出：“学生手抄报选题”最为广泛的是B类．‎ 故答案为：B．‎ ‎19.如图，在△ABC中，AB＝AC，D是AB上一点，以点D为圆心，AC为半径画弧交BA的延长线于点E，连接CD，作EF∥CD，交∠EAC的平分线于点F，连接CF．‎ ‎（1）求证：△BCD≌△AFE；‎ ‎（2）若AC＝6，∠BAC＝30°，求四边形CDEF的面积S四边形CDEF．‎ 解：（1）∵AB＝AC，‎ ‎∴∠B＝∠ACB，‎ ‎∵∠EAC＝∠B+∠ACB，‎ ‎∴∠EAC＝2∠B，‎ ‎∵∠1＝∠2，‎ ‎∴∠EAC＝2∠1，‎ ‎∴∠B＝∠1，‎ ‎∵EF∥CD，‎ ‎∴∠BDC＝∠AEF，‎ ‎∵AB＝AC＝DE，‎ ‎∴BD＝AE，‎ ‎∴△BCD≌△AFE（ASA）；‎ ‎（2）如图，过A作AH⊥CF，垂足为H，‎ ‎∵△BCD≌△AFE，‎ ‎∴CD＝EF，‎ 又∵EF∥CD，‎ ‎∴四边形CDEF是平行四边形，‎ ‎∴CF＝AB＝AC＝6，且CF∥AB，‎ ‎∵∠BAC＝30°，‎ ‎∴∠ACH＝30°，‎ ‎∴AH＝AC＝3，‎ ‎∴S四边形CDEF＝CF×AH＝6×3＝18．‎ ‎20.湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了20000kg淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本=放养总费用+收购成本）．‎ ‎（1）设每天的放养费用是a万元，收购成本为b万元，求a和b的值；‎ ‎（2）设这批淡水鱼放养t天后的质量为m（kg），销售单价为y元/kg．根据以往经验可知：m与t的函数关系为；y与t的函数关系如图所示．‎ ‎①分别求出当0≤t≤50和50＜t≤100时，y与t的函数关系式；‎ ‎②设将这批淡水鱼放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出最大值．（利润=销售总额﹣总成本）‎ 解：（1）由题意，得：，‎ 解得，‎ 答：a的值为0.04，b的值为30；‎ ‎（2）①当0≤t≤50时，设y与t的函数解析式为y=k1t+n1，‎ 将（0，15）、（50，25）代入，得：，‎ 解得：，‎ ‎∴y与t的函数解析式为y=t+15；‎ 当50＜t≤100时，设y与t的函数解析式为y=k2t+n2，‎ 将点（50，25）、（100，20）代入，得：，‎ 解得：，‎ ‎∴y与t的函数解析式为y=﹣t+30；‎ ‎②由题意，当0≤t≤50时，‎ W=20000（t+15）﹣（400t+300000）=3600t，‎ ‎∵3600＞0，‎ ‎∴当t=50时，W最大值=180000（元）；‎ 当50＜t≤100时，W=（100t+15000）（﹣t+30）﹣（400t+300000）‎ ‎=﹣10t2+1100t+150000‎ ‎=﹣10（t﹣55）2+180250，‎ ‎∵﹣10＜0，‎ ‎∴当t=55时，W最大值=180250（元），‎ 综上所述，放养55天时，W最大，最大值为180250元．‎ ‎21．如图，在▱ABCD中，对角线AC，BD相交于点O，过点O作MN⊥BD，分别交AD，BC于点M，N．‎ ‎（1）求证：OM＝ON；‎ ‎（2）求证：四边形BNDM是菱形．‎ 证明：（1）∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，OD＝OB，‎ ‎∴∠ADO＝∠CBO，‎ ‎∵MN⊥BD，‎ ‎∴∠MOD＝∠NOB＝90°，‎ 在△MOD和△NOB中 ‎∴△MOD≌△NOB（ASA）‎ ‎∴OM＝ON ‎（2）∵OM＝ON，‎ 又∵OD＝OB，‎ ‎∴四边形BNDM是平行四边形，‎ ‎∵MN⊥BD，‎ ‎∴平行四边形BNDM是菱形．‎ ‎22.已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．‎ ‎（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；‎ ‎（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；‎ ‎（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．‎ 解：（1）∵抛物线y=ax2+ax+b有一个公共点M（1，0），‎ ‎∴a+a+b=0，即b=﹣2a，‎ ‎∴y=ax2+ax+b=ax2+ax﹣2a=a（x+）2﹣，‎ ‎∴抛物线顶点D的坐标为（﹣，﹣）；‎ ‎（2）∵直线y=2x+m经过点M（1，0），‎ ‎∴0=2×1+m，解得m=﹣2，‎ ‎∴y=2x﹣2，‎ 则，‎ 得ax2+（a﹣2）x﹣2a+2=0，‎ ‎∴（x﹣1）（ax+2a﹣2）=0，‎ 解得x=1或x=﹣2，‎ ‎∴N点坐标为（﹣2，﹣6），‎ ‎∵a＜b，即a＜﹣2a，‎ ‎∴a＜0，‎ 如图1，设抛物线对称轴交直线于点E，‎ ‎∵抛物线对称轴为x=﹣=﹣，‎ ‎∴E（﹣，﹣3），‎ ‎∵M（1，0），N（﹣2，﹣6），‎ 设△DMN的面积为S，‎ ‎∴S=S△DEN+S△DEM=|（﹣2）﹣1|•|﹣﹣（﹣3）|=，‎ ‎（3）当a=﹣1时，‎ 抛物线的解析式为：y=﹣x2﹣x+2=﹣（x﹣）2+，‎ 有，‎ ‎﹣x2﹣x+2=﹣2x，‎ 解得：x1=2，x2=﹣1，‎ ‎∴G（﹣1，2），‎ ‎∵点G、H关于原点对称，‎ ‎∴H（1，﹣2），‎ 设直线GH平移后的解析式为：y=﹣2x+t，‎ ‎﹣x2﹣x+2=﹣2x+t，‎ x2﹣x﹣2+t=0，‎ ‎△=1﹣4（t﹣2）=0，‎ t=，‎ 当点H平移后落在抛物线上时，坐标为（1，0），‎ 把（1，0）代入y=﹣2x+t，‎ t=2，‎ ‎∴当线段GH与抛物线有两个不同的公共点，t的取值范围是2≤t＜．‎ ‎23．如图，已知半圆O的直径DE=12cm，在△ABC中，∠ACB=90°，∠ABC=30°，BC=12cm，半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上．设运动时间为t（s），当t=0s时，半圆O在△ABC的左侧，OC=8cm．‎ ‎（1）当t为何值时，△ABC的一边所在直线与半圆O所在的圆相切？‎ ‎（2）当△ABC的一边所在直线与半圆O所在的圆相切时，如果半圆O与直线DE围成的区域与△ABC三边围成的区域有重叠部分，求重叠部分的面积．‎ 解：（1）①如图，当点E与点C重合时，AC⊥OE，OC=OE=6cm，所以AC与半圆O所在的圆相切，此时点O运动了2cm，所求运动时间为：t==1（s）‎ ‎②如图，当点O运动到点C时，过点O作OF⊥AB，垂足为F．‎ 在Rt△FOB中，∠FBO=30°，OB=12cm，则OF=6cm，即OF等于半圆O的半径，所以AB与半圆O所在的圆相切．此时点O运动了8cm，所求运动时间为：t==4（s）‎ ‎③如图，当点O运动到BC的中点时，AC⊥OD，OC=OD=6cm，所以AC与半圆O所在的圆相切．此时点O运动了14cm，所求运动时间为：t==7（s）．‎ ‎④如图，当点O运动到B点的右侧，且OB=12cm时，过点O作OQ⊥AB，垂足为Q．在Rt△QOB中，∠OBQ=30°，则OQ=6cm，即OQ等于半圆O所在的圆的半径，‎ 所以直线AB与半圆O所在的圆相切．此时点O运动了32cm，所求运动时间为：t==16（s）．‎ ‎（2）当△ABC的一边所在的直线与半圆O所在的圆相切时，半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有如图②与③所示的两种情形．‎ ‎①如图②，设OA与半圆O的交点为M，易知重叠部分是圆心角为90°，半径为6cm的扇形，所求重叠部分面积为：S扇形EOM=π×62=9π（cm2）‎ ‎②如图③，设AB与半圆O的交点为P，连接OP，过点O作OH⊥AB，垂足为H．‎ 则PH=BH．在Rt△OBH中，∠OBH=30°，OB=6cm 则OH=3cm，BH=3cm，BP=6cm，S△POB=×6×3=9（cm2）‎ 又因为∠DOP=2∠DBP=60°‎ 所以S扇形DOP==6π（cm2）‎ 所求重叠部分面积为：S△POB+S扇形DOP=9+6π（cm2）‎