长沙市中考数学试卷及答案解析 26页

‎2018年湖南省长沙市中考数学试卷 ‎　‎ 一、选择题（在下列各题的四个选项中,只有一项是符合要求的,请在答题卡中填涂符合题意的选项,本大题共12个小题,每小题3分,共36分)‎ ‎1．（3.00分）﹣2的相反数是（　　）‎ A．﹣2 B．﹣ C．2 D．‎ ‎2．（3.00分）据统计，2017年长沙市地区生产总值约为10200亿元，经济总量迈入“万亿俱乐部”，数据10200用科学记数法表示为（　　）‎ A．0.102×105 B．10.2×103 C．1.02×104 D．1.02×103‎ ‎3．（3.00分）下列计算正确的是（　　）‎ A．a2+a3=a5 B．3 C．（x2）3=x5 D．m5÷m3=m2‎ ‎4．（3.00分）下列长度的三条线段，能组成三角形的是（　　）‎ A．4cm，5cm，9cm B．8cm，8cm，15cm C．5cm，5cm，10cm D．6cm，7cm，14cm ‎5．（3.00分）下列四个图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎6．（3.00分）不等式组的解集在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎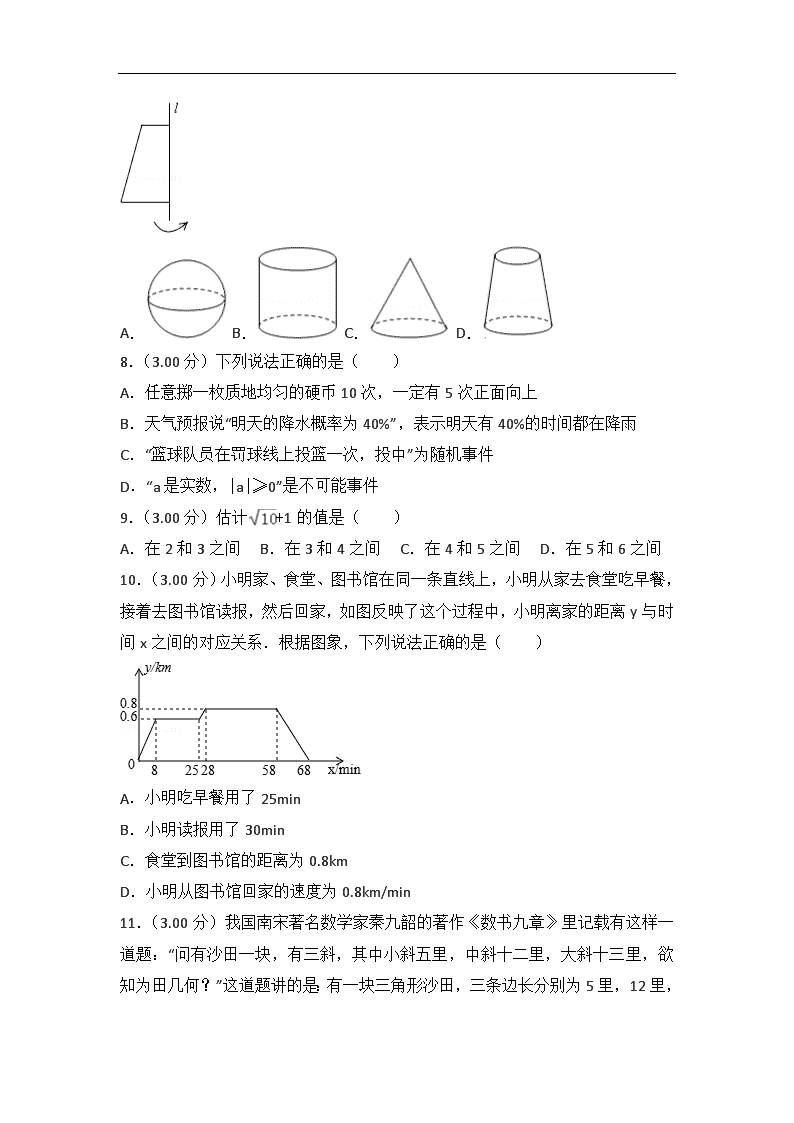7．（3.00分）将下列如图的平面图形绕轴l旋转一周，可以得到的立体图形是（　　）‎ A． B． C． D．‎ ‎8．（3.00分）下列说法正确的是（　　）‎ A．任意掷一枚质地均匀的硬币10次，一定有5次正面向上 B．天气预报说“明天的降水概率为40%”，表示明天有40%的时间都在降雨 C．“篮球队员在罚球线上投篮一次，投中”为随机事件 D．“a是实数，|a|≥0”是不可能事件 ‎9．（3.00分）估计+1的值是（　　）‎ A．在2和3之间 B．在3和4之间 C．在4和5之间 D．在5和6之间 ‎10．（3.00分）小明家、食堂、图书馆在同一条直线上，小明从家去食堂吃早餐，接着去图书馆读报，然后回家，如图反映了这个过程中，小明离家的距离y与时间x之间的对应关系．根据图象，下列说法正确的是（　　）‎ A．小明吃早餐用了25min B．小明读报用了30min C．食堂到图书馆的距离为0.8km D．小明从图书馆回家的速度为0.8km/min ‎11．（3.00分）我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（　　）‎ A．7.5平方千米 B．15平方千米 C．75平方千米 D．750平方千米 ‎12．（3.00分）若对于任意非零实数a，抛物线y=ax2+ax﹣2a总不经过点P（x0﹣3，x02﹣16），则符合条件的点P（　　）‎ A．有且只有1个 B．有且只有2个 C．有且只有3个 D．有无穷多个 ‎　‎ 二、填空题（本大题共6个小题，每小题3分，共18分)‎ ‎13．（3.00分）化简：=　 　．‎ ‎14．（3.00分）某校九年级准备开展春季研学活动，对全年级学生各自最想去的活动地点进行了调查，把调查结果制成了如下扇形统计图，则“世界之窗”对应扇形的圆心角为　 　度．‎ ‎15．（3.00分）在平面直角坐标系中，将点A′（﹣2，3）向右平移3个单位长度，再向下平移2个单位长度，那么平移后对应的点A′的坐标是　 　．‎ ‎16．（3.00分）掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，掷得面朝上的点数为偶数的概率是　 　．‎ ‎17．（3.00分）已知关于x方程x2﹣3x+a=0有一个根为1，则方程的另一个根为　 　．‎ ‎18．（3.00分）如图，点A，B，D在⊙O上，∠A=20°，BC是⊙O的切线，B为切点，OD的延长线交BC于点C，则∠OCB=　 　度．‎ ‎　‎ 三、解答题（本大题共8个小题，第19、20题每小题6分，第21、22题每小题6分，第22、23题每小题6分，第25、26题每小题6分，共66分。解答时写出必要的文字说明、证明过程或演算步骤)‎ ‎19．（6.00分）计算：（﹣1）2018﹣+（π﹣3）0+4cos45°‎ ‎20．（6.00分）先化简，再求值：（a+b）2+b（a﹣b）﹣4ab，其中a=2，b=﹣．‎ ‎21．（8.00分）为了了解居民的环保意识，社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动，并用得到的数据绘制了如图条形统计图（得分为整数，满分为10分，最低分为6分）‎ 请根据图中信息，解答下列问题：‎ ‎（1）本次调查一共抽取了　 　名居民；‎ ‎（2）求本次调查获取的样本数据的平均数、众数和中位数；‎ ‎（3）社区决定对该小区500名居民开展这项有奖问答活动，得10分者设为“一等奖”，请你根据调查结果，帮社区工作人员估计需准备多少份“一等奖”奖品？‎ ‎22．（8.00分）为加快城乡对接，建设全域美丽乡村，某地区对A、B两地间的公路进行改建．如图，A、B两地之间有一座山．汽车原来从A地到B地需途径C地沿折线ACB行驶，现开通隧道后，汽车可直接沿直线AB行驶．已知BC=80千米，∠A=45°，∠B=30°．‎ ‎（1）开通隧道前，汽车从A地到B地大约要走多少千米？‎ ‎（2）开通隧道后，汽车从A地到B地大约可以少走多少千米？（结果精确到0.1千米）（参考数据：≈141，≈1.73）‎ ‎23．（9.00分）随着中国传统节日“端午节”的临近，东方红商场决定开展“欢度端午，回馈顾客”的让利促销活动，对部分品牌粽子进行打折销售，其中甲品牌粽子打八折，乙品牌粽子打七五折，已知打折前，买6盒甲品牌粽子和3盒乙品牌粽子需600元；打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元．‎ ‎（1）打折前甲、乙两种品牌粽子每盒分别为多少元？‎ ‎（2）阳光敬老院需购买甲品牌粽子80盒，乙品牌粽子100盒，问打折后购买这批粽子比不打折节省了多少钱？‎ ‎24．（9.00分）如图，在△ABC中，AD是边BC上的中线，∠BAD=∠CAD，CE∥AD，CE交BA的延长线于点E，BC=8，AD=3．‎ ‎（1）求CE的长；‎ ‎（2）求证：△ABC为等腰三角形．‎ ‎（3）求△ABC的外接圆圆心P与内切圆圆心Q之间的距离．‎ ‎25．（10.00分）如图，在平面直角坐标系xOy中，函数y=（m为常数，m＞1，x＞0）的图象经过点P（m，1）和Q（1，m），直线PQ与x轴，y轴分别交于C，D两点，点M（x，y）是该函数图象上的一个动点，过点M分别作x轴和y轴的垂线，垂足分别为A，B．‎ ‎（1）求∠OCD的度数；‎ ‎（2）当m=3，1＜x＜3时，存在点M使得△OPM∽△OCP，求此时点M的坐标；‎ ‎（3）当m=5时，矩形OAMB与△OPQ的重叠部分的面积能否等于4.1？请说明你的理由．‎ ‎26．（10.00分）我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”．‎ ‎（1）①在“平行四边形，矩形，菱形，正方形”中，一定是“十字形”的有　 　；‎ ‎②在凸四边形ABCD中，AB=AD且CB≠CD，则该四边形　 　“十字形”．（填“是”或“不是”）‎ ‎（2）如图1，A，B，C，D是半径为1的⊙O上按逆时针方向排列的四个动点，AC与BD交于点E，∠ADB﹣∠CDB=∠ABD﹣∠CBD，当6≤AC2+BD2≤7时，求OE的取值范围；‎ ‎（3）如图2，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a，b，c为常数，a＞0，c＜0）与x轴交于A，C两点（点A在点C的左侧），B是抛物线与y轴的交点，点D的坐标为（0，﹣ac），记“十字形”ABCD的面积为S，记△AOB，△COD，△AOD，△BOC的面积分别为S1，S2，S3，S4．求同时满足下列三个条件的抛物线的解析式；‎ ‎①=；②=；③“十字形”ABCD的周长为12．‎ ‎　‎ ‎2018年湖南省长沙市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（在下列各题的四个选项中,只有一项是符合要求的,请在答题卡中填涂符合题意的选项,本大题共12个小题,每小题3分,共36分)‎ ‎1．（3.00分）﹣2的相反数是（　　）‎ A．﹣2 B．﹣ C．2 D．‎ ‎【分析】根据只有符号不同的两个数互为相反数，可得答案．‎ ‎【解答】解：﹣2的相反数是2，‎ 故选：C．‎ ‎　‎ ‎2．（3.00分）据统计，2017年长沙市地区生产总值约为10200亿元，经济总量迈入“万亿俱乐部”，数据10200用科学记数法表示为（　　）‎ A．0.102×105 B．10.2×103 C．1.02×104 D．1.02×103‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．‎ ‎【解答】解：10200=1.02×104，‎ 故选：C．‎ ‎　‎ ‎3．（3.00分）下列计算正确的是（　　）‎ A．a2+a3=a5 B．3 C．（x2）3=x5 D．m5÷m3=m2‎ ‎【分析】直接利用合并同类项法则以及幂的乘方运算法则、同底数幂的乘除运算法则分别计算得出答案．‎ ‎【解答】解：A、a2+a3，无法计算，故此选项错误；‎ B、3﹣2=，故此选项错误；‎ C、（x2）3=x6，故此选项错误；‎ D、m5÷m3=m2，正确．‎ 故选：D．‎ ‎　‎ ‎4．（3.00分）下列长度的三条线段，能组成三角形的是（　　）‎ A．4cm，5cm，9cm B．8cm，8cm，15cm C．5cm，5cm，10cm D．6cm，7cm，14cm ‎【分析】结合“三角形中较短的两边之和大于第三边”，分别套入四个选项中得三边长，即可得出结论．‎ ‎【解答】解：A、∵5+4=9，9=9，‎ ‎∴该三边不能组成三角形，故此选项错误；‎ B、8+8=16，16＞15，‎ ‎∴该三边能组成三角形，故此选项正确；‎ C、5+5=10，10=10，‎ ‎∴该三边不能组成三角形，故此选项错误；‎ D、6+7=13，13＜14，‎ ‎∴该三边不能组成三角形，故此选项错误；‎ 故选：B．‎ ‎　‎ ‎5．（3.00分）下列四个图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎【分析】根据轴对称图形与中心对称图形的概念求解．‎ ‎【解答】解：A、是轴对称图形，是中心对称图形，故此选项正确；‎ B、是轴对称图形，不是中心对称图形，故此选项错误；‎ C、不是轴对称图形，不是中心对称图形，故此选项错误；‎ D、不是轴对称图形，是中心对称图形，故此选项错误；‎ 故选：A．‎ ‎　‎ ‎6．（3.00分）不等式组的解集在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎【分析】先求出各不等式的解集，再求出其公共解集即可．‎ ‎【解答】解：解不等式x+2＞0，得：x＞﹣2，‎ 解不等式2x﹣4≤0，得：x≤2，‎ 则不等式组的解集为﹣2＜x≤2，‎ 将解集表示在数轴上如下：‎ 故选：C．‎ ‎　‎ ‎7．（3.00分）将下列如图的平面图形绕轴l旋转一周，可以得到的立体图形是（　　）‎ A． B． C． D．‎ ‎【分析】根据面动成体以及圆台的特点进行逐一分析，能求出结果．‎ ‎【解答】解：绕直线l旋转一周，可以得到圆台，‎ 故选：D．‎ ‎　‎ ‎8．（3.00分）下列说法正确的是（　　）‎ A．任意掷一枚质地均匀的硬币10次，一定有5次正面向上 B．天气预报说“明天的降水概率为40%”，表示明天有40%的时间都在降雨 C．“篮球队员在罚球线上投篮一次，投中”为随机事件 D．“a是实数，|a|≥0”是不可能事件 ‎【分析】直接利用概率的意义以及随机事件的定义分别分析得出答案．‎ ‎【解答】解：A、任意掷一枚质地均匀的硬币10次，一定有5次正面向上，错误；‎ B、天气预报说“明天的降水概率为40%”，表示明天有40%的时间都在降雨，错误；‎ C、“篮球队员在罚球线上投篮一次，投中”为随机事件，正确；‎ D、“a是实数，|a|≥0”是必然事件，故此选项错误．‎ 故选：C．‎ ‎　‎ ‎9．（3.00分）估计+1的值是（　　）‎ A．在2和3之间 B．在3和4之间 C．在4和5之间 D．在5和6之间 ‎【分析】应先找到所求的无理数在哪两个和它接近的整数之间，然后判断出所求的无理数的范围．‎ ‎【解答】解：∵32=9，42=16，‎ ‎∴，‎ ‎∴+1在4到5之间．‎ 故选：C．‎ ‎　‎ ‎10．（3.00分）小明家、食堂、图书馆在同一条直线上，小明从家去食堂吃早餐，接着去图书馆读报，然后回家，如图反映了这个过程中，小明离家的距离y与时间x之间的对应关系．根据图象，下列说法正确的是（　　）‎ A．小明吃早餐用了25min B．小明读报用了30min C．食堂到图书馆的距离为0.8km D．小明从图书馆回家的速度为0.8km/min ‎【分析】根据函数图象判断即可．‎ ‎【解答】解：小明吃早餐用了（25﹣8）=17min，A错误；‎ 小明读报用了（58﹣28）=30min，B正确；‎ 食堂到图书馆的距离为（0.8﹣0.6）=0.2km，C错误；‎ 小明从图书馆回家的速度为0.8÷10=0.08km/min，D错误；‎ 故选：B．‎ ‎　‎ ‎11．（3.00分）我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（　　）‎ A．7.5平方千米 B．15平方千米 C．75平方千米 D．750平方千米 ‎【分析】直接利用勾股定理的逆定理进而结合直角三角形面积求法得出答案．‎ ‎【解答】解：∵52+122=132，‎ ‎∴三条边长分别为5里，12里，13里，构成了直角三角形，‎ ‎∴这块沙田面积为：×5×500×12×500=7500000（平方米）=7.5（平方千米）．‎ 故选：A．‎ ‎　‎ ‎12．（3.00分）若对于任意非零实数a，抛物线y=ax2+ax﹣2a总不经过点P（x0﹣3，x02﹣16），则符合条件的点P（　　）‎ A．有且只有1个 B．有且只有2个 C．有且只有3个 D．有无穷多个 ‎【分析】根据题意可以得到相应的不等式，然后根据对于任意非零实数a，抛物线y=ax2+ax﹣2a总不经过点P（x0﹣3，x02﹣16），即可求得点P的坐标，从而可以解答本题．‎ ‎【解答】解：∵对于任意非零实数a，抛物线y=ax2+ax﹣2a总不经过点P（x0﹣3，x02﹣16），‎ ‎∴x02﹣16≠a（x0﹣3）2+a（x0﹣3）﹣2a ‎∴（x0﹣4）（x0+4）≠a（x0﹣1）（x0﹣4）‎ ‎∴（x0+4）≠a（x0﹣1）‎ ‎∴x0=﹣4或x0=1，‎ ‎∴点P的坐标为（﹣7，0）或（﹣2，﹣15）‎ 故选：B．‎ ‎　‎ 二、填空题（本大题共6个小题，每小题3分，共18分)‎ ‎13．（3.00分）化简：=　1　．‎ ‎【分析】根据分式的加减法法则：同分母分式加减法法则：同分母的分式想加减，分母不变，把分子相加减计算即可．‎ ‎【解答】解：原式==1．‎ 故答案为：1．‎ ‎　‎ ‎14．（3.00分）某校九年级准备开展春季研学活动，对全年级学生各自最想去的活动地点进行了调查，把调查结果制成了如下扇形统计图，则“世界之窗”对应扇形的圆心角为　90　度．‎ ‎【分析】根据圆心角=360°×百分比计算即可；‎ ‎【解答】解：“世界之窗”对应扇形的圆心角=360°×（1﹣10%﹣30%﹣20%﹣15%）=90°，‎ 故答案为90．‎ ‎　‎ ‎15．（3.00分）在平面直角坐标系中，将点A′（﹣2，3）向右平移3个单位长度，再向下平移2个单位长度，那么平移后对应的点A′的坐标是　（1，1）　．‎ ‎【分析】直接利用平移的性质分别得出平移后点的坐标得出答案．‎ ‎【解答】解：∵将点A′（﹣2，3）向右平移3个单位长度，‎ ‎∴得到（1，3），‎ ‎∵再向下平移2个单位长度，‎ ‎∴平移后对应的点A′的坐标是：（1，1）．‎ 故答案为：（1，1）．‎ ‎　‎ ‎16．（3.00分）掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，掷得面朝上的点数为偶数的概率是　　．‎ ‎【分析】先统计出偶数点的个数，再根据概率公式解答．‎ ‎【解答】解：正方体骰子共六个面，点数为1，2，3，4，5，6，偶数为2，4，6，‎ 故点数为偶数的概率为=，‎ 故答案为：．‎ ‎　‎ ‎17．（3.00分）已知关于x方程x2﹣3x+a=0有一个根为1，则方程的另一个根为　2　．‎ ‎【分析】设方程的另一个根为m，根据两根之和等于﹣，即可得出关于m的一元一次方程，解之即可得出结论．‎ ‎【解答】解：设方程的另一个根为m，‎ 根据题意得：1+m=3，‎ 解得：m=2．‎ 故答案为：2．‎ ‎　‎ ‎18．（3.00分）如图，点A，B，D在⊙O上，∠A=20°，BC是⊙O的切线，B为切点，OD的延长线交BC于点C，则∠OCB=　50　度．‎ ‎【分析】由圆周角定理易求∠BOC的度数，再根据切线的性质定理可得∠OBC=90°，进而可求出求出∠OCB的度°°‎ ‎【解答】解：‎ ‎∵∠A=20°，‎ ‎∴∠BOC=40°，‎ ‎∵BC是⊙O的切线，B为切点，‎ ‎∴∠OBC=90°，‎ ‎∴∠OCB=90°﹣40°=50°，‎ 故答案为：50．‎ ‎　‎ 三、解答题（本大题共8个小题，第19、20题每小题6分，第21、22题每小题6分，第22、23题每小题6分，第25、26题每小题6分，共66分。解答时写出必要的文字说明、证明过程或演算步骤)‎ ‎19．（6.00分）计算：（﹣1）2018﹣+（π﹣3）0+4cos45°‎ ‎【分析】本题涉及零指数幂、乘方、二次根式化简和特殊角的三角函数值4个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．‎ ‎【解答】解：原式=1﹣2+1+4×=1﹣2+1+2=2．‎ ‎　‎ ‎20．（6.00分）先化简，再求值：（a+b）2+b（a﹣b）﹣4ab，其中a=2，b=﹣．‎ ‎【分析】首先计算完全平方，计算单项式乘以多项式，然后再合并同类项，化简后，再代入a、b的值，进而可得答案．‎ ‎【解答】解：原式=a2+2ab+b2+ab﹣b2﹣4ab=a2﹣ab，‎ 当a=2，b=﹣时，原式=4+1=5．‎ ‎　‎ ‎21．（8.00分）为了了解居民的环保意识，社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动，并用得到的数据绘制了如图条形统计图（得分为整数，满分为10分，最低分为6分）‎ 请根据图中信息，解答下列问题：‎ ‎（1）本次调查一共抽取了　50　名居民；‎ ‎（2）求本次调查获取的样本数据的平均数、众数和中位数；‎ ‎（3）社区决定对该小区500名居民开展这项有奖问答活动，得10分者设为“一等奖”，请你根据调查结果，帮社区工作人员估计需准备多少份“一等奖”奖品？‎ ‎【分析】（1）根据总数=个体数量之和计算即可；‎ ‎（2）根据平均数、总数、中位数的定义计算即可；‎ ‎（3）利用样本估计总体的思想解决问题即可；‎ ‎【解答】解：（1）共抽取：4+10+15+11+10=50（人），‎ 故答案为50；‎ ‎（2）平均数=（4×6+10×7+15×8=11×9+10×10）=8.26；‎ 众数：得到8分的人最多，故众数为8．‎ 中位数：由小到大排列，知第25，26平均分为8分，故中位数为8分；‎ ‎（3）得到10分占10÷50=20%，‎ 故500人时，需要一等奖奖品500×20%=100（份）．‎ ‎　‎ ‎22．（8.00分）为加快城乡对接，建设全域美丽乡村，某地区对A、B两地间的公路进行改建．如图，A、B两地之间有一座山．汽车原来从A地到B地需途径C地沿折线ACB行驶，现开通隧道后，汽车可直接沿直线AB行驶．已知BC=80千米，∠A=45°，∠B=30°．‎ ‎（1）开通隧道前，汽车从A地到B地大约要走多少千米？‎ ‎（2）开通隧道后，汽车从A地到B地大约可以少走多少千米？（结果精确到0.1千米）（参考数据：≈141，≈1.73）‎ ‎【分析】（1）过点C作AB的垂线CD，垂足为D，在直角△ACD中，解直角三角形求出CD，进而解答即可；‎ ‎（2）在直角△CBD中，解直角三角形求出BD，再求出AD，进而求出汽车从A地到B地比原来少走多少路程．‎ ‎【解答】解：（1）过点C作AB的垂线CD，垂足为D，‎ ‎∵AB⊥CD，sin30°=，BC=80千米，‎ ‎∴CD=BC•sin30°=80×（千米），‎ AC=（千米），‎ AC+BC=80+40≈40×1.41+80=136.4（千米），‎ 答：开通隧道前，汽车从A地到B地大约要走136.4千米；‎ ‎（2）∵cos30°=，BC=80（千米），‎ ‎∴BD=BC•cos30°=80×（千米），‎ ‎∵tan45°=，CD=40（千米），‎ ‎∴AD=（千米），‎ ‎∴AB=AD+BD=40+40≈40+40×1.73=109.2（千米），‎ ‎∴汽车从A地到B地比原来少走多少路程为：AC+BC﹣AB=136.4﹣109.2=27.2（千米）．‎ 答：汽车从A地到B地比原来少走的路程为27.2千米．‎ ‎　‎ ‎23．（9.00分）随着中国传统节日“端午节”的临近，东方红商场决定开展“欢度端午，回馈顾客”的让利促销活动，对部分品牌粽子进行打折销售，其中甲品牌粽子打八折，乙品牌粽子打七五折，已知打折前，买6盒甲品牌粽子和3盒乙品牌粽子需600元；打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元．‎ ‎（1）打折前甲、乙两种品牌粽子每盒分别为多少元？‎ ‎（2）阳光敬老院需购买甲品牌粽子80盒，乙品牌粽子100盒，问打折后购买这批粽子比不打折节省了多少钱？‎ ‎【分析】（1）设打折前甲品牌粽子每盒x元，乙品牌粽子每盒y元，根据“打折前，买6盒甲品牌粽子和3盒乙品牌粽子需600元；打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元”，即可得出关于x、y的二元一次方程组，解之即可得出结论；‎ ‎（2）根据节省钱数=原价购买所需钱数﹣打折后购买所需钱数，即可求出节省的钱数．‎ ‎【解答】解：（1）设打折前甲品牌粽子每盒x元，乙品牌粽子每盒y元，‎ 根据题意得：，‎ 解得：．‎ 答：打折前甲品牌粽子每盒40元，乙品牌粽子每盒120元．‎ ‎（2）80×40+100×120﹣80×0.8×40﹣100×0.75×120=3640（元）．‎ 答：打折后购买这批粽子比不打折节省了3640元．‎ ‎　‎ ‎24．（9.00分）如图，在△ABC中，AD是边BC上的中线，∠BAD=∠CAD，CE∥AD，CE交BA的延长线于点E，BC=8，AD=3．‎ ‎（1）求CE的长；‎ ‎（2）求证：△ABC为等腰三角形．‎ ‎（3）求△ABC的外接圆圆心P与内切圆圆心Q之间的距离．‎ ‎【分析】（1）证明AD为△BCE的中位线得到CE=2AD=6；‎ ‎（2）通过证明△ABD≌△CAD得到AB=AC；‎ ‎（3）如图，连接BP、BQ、CQ，先利用勾股定理计算出AB=5，设⊙P的半径为R，⊙Q的半径为r，在Rt△PBD中利用勾股定理得到（R﹣3）2+42=R2，解得R=，则PD=，再利用面积法求出r=，即QD=，然后计算PD+QD即可．‎ ‎【解答】（1）解：∵AD是边BC上的中线，‎ ‎∴BD=CD，‎ ‎∵CE∥AD，‎ ‎∴AD为△BCE的中位线，‎ ‎∴CE=2AD=6；‎ ‎（2）证明：∵BD=CD，∠BAD=∠CAD，AD=AD，‎ ‎∴△ABD≌△CAD，‎ ‎∴AB=AC，‎ ‎∴△ABC为等腰三角形．‎ ‎（3）如图，连接BP、BQ、CQ，‎ 在Rt△ABD中，AB==5，‎ 设⊙P的半径为R，⊙Q的半径为r，‎ 在Rt△PBD中，（R﹣3）2+42=R2，解得R=，‎ ‎∴PD=PA﹣AD=﹣3=，‎ ‎∵S△ABQ+S△BCQ+S△ACQ=S△ABC，‎ ‎∴•r•5+•r•8+•r•5=•3•8，解得r=，‎ 即QD=，‎ ‎∴PQ=PD+QD=+=．‎ 答：△ABC的外接圆圆心P与内切圆圆心Q之间的距离为．‎ ‎　‎ ‎25．（10.00分）如图，在平面直角坐标系xOy中，函数y=（m为常数，m＞1，x＞0）的图象经过点P（m，1）和Q（1，m），直线PQ与x轴，y轴分别交于C，D两点，点M（x，y）是该函数图象上的一个动点，过点M分别作x轴和y轴的垂线，垂足分别为A，B．‎ ‎（1）求∠OCD的度数；‎ ‎（2）当m=3，1＜x＜3时，存在点M使得△OPM∽△OCP，求此时点M的坐标；‎ ‎（3）当m=5时，矩形OAMB与△OPQ的重叠部分的面积能否等于4.1？请说明你的理由．‎ ‎【分析】（1）想办法证明OC=OD即可解决问题；‎ ‎（2）设M（a，），由△OPM∽△OCP，推出==，由此构建方程求出a，再分类求解即可解决问题；‎ ‎（3）不存在分三种情形说明：①当1＜x＜5时，如图1中；②当x≤1时，如图2中；③当x≥5时，如图3中；‎ ‎【解答】解：（1）设直线PQ的解析式为y=kx+b，则有，‎ 解得，‎ ‎∴y=﹣x+m+!，‎ 令x=0，得到y=m+1，∴D（0，m+1），‎ 令y+0，得到x=m+1，∴C（m+1，0），‎ ‎∴OC=OD，‎ ‎∵∠COD=90°，‎ ‎∴∠OCD=45°．‎ ‎（2）设M（a，），‎ ‎∵△OPM∽△OCP，‎ ‎∴==，‎ ‎∴OP2=OC•OM，‎ 当m=3时，P（3，1），C（4，0），‎ OP2=32+12=10，OC=4，OM=，‎ ‎∴=，‎ ‎∴10=4，‎ ‎∴4a4﹣25a2+36=0，‎ ‎（4a2﹣9）（a2﹣4）=0，‎ ‎∴a=±，a=±2，‎ ‎∵1＜a＜3，‎ ‎∴a=或2，‎ 当a=时，M（，2），‎ PM=，CP=，‎ ‎≠（舍弃），‎ 当a=2时，M（2，），PM=，CP=，‎ ‎∴==，成立，‎ ‎∴M（2，）．‎ ‎（3）不存在．理由如下：‎ 当m=5时，P（5，1），Q（1，5），设M（x，），‎ OP的解析式为：y=x，OQ的解析式为y=5x，‎ ‎①当1＜x＜5时，如图1中，‎ ‎∴E（，），F（x，x），‎ S=S矩形OAMB﹣S△OAF﹣S△OBE ‎=5﹣•x•x﹣••=4.1，‎ 化简得到：x4﹣9x2+25=0，‎ ‎△＜O，‎ ‎∴没有实数根．‎ ‎②当x≤1时，如图2中，‎ S=S△OGH＜S△OAM=2.5，‎ ‎∴不存在，‎ ‎③当x≥5时，如图3中，‎ S=S△OTS＜S△OBM=2.5，‎ ‎∴不存在，‎ 综上所述，不存在．‎ ‎　‎ ‎26．（10.00分）我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”．‎ ‎（1）①在“平行四边形，矩形，菱形，正方形”中，一定是“十字形”的有　菱形，正方形　；‎ ‎②在凸四边形ABCD中，AB=AD且CB≠CD，则该四边形　不是　“十字形”．（填“是”或“不是”）‎ ‎（2）如图1，A，B，C，D是半径为1的⊙O上按逆时针方向排列的四个动点，AC与BD交于点E，∠ADB﹣∠CDB=∠ABD﹣∠CBD，当6≤AC2+BD2≤7时，求OE的取值范围；‎ ‎（3）如图2，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a，b，c为常数，a＞0，c＜0）与x轴交于A，C两点（点A在点C的左侧），B是抛物线与y轴的交点，点D的坐标为（0，﹣ac），记“十字形”ABCD的面积为S，记△AOB，△COD，△AOD，△BOC的面积分别为S1，S2，S3，S4．求同时满足下列三个条件的抛物线的解析式；‎ ‎①=；②=；③“十字形”ABCD的周长为12．‎ ‎【分析】（1）利用“十字形”的定义判断即可；‎ ‎（2）先判断出∠ADB+∠CAD=∠ABD+∠CAB，进而判断出∠AED=∠AEB=90°，即：AC⊥BD，再判断出四边形OMEN是矩形，进而得出OE2=2﹣（AC2+BD2），即可得出结论；‎ ‎（3）由题意得，A（，0），B（0，c），C（‎ ‎，0），D（0，﹣ac），求出S=AC•BD=﹣（ac+c）×，S1=OA•OB=﹣，S2=OC•OD=﹣，S3=OA×OD=﹣，S4=OB×OC=﹣，进而建立方程+=+，求出a=1，再求出b=0，进而判断出四边形ABCD是菱形，求出AD=3，进而求出c=﹣9，即可得出结论．‎ ‎【解答】解：（1）①∵菱形，正方形的对角线互相垂直，‎ ‎∴菱形，正方形是：“十字形”，‎ ‎∵平行四边形，矩形的对角线不一定垂直，‎ ‎∴平行四边形，矩形不是“十字形”，‎ 故答案为：菱形，正方形；‎ ‎②如图，‎ 当CB=CD时，在△ABC和△ADC中，，‎ ‎∴△ABC≌△ADC（SSS），‎ ‎∴∠BAC=∠DAC，‎ ‎∵AB=AD，‎ ‎∴AC⊥BD，‎ ‎∴当CB≠CD时，四边形ABCD不是“十字形”，‎ 故答案为：不是；‎ ‎（2）∵∠ADB+∠CBD=∠ABD+∠CDB，∠CBD=∠CDB=∠CAB，‎ ‎∴∠ADB+∠CAD=∠ABD+∠CAB，‎ ‎∴180°﹣∠AED=180°﹣∠AEB，‎ ‎∴∠AED=∠AEB=90°，‎ ‎∴AC⊥BD，‎ 过点O作OM⊥AC于M，ON⊥BD于N，连接OA，OD，‎ ‎∴OA=OD=1，OM2=OA2﹣AM2，ON2=OD2﹣DN2，AM=AC，DN=‎ BD，四边形OMEN是矩形，‎ ‎∴ON=ME，OE2=OM2+ME2，‎ ‎∴OE2=OM2+ON2=2﹣（AC2+BD2），‎ ‎∵6≤AC2+BD2≤7，‎ ‎∴2﹣≤OE2≤2﹣，‎ ‎∴≤OE2≤，‎ ‎∴（OE＞0）；‎ ‎（3）由题意得，A（，0），B（0，c），C（，0），D（0，﹣ac），‎ ‎∵a＞0，c＜0，‎ ‎∴OA=，OB=﹣c，OC=，OD=﹣ac，AC=，BD=﹣ac﹣c，‎ ‎∴S=AC•BD=﹣（ac+c）×，S1=OA•OB=﹣，S2=OC•OD=﹣，‎ S3=OA×OD=﹣，S4=OB×OC=﹣，‎ ‎∵=+，=+，‎ ‎∴+=+，‎ ‎∴=2，‎ ‎∴a=1，‎ ‎∴S=﹣c，S1=﹣，S4=﹣，‎ ‎∵，‎ ‎∴S=S1+S2+2，‎ ‎∴﹣c=﹣+2，‎ ‎∴﹣=﹣c•，‎ ‎∴=，‎ ‎∴b=0，‎ ‎∴A（﹣，0），B（0，c），C（，0），d（0，﹣c），‎ ‎∴四边形ABCD是菱形，‎ ‎∴4AD=12，‎ ‎∴AD=3，‎ 即：AD2=90，‎ ‎∵AD2=c2﹣c，‎ ‎∴c2﹣c=90，‎ ‎∴c=﹣9或c=10（舍），‎ 即：y=x2﹣9．‎ ‎　‎