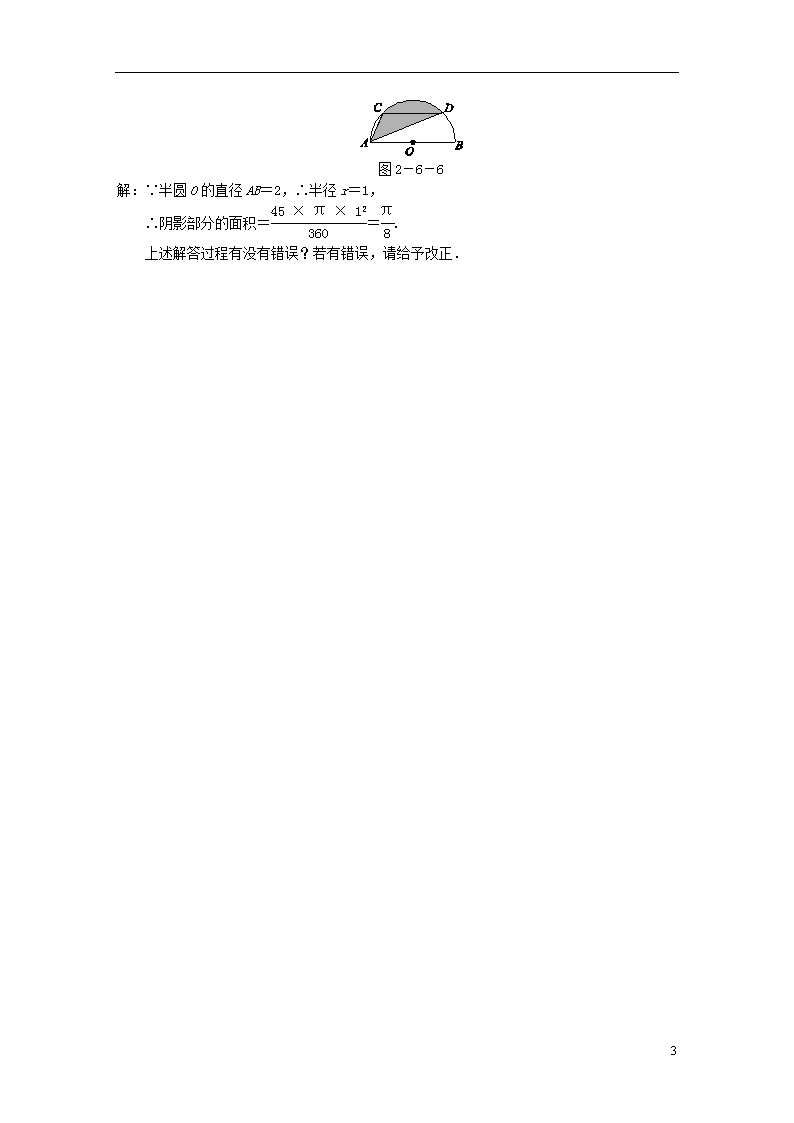2020九年级数学下册 第2章 弧长与扇形面积 4页

‎2.6　弧长与扇形面积 ‎ 第2课时　扇形的面积公式 知|识|目|标 ‎1．经历探索n°的圆心角所对的弧长和扇形面积的过程，推导出扇形面积公式，并应用公式解决相关问题．‎ ‎2．通过掌握扇形的面积公式，能求弓形等组合图形的面积.‎ 目标一　理解扇形面积公式并能解决相关问题 例1 教材例3针对训练(1)已知扇形的圆心角为120°，半径为2 cm，则扇形的面积是________cm2；‎ ‎(2)已知扇形的半径为‎2 cm，面积是π cm2，则扇形圆心角的度数为________度；‎ ‎(3)已知扇形的弧长是10π cm，面积为20π cm2，则扇形的半径为________．‎ ‎【归纳总结】扇形面积公式的选择：‎ ‎(1)当已知半径R和圆心角的度数求扇形的面积时，选用公式S＝；‎ ‎(2)当已知半径R和弧长l求扇形的面积时，选用公式S＝lR.‎ 目标二　能求弓形等组合图形的面积 例2 教材补充例题如图2－6－3，已知扇形的圆心角为60°，半径为，则图中弓形的面积为(　　)‎ 图2－6－3‎ 4‎ A.　　B. ‎ C.　　D. ‎ ‎【归纳总结】两类弓形面积的求法：‎ ‎(1)小于半圆的弧与弦组成的弓形，如图2－6－4①，用扇形的面积减去三角形的面积即为弓形面积；‎ 图2－6－4‎ ‎(2)大于半圆的弧与弦组成的弓形，如图2－6－4②，用扇形的面积加上三角形的面积即为弓形面积．‎ 例3 教材补充例题如图2－6－5，半圆O的直径AB＝2，弦CD∥AB，∠CAD＝30°，求阴影部分的面积(结果保留π)．‎ 图2－6－5‎ ‎【归纳总结】组合图形的面积的化归方法：‎ ‎(1)化归为弓形的面积与三角形面积的和与差；‎ ‎(2)利用对称性将图形转移位置，形成扇形、三角形、特殊四边形或弓形进行计算．‎ 知识点　扇形面积公式 ‎1．圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形．在同一个圆中，圆心角越大，扇形的面积就越大．‎ ‎2．半径为r的圆中，圆心角为n°的扇形的面积S＝________．若扇形的弧长为l，则S＝________．‎ ‎[说明] 扇形面积公式要根据具体的情况来使用，当已知圆心角和半径时，通常使用S扇形＝；当已知弧长和半径或弧长和圆心角时，通常使用S扇形＝lr.‎ ‎[注意] 1.公式中n表示圆心角的度数，且代入计算时不带单位．‎ ‎2．计算结果无精确度要求时，结果保留π.‎ 如图2－6－6，半圆O的直径AB＝2，弦CD∥AB，∠CAD＝45°，求图中阴影部分的面积．‎ 4‎ 图2－6－6‎ 解：∵半圆O的直径AB＝2，∴半径r＝1，‎ ‎∴阴影部分的面积＝＝.‎ 上述解答过程有没有错误？若有错误，请给予改正．‎ 4‎ 教师详解详析 ‎【目标突破】‎ 例1　(1)π 　(2)90　(3)4 cm 例2　C 例3　解：连接OC，OD，如图．∵∠CAD＝30°，‎ ‎∴∠COD＝60°.‎ ‎∵AB∥CD，‎ ‎∴S△ACD＝S△COD，∴S阴影＝S弓形CD＋S△COD＝S扇形OCD＝＝π.‎ ‎【总结反思】‎ ‎[小结] 知识点　　lr ‎[反思] ‎ 上述解答有错误，∠CAD＝45°是圆周角的度数，要转化为圆心角的度数．正确解答：连接OC，OD.由CD∥AB可知，点A，O到直线CD的距离相等，∴S△ACD＝S△OCD，而∠COD＝2∠CAD＝90°，∴S阴影＝S扇形OCD＝×π×＝.‎ 4‎