2019年安徽省合肥市蜀山区中考数学一模试卷 24页

‎2019年安徽省合肥市蜀山区中考数学一模试卷 一、选择题（本大题共10小题，每小题4分.每小题都给出A、B、C、D四个选项，其中只有一个是正确的.）‎ ‎1．（4分）的倒数是　　‎ A．3 B． C． D．‎ ‎2．（4分）计算所得结果是　　‎ A． B． C． D．‎ ‎3．（4分）某手机芯片采用16纳米工艺纳米米），其中16纳米用科学记数法表示为　　‎ A．米 B．米 C． D．米[来源:学科网]‎ ‎4．（4分）如图是一个几何体的三视图，根据图中所示数据求得这个几何体的侧面面积是　　‎ A． B． C． D．‎ ‎5．（4分）如图，在中，，平分，交于，，交于，则的大小是　　‎ A． B． C． D．‎ ‎6．（4分）合肥市统计局资料显示，2016年全市生产总值为6274.3亿元，2018年全市生产总值为7822.9亿元，假设2017年，假如2017年与2018年这两年的年平均增长率均为，则下列方程式正确的是　　‎ A． ‎ B． ‎ C． ‎ D． ‎ ‎7．（4分）为了响应学校“皖疆手拉手，书香飘校园”的爱心捐书活动，励志班的同学们积极捐书，其中该班雄鹰小组的同学们捐书册数分别是：5，7，，3，4，6．已知他们平均每人捐5本，则这组数据的众数、中位数和方差分别是　　‎ A．5，5.5，10 B．5，5， C．5，5， D．6，5.5，‎ ‎8．（4分）已知关于的一元二次方程有两个不相等的实数根，则实数的取值范围是　　‎ A． B． C． D．‎ ‎9．（4分）如图，，、相交于点，过点的直线分别交、于点、，则下列结论不一定成立的是　　‎ A． B． C． D．‎ ‎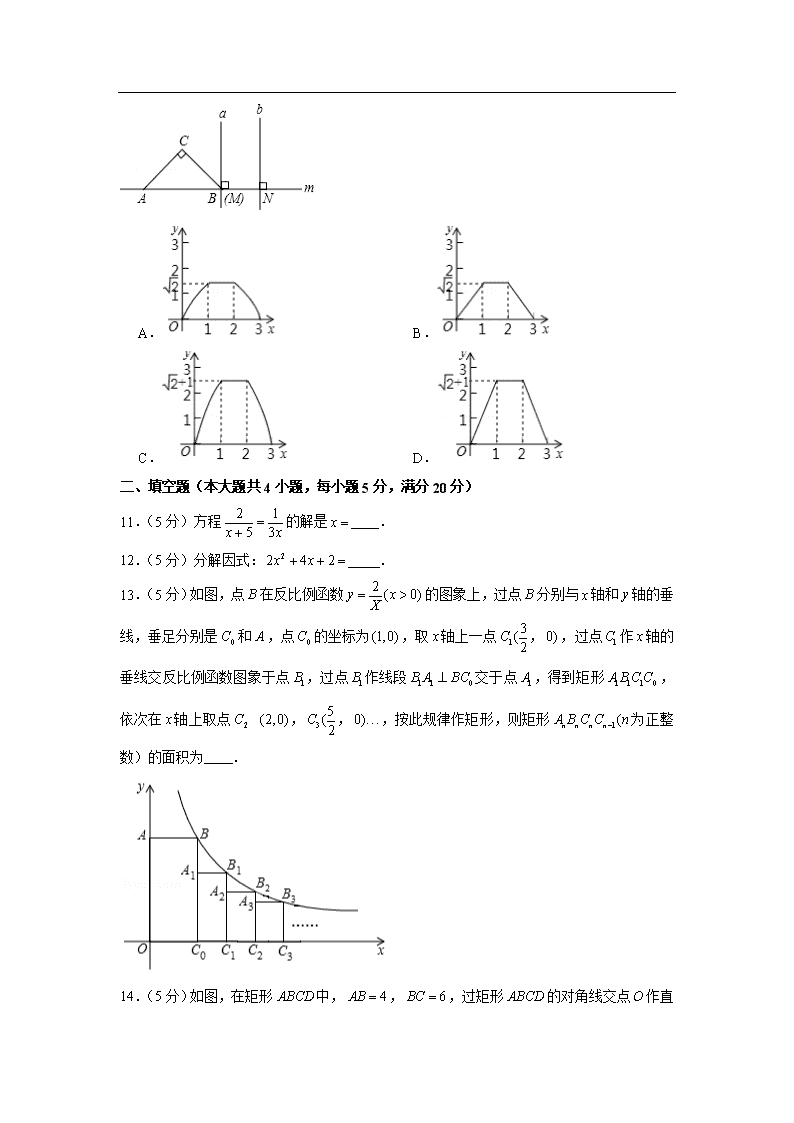10．（4分）如图直线，都与直线垂直，垂足分别为、，，等腰直角的斜边，在直线上，，且点位于点处，将等腰直角沿直线向右平移，直到点与点重合为止，记点平移平移的距离为，等腰直角的边位于直线，之间部分的长度和为，则关于的函数图象大致为　　‎ A． B． ‎ C． D．‎ 二、填空题（本大题共4小题，每小题5分，满分20分）‎ ‎11．（5分）方程的解是　　．‎ ‎12．（5分）分解因式：　 　．‎ ‎13．（5分）如图，点在反比例函数的图象上，过点分别与轴和轴的垂线，垂足分别是和，点的坐标为，取轴上一点，，过点作轴的垂线交反比例函数图象于点，过点作线段交于点，得到矩形，依次在轴上取点 ，，，按此规律作矩形，则矩形为正整数）的面积为　　．‎ ‎14．（5分）如图，在矩形中，，，过矩形的对角线交点 作直线分别交、于点、，连接，若是等腰三角形，则　　．‎ 三、（本大题共2小题，每小题8分，满分16分）‎ ‎15．（8分）计算：‎ ‎16．（8分）先化简，再求值：，其中．‎ 四、（本大题共2小题，每小题8分，满分16分）‎ ‎17．（8分）如图，在由边长为1个单位长度的小正方形组成的网格中，，，．‎ ‎（1）将先向下平移3个单位长度，再向左平移2个单位长度，作出平移后的△．‎ ‎（2）将△绕点逆时针旋转，作出旋转后的△．‎ ‎（3）在（2）的旋转过程中，点经过的路径长为　　．‎ ‎18．（8分）《九章算术》中有这样一道题，原文如下：‎ 今有甲乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而钱亦五十．问甲、乙持钱各几何？‎ 大意为：‎ 今有甲、乙二人，不知其钱包里有多少钱，若乙把其一半的钱给甲，则甲的钱数为50；若甲把其的钱给乙，问甲、乙各有多少钱？‎ 请解答上述问题．‎ 五、（本大题共2小题，每小题10分，满分20分）‎ ‎19．（10分）如图，、、三地在同一直线上，在的北偏东方向，在的北偏西方向，在的北偏西方向，且，求与之间的距离．‎ ‎20．（10分）如图，已知四边形的外接圆的半径为4，弦与的交点为，与相交于点，．‎ ‎（1）求证：；‎ ‎（2）若，，求的面积．‎ 六、（本题满分12分）‎ ‎21．（12分）随着智能手机的普及率越来越高以及移动支付的快捷高效性，中国移动支付在世界处于领先水平，为了解人们平时最喜欢用哪种移动支付方式，因此在某步行街对行人进行随机抽样调查，以下是根据调查结果分别整理的不完整的统计表和统计图．‎ 移动支付方式 支付宝 微信 其他 人数人 ‎200[来源:学,科,网Z,X,X,K]‎ ‎75‎ 请你根据上述统计表和统计图提供的信息．完成下列问题 ‎（1）在此次调查中，使用支付宝支付的人数为　　人，表示微信支付的扇形所对的圆心角度数为　　度．‎ ‎（2）某天该步行街人流量为10万人，其中的人购物并选择移动支付，请你依据此次调查获得的信息估计一下当天使用微信支付的人数．‎ ‎（3‎ ‎）甲、乙、丙三人都只习惯使用支付宝和微信支付，并且他们选择这两种支付的可能性是相同的，请计算三人恰好选择同一种支付方式的概率．‎ 七、（本题满分12分）‎ ‎22．（12分）小明大学毕业后积极响应政府号召回乡创业，准备经营水果生意，他在批发市场了解到某种水果的批发单价与批发量有如下关系 批发量 批发单价（元 ‎6‎ ‎5‎ ‎（1）写出批发该种水果的资金金额（元与批发量之间的函数关系式；并在如图的坐标系网格中画出该函数图象；指出资金金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．‎ ‎（2）经市场调查，销售该种水果的日最高销量与零售价（元之间满足函数关系，小明同学拟每日售出以上该种水果（不考虑损耗），且当日零售价不变，请问他批发多少千克该种水果，零售价定为多少元时，能使当日获得的利润最大，最大利润是多少？‎ 八、（本题满分14分）‎ ‎23．（14分）如图，在中，，于点，是边上一点，连接交于点，作交于点．‎ ‎（1）求证：；‎ ‎（2）若是边的中点，‎ ‎①如图2，当时，求证：；‎ ‎②如图3，当时，探究的值，并说明理由．‎ ‎2019年安徽省合肥市蜀山区中考数学一模试卷 参考答案与试题解析 一、选择题（本大题共10小题，每小题4分.每小题都给出A、B、C、D四个选项，其中只有一个是正确的.）‎ ‎1．（4分）的倒数是　　‎ A．3 B． C． D．‎ ‎【解答】解：的倒数是3，‎ 故选：．‎ ‎2．（4分）计算所得结果是　　‎ A． B． C． D．‎ ‎【解答】解：，‎ 故选：．‎ ‎3．（4分）某手机芯片采用16纳米工艺纳米米），其中16纳米用科学记数法表示为　　‎ A．米 B．米 C． D．米 ‎【解答】解：16纳米米米 故选：．‎ ‎4．（4分）如图是一个几何体的三视图，根据图中所示数据求得这个几何体的侧面面积是　　‎ A． B． C． D．‎ ‎【解答】解：先由三视图确定该几何体是圆柱体，底面半径是，高是．‎ 所以该几何体的侧面积为．‎ 故选：．‎ ‎5．（4分）如图，在中，，平分，交于，，交于，则的大小是　　‎ A． B． C． D．‎ ‎【解答】解：在中，，‎ ‎，‎ 平分，‎ ‎，‎ ‎，‎ ‎．‎ 故选：．‎ ‎6．（4分）合肥市统计局资料显示，2016年全市生产总值为6274.3亿元，2018年全市生产总值为7822.9亿元，假设2017年，假如2017年与2018年这两年的年平均增长率均为，则下列方程式正确的是　　‎ A． ‎ B． ‎ C． ‎ D． ‎ ‎【解答】解：设2017年与2018年这两年的年平均增长率均为，‎ 根据题意得：‎ ‎，‎ 故选：．‎ ‎7．（4分）为了响应学校“皖疆手拉手，书香飘校园”的爱心捐书活动，励志班的同学们积极捐书，其中该班雄鹰小组的同学们捐书册数分别是：5，7，，3，4，6．已知他们平均每人捐5本，则这组数据的众数、中位数和方差分别是　　‎ A．5，5.5，10 B．5，5， C．5，5， D．6，5.5，‎ ‎【解答】解：由5，7，，3，4，6．已知他们平均每人捐5本，得 ‎．‎ 众数是5，中位数是5，‎ 方差，‎ 故选：．‎ ‎8．（4分）已知关于的一元二次方程有两个不相等的实数根，则实数的取值范围是　　‎ A． B． C． D．‎ ‎【解答】解：根据题意得△，‎ 解得．‎ 故选：．‎ ‎9．（4分）如图，，、相交于点，过点的直线分别交、于点、，则下列结论不一定成立的是　　‎ A． B． C． D．‎ ‎【解答】解：‎ ‎，，‎ 正确），，‎ 正确），‎ 正确）‎ 故选：．‎ ‎10．（4分）如图直线，都与直线垂直，垂足分别为、，，等腰直角的斜边，在直线上，，且点位于点处，将等腰直角沿直线向右平移，直到点与点重合为止，记点平移平移的距离为，等腰直角的边位于直线，之间部分的长度和为，则关于的函数图象大致为　　‎ A． B． ‎ C． D．‎ ‎【解答】解：①当时，如图1所示．‎ 此时，则，在中，利用勾股定理得，‎ 所以等腰直角的边位于直线，之间部分的长度和为，‎ 是一次函数，当时，点到达点，；‎ ‎[来源:学科网ZXXK]‎ ‎②当时，如图2所示，‎ 是等腰直角三角形，，，‎ 此时．‎ 即当时，的值不变是．‎ ‎③当时，如图3所示，‎ 此时是等腰直角三角形，，则，‎ ‎，是一次函数，当时，．‎ 综上所述只有答案符合要求．‎ 故选：．‎ 二、填空题（本大题共4小题，每小题5分，满分20分）‎ ‎11．（5分）方程的解是　1　．‎ ‎【解答】解：两边都乘以，得：，‎ 解得：，‎ 检验：时，，‎ 所以原分式方程的解为，‎ 故答案为：1．‎ ‎12．（5分）分解因式：　　．‎ ‎【解答】解：原式，‎ 故答案为：．‎ ‎13．（5分）如图，点在反比例函数的图象上，过点分别与轴和轴的垂线，垂足分别是和，点的坐标为，取轴上一点，，过点作轴的垂线交反比例函数图象于点，过点作线段交于点，得到矩形，依次在轴上取点 ，，，按此规律作矩形，则矩形为正整数）的面积为　　．‎ ‎【解答】解：第1个矩形的面积，‎ 第2个矩形的面积，‎ 第3个矩形的面积，‎ 第个矩形的面积．‎ 矩形为正整数）的面积为．‎ 故答案为：‎ ‎14．（5分）如图，在矩形中，，，过矩形的对角线交点作直线分别交、于点、，连接，若是等腰三角形，则　或4　．‎ ‎【解答】解：连接，如图1所示：‎ 四边形是矩形，‎ ‎，，，，‎ ‎，‎ 在和中，，‎ ‎，‎ ‎，若是等腰三角形，分三种情讨论：‎ ‎①当时，如图1所示：‎ 设，则，‎ 在中，由勾股定理得：，‎ 解得：，即；‎ ‎②当时，‎ 作于，如图2所示：‎ 则，‎ 设，则，，‎ ‎，解得：；‎ ‎③当时，作于，如图3所示：‎ 则，设，则，，‎ ‎，‎ 在中，由勾股定理得：，‎ 整理得：，‎ ‎△，‎ 此方程无解；‎ 综上所述：是等腰三角形，则为或4；‎ 故答案为：或4．‎ 三、（本大题共2小题，每小题8分，满分16分）‎ ‎15．（8分）计算：‎ ‎【解答】解：‎ ‎．‎ ‎16．（8分）先化简，再求值：，其中．‎ ‎【解答】解：原式 ‎．‎ 当时，原式．‎ 四、（本大题共2小题，每小题8分，满分16分）‎ ‎17．（8分）如图，在由边长为1个单位长度的小正方形组成的网格中，，，．‎ ‎（1）将先向下平移3个单位长度，再向左平移2个单位长度，作出平移后的△．‎ ‎（2）将△绕点逆时针旋转，作出旋转后的△．‎ ‎（3）在（2）的旋转过程中，点经过的路径长为　　．‎ ‎【解答】解：（1）如图，△为所作；‎ ‎（2）如图，△为所作；‎ ‎（3），‎ 所以点经过的路径长．‎ 故答案为．‎ ‎18．（8分）《九章算术》中有这样一道题，原文如下：‎ 今有甲乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而钱亦五十．问甲、乙持钱各几何？‎ 大意为：‎ 今有甲、乙二人，不知其钱包里有多少钱，若乙把其一半的钱给甲，则甲的钱数为50；若甲把其的钱给乙，问甲、乙各有多少钱？‎ 请解答上述问题．‎ ‎【解答】解：设甲持钱为，乙持钱为，‎ 根据题意，可列方程组：，‎ 解得．‎ 答：甲持钱为25，乙持钱为50．‎ 五、（本大题共2小题，每小题10分，满分20分）‎ ‎19．（10分）如图，、、三地在同一直线上，在的北偏东方向，在的北偏西方向，在的北偏西方向，且，求与之间的距离．‎ ‎【解答】解：过作于，，‎ ‎，‎ ‎，‎ 是等边三角形，‎ ‎，‎ ‎，‎ 与之间的距离为．‎ ‎20．（10分）如图，已知四边形的外接圆的半径为4，弦与的交点为，与相交于点，．‎ ‎（1）求证：；‎ ‎（2）若，，求的面积．‎ ‎【解答】（1）证明：‎ 又 而 即：得证．‎ ‎（2）连接，如下图所示[来源:学科网]‎ ‎，‎ 又 且 ‎，‎ 而 故的面积为．‎ 六、（本题满分12分）‎ ‎21．（12分）随着智能手机的普及率越来越高以及移动支付的快捷高效性，中国移动支付在世界处于领先水平，为了解人们平时最喜欢用哪种移动支付方式，因此在某步行街对行人进行随机抽样调查，以下是根据调查结果分别整理的不完整的统计表和统计图．‎ 移动支付方式 支付宝 微信 其他 人数人 ‎200‎ ‎75‎ 请你根据上述统计表和统计图提供的信息．完成下列问题 ‎（1）在此次调查中，使用支付宝支付的人数为　500　人，表示微信支付的扇形所对的圆心角度数为　　度．‎ ‎（2）某天该步行街人流量为10万人，其中的人购物并选择移动支付，请你依据此次调查获得的信息估计一下当天使用微信支付的人数．‎ ‎（3）甲、乙、丙三人都只习惯使用支付宝和微信支付，并且他们选择这两种支付的可能性是相同的，请计算三人恰好选择同一种支付方式的概率．‎ ‎【解答】解：（1）被调查的总人数为（人，‎ 使用支付宝支付的人数为（人，‎ 表示微信支付的扇形所对的圆心角度数为，‎ 故答案为：500，144；‎ ‎（2）估计当天使用微信支付的人数为（万人）；‎ ‎（3）画树状图如下：‎ 由树状图知，共有8种等可能结果，其中三人恰好选择同一种支付方式的有2种，‎ 所以三人恰好选择同一种支付方式的概率为．‎ 七、（本题满分12分）‎ ‎22．（12分）小明大学毕业后积极响应政府号召回乡创业，准备经营水果生意，他在批发市场了解到某种水果的批发单价与批发量有如下关系 批发量 批发单价（元 ‎6‎ ‎5‎ ‎（1）写出批发该种水果的资金金额（元与批发量之间的函数关系式；并在如图的坐标系网格中画出该函数图象；指出资金金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．‎ ‎（2）经市场调查，销售该种水果的日最高销量与零售价（元之间满足函数关系，小明同学拟每日售出以上该种水果（不考虑损耗），且当日零售价不变，请问他批发多少千克该种水果，零售价定为多少元时，能使当日获得的利润最大，最大利润是多少？‎ ‎【解答】解：（1）由图象可知，当资金金额时，以同样的资金可以批发到较多数量的该种水果．‎ ‎（2）销售该种水果的日最高销量与零售价（元之间满足函数关系，‎ 小明同学拟每日售出以上该种水果，则其批发单价为5元，设利润为元，则由题意得：‎ 当，时，时，能使当日获得的利润最大，最大利润为360元．‎ 答：他批发120千克该种水果，零售价定为8元时，能使当日获得的利润最大，最大利润是360元 八、（本题满分14分）‎ ‎23．（14分）如图，在中，，于点，是边上一点，连接交于点，作交于点．‎ ‎（1）求证：；‎ ‎（2）若是边的中点，‎ ‎①如图2，当时，求证：；‎ ‎②如图3，当时，探究的值，并说明理由．‎ ‎【解答】（1）证明：，，‎ ‎、、、四点共圆，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 同理，，‎ ‎，‎ ‎；‎ ‎（2）①证明：作交于，‎ 是边的中点，‎ 是边的中点，‎ ‎，，‎ ‎，[来源:学#科#网Z#X#X#K]‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎；‎ ‎②解：作交于，‎ ‎，‎ ‎，‎ ‎，‎ ‎，，‎ ‎，‎ ‎，‎ ‎，‎ 由①得，，‎ ‎，‎ ‎．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/6 17:20:41；用户：老王；邮箱：41608708@qq.com；学号：1007195‎