2019年全国中考真题分类汇编：与四边形有关的计算与证明 9页

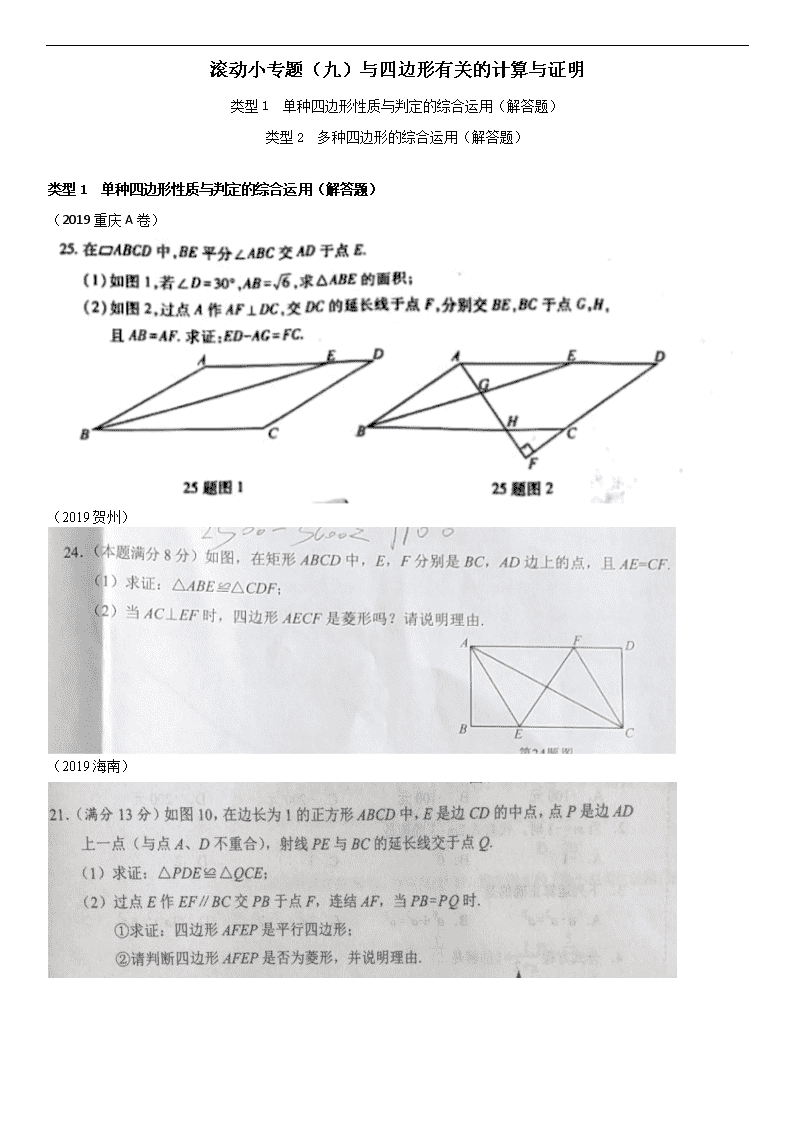
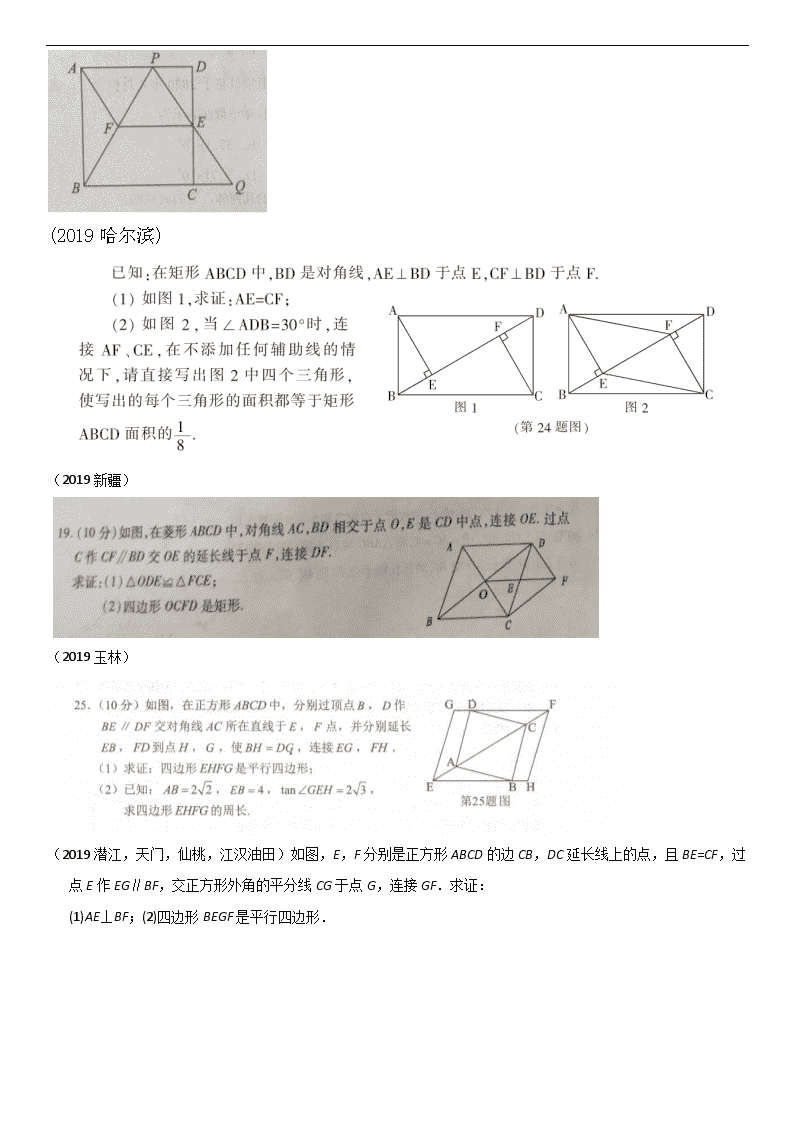
滚动小专题（九）与四边形有关的计算与证明 类型1　单种四边形性质与判定的综合运用（解答题）‎ 类型2　多种四边形的综合运用（解答题）‎ 类型1　单种四边形性质与判定的综合运用（解答题）‎ ‎（2019重庆A卷）‎ ‎（2019贺州）‎ ‎（2019海南）‎ ‎(2019哈尔滨)‎ ‎（2019新疆）‎ ‎（2019玉林）‎ ‎（2019潜江，天门，仙桃，江汉油田）如图，E，F分别是正方形ABCD的边CB，DC延长线上的点，且BE=CF，过点E作EG∥BF，交正方形外角的平分线CG于点G，连接GF．求证：‎ ‎(1)AE⊥BF；(2)四边形BEGF是平行四边形． ‎ ‎ (2019鄂州)如图，矩形ABCD中，AB＝8，AD＝6，点O是对角线BD的中点，过点O的直线分别交AB、CD边于点E、F.‎ ‎（1）求证：四边形DEBF是平行四边形;‎ ‎（2）当DE＝DF时，求EF的长.‎ 解：（1）证明：∵ 四边形ABCD是矩形 ‎ ‎ ∴ AB∥CD ‎ ∴ ∠DFO＝∠BEO，‎ ‎ 又因为∠DOF＝∠BOE，OD＝OB ‎ ∴△DOF ≌ △BOE ∴DF＝BE ‎ 又因为DF∥BE，‎ ‎ ∴四边形BEDF是平行四边形. ‎ ‎ （2）∵DE=DF，四边形BEDF是平行四边形 ‎ ∴ BEDF是菱形 ∴ DE＝BE，EF⊥BD，OE＝OF ‎ 设AE=x，则DE＝BE=8-x ‎ 在Rt△ADE中，根据勾股定理，有AE2+AD2＝DE2‎ ‎∴ x2+62= (8-x)2 解之得：x = ‎‎7‎‎4‎ ‎∴ DE=8 -‎ ‎‎7‎‎4‎ = ‎25‎‎4‎ ‎ 在Rt△ABD中，根据勾股定理，有AB2+AD2＝BD2‎ ‎∴BD=‎6‎‎2‎‎+‎8‎‎2‎ ‎‎=10‎ ∴ OD = ‎1‎‎2‎‎ ‎ BD = 5,‎ 在Rt△DOE中，根据勾股定理，有DE2 - OD2＝OE2，‎ ‎∴ OE = ‎‎(‎25‎‎4‎‎)‎‎2‎-‎5‎‎2‎ ‎‎= ‎15‎‎4‎ ‎ ‎∴ EF = 2OE=‎ ‎‎15 ‎‎2‎ ‎ ‎（此题有多种解法，方法正确即可分）‎ ‎（2019福建）‎ ‎（2019 枣庄）‎ ‎（2019重庆A卷）‎ ‎25．如图，在平行四边形ABCD中，点E在边BC上，连结AE，EM⊥AE，垂足为E，交CD于点M， AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P显AD上一点，连接CP．‎ ‎（1）若DP=2AP=4，CP=，CD=5，求△ACD的面积．‎ ‎（2）若AE=BN，AN=CE，求证：AD=CM+2CE．‎ ‎（2019 泰安）‎ ‎（2019 南充）‎ ‎（2019 安徽）‎ ‎（2019 凉山州）‎ ‎（2019 青岛）‎ ‎21．（本小题满分 8 分）‎ 如图，在□ABCD 中，对角线 AC 与 BD 相交于点 O ，点 E ， F 分别为 OB ， OD 的中点，延长 AE 至 G ，使 EG ＝AE ，连接 CG ．‎ ‎（1）求证： △ABE≌△CDF ；‎ ‎（2）当 AB 与 AC 满足什么数量关系时，四边形 EGCF 是矩形？请说明理由.‎ 答案：‎ 类型2　多种四边形的综合运用（解答题）‎ 22. ‎（2019宿迁）如图，矩形ABCD中，AB=4，BC=2，点E、F分别在AB、CD上，且BE=DF=3/2，‎ ‎⑴ 求证：四边形AECF是菱形[来源:学科网]‎ ‎⑵ 求线段EF的长.‎ ‎ ‎ ‎（2019 滨州）‎ ‎（2019 泰安）‎ ‎（2019 宁波）‎ 答案：‎