2020九年级数学下册 第二十七章 第2课时 相似三角形判定定理1，2同步练习 7页

1 课时作业(九) [27.2.1 第 2 课时 相似三角形判定定理 1，2] 一、 选择题 1．有甲、乙两个三角形木框，甲三角形木框的三边长分别为 1， 2， 5，乙三角形木框的三边长 分别为 5， 5， 10，则甲、乙两个三角形( ) A．一定相似 B．一定不相似 C．不一定相似 D．无法判断 2．图 K－9－2 中的四个三角形与图 K－9－1 中的三角形相似的是( ) 图 K－9－1 图 K－9－2 3．如图 K－9－3，四边形 ABCD 的对角线 AC，BD 相交于点 O，且将这个四边形分成①②③④四 个三角形．若 OA∶OC ＝ OB∶OD，则下列结论中一定正确的是( ) 图 K－9－3 A．①和②相似 B．①和③相似 C．①和④相似 D．③和④相似 4．已知线段 AD，BC 相交于点 O，OB∶OD＝3∶1，若 OA＝12 cm，OC＝4 cm，AB＝30 cm，则 CD 的长为( ) A．5 cm B．10 cm C．45 cm D．90 cm 5．如图 K－9－4，在方格纸中，△ABC 和△EPD 的顶点均在格点上，要使△ABC∽△EPD，则点 P 所在的格点为( ) 图 K－9－4 A．P1 B．P2 C．P3 D．P4 2 6．一个钢筋三角架的三边长分别为 20 cm，50 cm，60 cm，现在要做一个和它相似的钢筋三角 架，而只有长为 30 cm 和 50 cm 的两根钢筋，要求以其中的一根为一边，从另一根上截两段(允许有 余料)作为另两边，则不同的截法有( ) 链接听课例 1 归纳总结 A．一种 B．两种 C．三种 D．四种或四种以上 二、填空题 7．如图 K－9－5，D 是△ABC 内的一点，连接 BD 并延长到点 E，连接 AD，AE，若AD AB ＝DE BC ＝AE AC ， 且∠CAE＝29°，则∠BAD＝________°. 图 K－9－5 8．如图 K－9－6 所示，D 是∠ABC 平分线上的一点，AB＝15 cm，BD＝12 cm，要使△ABD∽△DBC， 则 BC 的长为________cm. 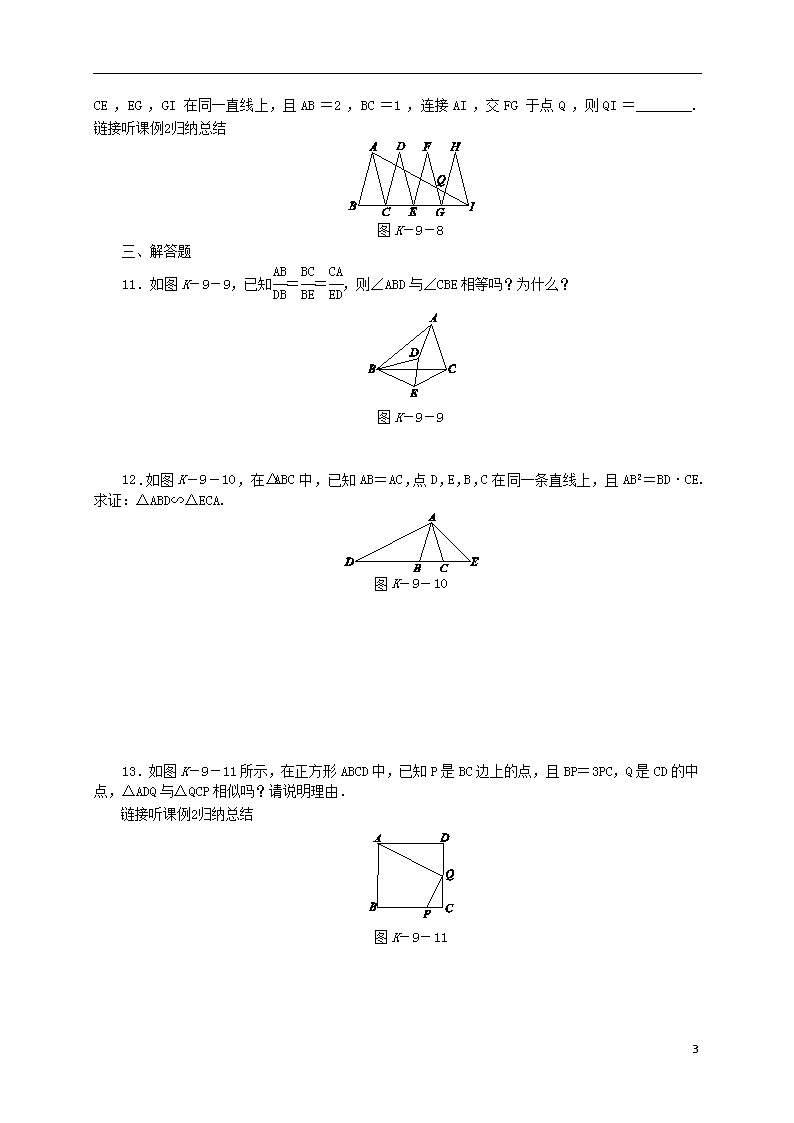图 K－9－6 9．如图 K－9－7 所示，正方形 ABCD 的边长为 2，AE＝EB，MN＝1，线段 MN 的两端分别在 CB， CD 上滑动，当 CM＝________时，△AED 与以 M，N，C 为顶点的三角形相似． 图 K－9－7 10．如图 K－9－8，已知△ABC，△DCE，△FEG，△HGI 是 4 个全等的等腰三角形，底边 BC，CE， EG，GI 在同一直线上，且 AB＝2，BC＝1，连接 AI，交 FG 于点 Q，则 QI＝________.链接听课例 2 归纳总结 图 K－9－8 三、解答题 11．如图 K－9－9，已知AB DB ＝BC BE ＝CA ED ，则∠ABD 与∠CBE 相等吗？为什么？ 3 图 K－9－9 12．如图 K－9－10，在△ABC 中，已知 AB＝AC，点 D，E，B，C 在同一条直线上，且 AB2＝BD·CE. 求证：△ABD∽△ECA. 图 K－9－10 13．如图 K－9－11 所示，在正方形 ABCD 中，已知 P 是 BC 边上的点，且 BP＝3PC，Q 是 CD 的中 点，△ADQ 与△QCP 相似吗？请说明理由． 链接听课例 2 归纳总结 图 K－9－11 14．如图 K－9－12，在△ABC 中，点 D，E 分别在边 AB，AC 上，∠AED＝∠B，射线 AG 分别交线 段 DE，BC 于点 F，G，且AD AC ＝DF CG . (1)求证：△ADF∽△ACG； (2)若AD AC ＝1 2 ，求AF FG 的值． 4 图 K－9－12 动 态探究如图 K－9－13，在 Rt△ABC 中，∠A＝90°，BC＝10 cm，AC＝6 cm，在线段 BC 上，动点 P 以 2 cm/s 的速度从点 B 向点 C 匀速运动；同时在线段 CA 上，点 Q 以 a cm/s 的速度从点 C 向点 A 匀 速运动，当点 P 到达点 C(或点 Q 到达点 A)时，两点停止运动． (1)当点 P 运动30 11 s 时，△CPQ 与△ABC 第一次相似，求点 Q 的速度； (2)在(1)的条件下，当△CPQ 与△ABC 第二次相似时，求点 P 总共运动了多少秒． 图 K－9－13 5 详解详析 [课堂达标] 1．[解析] A 因为 5 1 ＝ 10 2 ＝ 5 5 ＝ 5，即两个三角形的三边对应成比例，所以甲、乙两个三 角形一定相似． 2．[解析] B 设网格中小正方形的边长为 1.首先判断出题图中的三角形是直角三角形，根据 勾股定理求出两直角边长分别是 2和 2 2，然后根据两边成比例且夹角相等的三角形相似可知选 B. 3．[解析] B 两个三角形两边的比相等，并且相应的夹角相等，那么这两个三角形相似． 4．[解析] B ∵OB OD ＝OA OC ＝3 1 ，∠AOB＝∠COD，∴△AOB∽△COD， ∴AB CD ＝OB OD ，即30 CD ＝3 1 ， ∴CD＝10 (cm)．故选 B. 5．[解析] C ∵∠BAC＝∠PED， 且AB AC ＝3 2 ， ∴当EP ED ＝3 2 时，△ABC∽△EPD. ∵DE＝4，∴EP＝6，∴点 P 落在 P3 处． 6．[解析] B 由相似三角形对应边成比例可知，只能将 30 cm 长的一根作为一边，再从 50 cm 长的一根上截下两段． 设从 50 cm 长的钢筋上截下的两段分别长 x cm，y cm(x＜y)， 当 30 cm 长的边对应 20 cm 长的边时，20 30 ＝50 x ＝60 y ，∴x＝75 cm，x＞50 cm，不成立； 当 30 cm 长的边对应 50 cm 长的边时，20 x ＝50 30 ＝60 y ，∴x＝12 cm，y＝36 cm，x＋y＝48 cm＜50 cm，成立； 当 30 cm 长的边对应 60 cm 长的边时，20 x ＝50 y ＝60 30 ，∴x＝10 cm，y＝25 cm，x＋y＝35 cm＜50 cm，成立．故有两种截法．故选 B. 7．[答案] 29 6 [解析] ∵AD AB ＝DE BC ＝AE AC ， ∴△ADE∽△ABC， ∴∠DAE＝∠BAC， 即∠BAD＋∠DAC＝∠DAC＋∠CAE， ∴∠BAD＝∠CAE＝29°. 8．[答案] 48 5 [解析] ∵△ABD∽△DBC， ∴AB DB ＝BD BC ，∴BC＝BD2 AB ＝12 15 2＝48 5 (cm)． 9．[答案] 5 5 或2 5 5 [解析] 只需AD CM ＝AE CN 或AD CN ＝AE CM ，即可得这两个三角形相似，但它们的比值都等于DE MN . ∵AD＝2，AE＝1，∴DE＝ 5， ∴ 2 CM ＝ 5 1 或 1 CM ＝ 5 1 ， ∴CM＝2 5 5 或 CM＝ 5 5 . [点评] 弄清两个三角形相似需具备的条件和各种情形． 10．[答案] 4 3 [解析] ∵△ABC，△DCE，△FEG，△HGI 是 4 个全等的等腰三角形，∴HI＝AB＝2，GI＝BC＝1， BI＝4BC＝4， ∴AB BI ＝2 4 ＝1 2 ，BC AB ＝1 2 ， ∴AB BI ＝BC AB . 又∵∠ABI＝∠ABC， ∴△ABI∽△CBA， ∴AC AI ＝AB BI . ∵AB＝AC，∴AI＝BI＝4. ∵∠ACB＝∠FGE，∴AC∥FG， ∴QI AI ＝GI CI ＝1 3 ，∴QI＝1 3 AI＝4 3 . 11．解：∠ABD＝∠CBE.理由如下： 因为AB DB ＝BC BE ＝CA ED ，所以△BAC∽△BDE， 所以∠ABC＝∠DBE， 则∠ABC－∠DBC＝∠DBE－∠DBC， 即∠ABD＝∠CBE. 12．证明：∵AB＝AC，∴∠ABC＝∠ACB， ∴∠ABD＝∠ACE. ∵AB2＝BD·CE， ∴AB CE ＝BD AB ，即AB EC ＝BD CA ， ∴△ABD∽△ECA. 7 13．[解析] △ADQ 与△QCP 中已有一角对应相等，条件中告诉了边之间的关系，判断两三角形 是否相似，就是看夹已知角的两边是否对应成比例． 解：相似．理由如下： 设 PC＝a，则 BP＝3a，BC＝BP＋PC＝4a. ∵Q 是 CD 的中点，∴DQ＝QC＝1 2 CD＝2a， ∴AD QC ＝4a 2a ＝2，DQ CP ＝2a a ＝2，∴AD QC ＝DQ CP . 又∵∠D＝∠C＝90°，∴△ADQ∽△QCP. [点评] 当两个三角形中已有一个角对应相等时，要判定两三角形相似，只需证明夹这个角的两 边对应成比例即可． 14．解：(1)证明：因为∠AED＝∠B，∠DAE＝∠CAB， 所以∠ADF＝∠C. 又因为 AD AC ＝DF CG ，所以△ADF∽△ACG. (2)因为△ADF∽△ACG，所以AD AC ＝AF AG . 又因为 AD AC ＝1 2 ，所以AF AG ＝1 2 ，所以AF FG ＝1. [素养提升] 解：(1)如图①，BP＝30 11 ×2＝60 11 (cm)． 依题意，知当QC AC ＝PC BC 时，△CPQ 与△ABC 第一次相似， 即 30a 11 6 ＝ 10－60 11 10 ，解得 a＝1， ∴点 Q 的速度为 1 cm/s. (2)如图②，设点 P 运动了 t s. 依题意，知当QC BC ＝PC AC 时，△CPQ 与△ABC 第二次相似，即 t 10 ＝10－2t 6 ，解得 t＝50 13 ， ∴点 P 总共运动了50 13 s.