2013学年上海市初三年级数学学科质量调研测试(含答案) 13页

2013 学年初三年级数学学科质量调研测试 （时间：100 分钟 满分：150 分） 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） 1、如果△ ABC∽△DEF（其中顶点 A、B、C 依次与顶点 D、E、F 对应），那么下列等式中 不一定成立的是（ ▲ ） A、∠A＝∠D B、 AD BE  C、AB＝DE D、 AB DE AC DF 2、如图，地图上 A 地位于 B 地的正北方，C 地位于 B 地的北偏东 50°方向，且 C 地到 A 地、 B 地距离相等，那么 C 地位于 A 地的（ ▲ ） A、南偏东 50°方向 B、北偏西 50°方向 C、南偏东 40°方向 D、北偏西 40°方向 3、将抛物线 2yx 向左平移 2 个单位，则所得的抛物线的解析式为（ ▲ ） A、 2( 2)yx B、 2( 2)yx C、 2 2yx D、 2 2yx 4、如图，△ PQR 在边长为 1 个单位的方格纸中，它的顶点在小正方形顶点位置，其中点 A、 B、C、D 也是小正方形的顶点，那么与△ PQR 相似的是（ ▲ ） A、以点 P、Q、A 为顶点的三角形 B、以点 P、Q、B 为顶点的三角形 C、以点 P、Q、C 为顶点的三角形 D、以点 P、Q、D 为顶点的三角形 5、抛物线 2 32y x x   与坐标轴（含 x 轴、y 轴）的公共点的个数是（ ▲ ） A、0 B、1 C、2 D、3 6、如图，在△ ABC 中，∠ACB＝90°，CD 为边 AB 上的高，已知 BD＝1，则线段 AD 的长 是（ ▲ ） A、 2sin A B、 2cos A C、 2tan A D、 2cot A 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） C B A （第 2 题） Q R P D C B A （第 4 题） A B D C （第 6 题） 7、已知 7 4 x y  ，则 xy xy   的值为 ▲ 。 8、计算： 2( ) 3( )a b a b    ▲ 。 9、已知两个相似三角形的周长比为 2:3，且其中一个三角形的面积是 36，那么另一个三角 形的面积是 ▲ 。 10、已知第一象限内一点 A，已知 OA＝5，OA 与 x 轴正半轴形成的夹角为 ，且 tan 2  ， 那么点 A 的坐标是 ▲ 。 11、某人沿着一个坡比为1:3 的斜坡（AB）向前行走了 10 米，那么他实际上升的垂直高度 是 ▲ 米。 12、抛物线 2 23y x x   的顶点坐标是 ▲ 。 13、已知二次函数 ()y f x 图像的对称轴是直线 2x  ，如果 (3) (4)ff＞ ，那 么 ( 3)f  ▲ ( 4)f  。（填“＞”或“＜”） 14、正方形 ABCD 的边长为 6，圆 O 过 B、C 两点， 圆 O 的半径为 10 ，联结 AO，则∠BAO 的余切值是 ▲ ． 15、如图 1，将矩形 ABCD 的四个角向内折起，恰好拼成一个无缝隙 无重叠的四边形 EFGH，EH = 12，EF = 16，则边 AD 的长是 ▲ ． 16、已知点 P 是二次函数 2 24y x x   图像上的点，且它到 y 轴的距离为 2，则点 P 的坐 标是 ▲ 。 17、如图，E 是正方形 ABCD 边 CD 的中点，AE 与 BD 交于点 O， 则 tan AOB ▲ 。 18、在平面直角坐标系中，点 A 的坐标为 3,0 ，点 B 为 y 轴正 半轴上的一点，点C 是第一象限内一点，且 2AC  ．设 cot BOC m，则 m 的取值范 围是 ▲ 。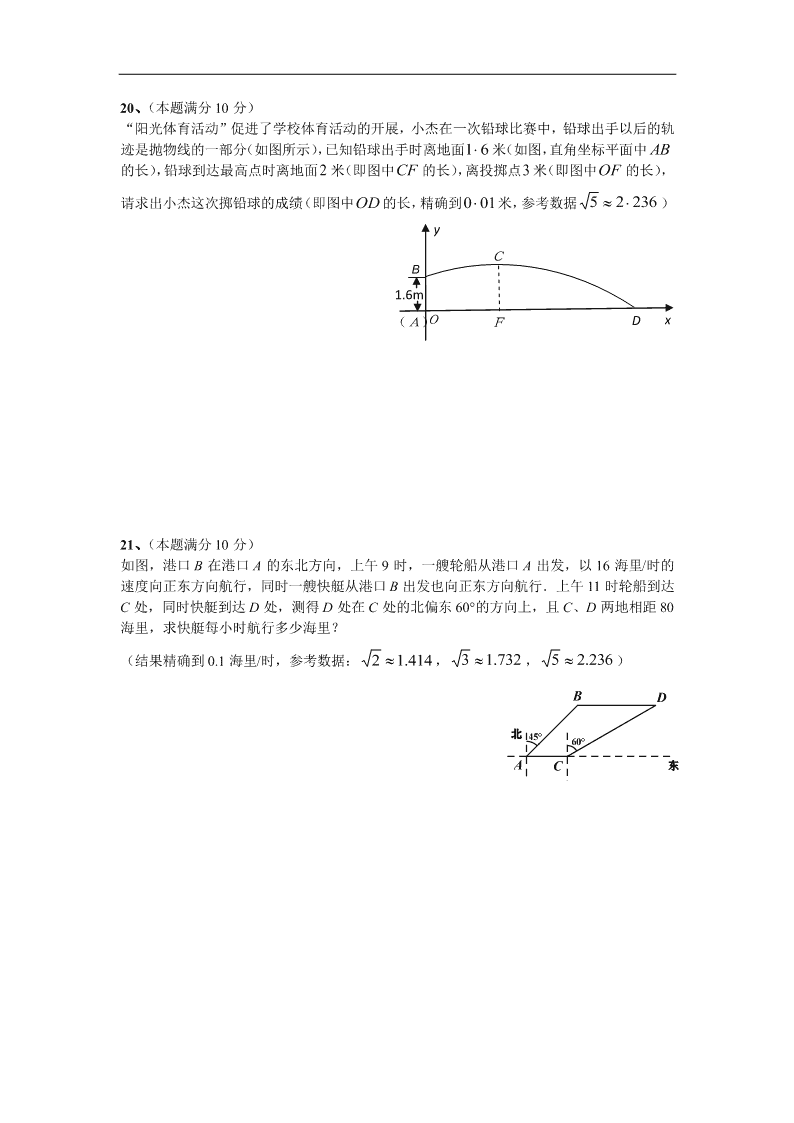 三、解答题：（本大题共 7 题，满分 78 分） 19、（本题满分 10 分）计算：    30sin 45cot60sin 60cos30tan 45cos A B C D E A B E D F C H G 图 1 图 2 20、（本题满分 10 分） “阳光体育活动”促进了学校体育活动的开展，小杰在一次铅球比赛中，铅球出手以后的轨 迹是抛物线的一部分（如图所示），已知铅球出手时离地面 61 米（如图，直角坐标平面中 AB 的长），铅球到达最高点时离地面 2 米（即图中CF 的长），离投掷点3 米（即图中OF 的长）， 请求出小杰这次掷铅球的成绩（即图中OD的长，精确到 010 米，参考数据 23625  ） 21、（本题满分 10 分） 如图，港口 B 在港口 A 的东北方向，上午 9 时，一艘轮船从港口 A 出发，以 16 海里/时的 速度向正东方向航行，同时一艘快艇从港口 B 出发也向正东方向航行．上午 11 时轮船到达 C 处，同时快艇到达 D 处，测得 D 处在 C 处的北偏东 60°的方向上，且 C、D 两地相距 80 海里，求快艇每小时航行多少海里？ （结果精确到 0.1 海里/时，参考数据： 414.12  ， 732.13  ， 236.25  ） 东 60°45°北 C DB A B 1.6m Ｃ Ｃ Ｆ Ｃ （Ａ） Ｏ y x D 22、（本题满分 10 分，第（1）小题 3 分，第（2）小题 3 分，第（3）小题 4 分） 已知：⊙O 的半径 OA=5，弦 AB=8，C 是弦 AB 的中点，点 P 是射线 AO 上一点（与点 A 不重合），直线 PC 与射线 BO 交于点 D。 （1）当点 P 在⊙O 上，求 OD 的长。 （2）若点 P 在 AO 的延长线上，设 OP=x， yDB OD  ，求 y 与 x 的函数关系式并写出自变量 x 的取值范围。 （3）连接 CO，若△ PCO 与△ PCA 相似，直接写出此时 BD 的长。 23、（本题满分 12 分，每小题 4 分） 在平面直角坐标系 xOy 中，二次函数 21 2y x bx c   的图象经过点 A（-3，6），并与 x 轴 交于点 B（-1，0）和点 C，顶点为 P． （1）求二次函数的解析式； （2）设 D 为线段 OC 上的一点，若 DPC BAC   ，求点 D 的坐标； （3）在（2）的条件下，若点 M 在抛物线 上，点 N 在 y 轴上，要使以 M、 N、B、D 为顶点的四边形是平行四边形，这样的点 M、N 是否存在，若存在，直接写出所 有满足条件的点 M 的坐标；若不存在，说明理由． （第 22 题图） D P O C B A （备用图） O C B A （备用图） O C B A 24、（本题满分 12 分，每小题 4 分） 如图，已知抛物线过点 (0,6)A ， (2,0)B ， 5(7, )2C 。 （1）求抛物线的解析式； （2）若 D 是抛物线的顶点， E 是抛物线的对称轴与直线 AC 的交点， F 与 E 关于 D 对称， 求证： CFE AFE   ； （3）在 y 轴上是否存在这样的点 P ，使 AFP 与 FDC 相似，若有，请求出所有符合条件 的点 P 的坐标；若没有，请说明理由。 y x A B O D F C E （第 24 题图） 25、（本题满分 14 分，第（1）小题 4 分，第（2）小题 6 分，第（3）小题 4 分） 如图，在△ ABC 中，∠ACB＝90°，AC＝6，BC＝8，CD 是 AB 上的中线，点 E 是边 BC 上 一动点（不与 B、C 重合），设 BE=x。直线 DE 交直线 AC 于点 F。 （1）设 AF=y，求 y 与 x 的函数解析式及定义域； （2）①当△ CEF 是等腰三角形，求 x 的值； ②当以 C、E、F 为顶点的三角形与△ ABC 相似，求 x 的值； （3）若 S△ BED ＝ 1 4 S△ AFD ，直接写出直线 DE 与 AB 所夹锐角的正切值。 A B C D A B C D A B C D 第 25 题图 备用图 备用图 2013 学年初三年级数学学科质量调研测试 参考答案及评分标准 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） 1、C 2、A 3、A 4、B 5、D 6、B 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 7、11 3 8、5ab 9、16 或 81 10、( 5,2 5) 11、 10 12、( 1,2) 13、＞ 14、7 3 或 5 3 15、20 16、(2,4) 或( 2,12) 17、3 18、 250 5m 三、解答题：（本大题共 7 题，满分 78 分） 19、（本题满分 10 分） 解：原式 2 1 12 3 2 1 3 3 2 2     ………………………………………………6 分 36  ………………………………………………4 分 20、（本题满分 10 分） 解：由题意得 )6.1,0(B 、 )2,3(C ………………………………………2 分 设抛物线解析式 2)3( 2  xay （a ≠0 ）………………………1 分 将 代入，得 6.12)30( 2 a 解得 45 2a ……2 分 ∴抛物线解析式 2)3(45 2 2  xy ……………………………1 分 设 )0,(xD 代入，得 02)3(45 2 2  x 解得 533x （负值舍去） …………………………………2 分 ∴ 71.9708.9236.233533 x （米）……………1 分 答：小杰这次掷铅球的成绩是 71.9 米．…………………………………1 分 21、（本题满分 10 分） 解：分别过点 B、D 作 AC 的垂线，交 AC 的延长线于点 E、F，……1 分 在 Rt△DCF 中，∠DFC＝90°，∠DCF＝90°－60°＝30°，………………1 分 ∴ 402 1  CDDF 340cos  DCFCDCF ∴AF＝AC＋CF＝ 34032340216  ……………………………2 分 ∵DF⊥AF，BE⊥AF，BE⊥BD， ∴四边形 BEFD 是矩形. ∴BE＝DF＝40 在 Rt△BAE 中，∠BEA＝90°，∠BAE＝90°－45°＝45°， ∴AE＝BE＝40 ……………………………1 分 ∴ 83404034032  AEAFEF . ∴ 8340  EFBD …………………………………………………………2 分 6.3043202)8340(  .………………………………………2 分 答：快艇的速度约为 30.6 海里/时。……………………………1 分 22、（本题满分 10 分，第（1）小题 3 分，第（2）小题 3 分，第（3）小题 4 分） 解：当 P 在⊙O 上时，连接 BP …………………………………………（1 分） ∵ C 是 AB 中点，O 是 AP 中点， ∴ 点 D 为△ ABP 的重心， ∴ 1 3OD OB …………………………………（1 分） ∵ OA=OB=5 ∴ 5 3OD  ……………………………………………………（1 分） （2）过点 O 作 OE//AB，交 PC 于点 E（如图） ∵OE//AB ∴ OE OP AC AP ， OE OD BC BD 又∵ AC=BC ∴ OP OD AP BD …………………………………………………（1 分） 即 5 xy x  (x>0) …………………………………………………………（1 分+1 分） (3) 当 P 在 AO 延长线上时，若△ PCO∽△PAC 时，有∠PCO=∠A， ∵∠A=∠B，∴∠PCO=∠B， 易证△ ACO∽△BDC 得 AC AO BD BC 得 45 4BD  ∴ 16 5BD  ………………………………（2 分） 当 P 在 AO 上时，若△ PCO∽△PAC 时，可得 CP⊥AO（如图） 作 BH⊥AO，可求得 9 5PO  ， 7 5OH  由 OP OD OH OB ， 得 9 5 7 5 5 OD ∴ 45 7OD  则 45 80577BD OB OD     ……………………………………………（2 分） 45° E FC DB A P O D HA B C D O PA B C E 综上所述，若△ PCO 与△ PCA 相似，此时 BD 的长为16 5 或 80 7 （其他解法略） 23、（本题满分 12 分，每小题 4 分） 解：（1）将点 A（-3，6）， B（-1，0）代入 21 2y x bx c   中， 得 9 3 6,2 1 0.2 bc bc         ……………………………（1 分） 解得 1, 3.2 b c   ……………………………………………（2 分） ∴二次函数的解析式为 213 22y x x   ．……………………………（1 分） （2）令 0y  ，得 213022xx   ，解得 1 1x  ， 2 3x  ． ∴点 C 的坐标为（3，0）． ……………………………（1 分） ∵ 221 3 1 ( 1) 22 2 2y x x x      ， ∴顶点 P 的坐标为（1，-2）． ……………………………（1 分） 过点 A 作 AE⊥x 轴，过点 P 作 PF⊥x 轴，垂足分别为 E，F． 易得 45ACB PCD     ． 2262AC AE CE   ， 2222PC PF CF   ． 又 DPC BAC   ， ∴△ ACB∽△ PCD．……………………………（1 分） ∴ BC AC CD PC ． ∵ 3 ( 1) 4BC     ， ∴ 4 3 BC PCCD AC． ∴ 453 33OD OC CD     ． ∴点 D 的坐标为 5( , 0)3 ．……………………………（1 分） （3）当 BD 为一边时，由于 8 3BD  ， ∴点 M 的坐标为 8 85( , )3 18 或 8 11( , )3 18 ． ……………………………（2 分） 当 BD 为对角线时，点 M 的坐标为 2 35( , )3 18 ． ……………………………（2 分） 24．（本题满分 12 分，每小题 4 分） 解：（1）设经过 A（0，6）， B（2，0）， C（7， 5 2 ）三点的抛物线的解析式为 cbxaxy  2 ………………………………………1 分 则： 6 4 2 0 549 7 2 c a b c a b c             ……………………………………………………1 分 解得 1 , 4, 6.2a b c    ………………………………………………1 分 ∴ 此抛物线的解析式为 21 462y x x   ……………………………1 分 （2）过点 A 作 AM∥x 轴，交 FC 于点 M，交对称轴于点 N. ∵抛物线的解析式 可变形为  21 422yx   ∴抛物线对称轴是直线 x =4，顶点 D 的坐标为（4，－2），则 AN=4. 设直线 AC 的解析式为 11y k x b, 则有 1 11 6 57 2 b kb   ，解得 11 1 ,62kb   . ∴直线 AC 的解析式为 1 6.2yx   …………………………………1 分 当 x=4 时， 1 4 6 4.2y      ∴点 E 的坐标为（4，4）， ∵点 F 与 E 关于点 D 对称，则点 F 的坐标为（4，－8）……………1 分 设直线 FC 的解析式为 22y k x b, 则有 22 22 48 57 2 kb kb     ，解得 22 7 , 222kb   . ∴直线 FC 的解析式为 7 22.2yx ∵AM 与 x 轴平行，则点 M 的纵坐标为 6. 当 y=6 时，则有 7 22 6,2 x 解得 x=8. ∴AM=8,MN=AM—MN=4 ∴AN=MN ∵FN⊥AM ∴∠ANF=∠MNF 又 NF=NF ∴△ANF≌△MNF…………………………………………………1 分 ∴∠CFE=∠AFE……………………………………………………1 分 （3）∵C 的坐标为（7， 5 2 ）， F 坐标为（4，－8） ∴   2 25 3 538 7 422CF      ∵A 的坐标为（0，6）， ∴  2 26 8 4 2 53FA     ， 又 DF=6， ∵EF∥AO，则有∠PAF=∠AFE 又由（2）可知∠DFC=∠AFE ∴∠PAF=∠DFC 若△ AFP1∽△FCD 则 1PA AF DF CF ,即 1 2 53 6 3 53 2 PA ,解得 P1A=8…………………………1 分 ∴O P1=8－6=2 ∴P1 的坐标为（0，－2）……………………1 分 若△ AFP2∽△FDC 则 2PA AF CF DF ,即 2 2 53 63 53 2 PA  ,解得 P2A= 53 2 ……………………1 分 ∴O P2= －6= 41 2 ∴P2 的坐标为（0，－ ）…………1 分 所以符合条件的点 P 的坐标有两个，分别是 P1（0，－2）， P2（0，－ ）。 25、（本题满分 14 分，第（1）小题 4 分，第（2）小题 6 分，第（3）小题 4 分） （1）①当点 F 在 AC 延长线上时 过 D 作 DG⊥BC 于 G，则△ EDG∽△EFC ∴ DG CF ＝ EG CE ，∴ 3 CF ＝ x－4 8－x ，∴CF＝ 24－3x x－4 ∴AF＝AC＋CF＝6＋ 24－3x x－4 ＝ 3x x－4 即 y= 3x x－4 （4＜x＜8）……………………………2 分 ②当点 F 在 CA 延长线上时 过 D 作 DH⊥AC 于 H，则△ DFH∽△EFC ∴ HF CF ＝ DH CE ，∴ 3＋AF 6＋AF ＝ 4 8－x ，∴AF＝ 3x 4－x 即 y= 3x 4－x （0＜x＜4）……………………………2 分 注：定义域写错最多扣一分。 （2）①1°当点 F 在 AC 延长线上时 ∵∠ACB＝90°，∴DG∥AC ∵CD 是 AB 上的中线，∴AD＝BD ∴DG 是△ ABC 的中位线，∴DG＝ 1 2 AC＝3，BG＝ 1 2 BC＝4 ∵∠ACB＝90°，∴∠ECF＝90° ∵△CEF 是等腰三角形，∴∠CEF＝45° ∴∠DEG＝45°，∴△CEF 是等腰直角三角形 ∴EG＝DG＝3 ∴BE＝BG＋EG＝4＋3＝7 ……………………………1 分 2°当点 F 在 CA 延长线上时 ∵∠ACB＝90°，△ CEF 是等腰三角形，∴∠CEF＝45° ∴EG＝DG＝3 ∴BE＝BG－EG＝4－3＝1 ……………………………1 分 ∴BE 的长为 1 或 7 注：若学生做出一解即可得 2 分，两解全做出可得 3 分。 ②1°∵∠ACB＝90°，AC＝6，BC＝8，∴AB＝10 ∵CD 是 AB 上的中线，∴AD＝BD＝5 当点 F 在 AC 延长线上时 若∠CEF＝∠B，则∠BED＝∠CEF＝∠B， ∵CD 是斜边 AB 上的中线，∴∠BCD＝∠B ∴点 E 与点 C 重合，此时△ CEF 不存在 若∠F＝∠B，∵∠ECF＝∠ACB＝90° ∴△EFC∽△ABC 在△ AFD 和△ ABC 中，∵∠F＝∠B，∠A＝∠A ∴∠ADF＝∠ACB＝90° ∴BE＝ BD cosB ＝ 5 8 10 ＝ 25 4 A B C D E F A B C D E F G A B C D E F G A B C D E F H 2°当点 F 在 CA 延长线上时 ∵∠CAB＞∠F，∴当∠F＝∠B 时，△ EFC∽△ABC 过 D 作 DH⊥AC 于 H 则 AH＝CH＝ 1 2 AC＝3，DH＝ 1 2 BC＝4 ∴HF＝DH·cotF＝DH·cotB＝4× 8 6 ＝ 16 3 ∴CF＝CH＋HF＝3＋ 16 3 ＝ 25 3 ∴CE＝CF·tanF＝CF·tanB＝ 25 3 × 6 8 ＝ 25 4 ∴BE＝BC－CE＝8－ 25 4 ＝ 7 4 注：若学生做出一解即可得 2 分，两解全做出可得 3 分。 若学生第（2）小题都只做出一解，并都正确，最多得 3 分 （3）分别过 E、F 作 AB 的垂线，垂足为 M、N ①当点 F 在 AC 延长线上时 ∵AD＝BD，∴ S△ BED S△ AFD ＝ EM FN ∵S△ BED ＝ 1 4 S△ AFD ，∴ EM FN ＝ 1 4 ，∴ DE DF ＝ 1 4 ，∴ DE EF ＝ 1 3 过 D 作 DG⊥BC 于 G，则△ EDG∽△EFC ∴ EG CE ＝ DE EF ＝ 1 3 ，∴EG＝ 1 3 CE＝ 1 4 CG＝ 1 4 ×4＝1 ∴BE＝BG＋EG＝4＋1＝5，∴EM＝BE·sinB＝5× 6 10 ＝3 BM＝BE·cosB＝5× 8 10 ＝4，DM＝BD－BM＝5－4＝1 ∴tan∠EDB＝ EM DM ＝3……………………………2 分 ②当点 F 在 CA 延长线上时 ∵AD＝BD，∴ S△ BED S△ AFD ＝ EM FN ＝ 1 4 ，∴ DE DF ＝ 1 4 ，∴ DF EF ＝ 4 5 过 D 作 DH⊥AC 于 H，则△ DFH∽△EFC ∴ DH CE ＝ DF EF ＝ 4 5 ，∴CE＝ 5 4 DH＝ 5 4 ×4＝5 ∴BE＝BC－CE＝8－5＝3 ，∴EM＝BE·sinB＝3× 6 10 ＝ 9 5 BM＝BE·cosB＝3× 8 10 ＝ 12 5 ，DM＝BD－BM＝5－ 12 5 ＝ 13 5 ∴tan∠EDB＝ EM DM ＝ 9 13 ……………………………2 分 A B C D E F H M N A B C D E F G M N