2014年1月长宁中考数学一模试题 8页

长宁区九年级数学学科期末练习卷（2014 年 1 月） （考试时间：100 分钟，满分：150 分） 一、 选择题（本大题共 6 题，每题 4 分，满分 24 分） 1．下列说法中,结论错误的是（ ） A．直径相等的两个圆是等圆； B．长度相等的两条弧是等弧； C．圆中最长的弦是直径； D．一条弦把圆分成两条弧,这两条弧可能是等弧． 2．已知非零向量 ,,abc，下列条件中，不能．．判定 //ab的是（ ） A． ab ； B． ab ； C． // , //a c b c ； D． 2 , 4a c b c． 3．抛物线 2( 1) 3yx    的顶点坐标是（ ） A．( 1 , 3)； B．(1 , 3) ； C． ( 1 ,3) ； D．(1 ,3) ． 4．抛物线 2 41y x x   可以通过平移得到 2yx ，则下列平移过程正确的是（ ） A．先向左平移 2 个单位，再向上平移 3 个单位； B．先向左平移 2 个单位，再向下平移 3 个单位； C．先向右平移 2 个单位，再向下平移 3 个单位； D．先向右平移 2 个单位，再向上平移 3 个单位． 5．在△ABC 中，∠ACB = 90°，CD⊥AB 于 D，下列各组边的比不能．．表示sin B 的（ ） A． AC AB ； B． DC AC ； C． DC BC ； D． AD AC ． 第5题图 DA B C 第6题图 M P A D B C N a b c m n 第8题图 B D FE C A 6．如图，P 是平行四边形 ABCD 的对称中心，以 P 为圆心作圆，过 P 的任意直线与圆相交于点 M、N．则 线段 BM、DN 的大小关系是（ ） A．BM > DN； B．BM < DN； C．BM = DN； D．无法确定． 二、填空题（本大题共 12 题，每题 4 分，满分 48 分） 7．已知两个相似三角形的面积比是 4 : 1，则这两个三角形的周长比是 ． 8．如图，直线 // //abc，直线 mn、 与 a b c、 、 分别交于点 A、C、E、B、D、F，已知 AC=4，CE = 6， BD = 3，则 BF 等于 ． 9．将二次函数 224y x x配方成 2()y a x m k   的形式，配方后的解析式为 ． 10．如图，望大伯屋后有一块长 12 米，宽 8 米的矩形空地 ABCD，他在以较长边 BC 为直径的半圆形内中 菜，他家养的羊平时栓在 A 处的一棵树上，为了不让羊吃到菜，栓羊的绳长应小于 ． 第10题图 CD A B 第18题图 FE B C A D 11．已知抛物线 2 4 ( 2)y mx x m m    经过坐标原点，则实数 m 的值是 ． 12．已知抛物线 22y x bx c   经过点 A（0 , 3）、B（4 , 3），则此抛物线的对称轴是 ． 13．已知⊙A 的半径为 5，圆心 A（3 , 4），坐标原点 O 与⊙A 的位置关系是 ． 14．印刷厂 10 月份印刷一畅销小说书 5 万册，因购买此书人数激增，印刷厂需加印，若设印书量每月的 增长率为 x，12 月印书量 y 万册，写出 y 关于 x 的函数解析式 ． 15．在 Rt△ABC 中，∠C=90°，中线 AF 和中线 BE 交于点 G，若 AB = 3，则 CG= ． 16．某一山坡，坡长 200 米，山坡的高度 100 米，则此山坡的坡度是 ． 17．已知点 1 2 3(0 , ) (1 , ) (3 , )A y B y C y、 、 在抛物线 2 2 1 ( 0)y ax ax a    上，则 1 2 3y y y、 、 的大小 关系是 ． 18．如图，△ABC 是面积为 3 的等边三角形，△ADE∽△ABC，AB = 2AD，∠BAD = 45°，AC 与 DE 相 交于点 F，则△AEF 的面积是 ． 三、解答题（本大题共 7 题，满分 78 分） 19．（本题满分 10 分） 计算： 2013( tan 45 ) cos60 | cot30 1|      ． 20．（本题满分 10 分） 如图，在梯形 ABCD 中，AD // BC，AD = 2，BC = 3，EF 是梯形的中位线，EF 与 BD 交于点 M．设 AD a ， 试用 a 表示 BC 与 FM . 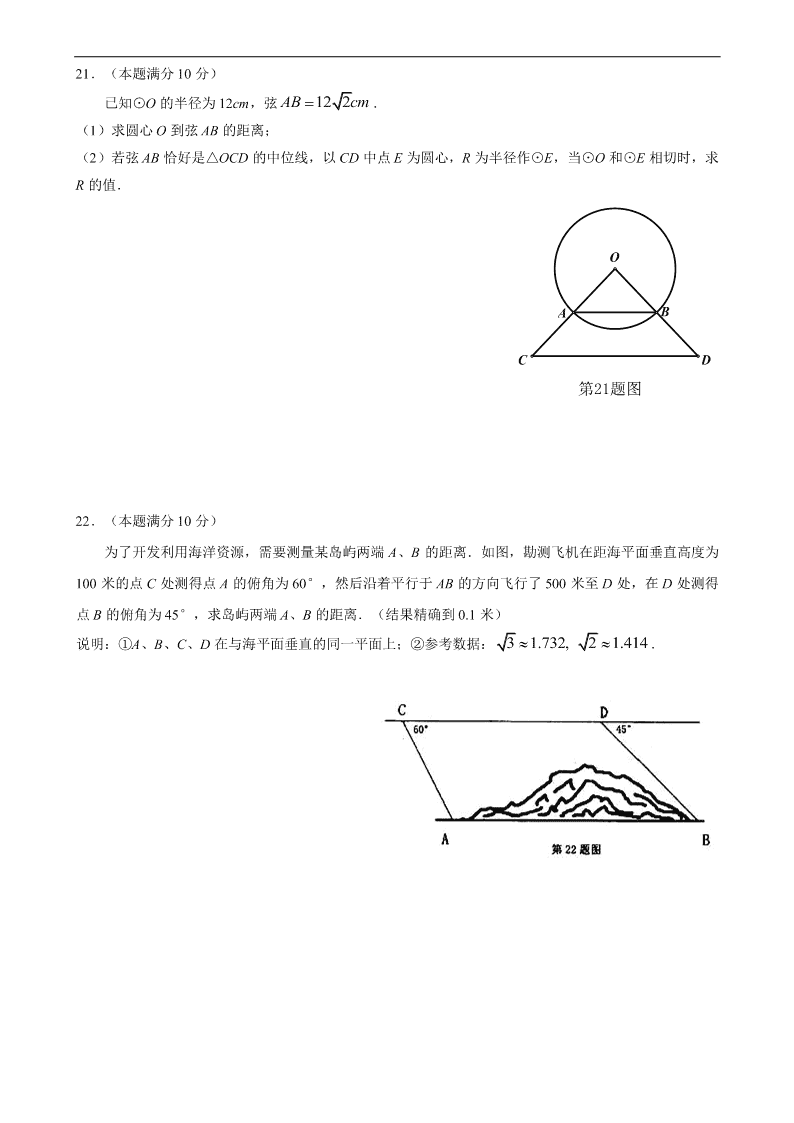第20题图 M FE A CB D 21．（本题满分 10 分） 已知⊙O 的半径为 12cm，弦 12 2AB cm ． （1）求圆心 O 到弦 AB 的距离； （2）若弦 AB 恰好是△OCD 的中位线，以 CD 中点 E 为圆心，R 为半径作⊙E，当⊙O 和⊙E 相切时，求 R 的值． 第21题图 BA DC O 22．（本题满分 10 分） 为了开发利用海洋资源，需要测量某岛屿两端 A、B 的距离．如图，勘测飞机在距海平面垂直高度为 100 米的点 C 处测得点 A 的俯角为 60°，然后沿着平行于 AB 的方向飞行了 500 米至 D 处，在 D 处测得 点 B 的俯角为 45°，求岛屿两端 A、B 的距离．（结果精确到 0.1 米） 说明：①A、B、C、D 在与海平面垂直的同一平面上；②参考数据： 3 1.732, 2 1.414． 23．（本题满分 12 分，第（1）小题满分 5 分，第（2）小题满分 7 分） 如图，△ABC 中，AC = BC，F 为底边 AB 上一点， ( , 0)BF m mnAF n，D 是 CF 中点，联结 AD 并延 长交 BC 于 E． （1）求 BE EC 的值； （2）若 BE = 2EC，求证：CF⊥AB． 第23题图 E D B A CF 24．（本题满分 12 分） 如图，在直角坐标平面上，点 A、B 在 x 轴上（A 点在 B 点左侧），点 C 在 y 轴正半轴上，若 A（– 1 , 0），OB = 3OA，且 tan∠CAO = 2． （1）求点 B、C 的坐标 （2）求经过点 A、B、C 三点的抛物线解析式； （3）P 是（2）中所求抛物线的顶点，设 Q 是此抛物线上一点，若△ABQ 与△ABP 的面积相等，求 P 点 的坐标． x y 第24题图 A O 25．（本题满分 14 分） 在△ABC 中，∠BAC = 90°，AB < AC，M 是 BC 边的中点，MN⊥BC 交 AC 于点 N．动点 P 从点 B 出发，沿射线 BA 以每秒 3 个长度单位运动，联结 MP，同时 Q 从点 N 出发，沿射线 NC 以一定的速度运 动，且始终保持 MQ⊥MP，设运动时间为 x 秒（x > 0）． （1）求证：△BMP∽△NMQ； （2）若∠B = 60°， 43AB  ，设△APQ 的面积为 y，求 y 与 x 的函数关系式； （3）判断 BP、PQ、CQ 之间的数量关系，并说明理由． 第25题图 Q N M A CB P 备用图 N M A CB 长宁区参考答案 一、选择题 1、B 2、A 3、C 4、D 5、B 6、C 二、填空题 7、2 :1 8、15 2 9、  22 1 2yx   10、4 米 11、2 12、直线 2x  13、在圆上 14、  251yx 15、1 16、1: 3 17、 3 1 2y y y 18、 3 316 三、解答题 19、原式  2013 3 3 31 3 1 1 3 1 22 2 2            20、解：∵AD＝2，BC＝3，∴ 3 2BC AD ∵AD∥BC ∴ 33 22BC AD a ∵EF 是梯形的中位线 ∴EF∥BC ∴ DM DF BM FC ∵F 是 DC 中点，即 DF＝FC ∴DM＝MB ∴FM 是△DBC 的中位线 ∴ 13 24FM BC a    . 21、解：（1）过点 O 作 AB 的垂线交 AB 于 F，交 CD 于 E ∵O 为圆心且 OF⊥AB ∴ 1 2AF BF AB ∵ 12 2AB  ∴ 62AF  在 Rt△ABC 中，OA＝12， 2 2 2AF OF OA  2 226 2 12OF ∴ 62OF  ∴圆心 O 到 AB 的距离是 62. （2）∵AB 是△OCD 的中位线 ∴AB∥CD 且 1 2 AB CD  ，∴ AFO CEO   ∵OE⊥AB 即∠AFO＝90° ∴∠CEO＝90°即 OE⊥CD ∵ ，OA＝OB＝12 ∴ 2 2 2AB OA OB ∴∠AOB＝90° ∴ OA OB OC OD ∵OA＝OB ∴OC＝OD ∴△OCD 是等腰直角三角形 ∵OE⊥CD ∴E 是 CD 中点 ∵AB∥CD，且 1 2 AB CD  ∴ 1 2 OF AB OE CD ∵ 62OF  ∴ 12 2OE  ∴外切 12 2 12OE OA R R     12 2 12R 内切 12 2 12OE R OA R     12 2 12R 22、解：作 AE⊥CD 于 E，作 BF⊥CD 于 F， 根据题意得：CD∥AB，AE＝BF＝100 米，CD＝500 米，∠ACD＝60°，∠BDF＝45° Rt△CAE 中， cot cot 60 CEACD AE    ， 3 100 57.733CE    Rt△BDF 中， tan tan 45 BFBDF DF    ， 100BF DF ∴ 500 57.73 100 542.27EF DC CE DF       ∵AE⊥CD ∴∠AEC＝90°，同理∠BFD＝90° ∴∠BFD＝∠AEC ∴AE∥BF 又∵EF∥AB ∴四边形 ABFE 是平行四边形 ∴EF＝AB ∴AB＝542.27≈542.3 ∴岛屿两端 A、B 的距离约是 542.3 米。 23、（1）解：过点 B 做 CF 的平行线与 AE 的延长线交于点 G ∵CF∥BG ∴ AF FD AB BG ∵ BF m AF n ∴ AF n AB m n  ∴ DF n BG m n  ∵D 是 CF 的中点 ∴DF＝DC ∴ DC n BG m n  ∵CF∥BG ∴ DC EC BG BE ∴ BE m n EC n  （2）∵BE＝2EC ∴ 2 mn n  则 m＝n ∴ 1BF m AF n 即 BF＝AF 又∵AC＝BC ∴CF⊥AB 24、解：（1）根据题意 OA＝1，Rt△ACO 中， tan 2OCCAO OA   ∴OC＝2 ∴  0,2C OB＝3OA＝3 ∴  3,0B （2）设     1 3 0y a x x a    代入得： 23a ∴ 2 3a  ∴    22 2 41 3 23 3 3y x x x x        （3）设  ,Q x y ∵ 224233y x x    ∴ 81, 3P  AB＝OA＋OB＝4 1 1 8 1642 2 3 3ABP pS AB y       ∵△ABQ 与△ABP 的面积相等 ∴ 1 16 23ABQS AB y    ∴ 8 3y  当 8 3y  时， 28 2 4 23 3 3xx    解得 121xx ∴ 81, 3Q  当 8 3y  时， 28 2 4 23 3 3xx     解得 1 2 2x  ∴ 81 2 2, 3Q 25、（1）∵MN⊥BC ∴∠NMB＝90°＝∠PMN＋∠BMP ∵MQ⊥MP ∴∠PMQ＝90°＝∠PMN＋∠NMQ ∴∠BMP＝∠NMQ 当点 Q 在 NC 上时，∵∠BAC＝90° ∴∠B+∠C＝90° ∵∠NMB＝90°∴∠MNC＋∠C＝90° ∴∠B＝∠MNC 在△BMP 和△NMQ 中，∠BMP＝∠NMQ 且∠B＝∠MNC ∴△BMQ∽△NMQ 当点 Q 在 NC 延长线上时，∠BMP＝∠NMB＋∠PMN＝90°＋∠PMN ∠NMQ＝∠PMQ＋∠PMN＝90°＋∠PMN ∴∠BMP＝∠NMQ 又∵∠B＝∠MNC ∴△BMP∽△NMQ （2）Rt△ABC 中，∠B＝60° 43AB  tan B 3AC AB   ∴AC＝12 ∠C＝30° 2 8 3BC AB ∵M 是 BC 的中点 ∴ 43MC BM ∵MN⊥BC ∴∠NMC＝90° Rt△MNC 中， 90 30CB     MN＝4 ∴NC＝2MN＝8 设 3BP x ， 43BM  ，由（1）知△BMP∽△NMQ ∴ BP BM NQ MN ∴NQ＝x   4AQ AN NQ AC CN NQ x       当点 P 在线段 AB 上时， 4 3 3AP x     21 1 34 3 3 4 8 3 0 4 32 2 2APQy S AP AQ x x x x          当点 P 在线段 AB 的延长线上时， 3 4 3AP x     21 1 33 4 3 4 8 3 4 32 2 2APQy S AP AQ x x x x         （3）∵  22233BP x x  2228 16 64CQ x x x        2 22 2 2 23 4 3 4 4 16 64PQ AP AQ x x x x         ∴ 2 2 2BP CQ PQ