2017浙江省湖州市中考数学试卷 17页

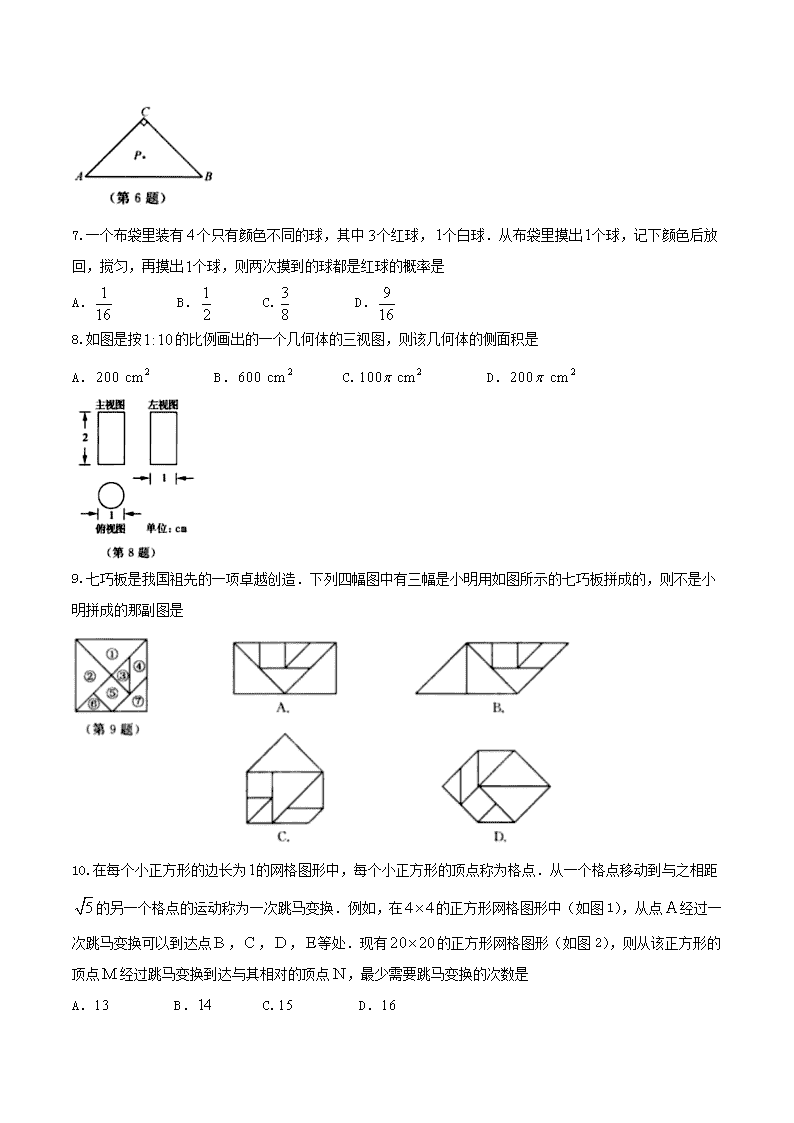
浙江省2017年初中毕业学业考试（湖州市）‎ 数学试题卷 第Ⅰ卷（共30分）‎ 一、选择题：本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.实数，，，中，无理数是 A． B． C． D．‎ ‎2.在平面直角坐标系中，点关于原点的对称点的坐标是 A． B． C． D．‎ ‎3.如图，已知在中，，，，则的值是 A． B． C． D．‎ ‎4.一元一次不等式组的解是 A． B． C. D．或 ‎5.数据，，，，，的中位数是 A． B． C. D．‎ ‎6.如图，已知在中，，，，点是的重心，则点到所在直线的距离等于 A． B． C. D．‎ ‎7.一个布袋里装有个只有颜色不同的球，其中个红球，个白球．从布袋里摸出个球，记下颜色后放回，搅匀，再摸出个球，则两次摸到的球都是红球的概率是 A． B． C. D．‎ ‎8.如图是按的比例画出的一个几何体的三视图，则该几何体的侧面积是 A． B． C. 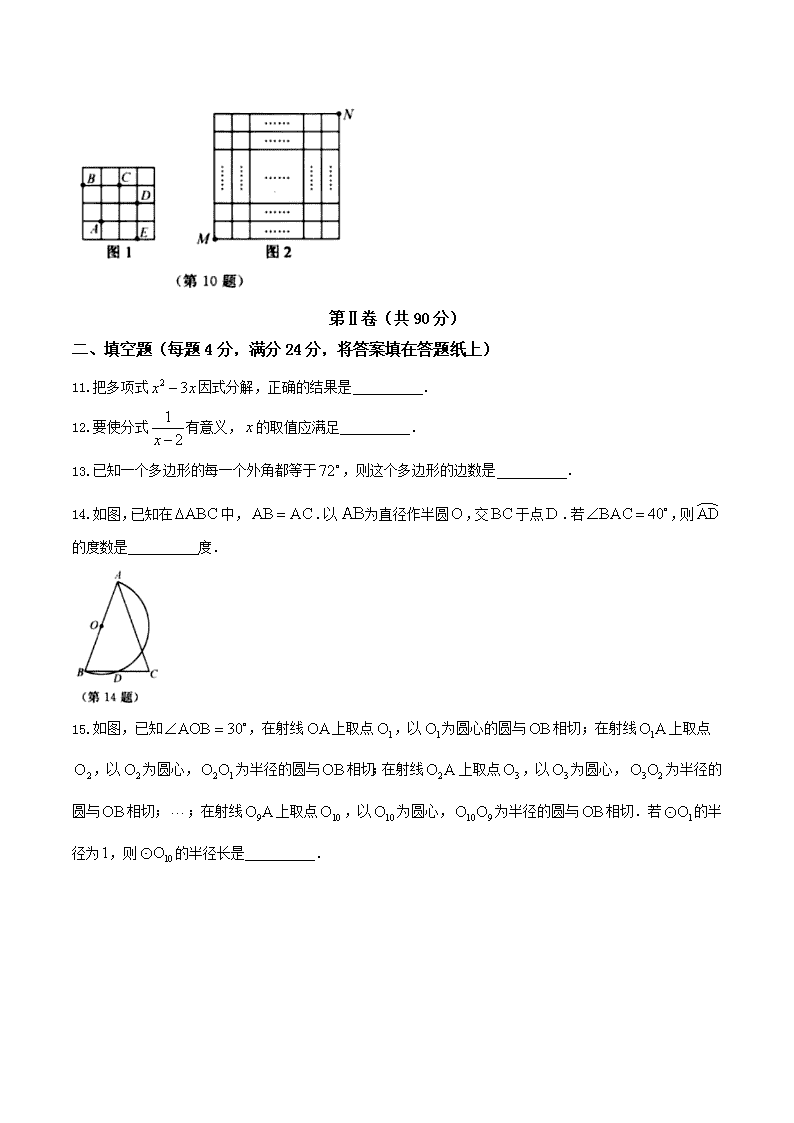D．‎ ‎9.七巧板是我国祖先的一项卓越创造．下列四幅图中有三幅是小明用如图所示的七巧板拼成的，则不是小明拼成的那副图是 ‎10.在每个小正方形的边长为的网格图形中，每个小正方形的顶点称为格点．从一个格点移动到与之相距的另一个格点的运动称为一次跳马变换．例如，在的正方形网格图形中（如图1），从点经过一次跳马变换可以到达点，，，等处．现有的正方形网格图形（如图2），则从该正方形的顶点经过跳马变换到达与其相对的顶点，最少需要跳马变换的次数是 A． B． C. D．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题4分，满分24分，将答案填在答题纸上）‎ ‎11.把多项式因式分解，正确的结果是 ．‎ ‎12.要使分式有意义，的取值应满足 ．‎ ‎13.已知一个多边形的每一个外角都等于，则这个多边形的边数是 ．‎ ‎14.如图，已知在中，．以为直径作半圆，交于点．若，则的度数是 度．‎ ‎15.如图，已知，在射线上取点，以为圆心的圆与相切；在射线上取点，以为圆心，为半径的圆与相切；在射线上取点，以为圆心，为半径的圆与相切；；在射线上取点，以为圆心，为半径的圆与相切．若的半径为，则的半径长是 ．‎ ‎16.如图，在平面直角坐标系中，已知直线（）分别交反比例函数和在第一象限的图象于点，，过点作轴于点，交的图象于点，连结．若是等腰三角形，则的值是 ．‎ 三、解答题 （本大题共8小题，共66分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. （本小题6分）‎ 计算：．‎ ‎18. （本小题6分）‎ 解方程：．‎ ‎19. （本小题6分）‎ 对于任意实数，，定义关于“”的一种运算如下：．例如：，．‎ ‎（1）若，求的值；‎ ‎（2）若，求的取值范围．‎ ‎20. （本小题8分）‎ 为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了天的调查，将所得数据绘制成如下统计图（图2不完整）：‎ 请根据所给信息，解答下列问题：‎ ‎（1）第天，这一路口的行人交通违章次数是多少次？这天中，行人交通违章次的有多少天？‎ ‎（2）请把图2中的频数直方图补充完整；（温馨提示：请画在答题卷相对应的图上）‎ ‎（3）通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章？‎ ‎21. （本小题8分）‎ 如图，为的直角边上一点，以为半径的与斜边相切于点，交于点．已知，．‎ ‎（1）求的长；‎ ‎（2）求图中阴影部分的面积．‎ ‎22. （本小题10分）‎ 已知正方形的对角线，相交于点．‎ ‎（1）如图1，，分别是，上的点，与的延长线相交于点．若，求证：；‎ ‎（2）如图2，是上的点，过点作，交线段于点，连结交于点，交于点．若，‎ ①求证：；‎ ②当时，求的长．‎ ‎23. （本小题10分）‎ 湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养天的总成本为万元；放养天的总成本为万元（总成本=放养总费用+收购成本）．‎ ‎（1）设每天的放养费用是万元，收购成本为万元，求和的值；‎ ‎（2）设这批淡水鱼放养天后的质量为（），销售单价为元/．根据以往经验可知：与的函数关系为；与的函数关系如图所示．‎ ①分别求出当和时，与的函数关系式；‎ ②设将这批淡水鱼放养天后一次性出售所得利润为元，求当为何值时，最大？并求出最大值．（利润=销售总额-总成本）‎ ‎24. （本小题12分）‎ 如图，在平面直角坐标系中，已知，两点的坐标分别为，，是线段上一点（与，点不重合），抛物线（）经过点，，顶点为，抛物线（）经过点，，顶点为，，的延长线相交于点．‎ ‎（1）若，，求抛物线，的解析式；‎ ‎（2）若，，求的值；‎ ‎（3）是否存在这样的实数（），无论取何值，直线与都不可能互相垂直？若存在，请直接写出的两个不同的值；若不存在，请说明理由．‎