2005年上海市中考数学试题及答案 9页

2005 年上海市中考数学试卷 一. 填空题（本大题共 14 题，满分 42 分） 只要求直接填写结果，每个空格填对得 3 分，否则得零分。 1. 计算： ( )x2 2  _____________。 2. 分解因式： a a2 2  ____________。 3. 计算：  2 1 2 1   ____________。 4. 函数 y x 的定义域是_________________。 5. 如果函数 f x x( )  1，那么 f ( )1  ___________。 6. 点 A( )2 4， 在正比例函数的图像上，这个正比例函数的解析式是______________。 7. 如果将二次函数 y x 2 2 的图像沿 y 轴向上平移 1 个单位，那么所得图像的函数解析 式是___________________。 8. 已知一元二次方程有一个根为 1，那么这个方程可以是_________________（只需写出 一个方程）。 9. 如果关于 x 的方程 x x a2 4 0   有两个相等的实数根，那么 a=__________。 10. 一个梯形的两底长分别为 6 和 8，这个梯形的中位线长为____________。 11. 在△ABC 中，点 D、E 分别在边 AB 和 AC 上，且 DE//BC，如果 AD=2，DB=4，AE=3， 那么 EC=__________________。 12. 如图所示，自动扶梯 AB 段的长度为 20 米，倾斜角 A 为α ，高度 BC 为___________ 米（结果用含α 的三角比表示）。 13. 如果半径分别为 2 和 3 的两个圆外切，那么这两个圆的圆心距是______________。 14. 在三角形纸片 ABC 中，    C A AC90 30 3°， °， ，折叠该纸片，使点 A 与点 B 重合，折痕与 AB、AC 分别相交于点 D 和点 E（如图所示）。折痕 DE 的长为 ____________________。 二. 选择题（本大题共 4 题，满分 12 分） 下列各题的四个结论中，有且只有一个结论是正确的，把正确结论的代号写在题后的 圆括号内，选对得 3 分；不选、错选或者多选得零分。 15. 在下列实数中，是无理数的为（ ） A. 0 B. 35. C. 2 D. 9 16. 六个学生进行投篮比赛，投进的个数分别为 2，3，3，5，10，13，这六个数的中位 数是（ ） A. 3 B. 4 C. 5 D. 6 17. 已知 Rt ABC 中，    C AC BC90 2 3°， ， ，那么下列各式中，正确的是 （ ） A. sin B  2 3 B. cosB  2 3 C. tgB  2 3 D. ctgB  2 3 18. 在下列命题中，真命题是（ ） A. 两个钝角三角形一定相似 B. 两个等腰三角形一定相似 C. 两个直角三角形一定相似 D. 两个等边三角形一定相似 三. 解答题（本大题共 3 题，满分 24 分） 19. （本题满分 8 分） 解不等式组： 3 1 5 2 1 6 x x x x          ( ) ，并把解集在数轴上表示出来。 20. （本题满分 8 分） 解方程： x x x x x     2 2 2 8 42 21. 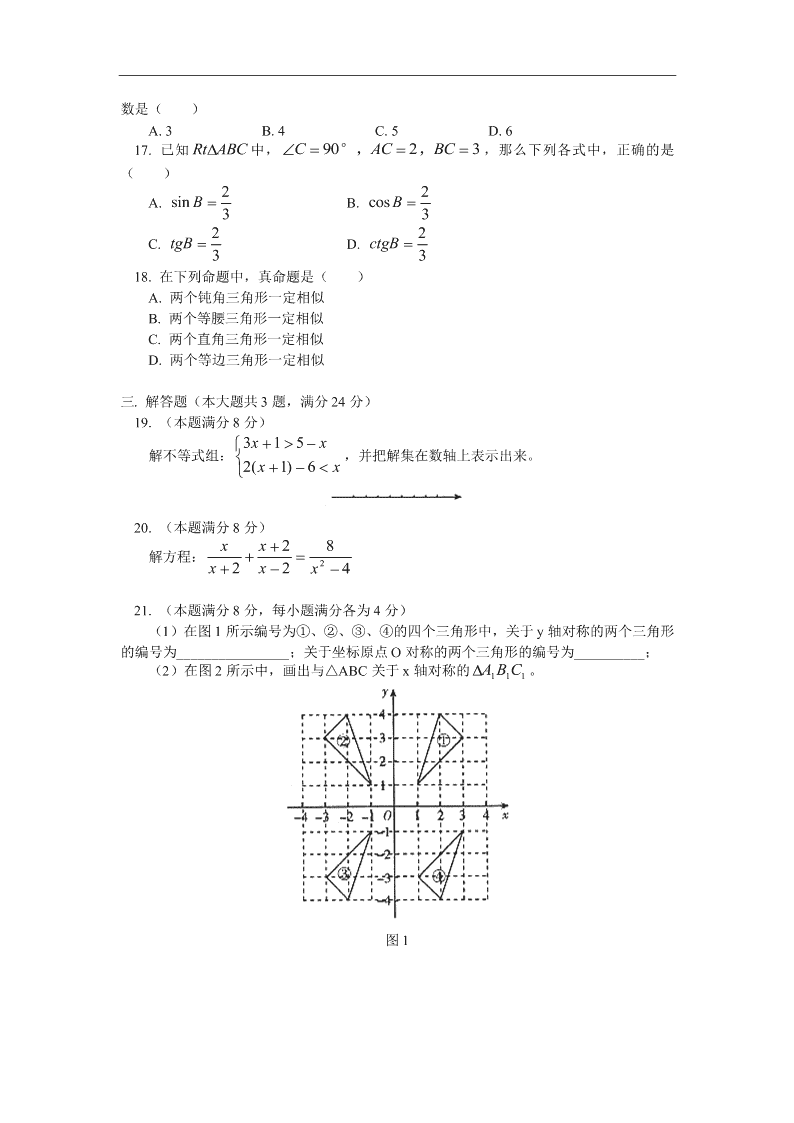（本题满分 8 分，每小题满分各为 4 分） （1）在图 1 所示编号为①、②、③、④的四个三角形中，关于 y 轴对称的两个三角形 的编号为________________；关于坐标原点 O 对称的两个三角形的编号为__________； （2）在图 2 所示中，画出与△ABC 关于 x 轴对称的 A B C1 1 1 。 图 1 图 2 四. 证明题（本大题共 4 题，满分 42 分） 22. 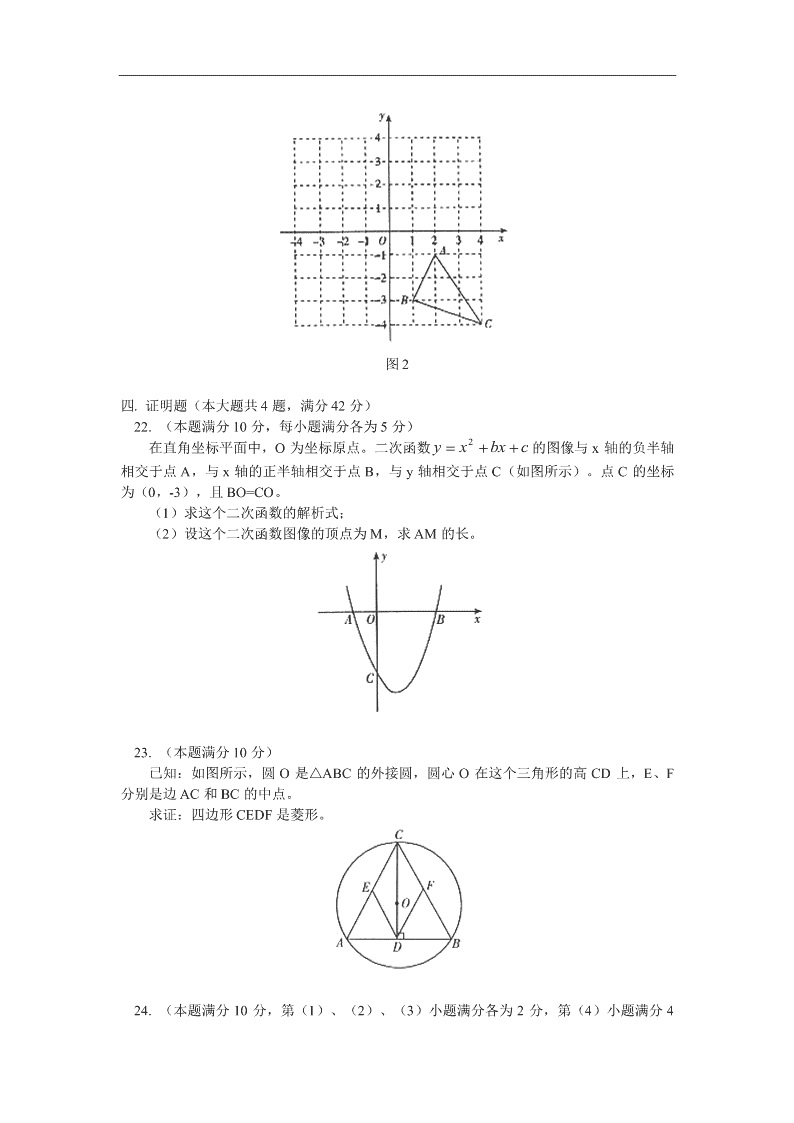（本题满分 10 分，每小题满分各为 5 分） 在直角坐标平面中，O 为坐标原点。二次函数 y x bx c  2 的图像与 x 轴的负半轴 相交于点 A，与 x 轴的正半轴相交于点 B，与 y 轴相交于点 C（如图所示）。点 C 的坐标 为（0，-3），且 BO=CO。 （1）求这个二次函数的解析式； （2）设这个二次函数图像的顶点为 M，求 AM 的长。 23. （本题满分 10 分） 已知：如图所示，圆 O 是△ABC 的外接圆，圆心 O 在这个三角形的高 CD 上，E、F 分别是边 AC 和 BC 的中点。 求证：四边形 CEDF 是菱形。 24. （本题满分 10 分，第（1）、（2）、（3）小题满分各为 2 分，第（4）小题满分 4 分） 小明家使用的是分时电表，按平时段（6：00~22：00）和谷时段（22：00~次日 6：00） 分别计费。平时段每度电价为 0.61 元，谷时段每度电价为 0.30 元。小明将家里 2005 年 1 月至 5 月的平时段和谷时段的月用电量分别用折线图表示（如图所示），同时将前 4 个月 的月用电量和相应电费制成表格（如表 1）。 表 1 项目 月份 月用电量 （度） 电费（元） 1 月 90 51.80 2 月 92 50.85 3 月 98 49.24 4 月 105 48.55 5 月 根据上述信息，解答下列问题： （1）计算 5 月份的月用电量及相应电费，将所得结果填入表 1 中； （2）小明家这 5 个月的月平均用电量为____________度； （3）小明家这 5 个月每月用电量呈________________趋势（选择“上升”或“下降”）； 这 5 个月每月电费呈______________趋势（选择“上升”或“下降”）； （4）小明预计 7 月份家中用电量很大，估计 7 月份用电量可达 500 度，相应电费将达 243 元。请你根据小明的估计，计算出 7 月份小明家平时段用电量和谷时段用电量。 25. （本题满分 12 分，每小题满分各为 4 分） 在△ABC 中，   ABC AB BC90 4 3°， ， 。O 是边 AC 上的一个动点，以点 O 为圆心作半圆，与边 AB 相切于点 D，交线段 OC 于点 E，作 EP ED ，交射线 AB 于点 P， 交射线 CB 于点 F。 （1）如图 1 所示，求证：  ADE AEP ； （2）设 OA=x，AP=y，求 y 关于 x 的函数解析式，并写出它的定义域； （3）当 BF=1 时，求线段 AP 的长。 图 1 图 2 参考答案 一. 填空题 1. x 4 2. a a( ) 2 3. 1 4. x  0 5. 2 6. y x 2 7. y x 2 12 8. x x2 0  等 9. 4 10. 7 11. 6 12. 20sin 13. 5 14. 1 二. 选择题 15. C 16. B 17. C 18. D 三. 解答题 19. 由 3 1 5 1x x x   ，得 由 2 1 6( )x x   ，得 x  4 ∴不等式组的解集为1 4 x 解集在数轴上表示正确。 20. 解：去分母，得 x x x( ) ( )   2 2 82 x x x x2 22 4 4 8     整理，得： x x2 2 0   解得： x x1 22 1  ， 经检验， x1 1 为原方程的根， x2 2  是增根 ∴原方程的根是 x  1 21. （1）①和② ①和③ （2）所画三角形正确。 四. 解答题 22. 解：（1）∵BO=CO，点 C 的坐标为（0，-3），点 B 在 x 轴的正半轴上 ∴点 B 的坐标为（3，0） ∵点 C、点 B 在二次函数 y x bx c  2 的图像上         c b c 3 3 3 02 解得： c b        3 2 ∴二次函数的解析式为 y x x  2 2 3 （2） y x x x     2 22 3 1 4( ) ∴点 M 的坐标为（1，-4） 又∵二次函数 的图像与 x 轴的负半轴相交于点 A ∴点 A 的坐标为（1，-4） 又∵二次函数 y x x  2 2 3的图像与 x 轴的负半轴相交于点 A ∴点 A 的坐标为（-1，0）       AM ( ) ( )1 1 4 0 2 52 2 23. 证法一：∵O 为圆心，AB 为圆 O 的弦， OD AB  AD BD 又CD AB AC BC  ，             CDA E AC DE AC EC DF BC CF DE EC CF FD CEDF 90 1 2 1 2 °， 是 的中点 同理 四边形 是菱形 证法二：∵O 为圆心，AB 为圆 O 的弦， ∵D、F 分别为 AB、BC 的中点  FD AC FD AC/ / ，且 1 2   E AC EC AC FD CEDF CDA E AC DE AC EC CEDF 是 的中点 四边形 是平行四边形 °， 是 的中点 四边形 是菱形           1 2 90 1 2 证法三：连结 EF，交 CD 于点 G E F AC BC、 分别为 、 的中点             EF AB CG DG EG AD CG CD GF DB O AB O OD AB AD BD EG GF CG DG EG GF / / ， 为圆心， 为圆 的弦， ，   ∴四边形 CEDF 是平行四边形 EF AB CD AB CD EF / / ，    ∴四边形 CEDF 是菱形 24. （1）110 46.95 （2）99 （3）上升 下降 （4）解：设小明家 7 月份平时段用电量为 x 度，谷时段用电量为 y 度 根据题意，得 x y x y        500 061 030 243. . 解得： x y      300 200 答：小明家 7 月份平时段用电量为 300 度，谷时段用电量为 200 度。 25. （1）证明：如图 1 所示，连结 OD 根据题意，得 OD AB ，即  ODA 90°    OE OD ODE OED DEP ADE AEP A A ADE AEP               90° 又   （2）解：   ABC AB BC90 4 3°， ，  AC 5 OA x OE OD x AD x AE x x x          ， ，3 5 4 5 3 5 8 5 当点 O 在边 AC 上移动时，总有  ADE AEP          AP AE AE AD y x x16 5 0 25 8 （3）解法一： ADE AEP            AE AD PE ED AE x AD x PE ED AE AD BPF EPD BP BF PE ED  8 5 4 5 2 2 ， 易证 ，    当 时，BF BP1 2 ①若 EP 交线段 CB 的延长线于点 F（如图 1 所示），则 AP BP  4 2 图 1 ②若 EP 交线段 CB 于点 F（如图 2 所示），则 AP BP  4 6 图 2 解法二：当 BF=1 时 ①若 EP 交线段 CB 的延长线于点 F（如图 1 所示），则 CF=4                              ADE AEP PDE PEC FBP DEP FPB DPE F PDE CFE FEC CF CE CE AE x x x x y AP 90 5 5 8 5 8 5 4 5 8 2 2 °， ，得 ，即 ②若 EP 交线段 CB 于点 F（如图 2 所示），则 CF=2 类似①，易得 CF CE CE AE x x x y AP            5 5 8 5 5 8 5 2 15 8 6 6 ，得 ，即