2019年湖南省张家界市中考数学试卷 25页

2019 年湖南省张家界市中考数学试卷 一、选择题（本大题共 8 个小题，每小题 3 分，满分 24 分，在每小题给出的四个选项中， 只有一项是符合题目要求的） 1．（3 分）2019 的相反数是（ ） A．2019 B．﹣2019 C． D．﹣ 2．（3 分）为了有力回击美方单边主义贸易政策的霸凌行为，维护我国正当权益和世界多边 贸易正常秩序，经国务院批准，决定于 2019 年 6 月 1 日起，对原产于美国的 600 亿美元 进口商品加征关税，其中 600 亿美元用科学记数法表示为（ ）美元． A．6×1010 B．0.6×1010 C．6×109 D． 0.6×109 3．（3 分）下列四个立体图形中，其主视图是轴对称图形但不是中心对称图形的是（ ） A． B． C． D． 4．（3 分）下列运算正确的是（ ） A．a2•a3＝a6 B．a2+a3＝a5 C．（a+b）2＝a2+b2 D．（a3）2＝a6 5．（3 分）下列说法正确的是（ ） A．打开电视机，正在播放“张家界新闻”是必然事件 B．天气预报说“明天的降水概率为 65%”，意味着明天一定下雨 C．两组数据平均数相同，则方差大的更稳定 D．数据 5，6，7，7，8 的中位数与众数均为 7 6．（3 分）不等式组 的解集在数轴上表示为（ ） A． B． C． D． 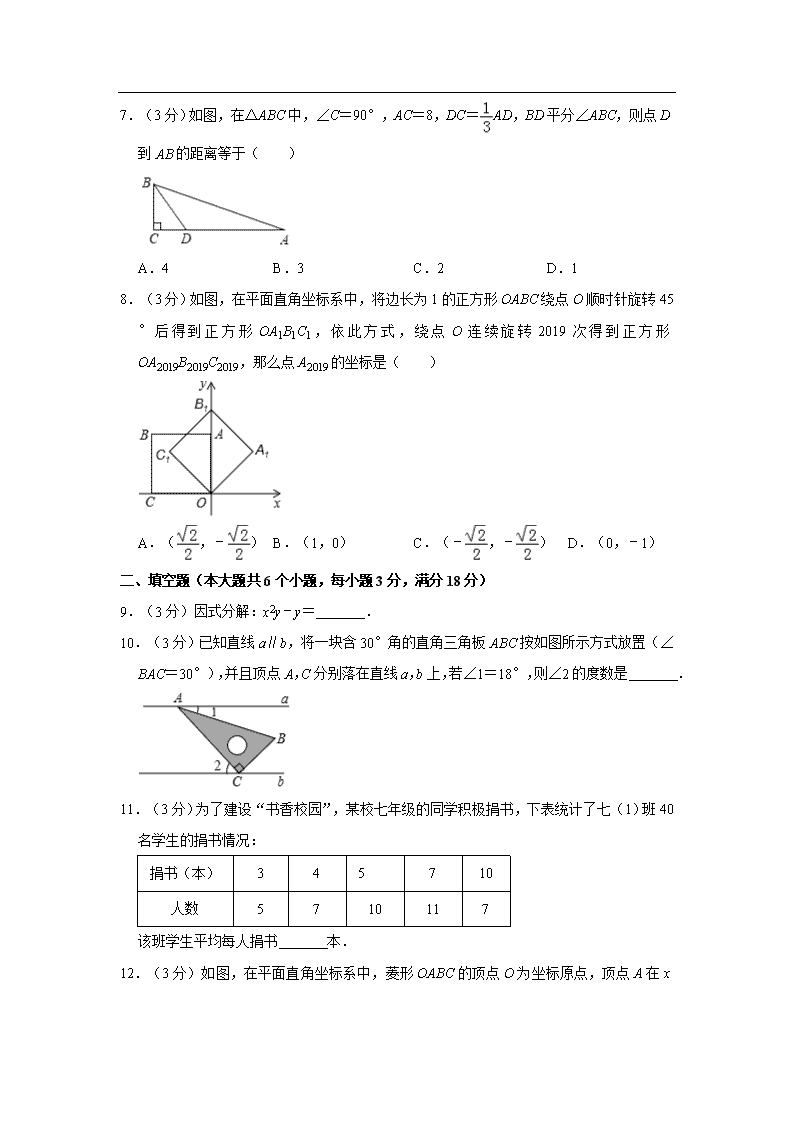7．（3 分）如图，在△ABC 中，∠C＝90°，AC＝8，DC＝ AD，BD 平分∠ABC，则点 D 到 AB 的距离等于（ ） A．4 B．3 C．2 D．1 8．（3 分）如图，在平面直角坐标系中，将边长为 1 的正方形 OABC 绕点 O 顺时针旋转 45 ° 后 得 到 正 方 形 OA1B1C1 ， 依 此 方 式 ， 绕 点 O 连 续 旋 转 2019 次 得 到 正 方 形 OA2019B2019C2019，那么点 A2019 的坐标是（ ） A．（ ，﹣ ） B．（1，0） C．（﹣ ，﹣ ）D．（0，﹣1） 二、填空题（本大题共 6 个小题，每小题 3 分，满分 18 分） 9．（3 分）因式分解：x2y﹣y＝ ． 10．（3 分）已知直线 a∥b，将一块含 30°角的直角三角板 ABC 按如图所示方式放置（∠ BAC＝30°），并且顶点 A，C 分别落在直线 a，b 上，若∠1＝18°，则∠2 的度数是 ． 11．（3 分）为了建设“书香校园”，某校七年级的同学积极捐书，下表统计了七（1）班 40 名学生的捐书情况： 捐书（本） 3 4 5[来源:学|科|网 Z|X|X|K] 7 10 人数 5 7 10 11 7 该班学生平均每人捐书 本． 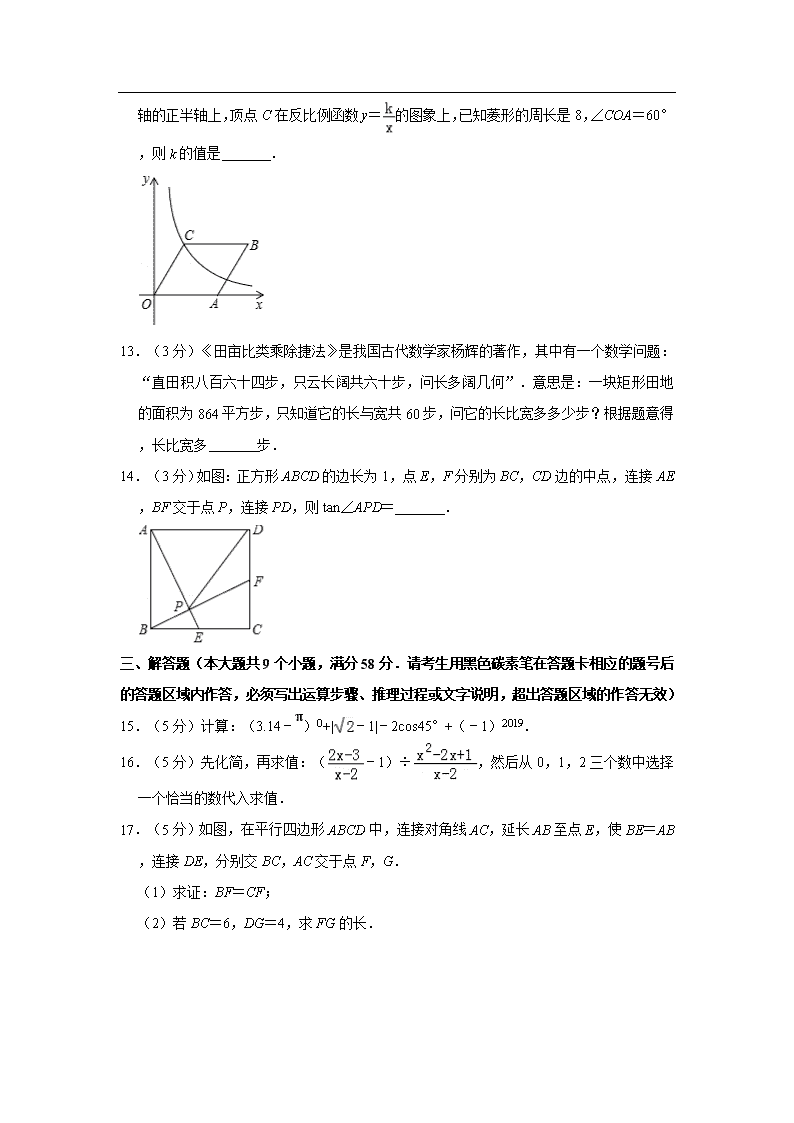12．（3 分）如图，在平面直角坐标系中，菱形 OABC 的顶点 O 为坐标原点，顶点 A 在 x 轴 的正半轴上，顶点 C 在反比例函数 y＝ 的图象上，已知菱形的周长是 8，∠COA＝60 °，则 k 的值是 ． 13．（3 分）《田亩比类乘除捷法》是我国古代数学家杨辉的著作，其中有一个数学问题：“直 田积八百六十四步，只云长阔共六十步，问长多阔几何”．意思是：一块矩形田地的面积 为 864 平方步，只知道它的长与宽共 60 步，问它的长比宽多多少步？根据题意得，长比 宽多 步． 14．（3 分）如图：正方形 ABCD 的边长为 1，点 E，F 分别为 BC，CD 边的中点，连接 AE， BF 交于点 P，连接 PD，则 tan∠APD＝ ． 三、解答题（本大题共 9 个小题，满分 58 分．请考生用黑色碳素笔在答题卡相应的题号后 的答题区域内作答，必须写出运算步骤、推理过程或文字说明，超出答题区域的作答无效） 15．（5 分）计算：（3.14﹣ π ）0+| ﹣1|﹣2cos45°+（﹣1）2019． 16．（5 分）先化简，再求值：（ ﹣1）÷ ，然后从 0，1，2 三个数中选择一 个恰当的数代入求值． 17．（5 分）如图，在平行四边形 ABCD 中，连接对角线 AC，延长 AB 至点 E，使 BE＝AB， 连接 DE，分别交 BC，AC 交于点 F，G． （1）求证：BF＝CF； （2）若 BC＝6，DG＝4，求 FG 的长． 18．（6 分）某社区购买甲、乙两种树苗进行绿化，已知甲种树苗每棵 30 元，乙种树苗每棵 20 元，且乙种树苗棵数比甲种树苗棵数的 2 倍少 40 棵，购买两种树苗的总金额为 9000 元． （1）求购买甲、乙两种树苗各多少棵？ （2）为保证绿化效果，社区决定再购买甲、乙两种树苗共 10 棵，总费用不超过 230 元， 求可能的购买方案？ 19．（6 分）阅读下面的材料： 按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项．排在第 一位的数称为第一项，记为 a1，排在第二位的数称为第二项，记为 a2，依此类推，排在 第 n 位的数称为第 n 项，记为 an．所以，数列的一般形式可以写成：a1，a2，a3，…，an，…． 一般地，如果一个数列从第二项起，每一项与它前一项的差等于同一个常数，那么这个 数列叫做等差数列，这个常数叫做等差数列的公差，公差通常用 d 表示．如：数列 1，3， 5，7，…为等差数列，其中 a1＝1，a2＝3，公差为 d＝2． 根据以上材料，解答下列问题： （1）等差数列 5，10，15，…的公差 d 为 ，第 5 项是 ． （2）如果一个数列 a1，a2，a3，…，an…，是等差数列，且公差为 d，那么根据定义可 得到：a2﹣a1＝d，a3﹣a2＝d，a4﹣a3＝d，…，an﹣an﹣1＝d，…． 所以 a2＝a1+d a3＝a2+d＝（a1+d）+d＝a1+2d，[来源:学科网] a4＝a3+d＝（a1+2d）+d＝a1+3d， …… 由此，请你填空完成等差数列的通项公式：an＝a1+（ ）d． （3）﹣4041 是不是等差数列﹣5，﹣7，﹣9…的项？如果是，是第几项？ 20．（6 分）天门山索道是世界最长的高山客运索道，位于张家界天门山景区．在一次检修 维护中，检修人员从索道 A 处开始，沿 A﹣B﹣C 路线对索道进行检修维护．如图：已知 AB＝500 米，BC＝800 米，AB 与水平线 AA1 的夹角是 30°，BC 与水平线 BB1 的夹角是 60°．求：本次检修中，检修人员上升的垂直高度 CA1 是多少米？（结果精确到 1 米， 参考数据： ≈1.732） 21．（7 分）如图，AB 为 ⊙ O 的直径，且 AB＝4 ，点 C 是 上的一动点（不与 A，B 重 合），过点 B 作 ⊙ O 的切线交 AC 的延长线于点 D，点 E 是 BD 的中点，连接 EC． （1）求证：EC 是 ⊙ O 的切线； （2）当∠D＝30°时，求阴影部分面积． 22．（8 分）为了响应市政府号召，某校开展了“六城同创与我同行”活动周，活动周设置 了“A：文明礼仪，B：生态环境，C：交通安全，D：卫生保洁”四个主题，每个学生选 一个主题参与．为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查 结果绘制了如下条形统计图和扇形统计图． （1）本次随机调查的学生人数是 人； （2）请你补全条形统计图； （3）在扇形统计图中，“B”所在扇形的圆心角等于 度； （4）小明和小华各自随 机参加其中的一个主题活动，请用画树状图或列表的方式求他们 恰好选中同一个主题活动的概率． 23．（10 分）已知抛物线 y＝ax2+bx+c（a≠0）过点 A（1，0），B（3，0）两点，与 y 轴交 于点 C，OC＝3． （1）求抛物线的解析式及顶点 D 的坐标； （2）过点 A 作 AM⊥BC，垂足为 M，求证：四边形 ADBM 为正方形； （3）点 P 为抛物线在直线 BC 下方图形上的一动点，当△PBC 面积最大时，求点 P 的坐 标； （4）若点 Q 为线段 OC 上的一动点，问：AQ+ QC 是否存在最小值？若存在，求岀这 个最小值；若不存在，请说明理由． 2019 年湖南省张家界市中考数学试卷 参考答案与试题解析 一、选择题（本大题共 8 个小题，每小题 3 分，满分 24 分，在每小题给出的四个选项中， 只有一项是符合题目要求的） 1．（3 分）2019 的相反数是（ ） A．2019 B．﹣2019 C． D．﹣ 【考点】14：相反数． 菁优网版 权所有 【分析】由相反数的定义即可得到答案． 【解答】解：2019 的相反数是﹣2019． 故选：B． 【点评】本题运用了相反数的知识点，准确掌握定义是解题的关键． 2．（3 分）为了有力回击美方单边主义贸易政策的霸凌行为，维护我国正当权益和世界多边 贸易正常秩序，经国务院批准，决定于 2019 年 6 月 1 日起，对原产于美国的 600 亿美元 进口商品加征关税，其中 600 亿美元用科学记数法表示为（ ）美元． A．6×1010 B．0.6×1010 C．6×109 D．0.6×109 【考点】1I：科学记数法—表示较大的数．菁优网版 权所有 【分析】运用科学记数法的知识可解． 【解答】解：600 亿＝6×1010． 故选：A． 【点评】本题运用了科学记数法的知识点，掌握好 n 与数位之间的关系是解此题的关键． 3．（3 分）下列四个立体图形中，其主视图是轴对称图形但不是中心对称图形的是（ ） A． B． C． D． 【考点】P3：轴对称图形；R5：中心对称图形；U1：简单几何体的三视图． 菁优网版 权所有 【分析】根据从正面看得到的图形是主视图以及轴对称图形、中心对称图形的概念，可 得答案． 【解答】解：A、是轴对称图形，也是中心对称图形．故错误； B、是轴对称图形，也是中心对称图形．故错误； C、是轴对称图形，不是中心对称图形．故正确； D、是轴对称图形，也是中心对称图形．故错误． 故选：C． 【点评】本题考查了几何体的三视图以及中心对称图形与轴对称图形的概念：轴对称图 形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对 称中心，旋转 180 度后与原图重合． 4．（3 分）下列运算正确的是（ ） A．a2•a3＝a6 B．a2+a3＝a5 C．（a+b）2＝a2+b2 D．（a3）2＝a6 【考点】35：合并同类项；46：同底数幂的乘法；47：幂的乘方与积的乘方；4C：完全 平方公式．菁优网版 权所有 【分析】根据同底数幂的乘法法则，完全平方公式，幂的乘方公式进行运算即可； 【解答】解：a2•a3＝a2+3＝a5；A 错误； a2+a3＝a2+a3；B 错误； （a+b）2＝a2+b2+2ab；C 错误； （a3）2＝a3×2＝a6；D 正确； 故选：D． 【点评】本题考查整式的运算；熟练掌握同底数 幂的乘法，幂的乘方和积的乘方，完全 平方公式是解题的关键． 5．（3 分）下列说法正确的是（ ）[来源:学科网 ZXXK] A．打开电视机，正在播放“张家界新闻”是必然事件 B．天气预报说“明天的降水概率为 65%”，意味着明天一定下雨 C．两组数据平均数相同，则方差大的更稳定 D．数据 5，6，7，7，8 的中位数与众数均为 7 【考点】W1：算术平均数；W4：中位数；W5：众数；W7：方差；X1：随机事件；X3： 概率的意义． 菁优网版 权所有 【分析】事件发生的可能性越大，概率越接近与 1，事件发生的可能性越小，概率越接近 于 0．事件发生的可能性越大，概率越接近与 1，事件发生的可能性越小，概率越接近于 0． 【解答】解：A．打开电视机，正在播放“张家界新闻”是随机事件，故 A 错误； B．天气 预报说“明天的降水概率为 65%”，意味着明天可能下雨，故 B 错误； C．两组数据平均数相同，则方差大的更不稳定，故 C 错误； D，数据 5，6，7，7，8 的中位数与众数均为 7，正确． 故选：D．[来源:学科网 ZXXK] 【点评】本题考查了概率及其应用，正确理解概率的意义是解题的关键． 6．（3 分）不等式组 的解集在数轴上表示为（ ） A． B． C． D． 【考点】C4：在数轴上表示不等式的解集；CB：解一元一次不等式组． 菁优网版 权所有 【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中 间找、大大小小无解了确定不等式组的解集． 【解答】解：解不等式 2x﹣2≤0，得：x≤1， 则不等式组的解集为﹣1＜x≤1， 故选：B． 【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知 “同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键． 7．（3 分）如图，在△ABC 中，∠C＝90°，AC＝8，DC＝ AD，BD 平分∠ABC，则点 D 到 AB 的距离等于（ ） A．4 B．3 C．2 D．1 【考点】KF：角平分线的性质． 菁优网版 权所有 【分析】过点 D 作 DE⊥AB 于 E，求出 CD，再根据角平分线上的点到角的两边的距离 相等解答． 【解答】解：如图，过点 D 作 DE⊥AB 于 E， ∵AC＝8，DC＝ AD， ∴CD＝8× ＝2， ∵∠C＝90°，BD 平分∠ABC， ∴DE＝CD＝2， 即点 D 到 AB 的距离为 2． 故选：C． 【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的 关键． 8．（3 分）如图，在平面直角坐标系中，将边长为 1 的正方形 OABC 绕点 O 顺时针旋转 45 ° 后 得 到 正 方 形 OA1B1C1 ， 依 此 方 式 ， 绕 点 O 连 续 旋 转 2019 次 得 到 正 方 形 OA2019B2019C2019，那么点 A2019 的坐标是（ ） A．（ ，﹣ ） B．（1，0） C．（﹣ ，﹣ ）D．（0，﹣1） 【考点】D2：规律型：点的坐标；R7：坐标与图形变化﹣旋转． 菁优网版 权所有 【分析】探究规律，利用规律解决问题即可． 【解答】解：∵四边形 OABC 是正方形，且 OA＝1， ∴A（0，1）， ∵将正方形 OABC 绕点 O 逆时针旋转 45°后得到正方形 OA1B1C1， ∴A1（ ， ），A2（1，0），A3（ ，﹣ ），…， 发现是 8 次一循环，所以 2019÷8＝252…余 3， ∴点 A2019 的坐标为（ ，﹣ ） 故选：A． 【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所 连线段的夹角等于旋转角．也考查了坐标与图形的变化、规律型：点的坐标等知识，解 题的关键是学会从特殊到一般的探究规律的方法，属于中考常考题型． 二、填空题（本大题共 6 个小题，每小题 3 分，满分 18 分） 9．（3 分）因式分解：x2y﹣y＝ y（x+1）（x﹣1） ． 【考点】55：提公因式法与公式法的综合运用． 菁优网版 权所有 【分析】首先提公因式 y，再利用平方差进行二次分解即可． 【解答】解：原式＝y（x2﹣1）＝y（x+1）（x﹣1）， 故答案为：y（x+1）（x﹣1）． 【点评】此题主要考查了提公因式法和公式法分解因式，关键是掌握提取公因式后利用 平方差公式进行二次分解，注意分解要彻底． 10．（3 分）已知直线 a∥b，将一块含 30°角的直角三角板 ABC 按如图所示方式放置（∠ BAC＝30°），并且顶点 A，C 分别落在直线 a，b 上，若∠1＝18°，则∠2 的度数是 48 ° ． 【考点】JA：平行线的性质． 菁优网版 权所有 【分析】根据平行线的性质和直角三角形的性质解答即可． 【解答】解：∵a∥b， ∴∠2＝∠1+∠CAB＝18°+30°＝48°， 故答案为：48° 【点评】此题考查平行线的性质，关键是根据平行线的性质和直角三角形的性质解答． 11．（3 分）为了建设“书香校园”，某校七年级的同学积极捐书，下表统计了七（1）班 40 名学生的捐书情况： 捐书（本） 3 4[来源:Zxxk.Com] 5 7 10 人数 5 7 10 11 7 该班学生平均每人捐书 6 本． 【考点】W2：加权平均数．菁优网版 权所有 【分析】根据加权平均数的定义计算可得． 【解答】解：该班学生平均每人捐书 ＝6（本）， 故答案为：6． 【点评】本题主要考查加权平均数，解题的关键是掌握加权平均数的定义． 12．（3 分）如图，在平面直角坐标系中，菱形 OABC 的顶点 O 为坐标原点，顶点 A 在 x 轴 的正半轴上，顶点 C 在反比例函数 y＝ 的图象上，已知菱形的周长是 8，∠ COA＝60 °，则 k 的值是 ． 【考点】G6：反比例函数图象上点的坐标特征；KM：等边三角形的判定与性质；L8： 菱形的性质． 菁优网版 权所有 【分析】菱形 OABC 的周长为 8，可得边长为 2，过 C 作 x 轴的垂线，构造直角三角形， 利用 30°角所对的直角边等于斜边的一半和勾股定理，可以求出表示 C 点坐标的线段的 长，从而确定点 C 的坐标，再依据点 C 在反比例函数的图象上，代入关系式可以求出 k 的值． 【解答】解：过点 C 作 CD⊥OA，垂足为 D， ∵∠COA＝60° ∴∠OCD＝90°﹣60°＝30° 又∵菱形 OABC 的周长是 8， ∴OC＝OA＝AB＝BC＝2， 在 Rt△COD 中，OD＝ OC＝1， ∴CD＝ ， ∴C（1， ）， 把 C（1， ）代入反比例函数 y＝ 得：k＝1× ＝ ， 故答案为： ． 【点评】此题综合利用直角三角形中 30°角所对的直角边等于斜边的一半，勾股定理、 菱形的性质以及反比例函数图象上的点的坐标特征等知识，难度不大，但考查的知识较 多． 13．（3 分）《田亩比类乘除捷法》是我国古代数学家杨辉的著作，其中有一个数学问题：“直 田积八百六十四步，只云长阔共六十步，问长多阔几何”．意思是：一块矩形田地的面积 为 864 平方步，只知道它的长与宽共 60 步，问它的长比宽多多少步？根据题意得，长比 宽多 12 步． 【考点】1O：数学常识；AD：一元二次方程的应用．菁优网版 权所有 【分析】根据题意，可以列出相应的一元二次方程，从而可以解答本题． 【解答】解：设长为 x 步，宽为（60﹣x）步， x（60﹣x）＝864， 解得，x1＝36，x2＝24（舍去）， ∴当 x＝36 时，60﹣x＝24， ∴长比宽多：36﹣24＝12（步）， 故答案为：12． 【点评】本题考查一元二次方程的应用，解答本题的关键是明确题意，列出相应的方程， 利用方程的知识解答，注意长比宽要长． 14．（3 分）如图：正方形 ABCD 的边长为 1，点 E，F 分别为 BC，CD 边的中点，连接 AE， BF 交于点 P，连接 PD，则 tan∠APD＝ 2 ． 【考点】KD：全等三角形的判定与性质；LE：正方形的性质；T7：解直角三角形． 菁优网版 权所有 【分析】首先证明△ABE≌△BCF，再利用角的关系求得∠BPE＝90°，证明 A、P、F、 D 四点共圆，得∠AFD＝∠APD，可得结论． 【解答】解：连接 AF， ∵E，F 分别是正方形 ABCD 边 BC，CD 的中点， ∴CF＝BE， ， 在△ABE 和△BCF 中， ， ∴Rt△ABE≌Rt△BCF（SAS）， ∴∠BAE＝∠CBF， 又∵∠BAE+∠BEA＝90°， ∴∠CBF+∠BEA＝90°， ∴∠BPE＝∠APF＝90°， ∵∠ADF＝90°， ∴∠ADF+∠APF＝180°， ∴A、P、F、D 四点共圆， ∴∠AFD＝∠APD， ∴tan∠APD＝tan∠AFD＝ ＝2， 故答案为：2． 【点评】本题主要考查了正方形的性质、全等三角形的判定和性质、四点共圆的性质、 三角函数的定义，解决的关键是证明∠APF＝90°． 三、解答题（本大题共 9 个小题，满分 58 分．请考生用黑色碳素笔在答题卡相应的题号后 的答题区域内作答，必须写出运算步骤、推理过程或文字说明，超出答题区域的作答无效） 15．（5 分）计算：（3.14﹣ π ）0+| ﹣1|﹣2cos45°+（﹣1）2019． 【考点】2C：实数的运算；6E：零指数幂；T5：特殊角的三角函数值． 菁优网版 权所有 【分析】分别计算出（3.14﹣ π ）0＝1，| ﹣1|＝ ﹣1，2cos45°＝2× ＝ ，+（﹣ 1）2019＝1 即可求解； 【解答】解：（3.14﹣ π ）0+| ﹣1|﹣2cos45°+（﹣1）2019 ＝1+ ﹣1﹣2× ﹣1 ＝﹣1； 【点评】本题考查实数的运算；熟练掌握零指数幂的运算，特殊三角函数值是解题的关 键． 16．（5 分）先化简，再求值：（ ﹣1）÷ ，然后从 0，1，2 三个数中选择一 个恰当的数代入求值． 【考点】6D：分式的化简求值． 菁优网版 权所有 【分析】先根据分式的混合运算顺序和运算法则化简原式，再选取使分式有意义的 x 的 值代入计算可得． 【解答】解：原式＝（ ﹣ ）÷ ＝ • ＝ ， 当 x＝0 时，原式＝﹣1． 【点评】本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和 运算法则． 17．（5 分）如图，在平行四边形 ABCD 中，连接对角线 AC，延长 AB 至点 E，使 BE＝AB， 连接 DE，分别交 BC，AC 交于点 F，G． （1）求证：BF＝CF； （2）若 BC＝6，DG＝4，求 FG 的长． 【考点】KD：全等三角形的判定与性质；L5：平行四边形的性质；S9：相似三角形的判 定与性质．菁优网版 权所有 【分析】（1）根据平行四边形的性质得到 AD∥CD，AD＝BC，得到△EBF∽△EAD，根 据相似三角形的性质证明即可； （2）根据相似三角形的性质列式计算即可． 【解答】（1）证明：∵四边形 ABCD 是平行四边形， ∴AD∥CD，AD＝BC， ∴△EBF∽△EAD， ∴ ＝ ＝ ， ∴BF＝ AD＝ BC， ∴BF＝CF； （2）解：∵四边形 ABCD 是平行四边形， ∴AD∥CD， ∴△FGC∽△DGA， ∴ ＝ ，即 ＝ ， 解得，FG＝2． 【点评】本题考查的是相似三角形的判定和性质、平行四边形的性质，掌握相似三角形 的判定定理和性质定理是解题的关键． 18．（6 分）某社区购买甲、乙两种树苗进行绿化，已知甲种树苗每棵 30 元，乙种树苗每棵 20 元，且乙种树苗棵数比甲种树苗棵数的 2 倍少 40 棵，购买两种树苗的总金额为 9000 元． （1）求购买甲、乙两种树苗各多少棵？ （2）为保证绿化效果，社区决定再购买甲、乙两种树苗共 10 棵，总费用不超过 230 元， 求可能的购买方案？ 【考点】9A：二元一次方程组的应用；C9：一元一次不等式的应用． 菁优网版 权所有 【分析】（1）设购买甲种树苗 x 棵，购买乙种树苗（2x﹣40）棵，由题意可得，30x+20 （2x﹣40）＝9000； （2）设购买甲树苗 y 棵，乙树苗（10﹣y）棵，根据题意可得，30y+20（10﹣y）≤230， 根据 y 的范围确定购买方案即可； 【解答】解：（1）设购买甲种树苗 x 棵，购买乙种树苗（2x﹣40）棵， 由题意可得，30x+20（2x﹣40）＝9000， 70x＝9800， x＝140， ∴购买甲种树苗 140 棵，乙种树苗 240 棵； （2）设购买甲树苗 y 棵，乙树苗（10﹣y）棵， 根据题意可得，30y+20（10﹣y）≤230， 10y≤30， ∴y≤3； 购买方案 1：购买甲树苗 3 棵，乙树苗 7 棵； 购买方案 2：购买甲树苗 2 棵，乙树苗 8 棵； 购买方案 3：购买甲树苗 1 棵，乙树苗 9 棵； 购买方案 4：购买甲树苗 0 棵，乙树苗 10 棵； 【点评】本题考查一元一次方程的应用，一元一次不等式的应用；能够准确列出方程， 根据题意确定不等式是解题的关键． 19．（6 分）阅读下面的材料： 按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项．排在第 一位的数称为第一项，记为 a1，排在第二位的数称为第二项，记为 a2，依此类推，排在 第 n 位的数称为第 n 项，记为 an．所以，数列的一般形式可以写成：a1，a2，a3，…，an，…． 一般地，如果一个数列从第二项起，每一项与它前一项的差等于同一个常数，那么这个 数列叫做等差数列，这个常数叫做等差数列的公差，公差通常用 d 表示．如：数列 1，3， 5，7，…为等差数列，其中 a1＝1，a2＝3，公差为 d＝2． 根据以上材料，解答下列问题： （1）等差数列 5，10，15，…的公差 d 为 5 ，第 5 项是 25 ． （2）如果一个数列 a1，a2，a3，…，an…，是等差数列，且公差为 d，那么根据定义可 得到：a2﹣a1＝d，a3﹣a2＝d，a4﹣a3＝d，…，an﹣an﹣1＝d，…． 所以 a2＝a1+d a3＝a2+d＝（a1+d）+d＝a1+2d， a4＝a3+d＝（a1+2d）+d＝a1+3d， …… 由此，请你填空完成等差数列的通项公式：an＝a1+（ n﹣1 ）d． （3）﹣4041 是不是等差数列﹣5，﹣7，﹣9…的项？如果是，是第几项？ 【考点】37：规律型：数字的变化类． 菁优网版 权所有 【分析】（1）根据公差定义进行计算得 d，再推算第 5 项便可； （2）由 a2＝a1+d，a3＝a1+2d，a4＝a1+3d…可知：序列号 n 比 d 的系数小 1，故：an＝ a1+（n﹣1）d． （3）先根据样例求出通项公式，再将﹣4041 代入通项公式求出 n，若 n 为正整数就可以 断定﹣4041 是此等差数列的某一项，反之则不是． 【解答】解：（1）根据题意得，d＝10﹣5＝5； ∵a3＝15， a4＝a3+d＝15+5＝20， a5＝a4+d＝20+5＝25， 故答案为：5；25． （2）∵a2＝a1+d a3＝a2+d＝（a1+d）+d＝a1+2d， a4＝a3+d＝（a1+2d）+d＝a1+3d， …… ∴an＝a1+（n﹣1）d 故答案为：n﹣1． （3）根据题意得， 等差数列﹣5，﹣7，﹣9…的项的通项公式为：an＝﹣5﹣2（n﹣1）， 则﹣5﹣2（n﹣1）＝﹣4 041， 解之得：n＝2019 ∴﹣4041 是等差数列﹣5，﹣7，﹣9…的项，它是此数列的第 2019 项． 【点评】本题考查了学生的分析、阅读等自学能力，解题的关键是要认真阅读题目，理 解题目呈现的数学思想及数学方法． 20．（6 分）天门山索道是世界最长的高山客运索道，位于张家界天门山景区．在一次检修 维护中，检修人员从索道 A 处开始，沿 A﹣B﹣C 路线对索道进行检修维护．如图：已知 AB＝500 米，BC＝800 米，AB 与水平线 AA1 的夹角是 30°，BC 与水平线 BB1 的夹角是 60°．求：本次检修中，检修人员上升的垂直高度 CA1 是多少米？（结果精确到 1 米， 参考数据： ≈1.732） 【考点】T8：解直角三角形的应用．菁优网版 权所有 【分析】测不易直接测量的物体的高度、测河宽等，关键在于构造出直角三角形，通过 测量角的度数和测量边的长度，计算出所要求的物体的高度或长度．根据题目已知特点 选用适当锐角三角函数或边角关系去解直角三角形，得到数学问题的答案，再转化得到 实际问题的答案． 【解答】解：如图，过点 B 作 BH⊥AA1 于点 H． 在 Rt△ABH 中，AB＝500，∠BAH＝30°， ∴BH＝ AB＝ （米）， ∴A1B1＝BH＝250（米）， 在 Rt△BB1C 中，BC＝800，∠CBB1＝60°， ∴ ， ∴B1C＝ ＝400 （米）， ∴检修人员上升的垂直高度 CA1＝CB1+A1B1＝400 +250≈943（米） 答：检修人员上升的垂直高度 CA1 为 943 米． 【点评】本题考查了解直角三角形，熟练应用锐角三角函数关系是解题关键． 21．（7 分）如图，AB 为 ⊙ O 的直径，且 AB＝4 ，点 C 是 上的一动点（不与 A，B 重 合），过点 B 作 ⊙ O 的切线交 AC 的延长线于点 D，点 E 是 BD 的中点，连接 EC． （1）求证：EC 是 ⊙ O 的切线； （2）当∠D＝30°时，求阴影部分面积． 【考点】ME：切线的判定与性质；MO：扇形面积的计算．菁优网版 权所有 【分析】（1）连接 BC，OC，OE，由 E 是 BD 的中点，可得 CE＝BE，证明△OCE≌△ OBE，得∠OCE＝∠OBE＝90°，则结论得证； （2）阴影部分的面积即为四边形 OBED 的面积减去扇形 COB 的面积． 【解答】解：（1）如图，连接 BC，OC，OE， ∵AB 为 ⊙ O 的直径， ∴∠ACB＝90°， 在 Rt△BDC 中，∵BE＝ED， ∴DE＝EC＝BE， ∵OC＝OB，OE＝OE， ∴△OCE≌△OBE（SSS）， ∴∠OCE＝∠OBE， ∵BD 是 ⊙ O 的切线， ∴∠ABD＝90°， ∴∠OCE＝∠ABD＝90°， ∵OC 为半径， ∴EC 是 ⊙ O 的切线； （2）∵OA＝OB，BE＝DE， ∴AD∥OE， ∴∠D＝∠OEB， ∵∠D＝30°， ∴∠OEB＝30°，∠EOB＝60°， ∴∠BOC＝120°， ∵AB＝4 ， ∴OB＝2 ， ∴ ． ∴四边形 OBEC 的面积为 2S△OBE＝2× ＝12 ， ∴阴影部分面积为 S 四边形 OBEC﹣S 扇形 BOC＝12 ﹣ ＝12 ﹣4 π ． 【点评】此题综合考查了直角三角形的性质、等腰三角形的性质、切线的判定方法、扇 形的面积计算方法． 22．（8 分）为了响应市政府号召，某校开展了“六城同创与我同行”活动周，活动周设置 了“A：文明礼仪，B：生态环境 ，C：交通安全，D：卫生保洁”四个主题，每个学生 选一个主题参与．为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调 查结果绘制了如下条形统计图和扇形统计图． （1）本次随机调查的学生人数是 60 人； （2）请你补全条形统计图； （3）在扇形统计图中，“B”所在扇形的圆心角等于 108 度； （4）小明和小华各自随机参加其中的一个主题活动，请用画树状图或列表的方式求他们 恰好选中同一个主题活动的概率． 【考点】VB：扇形统计图；VC：条形统计图；X6：列表法与树状图法． 菁优网版 权所有 【分析】（1）用“A”的频数除以所占比例即可得出答案； （2）求出“C”的频数，补全条形统计图即可； （3）用 360°乘以“B”所占的比例即可； （4）画出树状图，由概率公式即可得出结果． 【解答】解：（1）本次随机调查的学生人数＝15÷25%＝60 人； 故答案为：60； （2）60﹣15﹣18﹣9＝18（人），补全条形统计图如图 1 所示： （3）在扇形统计图中，“B”所在扇形的圆心角＝360°× ＝108°， 故答案为：108； （4）画树状图如图 2 所示： 共有 16 个等可能的结果， 小明和小华恰好选中同一个主题活动的结果有 4 个， ∴小明和小华恰好选中同一个主题活动的概率＝ ＝ ． 【点评】本题考查了列表法与树状图法、扇形统计图、条形统计图；读懂题意，画出树 状图是解题的关键． 23．（10 分）已知抛物线 y＝ax2+bx+c（a≠0）过点 A（1，0），B（3，0）两点，与 y 轴交 于点 C，OC＝3． （1）求抛物线的解析式及顶点 D 的坐标； （2）过点 A 作 AM⊥BC，垂足为 M，求证：四边形 ADBM 为正方形； （3）点 P 为抛物线在直线 BC 下方图形上的一动点，当△PBC 面积最大时，求点 P 的坐 标； （4）若点 Q 为线段 OC 上的一动点，问：AQ+ QC 是否存在最小值？若存在，求岀这 个最小值；若不存在，请说明理由． 【考点】HF：二次函数综合题． 菁优网版 权所有 【分析】（1）函 数的表达式为：y＝a（x﹣1）（x﹣3）＝a（x2﹣4x+3），即可求解； （2）AM＝MB＝ABsin45°＝ ＝AD＝BD，则四边形 ADBM 为菱形，而∠AMB＝90°， 即可求解； （3）S△PBC＝ PH×OB，即可求解； （4）过点 C 作与 y 轴夹角为 30°的直线 CH，过点 A 作 AH⊥CH，垂足为 H，则 HQ＝ CQ， AQ+ QC 最小值＝AQ+HQ＝AH，即可求解． 【解答】解：（1）函数的表达式为：y＝a（x﹣1）（x﹣3）＝a（x2﹣4x+3）， 即：3a＝3，解得：a＝1， 故抛物线的表达式为：y＝x2﹣4x+3， 则顶点 D（2，﹣1）； （2）∵OB＝OC＝4，∴∠OBC＝∠OCB＝45°， AM＝MB＝ABsin45°＝ ＝AD＝BD， 则四边形 ADBM 为菱形，而∠AMB＝90°， ∴四边形 ADBM 为正方形； （3）将点 B、C 的坐标代入一次函数表达式：y＝mx+n 并解得： 直线 BC 的表达式为：y＝﹣x+3， 过点 P 作 y 轴的平行线交 BC 于点 H， 设点 P（x，x2﹣4x+3），则点 H（x，﹣x+3）， 则 S△PBC＝ PH×OB＝ （﹣x+3﹣x2+4x﹣3）＝ （﹣x2+3x）， ∵﹣ ＜0，故 S△PBC 有最大值，此时 x＝ ， 故点 P（ ，﹣ ）； （4）存在，理由： 如上图，过点 C 作与 y 轴夹角为 30°的直线 CH，过点 A 作 AH⊥CH，垂足为 H， 则 HQ＝ CQ， AQ+ QC 最小值＝AQ+HQ＝AH， 直线 HC 所在表达式中的 k 值为 ，直线 HC 的表达式为：y＝ x+3… ①则直线 AH 所在表达式中的 k 值为﹣ ， 则直线 AH 的表达式为：y＝﹣ x+s，将点 A 的坐标代入上式并解得： 则直线 AH 的表达式为：y＝﹣ x+ … ② ， 联立 ①② 并解得：x＝ ， 故点 H（ ， ），而点 A（1，0）， 则 AH＝ ， 即：AQ+ QC 的最小值为 ． 【点评】本题是二次函数综合运用，涉及到一次函数、特殊四边形性质、图形的面积计 算等，其中（4），过点 C 作与 y 轴夹角为 30°的直线 CH，则 HQ＝ CQ，是本题的难 点． 声明：试 题解析著作权 属菁优网所有 ，未经书面同 意，不得复制 发布 日期：2019/8/5 11:13:15 ；用户： 学无止境；邮 箱：419793282@qq.com ；学号： 7910509