2018年贵州省安顺市中考数学试卷含答案 12页

‎2018年安顺市初中毕业生学业、升学（高中、中职、五年制专科）‎ 招生考试 数学科试题 一、选择题（共10个小题，每小题3分，共30分）‎ ‎1.下面四个手机应用图标中是轴对称图形的是（ ）‎ A． B． C． D．‎ ‎2.的算术平方根为（ ）‎ A． B． C． D．‎ ‎3.“五·一”期间，美丽的黄果树瀑布景区吸引大量游客前来游览.经统计，某段时间内来该风景区游览的人数约为人，用科学记数法表示为（ ）‎ A． B． C． D．‎ ‎4.如图，直线，直线与直线，分别相交于、两点，过点作直线的垂线交直线于点，若，则的度数为（ ）‎ A． B． C． D．‎ ‎5.如图，点，分别在线段，上，与相交于点，已知，现添加以下哪个条件仍不能判定（ ）‎ 12‎ A． B． C． D．‎ ‎6.一个等腰三角形的两条边长分别是方程的两根，则该等腰三角形的周长是（ ）‎ A． B． C． D．或 ‎7.要调查安顺市中学生了解禁毒知识的情况，下列抽样调查最适合的是（ ）‎ A．在某中学抽取名女生 B．在安顺市中学生中抽取名学生 C．在某中学抽取名学生 D．在安顺市中学生中抽取名男生 ‎8.已知，用尺规作图的方法在上确定一点，使，则符合要求的作图痕迹是（ ）‎ A． B． ‎ ‎ C． D．‎ ‎9.已知的直径，是的弦，，垂足为，且，则的长为（ ）‎ A． B． C．或 D．或 12‎ ‎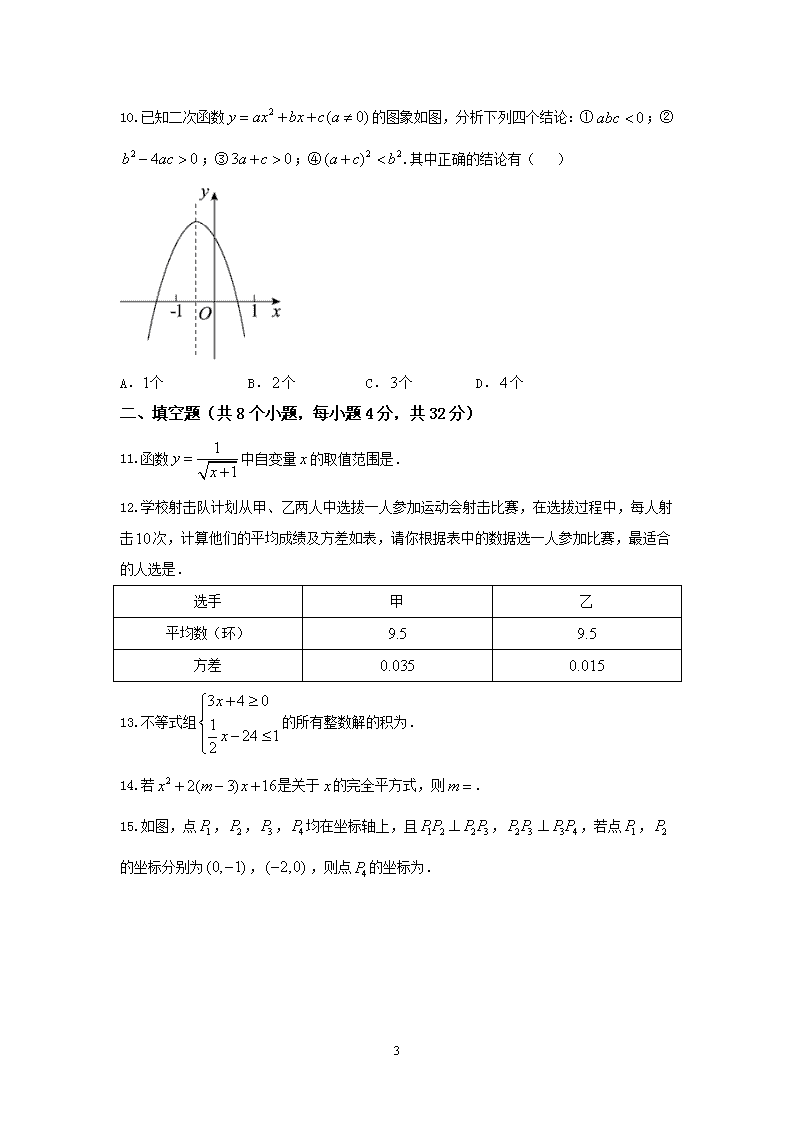10.已知二次函数的图象如图，分析下列四个结论：①；②；③；④.其中正确的结论有（ ）‎ A．个 B．个 C．个 D．个 二、填空题（共8个小题，每小题4分，共32分）‎ ‎11.函数中自变量的取值范围是．‎ ‎12.学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛，在选拔过程中，每人射击次，计算他们的平均成绩及方差如表，请你根据表中的数据选一人参加比赛，最适合的人选是．‎ 选手 甲 乙 平均数（环）‎ 方差 ‎13.不等式组的所有整数解的积为．‎ ‎14.若是关于的完全平方式，则．‎ ‎15.如图，点，，，均在坐标轴上，且，，若点，的坐标分别为，，则点的坐标为．‎ 12‎ ‎16.如图，为半圆内一点，为圆心，直径长为，，，将绕圆心逆时针旋转至，点在上，则边扫过区域（图中阴影部分）的面积为．（结果保留）‎ ‎17.如图，已知直线与轴、轴相交于、两点，与的图象相交于、两点，连接、.给出下列结论：‎ ‎①；②；③；④不等式的解集是或.‎ 其中正确结论的序号是．‎ ‎18.正方形、、、…按如图所示的方式放置.点、、、…和点、、、…分别在直线和轴上，则点的坐标是．（为正整数）‎ 12‎ 三、解答题（本大题共8小题，满分88分.解答应写出文字说明、证明过程或演算步骤）‎ ‎19.计算：.‎ ‎20.先化简，再求值：，其中.‎ ‎21.如图是某市一座人行天桥的示意图，天桥离地面的高是米，坡面的倾斜角，在距点米处有一建筑物.为了方便行人推车过天桥，市政府部门决定降低坡度，使新坡面的倾斜角，若新坡面下处与建筑物之间需留下至少米宽的人行道，问该建筑物是否需要拆除（计算最后结果保留一位小数）.‎ ‎（参考数据：，）‎ ‎22.如图，在中，是边上的中线，是的中点，过点作的平行线交的延长线于点，连接.‎ ‎（1）求证：；‎ ‎（2）若，试判断四边形的形状，并证明你的结论.‎ 12‎ ‎23.某地年为做好“精准扶贫”，投入资金万元用于异地安置，并规划投入资金逐年增加，年在年的基础上增加投入资金万元.‎ ‎（1）从年到年，该地投入异地安置资金的年平均增长率为多少？‎ ‎（2）在年异地安置的具体实施中，该地计划投入资金不低于万元用于优先搬迁租房奖励，规定前户（含第户）每户每天奖励元，户以后每户每天奖励元，按租房天计算，求年该地至少有多少户享受到优先搬迁租房奖励.‎ ‎24.某电视台为了解本地区电视节目的收视情况，对部分市民开展了“你最喜爱的电视节目”的问卷调查（每人只填写一项），根据收集的数据绘制了两幅不完整的统计图（如图所示），根据要求回答下列问题：‎ ‎（1）本次问卷调查共调查了________名观众；图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________；‎ ‎（2）补全图①中的条形统计图；‎ ‎（3）现有最喜爱“新闻节目”（记为），“体育节目”（记为），“综艺节目”（记为），“科普节目”（记为）的观众各一名，电视台要从四人中随机抽取两人参加联谊活动，请用列表或画树状图的方法，求出恰好抽到最喜爱“”和“”两位观众的概率.‎ ‎25.如图，在中，，为的中点，与半圆相切于点.‎ ‎（1）求证：是半圆所在圆的切线；‎ ‎（2）若，，求半圆所在圆的半径.‎ 12‎ ‎26.如图，已知抛物线的对称轴为直线，且抛物线与轴交于、两点，与轴交于点，其中，.‎ ‎（1）若直线经过、两点，求直线和抛物线的解析式；‎ ‎（2）在抛物线的对称轴上找一点，使点到点的距离与到点的距离之和最小，求出点的坐标；‎ ‎（3）设点为抛物线的对称轴上的一个动点，求使为直角三角形的点的坐标.‎ 12‎ ‎2018年安顺市初中毕业生学业、升学（高中、中职、五年制专科）招生考试 数学学科参考答案 一、选择题 ‎1-5: DBACD 6-10: ABDCB 二、填空题 ‎11. 12. 乙 13. 0 14. 7或-1 15. ‎ ‎16. 17. ②③④ 18.‎ 三、解答题 ‎19.解：原式.‎ ‎20.解：原式 ‎.‎ ‎∵，∴，舍，‎ 当时，原式.‎ ‎21.解：由题意得，米，米，‎ 在中，，‎ ‎∴，‎ 在中，，‎ ‎∴，‎ ‎∴（米），‎ ‎∵米米，‎ ‎∴该建筑物需要拆除.‎ 12‎ ‎22.证明：（1）∵是的中点，∴.‎ ‎∵，∴，，‎ ‎∴.‎ ‎∴.‎ ‎∵是边上的中点，∴，‎ ‎∴.‎ ‎（2）四边形是菱形.‎ 理由：由（1）知，，‎ ‎∵，∴四边形是平行四边形.‎ 又∵，∴是直角三角形.‎ ‎∵是边上的中线，‎ ‎∴.‎ ‎∴平行四边形是菱形.‎ ‎23.解：（1）设该地投入异地安置资金的年平均增长率为，根据题意得 ‎，‎ 解得：或（舍），‎ 答：从年到年，该地投入异地安置资金的年平均增长率为；‎ ‎（2）设年该地有户享受到优先搬迁租房奖励，根据题意得，‎ ‎∵，∴，‎ ‎，‎ 解得：，‎ 答：年该地至少有户享受到优先搬迁租房奖励.‎ ‎24.解：（1），.‎ ‎（2）最喜爱“新闻节目”的人数为（人），如图，‎ 12‎ ‎（3）画树状图为：‎ 共有种等可能的结果，恰好抽到最喜爱“”和“”两位观众的结果数为，‎ 所以恰好抽到最喜爱“”和“”两位观众的概率.‎ ‎25.（1）证明：如图1，‎ 作于，连接、，‎ ‎∵，为的中点，‎ ‎∴.‎ ‎∵与半圆相切于点，‎ ‎∴，‎ ‎∵，‎ ‎∴，‎ ‎∵经过圆半径的外端，∴是半圆所在圆的切线；‎ ‎（2）∵，是的中点，∴，‎ 12‎ 由，，得∴.‎ 由勾股定理，得.‎ 由三角形的面积，得，‎ ‎，半圆所在圆的半径是.‎ ‎26.解：（1）依题意得：，解之得：，‎ ‎∴抛物线的解析式为.‎ ‎∵对称轴为，且抛物线经过，‎ ‎∴把、分别代入直线，‎ 得，解之得：，‎ ‎∴直线的解析式为.‎ ‎（2）直线与对称轴的交点为，则此时的值最小，把代入直线得，‎ ‎∴.即当点到点的距离与到点的距离之和最小时的坐标为.‎ ‎（注：本题只求坐标没说要证明为何此时的值最小，所以答案没证明的值最小的原因）.‎ 12‎ ‎（3）设，又，，‎ ‎∴，，，‎ ‎①若点为直角顶点，则即：解之得：，‎ ‎②若点为直角顶点，则即：解之得：，‎ ‎③若点为直角顶点，则即：解之得：‎ ‎，.‎ 综上所述的坐标为或或或.‎ 12‎