2019-2020学年北京市海淀区九年级（上）期末数学试卷 7页

‎2019-2020学年北京市海淀区九年级（上）期末数学试卷 一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个．‎ ‎ ‎ ‎1. 下列图形中既是轴对称图形，又是中心对称图形的是（ ） ‎ A. B. C. D.‎ ‎ ‎ ‎2. 五张完全相同的卡片上，分别写有数字‎1‎，‎2‎，‎3‎，‎4‎，‎5‎，现从中随机抽取一张，抽到的卡片上所写数字小于‎3‎的概率是（ ） ‎ A.‎2‎‎5‎ B.‎1‎‎5‎ C.‎4‎‎5‎ D.‎‎3‎‎5‎ ‎ ‎ ‎3. 方程x‎2‎‎−3x−1‎＝‎0‎的根的情况是（ ） ‎ A.有两个相等的实数根 B.有两个不相等的实数根 C.没有实数根 D.无法确定 ‎ ‎ ‎ ‎4. 如图，在四边形ABCD中，AD // BC，点E，F分别是边AD，BC上的点，AF与BE交于点O，AE＝‎2‎，BF＝‎1‎，则‎△AOE与‎△BOF的面积之比为（ ） ‎ A.‎1‎‎4‎ B.‎1‎‎2‎ C.‎4‎ D.‎‎2‎ ‎ ‎ ‎5. 若扇形的半径为‎2‎，圆心角为‎90‎‎∘‎，则这个扇形的面积为（ ） ‎ A.π B.π‎2‎ C.‎4π D.‎‎2π ‎ ‎ ‎6. 如图，OA交‎⊙O于点B，AD切‎⊙O于点D，点C在‎⊙O上．若‎∠A＝‎40‎‎∘‎，则‎∠C为（ ） ‎ A.‎25‎‎∘‎ B.‎20‎‎∘‎ C.‎35‎‎∘‎ D.‎‎30‎‎∘‎ ‎ ‎ ‎7. 在同一平面直角坐标系xOy中，函数y＝kx+1‎与y=kx(k≠0)‎的图象可能是（ ） ‎ A. B. C. D. ‎ ‎ ‎ ‎8. 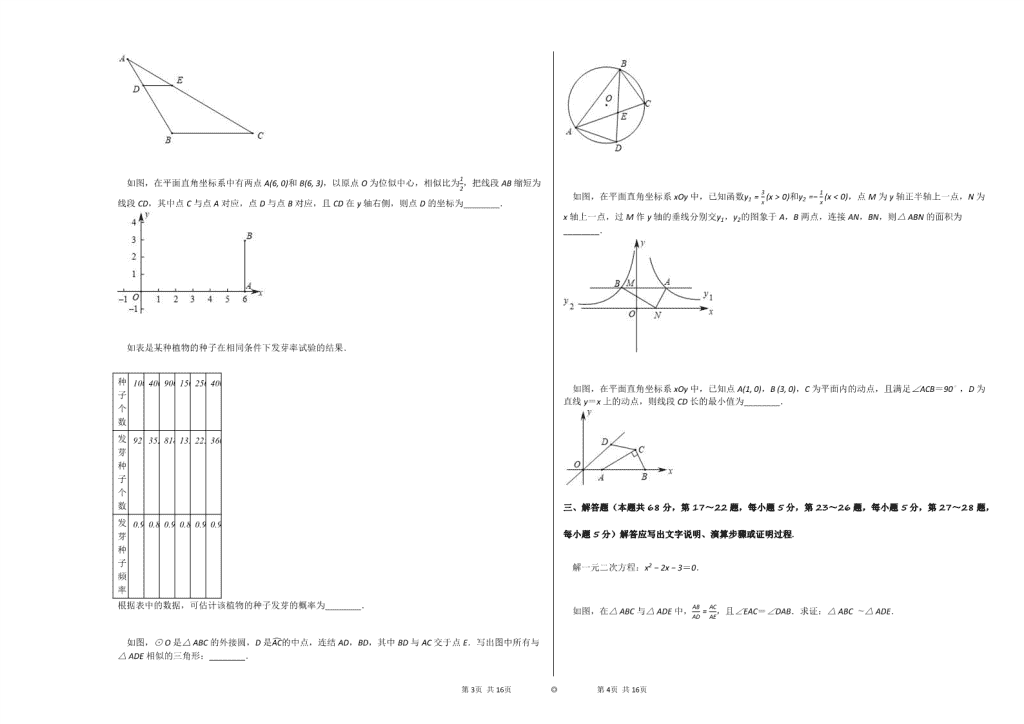在平面直角坐标系xOy中，将横纵坐标之积为‎1‎的点称为“好点”，则函数y＝‎|x|−3‎的图象上的“好点”共有（ ） ‎ A.‎2‎个 B.‎1‎个 C.‎4‎个 D.‎3‎个 二、填空题（本题共16分，每小题2分）‎ ‎ ‎ ‎ 反比例函数y=‎‎2‎x的图象经过‎(2, y‎1‎)‎，‎(3, y‎2‎)‎两点，则y‎1‎ ‎>‎ y‎2‎．（填“‎>‎”，“＝”或“‎<‎”） ‎ ‎ ‎ ‎ 如果关于x的一元二次方程ax‎2‎+bx−1‎＝‎0‎的一个解是x＝‎1‎，则‎2020−a−b＝________． ‎ ‎ ‎ 第13页 共14页 ◎ 第14页 共14页 ‎ 如图，在‎△ABC中，点D，E分别是边AB，AC上的点，DE // BC，AD＝‎1‎，BD＝AE＝‎2‎，则EC的长为________． ‎ ‎ ‎ ‎ 如图，在平面直角坐标系中有两点A(6, 0)‎和B(6, 3)‎，以原点O为位似中心，相似比为‎1‎‎2‎，把线段AB缩短为线段CD，其中点C与点A对应，点D与点B对应，且CD在y轴右侧，则点D的坐标为________． ‎ ‎ ‎ ‎ 如表是某种植物的种子在相同条件下发芽率试验的结果． ‎ 种子个数 ‎100‎ ‎400‎ ‎900‎ ‎1500‎ ‎2500‎ ‎4000‎ 发芽种子个数 ‎92‎ ‎352‎ ‎818‎ ‎1336‎ ‎2251‎ ‎3601‎ 发芽种子频率 ‎0.92‎ ‎0.88‎ ‎0.91‎ ‎0.89‎ ‎0.90‎ ‎0.90‎ 根据表中的数据，可估计该植物的种子发芽的概率为________．‎ ‎ ‎ ‎ 如图，‎⊙O是‎△ABC的外接圆，D是AC的中点，连结AD，BD，其中BD与AC交于点E．写出图中所有与‎△ADE相似的三角形：________． ‎ ‎ ‎ ‎ 如图，在平面直角坐标系xOy中，已知函数y‎1‎‎=‎3‎x(x>0)‎和y‎2‎‎=−‎1‎x(x<0)‎，点M为y轴正半轴上一点，N为x轴上一点，过M作y轴的垂线分别交y‎1‎，y‎2‎的图象于A，B两点，连接AN，BN，则‎△ABN的面积为________． ‎ ‎ ‎ ‎ 如图，在平面直角坐标系xOy中，已知点A(1, 0)‎，B (3, 0)‎，C为平面内的动点，且满足‎∠ACB＝‎90‎‎∘‎，D为直线y＝x上的动点，则线段CD长的最小值为________． ‎ 三、解答题（本题共68分，第17～22题，每小题5分，第23～26题，每小题5分，第27～28题，每小题5分）解答应写出文字说明、演算步骤或证明过程.‎ ‎ ‎ ‎ 解一元二次方程：x‎2‎‎−2x−3‎＝‎0‎． ‎ ‎ ‎ ‎ 如图，在‎△ABC与‎△ADE中，ABAD‎=‎ACAE，且‎∠EAC＝‎∠DAB．求证：‎△ABC∼△ADE． ‎ ‎ ‎ ‎ 某司机驾驶汽车从甲地去乙地，他以‎80km/h的平均速度用‎6h到达目的地． ‎ ‎（1）当他按原路匀速返回时，汽车的速度v与时间t有怎样的函数关系？‎ ‎ ‎ ‎（2）如果该司机返回到甲地的时间不超过‎5h，那么返程时的平均速度不能小于多少？‎ ‎ ‎ 第13页 共14页 ◎ 第14页 共14页 ‎ 如图，在‎⊙O中，AC‎=‎CB，CD⊥OA于点D，CE⊥OB于点E． ‎ ‎（1）求证：CD＝CE；‎ ‎ ‎ ‎（2）若‎∠AOB＝‎120‎‎∘‎，OA＝‎2‎，求四边形DOEC的面积．‎ ‎ ‎ ‎ 已知关于x的一元二次方程x‎2‎‎−mx+m−1‎＝‎0‎． ‎ ‎（1）求证：方程总有两个实数根；‎ ‎ ‎ ‎（2）若方程有一个根为负数，求m的取值范围．‎ ‎ ‎ ‎ 一个不透明的布袋中有完全相同的三个小球，把它们分别标号为‎1‎，‎2‎，‎3‎．小林和小华做一个游戏，按照以下方式抽取小球：先从布袋中随机抽取一个小球，记下标号后放回布袋中搅匀，再从布袋中随机抽取一个小球，记下标号．若两次抽取的小球标号之和为奇数，小林赢；若标号之和为偶数，则小华赢． ‎ ‎（1）用画树状图或列表的方法，列出前后两次取出小球上所标数字的所有可能情况；‎ ‎ ‎ ‎（2）请判断这个游戏是否公平，并说明理由．‎ ‎ ‎ ‎ 如图，‎∠ABC＝‎90‎‎∘‎，AB＝‎2‎，BC＝‎8‎，射线CD⊥BC于点C，E是线段BC上一点，F是射线CD上一点，且满足‎∠AEF＝‎90‎‎∘‎． ‎ ‎（1）若BE＝‎3‎，求CF的长；‎ ‎ ‎ ‎（2）当BE的长为何值时，CF的长最大，并求出这个最大值．‎ ‎ ‎ ‎ 在平面直角坐标系xOy中，已知点A是直线y=‎1‎‎2‎x+‎‎3‎‎2‎上一点，过点A分别作x轴，y轴的垂线，垂足分别为点B和点C，反比例函数y=‎kx的图象经过点A． ‎ ‎（1）若点A是第一象限内的点，且AB＝AC，求k的值；‎ ‎ ‎ ‎（2）当AB>AC时，直接写出k的取值范围．‎ ‎ ‎ ‎ 如图，AB是‎⊙O的直径，直线MC与‎⊙O相切于点C．过点A作MC的垂线，垂足为D，线段AD与‎⊙O相交于点E． ‎ ‎（1）求证：AC是‎∠DAB的平分线；‎ ‎ ‎ ‎（2）若AB＝‎10‎，AC＝‎4‎‎5‎，求AE的长．‎ ‎ ‎ ‎ 在平面直角坐标系xOy中，已知抛物线G:y＝ax‎2‎−2ax+4(a≠0)‎． ‎ ‎（1）当a＝‎1‎时， ①抛物线G的对称轴为x＝________； ②若在抛物线G上有两点‎(2, y‎1‎)‎，‎(m, y‎2‎)‎，且y‎2‎‎>‎y‎1‎，则m的取值范围是________；‎ ‎ ‎ ‎（2）抛物线G的对称轴与x轴交于点M，点M与点A关于y轴对称，将点M向右平移‎3‎个单位得到点B，若抛物线G与线段AB恰有一个公共点，结合图象，求a的取值范围．‎ ‎ ‎ 第13页 共14页 ◎ 第14页 共14页 ‎ 在Rt△ABC中，‎∠ACB＝‎90‎‎∘‎，AC＝‎1‎，记‎∠ABC＝α，点D为射线BC上的动点，连接AD，将射线DA绕点D顺时针旋转α角后得到射线DE，过点A作AD的垂线，与射线DE交于点P，点B关于点D的对称点为Q，连接PQ． ‎ ‎（1）当‎△ABD为等边三角形时， ①依题意补全图‎1‎； ②PQ的长为________；‎ ‎ ‎ ‎（2）如图‎2‎，当α＝‎45‎‎∘‎，且BD=‎‎4‎‎3‎时，求证：PD＝PQ；‎ ‎ ‎ ‎（3）设BC＝t，当PD＝PQ时，直接写出BD的长．（用含t的代数式表示）‎ ‎ ‎ ‎ 在平面直角坐标系xOy中，对于点P(a, b)‎和实数k(k>0)‎，给出如下定义：当ka+b>0‎时，将以点P为圆心，ka+b为半径的圆，称为点P的k倍相关圆． 例如，在如图‎1‎中，点P(1, 1)‎的‎1‎倍相关圆为以点P为圆心，‎2‎为半径的圆． ‎ ‎（1）在点P‎1‎‎(2, 1)‎，P‎2‎‎(1, −3)‎中，存在‎1‎倍相关圆的点是________，该点的‎1‎倍相关圆半径为________．‎ ‎ ‎ ‎（2）如图‎2‎，若M是x轴正半轴上的动点，点N在第一象限内，且满足‎∠MON＝‎30‎‎∘‎，判断直线ON与点M的‎1‎‎2‎倍相关圆的位置关系，并证明．‎ ‎ ‎ ‎（3）如图‎3‎，已知点A的‎(0, 3)‎，B(1, m)‎，反比例函数y=‎‎6‎x的图象经过点B，直线l与直线AB关于y轴对称． ①若点C在直线l上，则点C的‎3‎倍相关圆的半径为________． ②点D在直线AB上，点D的‎1‎‎3‎倍相关圆的半径为R，若点D在运动过程中，以点D为圆心，hR为半径的圆与反比例函数y=‎‎6‎x的图象最多有两个公共点，直接写出h的最大值．‎ 第13页 共14页 ◎ 第14页 共14页 参考答案与试题解析 ‎2019-2020学年北京市海淀区九年级（上）期末数学试卷 一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个．‎ ‎1.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 中心较称图腾 轴正算图形 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎2.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 概水常式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎3.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 根体判展式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎4.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎5.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 扇形体积硫计算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎6.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 圆明角研理 切表的木质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎7.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一次射可的图象 反比例射数的图放 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎8.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一次常数图按上点入适标特点 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 二、填空题（本题共16分，每小题2分）‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 反比射函可铜象上误的坐标特征 ‎【解析】‎ 第13页 共14页 ◎ 第14页 共14页 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一元二表方病的解 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 坐标正测形性质 作图使胞似变换 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 利用频都升计概率 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 圆心角、射、弦开关系 三角形的常换圆与外心 相似三使形的判碳 圆明角研理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 反比表函数弹数k蜡几何主义 反比例根数的性气 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 勾体定展 垂因丙最短 一次常数图按上点入适标特点 圆明角研理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 三、解答题（本题共68分，第17～22题，每小题5分，第23～26题，每小题5分，第27～28题，每小题5分）解答应写出文字说明、演算步骤或证明过程.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 解一较燥次延程抗因式分解法 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 第13页 共14页 ◎ 第14页 共14页 反比例表数透应用 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 勾体定展 圆心角、射、弦开关系 垂都着理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 根体判展式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 游水于平性 列表法三树状图州 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 二次常数换最值 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 反比于函数偏压史函数的综合 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 圆明角研理 切表的木质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次射数空象与话数流关系 二次常数图见合点的岸标特征 二水来数兴象触几何变换 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 几何使碳综合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 反比例表数病合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 第13页 共14页 ◎ 第14页 共14页