人教数学九上与圆有关的位置关系之一 5页

‎24.2.2直线和圆的位置关系（2）‎ 年级：九年级 科目：数学 课型：新授 主备：徐中国 审核：姜艳 薛柏双 田娟 备课时间：2010.9.17 上课时间：2010.9.26‎ 学习目标：‎ ‎1．理解并掌握切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．‎ ‎2．理解并掌握切线的性质定理：圆的切线垂直于过切点的半径 重点、难点 1、 重点：理解并掌握切线的判定定理和性质定理 2、 难点：运用切线的判定定理和性质定理解决一些具体的题目 导学过程：阅读教材P95 — 96 , 完成课前预习 ‎【课前预习】‎ ‎1：知识准备 直线和圆的位置关系表：‎ 直线和圆的位置关系 相交 相切 相离 公共点的个数 公共点名称 直线名称 圆心到直线的距离d与r的关系 ‎2：探究 思考1：如图，在⊙O中，经过半径OA的外端点A作 直线L⊥OA，则圆心O到直线L的距离是多少？‎ 直线L和⊙O有什么位置关系？‎ 切线的判定定理：经过 的外端并且 于这条半径的直线是圆的切线。‎ 思考2：将思考1中的问题反过来，如果直线L是⊙O的切线，切点为A，那么半径OA与直线L是不是一定垂直呢？‎ 切线的性质定理：圆的切线 于过切点的 。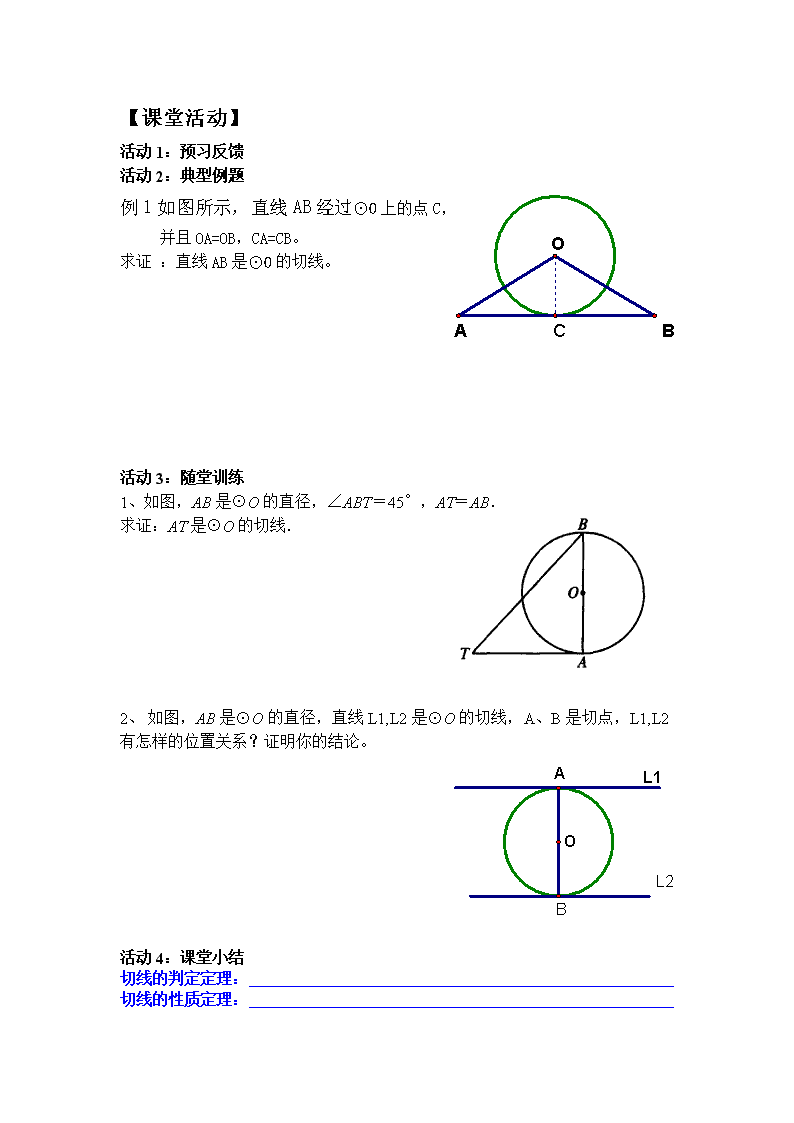‎ ‎【课堂活动】‎ 活动1：预习反馈 活动2：典型例题 例1如图所示，直线AB经过⊙O上的点C，‎ 并且OA=OB，CA=CB。‎ 求证 ：直线AB是⊙O的切线。‎ 活动3：随堂训练 ‎1、如图，AB是⊙O的直径，∠ABT＝45°，AT＝AB．‎ 求证：AT是⊙O的切线．‎ 2、 如图，AB是⊙O的直径，直线L1,L2是⊙O的切线，A、B是切点，L1,L2有怎样的位置关系？证明你的结论。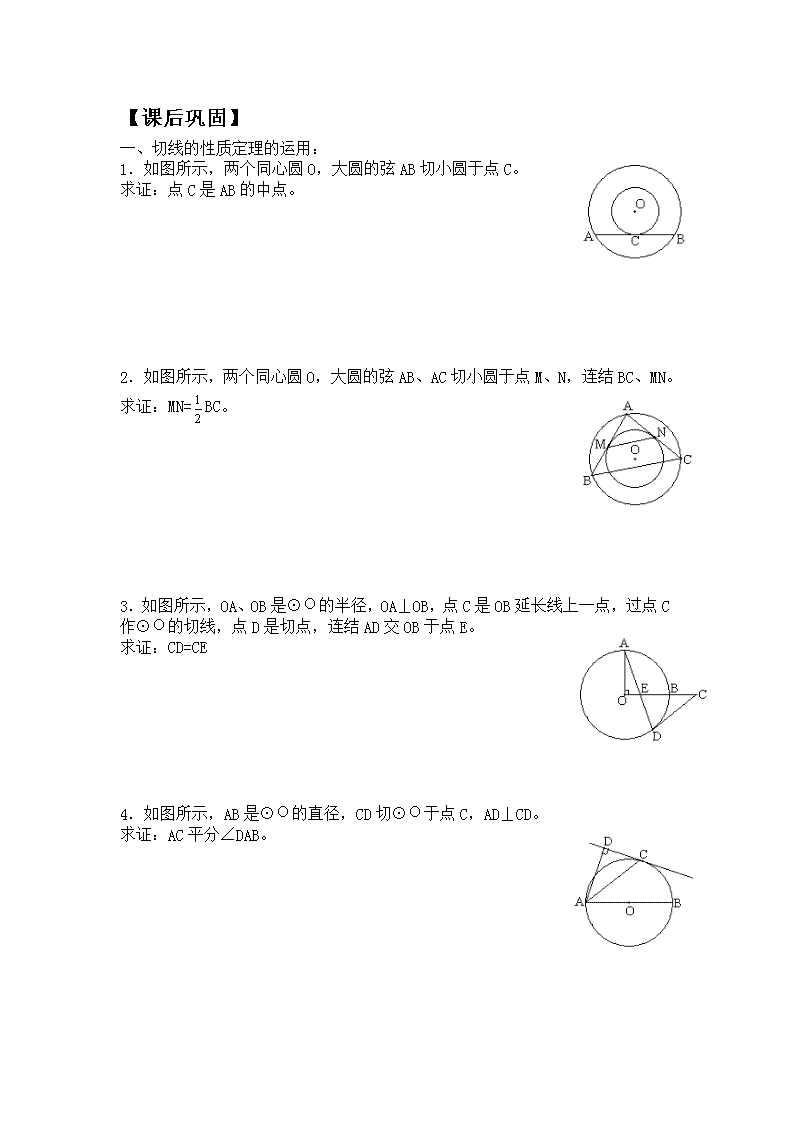‎ 活动4：课堂小结 切线的判定定理： ‎ 切线的性质定理： ‎ ‎【课后巩固】‎ 一、切线的性质定理的运用：‎ ‎1．如图所示，两个同心圆O，大圆的弦AB切小圆于点C。‎ 求证：点C是AB的中点。‎ ‎2．如图所示，两个同心圆O，大圆的弦AB、AC切小圆于点M、N，连结BC、MN。‎ 求证：MN=BC。 ‎ ‎3．如图所示，OA、OB是⊙Ｏ的半径，OA⊥OB，点C是OB延长线上一点，过点C作⊙Ｏ的切线，点D是切点，连结AD交OB于点E。‎ 求证：CD=CE ‎4．如图所示，AB是⊙Ｏ的直径，CD切⊙Ｏ于点C，AD⊥CD。‎ 求证：AC平分∠DAB。‎ 二．切线的判定定理的运用：‎ ‎1．如图所示，AB是⊙Ｏ的直径，点C在⊙Ｏ上，AC平分∠DAB ，AD⊥CD。‎ 求证：CD与⊙Ｏ相切。‎ ‎2．如图所示，OA、OB是⊙Ｏ的半径，OA⊥OB，点C是OB延长线上一点，，点D在⊙Ｏ上，连结AD交OB于点E，且CD=CE。‎ 求证：CD与⊙Ｏ相切。‎ ‎3．如图所示，点O是∠BAC的平分线AD上一点，以O为圆心的与AB相切于点M。‎ 求证：AC与⊙Ｏ相切。‎ ‎4．如图所示，AB是⊙Ｏ的直径，点D在⊙Ｏ上，BC是⊙Ｏ的切线，AD∥OC。‎ 求证：CD是⊙Ｏ的切线。‎ ‎5．如图所示，在△ABC中，AB=AC，以AB为直径的⊙Ｏ交BC于点D，DE⊥AC。‎ 求证：⑴点D是BC的中点；‎ ‎⑵DE是⊙Ｏ的切线。‎