九年级数学下册第三章圆3圆周角和圆心角的关系第1课时习题课件北师大版 30页

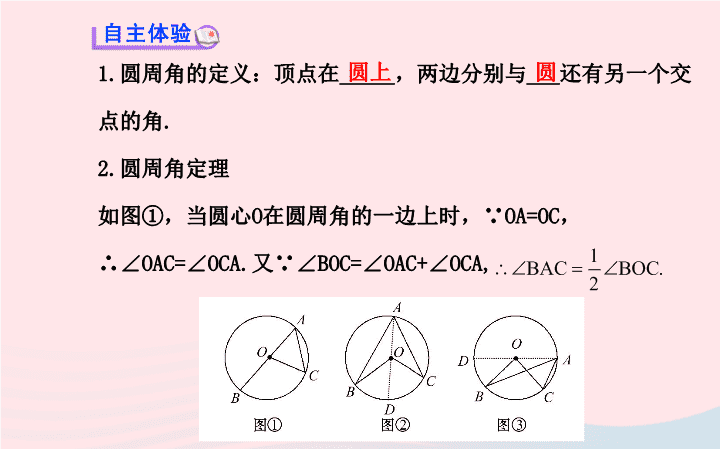
3 圆周角和圆心角的关系 第 1 课时 1. 理解圆周角的概念，掌握圆周角的两个特征、定理的内容及简单应用 .( 重点、难点 ) 2. 认识圆周角定理需分三种情况证明的必要性 .( 难点 ) 1. 圆周角的定义：顶点在 _____ ，两边分别与 ___ 还有另一个交 点的角 . 2. 圆周角定理 如图①，当圆心 O 在圆周角的一边上时，∵ OA=OC ， ∴∠ OAC=∠OCA. 又∵∠ BOC=∠OAC+∠OCA, 圆上 圆 【 思考 】 (1) 如图②，当圆心 O 在圆周角的内部时，∠ BAC 与 ∠ BOC 的上述关系是否还成立？为什么 ? 提示： 成立 . 理由如下： 作直径 AD. 由图形可知： 同理： 即 (2) 如图③，当圆心 O 在圆周角的外部时，∠ BAC 与∠ BOC 的上述 关系是否还成立？为什么 ? 提示： 成立，理由如下： 作直径 AD. 由图形可知： 同理： 即 【 总结 】 一条弧所对的圆周角等于它所对的圆心角的 _____ . 一半 ( 打“√”或“ ×”) (1) 顶点在圆心的角叫做圆心角 .( ) (2) 顶点在圆周上的角叫做圆周角 .( ) (3) 圆周角的度数是圆心角的一半 .( ) (4) 劣弧所对的圆周角都是锐角，优弧所对的圆周角都是钝角 .( ) (5) 一条弧所对的圆周角为 50° ，则它所对的圆心角为 100°.( ) √ × × √ √ 知识点 1 圆周角及圆周角定理 【 例 1】 (2013· 昭通中考 ) 如图，已知 AB ， CD 是⊙ O 的两条直径，∠ ABC=28° ，那么∠ BAD=( ) A.28° B.42° C.56° D.84° 【 思路点拨 】 找出∠ BAD 所对的弧所对的圆心角∠ BOD, 结合已知条件∠ ABC=28° ，可知∠ ABC 所对的弧所对的圆心角∠ AOC 的度数，进而确定∠ BOD ，再求出∠ BAD. 【 自主解答 】 选 A. 因为 AB ， CD 是⊙ O 的两条直径，所以 OB=OC ，所以∠ ABC= ∠ BCD=28 ° ，因为∠ BCD ，∠ BAD 都是弧 BD 所对的圆周角，所以∠ BAD= ∠ BCD=28 ° . 【 总结提升 】 圆周角与圆心角的区别与联系 　　　名称 关系　　 　　圆心角 圆周角 区别 顶点 顶点在圆心上 顶点在圆周上 个数 在同圆中 , 一条弧所对的圆心角惟一 在同圆中 , 一条弧所对的圆周角有无数个 联系 位置 两边都和圆相交 大小 关系 一条弧所对的圆周角等于它所对的圆心角的一半 知识点 2 圆周角定理的应用 【 例 2】 如图 , 在⊙ O 中 , 直径 AB 与弦 CD 相交于点 P,∠CAB ＝ 40°,∠APD ＝ 65°. (1) 求∠ ABD 的大小 . (2) 已知圆心 O 到 BD 的距离为 3, 求 AD 的长 . 【 解题探究 】 1. 连接 OC ，∠ CAB 和∠ CDB 各是什么角？有什么关 系？你能求出∠ CDB 的度数吗？ 提示： ∠ CAB 和∠ CDB 都是圆周角， 它们所对的弧所对的圆心角 都是∠ COB ，所以 2.∠APD 和∠ CDB,∠ABD 有怎样的关系？ 提示： ∠ APD 是△ BPD 的外角，有∠ APD=∠CDB+∠ABD. 3. 由 2 可求出∠ ABD =______-______=_____-_____=_____. 4. 过点 O 作 OE⊥BD 于 E, 则 OE ＝ __ ， 由垂径定理可知， BE ___ DE.∵OA ＝ OB ， ∴线段 OE 是△ ABD 的 _______ ， ∴ AD ＝ ____ ＝ __. ∠APD ∠CDB 65° 40° 25° 3 ＝ 中位线 2OE 6 【 总结提升 】 圆周角定理 一条弧所对的圆周角有无数个 , 但它们与圆心角的位置关系 , 归纳起来 , 只有三种情况： (1) 圆心在圆周角的一边上 .(2) 圆心在圆周角的内部 . (3) 圆心在圆周角的外部 . 以上三种情况 , 圆周角定理都成立 , 证明圆周角定理成立的过程 , 体现了由特殊到一般的数学思想方法 . 圆周角定理成立的前提是 “ 在同圆中 , 并且圆周角和圆心角对应同一条弧 ” , 不能简单表达为 “ 圆周角等于圆心角的一半 ” . 题组一： 圆周角及圆周角定理 1.(2013· 滨州中考 ) 如图，在⊙ O 中，圆心角∠ BOC=78° ，则 圆周角∠ BAC 的大小为 ( ) A.156° B.78° C.39° D.12° 【 解析 】 选 C. 根据在同圆或等圆中，同弧或等弧所对的圆周角 是它所对的圆心角的一半，所以 2. 如图， A ， B ， C 是⊙ O 上的三个点，∠ ABC=25° ，则∠ AOC 的度数是 ______. 【 解析 】 圆周角∠ ABC 与圆心角∠ AOC 对着同一条弧，∴∠ AOC=2∠ABC ，又∠ ABC=25° ，所以∠ AOC=50° ． 答案： 50 ° 3. 如图， A ， B ， C ， D ， E 是⊙ O 上的五个点，则图中共有 ____ 个圆周角，分别是 ________________. 【 解析 】 图中共有 6 个圆周角 , 分别是∠ ACB ，∠ ACE ，∠ BCE ，∠ BDE ，∠ CED ，∠ CBD. 答案： 6 ∠ACB ，∠ ACE ，∠ BCE ，∠ BDE ，∠ CED ，∠ CBD 4. 如图，若 AB 是⊙ O 的直径， CD 是⊙ O 的弦，∠ ABD=55° ，则∠ BCD 的度数为 __________. 【 解析 】 连接 OD, ∵∠ABD=55°, ∴∠AOD=2∠ABD=110°, 又∵∠ AOD +∠BOD =180° ， ∴∠ BOD=70° ， 答案： 35 ° 5. 将量角器按如图所示的方式放置在三角形纸板上 , 使点 C 在半 圆上 . 点 A ， B 的读数分别为 86° ， 30°, 则∠ ACB 的大小为 _____. 【 解析 】 设半圆的圆心为 O, 连接 OA,OB, 则圆心角∠ AOB=56°, 因此圆周角 答案： 28 ° 6.(2013· 黔西南州中考 ) 如图所示⊙ O 中，已知 ∠ BAC=∠CDA=20° ，则∠ ABO 的度数为 __________. 【 解析 】 连接 OA ， OC ，则∠ COB=2∠BAC=40° ， ∠ AOC=2∠CDA=40° ，所以∠ AOB=80° ， 所以∠ ABO=(180°-80°)÷2=50°. 答案： 50° 题组二： 圆周角定理的应用 1. 如图， A,B,C 在⊙ O 上，已知∠ ABO ＝ 40° ，则∠ ACB 的大小为 ( ) A.40° B.30° C.50° D.60° 【 解析 】 选 C. 在⊙ O 中， OA ＝ OB ，所以∠ ABO ＝∠ BAO ＝ 40 ° ， 所以∠ AOB ＝ 100 ° ，所以 2. 如图，在△ ABC 中， AB 为⊙ O 的直径，∠ ABC=60° ，∠ BOD=100° ，则∠ C 的度数为 ( ) A ． 50° B ． 60° C ． 70° D ． 80° 【 解析 】 选 C. 因为∠ BOD=100 ° ，所以∠ OAD=50 ° ，又因为∠ ABC=60 ° ，所以∠ C ＝ 180 ° -60 ° -50 ° ＝ 70 ° . 3. 如图 , 点 O 为优弧 所在圆的圆心 ,∠AOC=108°, 点 D 在 AB 的 延长线上 ,BD=BC, 则∠ D=________. 【 解析 】 由圆周角的性质可得 , 答案： 27° 4. 在⊙ O 中，直径 AB⊥CD 于点 E ，连接 CO 并延长交 AD 于点 F, 且 CF⊥AD. 求∠ ADC 的度数 . 【 解析 】 ∵ 在⊙ O 中， D 为圆上一点， ∴∠ AOC=2 ∠ ADC. ∴∠ EOF= ∠ AOC=2 ∠ ADC. 在四边形 FOED 中，∠ CFD+ ∠ ADC+ ∠ DEO+ ∠ FOE=360 ° , ∴ 90 ° + ∠ ADC+90 ° +2 ∠ ADC=360 ° , ∴∠ ADC=60 ° . 5. 如图，在⊙ O 中， AB 是直径， CD 是弦， AB⊥CD. (1)P 是 上一点 ( 不与 C,D 重合 ) ，试判断∠ CPD 与∠ COB 的大 小关系，并说明理由 . (2)P ′ 是 上一点 ( 不与 C,D 重合 ) ，试判断∠ CP ′ D 与∠ COB 有 什么关系？并证明你的结论 . 【 解析 】 (1)∠CPD=∠COB. 连接 OD. ∵AB 是直径， AB⊥CD ， (2)∠COB+∠CP′D=180°. ∵∠CPD+∠CP′D=180° ，∠ CPD=∠COB ， ∴∠ CP′D+∠COB=180°. 【 变式备选 】 点 A,B,C 在⊙ O 上，若∠ AOC ＝ 160° ，则∠ ABC 的度数是 ( ) A.80° B.160° C.100 ° D.80 ° 或 100 ° 【 解析 】 选 D. 如图： ①若点 O 在△ AB 1 C 内部， ②若点 O 在△ AB 2 C 外部 ( 在△ AB 1 C 内部 ) ， ∵四边形 AB 1 CB 2 内接于⊙ O ， ∴∠ AB 2 C ＋∠ AB 1 C ＝ 180° ， 此时，∠ AB 2 C ＝ 180 ° － 80 ° ＝ 100 ° . 【 想一想错在哪？ 】 在半径为 R 的圆中，有一条弦分圆周为 1∶2 两部分，则弦所对的圆周角为 ____________. 提示： 弦所对的圆周角有两个，忽略了优弧所对的圆周角 .