2014年1月普陀中考数学一模试题 8页

普陀区 2013 一模——数学卷 一、选择题 1. 用放大镜将图形放大，应该属于（ ） A. 平移变换 B. 相似变换 C. 对称变换 D. 旋转变换 2. 在比例尺是 1:38000 的黄浦江交通游览图上，某隧道长约 7cm，它的实际长度约为（ ） A. 0.266km B. 2.66km C. 26.6km D. 266km 3. 在 ABC 中， tan 1,cot 3AB，那么 是（ ） A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 等腰三角形 4. 二次函数  2 2 3 0y ax x a    的图像一定不经过（ ） A. 第一象限 B. 第二象限 C. 第二象限 D. 第二象限 5. 下列命题中，正确的是（ ） A. 如果一条直线截三角形两边的延长线所得的对应线段成比例，那么这条直线一定平行于 三角形的第三边 B. 不同向量的单位向量的长度都相等，方向也都相同 C. 相似三角形的中线的比等于相似比 D. 一般来说，一条线段的黄金分割点有两个 6. 在 Rt ABC 中， 90 , ,A AC a ACB       ，那么下面各式正确的是（ ） A. sinAB a  B. cosAB a  C. tanAB a  D. cotAB a  二、填空题： 7. 如图，直线 AD ∥ BE ∥CF , 1 ,43BC AC DE,那么 EF 的值是__________。 8. 在一陡坡上前进 5 米，水平高度升高了 3 米，则坡度i __________。 9. 抛物线 2 1yx关于 x 轴对称的抛物线的解析式为___________。 10. 请写出一个以直线 2x  为对称轴，且在对称轴左侧部分是上升的抛物线的表达式可以是_________。 11. 如果 EF、 是 ABC 的边 AB 和 AC 的中点， ,AB a AC b，那么 EF _________。 12. 如图，在边长为 1 的正方形网格上有点 P A B C、 、 、 ，则图中所形成的三角形中，相似的三角形______。 13. 已知 为一锐角，且cos sin60 ，则  __________。 14. 若 为一锐角，化简：  2sin 1 sin   ____________。 15. 如果直角三角形的斜边长为 12，那么它的重心与外心之间的距离为________。 16. 已知二次函数的顶点坐标为 2,3 ，并且经过平移后与抛物线 22yx 重合，那么这个二次函数的 F E D C B A P CB A 解析式为_________。 17. 若一个三角形的边长均满足方程 2 6 8 0xx   ，则此三角形的周长为____________。 18. 已知梯形 ABCD中，AD ∥ BC ， 15, 13, 8,AB CD AD B    是锐角， B 的正弦值为 4 5 ，那么 BC 的长为_________。 三、解答题 19. 计算：   sin 60 3tan30 cos60 1 2cot 45 cot 30        20. 已知：如图， ABC 中，点 D 是 AC 边上一点，且 : 2:1AD DC  , （1）设 ,BA a BC b，先化简，再求作： （2）用 xa yb （ xy、 为实数）的行驶表示 BD 。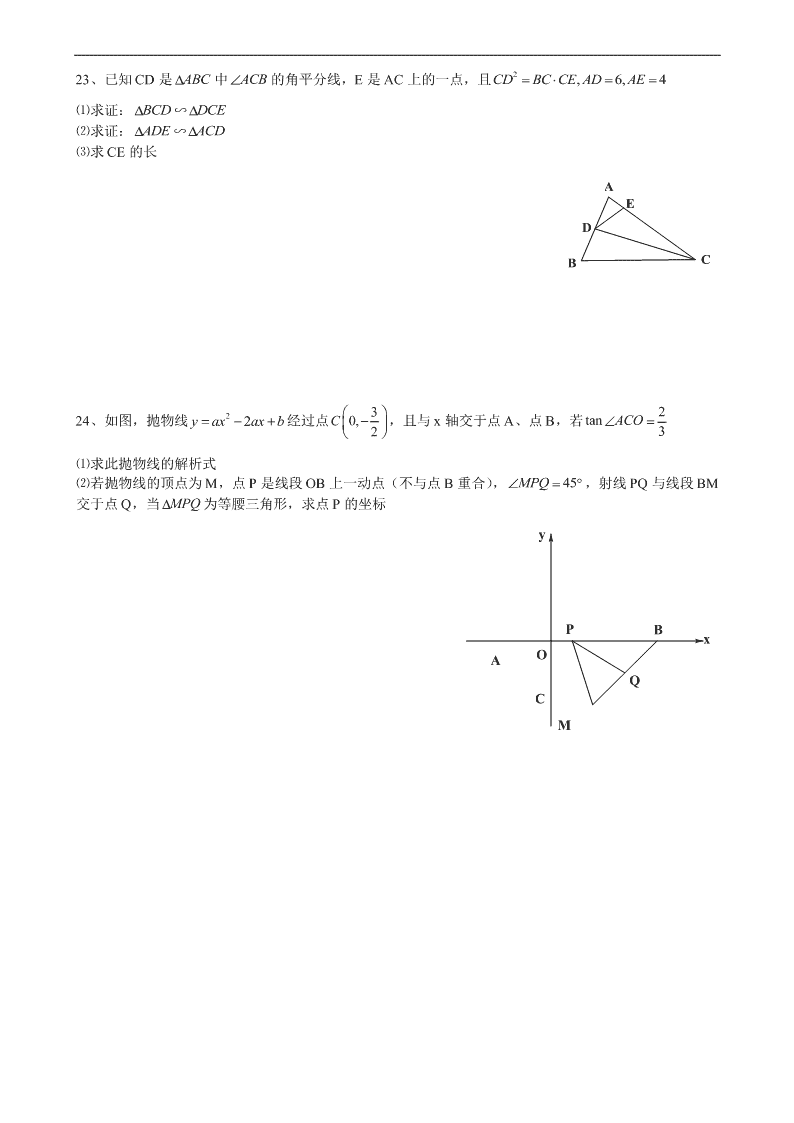 21、如图，在 ABC 中， 90 ,ACB AC BC    ,点 P 是 形内一点，且 135APB APC     ⑴求证： CPA APB∽ ⑵试求 tan PCB 的值 22、如图，浦西对岸的高楼 AB，在 C 处测得楼顶 A 的倾角为30 ，向高楼前进 100 米到达 D 处，在 D 处 测得 A 的仰角为 45，求高楼 AB 的高 D CB A P C B A BDC A 23、已知 CD 是 ABC 中 ACB 的角平分线，E 是 AC 上的一点，且 2 , 6, 4CD BC CE AD AE    ⑴求证： BCD DCE∽ ⑵求证： ADE ACD∽ ⑶求 CE 的长 24、如图，抛物线 2 2y ax ax b   经过点 30, 2C ，且与 x 轴交于点 A、点 B，若 2tan 3ACO ⑴求此抛物线的解析式 ⑵若抛物线的顶点为 M，点 P 是线段 OB 上一动点（不与点 B 重合）， 45MPQ  ，射线 PQ 与线段 BM 交于点 Q，当 MPQ 为等腰三角形，求点 P 的坐标 E B D C A P xB Q M C OA y 25、如图，在正方形 ABCD 中， 2AB  ，点 P 是边 BC 上的任意一点，E 是 BC 延长线上一点，联结 AP 作 PF AP 交 DCE 的平分线 CF 上一点 F，联结 AF 交边 CD 于点 G ⑴求证： AP PF ⑵设点 P 到 B 的距离为 x,线段 DG 的长为 y 试求 y 与 x 的函数关系式，并写出自变量 x 的取值范围 ⑶当点 P 是线段 BC 延长线上一动点，那么⑵式中 y 与 x 的函数关系式保持不变吗？如改变，试直接写出 函数关系式 E F CPB G DA 2013 学年普陀区九年级数学期终调研试卷 参考答案及评分说明 一、选择题（本大题共 6 题，每题 4 分，满分 24 分） 1．(B)； 2． (B)； 3．(A)； 4．(A)； 5．(D)； 6．(C)． 二、填空题（本大题共 12 题，每题 4 分，满分 48 分） 7．2； 8． 1∶ 4 3 ； 9． 2 1yx   ； 10． 2( 2)yx   等； 11． 11 22ba ； 12． △PAB∽△PCA； 13． 30°； 14． 1 ； 15． 2； 16. 22( 2) 3yx    ； 17． 6 或 12 或 10； 18． 22 或 12． 三、解 答题：（本大题共 7 题，满分 78 分） 19.解：原式 3 3 132 3 2 (1 2 1) 3        ……………………………………………………………（5 分） 3 3   …………………………………………………………………………（3 分） 1 ． ………………………………………………………… ……………（2 分） 20. 解：(1) 3( 2 ) ( 3 )2a b a b     = 3232a b a b    …………………（2 分） = 1 2ab ．……………………………（2 分） ∴ BE 就是所求的向量， = ． （不在原图上作，正确，不扣分） （画图 2 分，结论 1 分） （2） 1()3BD BC CD b a b     ………………………………………………（2 分） = 12 33ab ．………………………………………………………………（1 分） （ （第 20 题） （ A （ B （ C （ D E a 1 2 b 21.(1)证明：∵∠APB=∠APC=135°，…………………（1 分） 又∵AC=BC，∠ACB=90°， ∴∠1+∠3=45°，…………………………（1 分） ∠2+∠3=45°，…………………………（1 分） ∴∠2=∠1．…………………………………（1 分） ∴△APB∽△CPA．…………………………（2 分） (2)解：∵△APB∽△CPA， ∴ 2AB PA PB CA CP PA   ，………………………（1 分） ∴ 2PB PA ， 2 2PC PA ．……………………………………………………（2 分） 在△PBC 中，∵∠CPB=90°， tan∠PCB= PB PC =2．…………………………………………………………………（1 分） 22．解：由题意得：AB⊥CB，∠C=30°，∠ADB=45°,CD=100m．…………………（4 分） 在 Rt△ADB 中，∵∠ADB=∠DAB =45°, ∴DB=AB．……………………………………………………（1 分） 在 Rt△ACB 中，∵∠ABC =90°,∠C=30°, ∴tan30°= AB BC ，……………………………………………（1 分） ∴ 1 100 3 AB AB  ，……………………………………………（1 分） ∴ 3 100AB AB，………………………………………（1 分） 解得： 50( 3 1)AB ．……………………………………………（1 分） 答：高楼 AB 的高为50( 3 1) 米．…………………………………………………（1 分） 23． (1)证明：∵CD 是△ABC 中∠ACB 的角平分线， ∴∠1=∠2；……………………………………（1 分） ∵ 2CD BC CE， ∴ CD CE CB CD ；…………………………………（1 分） ∴△DCE∽△BCD．……………………………（1 分） (2)证明：∵△DCE∽△BCD． ∴∠4=∠B；………………………………………………………………………（1 分） ∵∠4+∠3=∠2+∠B， ∴∠3=∠2；………………………………………………………………………（1 分） ∴∠3=∠1；………………………………………………………………………（1 分） 又∵∠A=∠A，………………………………………………………………………（1 分） （ （第 21 题） （ A （ B （ C （ P 1 3 2 1 A B C D E 2 3 4 第 23 题 ∴△ADE∽△ACD．………………………………………………………………（1 分） (3)解：∵△ADE∽△ACD， ∴ AE AD AD AC ，………………………………………………………………………（1 分） ∵AD=6，AE=4， ∴ 46 64CE  ，……………………………………………………………………（1 分） 解得 CE=5． 所以 CE 的长为 5．…………………………………………………………………（2 分） 24. 解：(1)∵抛物线 2 1 2y ax ax b   经过点 C（0， 3 2 ）， ∴b= ，OC= 3 2 ．……………………………………………………………（1 分） ∵∠AOC=90°，tan∠ACO= 2 3 ， ∴OA= OC=1，∴点 A 坐标为（ 1 ，0）， …………………………………（1 分） 代入解析式，解得 a= 1 2 ， 所以解析式为： 213 22y x x   ．……………………………………………（1 分） (2) 由 解得：M（1， 2 ）， B（3，0）． ……………………………………………（2 分） 过点 M 作 MD⊥x 轴交于点 D，…………（1 分） ∵DM=DB=2， ∴∠OBM=45°． ………………………（1 分） ①当 QP=QM 时， ∠QPM=∠QMP=45°，∴∠PQM=90°． 又∵∠OBM=45°，∴∠MPB=90°． ∴P（1，0）．………………………………（1 分） ②当 PM=PQ 时， ∵∠MPQ=∠OBM =45°，∠PMQ=∠BMP， ∴△PMQ∽△BMP，…………………………………………………………（1 分） ∴BP= BM= 22，……………………………………………………………（1 分） ∴P（3 2 2 ，0）．…………………………………………………………（1 分） ③当 MP=MQ 时， 点 Q 与点 B 重合，点 P 与点 A 重合，不合题意，舍去．…………………（1 分） 综上所述，符合条件的点 P 坐标为（1，0）或（ ，0）． x （ （第 24 题） M A C B O y P Q D 25.解：(1)在 AB 上截取 AQ=PC，联结 PQ．……………………………………………（1 分） ∵四边形 ABCD 为正方形，∴AB=BC，∠B=∠DCE=90°． ∵点 P 在 BC 上，BQ=BP，∴∠1=∠2=45°． 又∵CF 是∠DCE 的平分线， ∴∠FCD=45°，∴∠AQP=∠PCF=135°．…（1 分） ∵PF⊥AP，∴∠APB+∠3=∠APB+∠4=90°． ∴∠3=∠4．………………………………………（1 分） ∴△QAP≌△CPF，………………………………（1 分） ∴AP=PF．…………………………………………（1 分） (2) 过点 F 作 FM⊥CE，垂足为 M，…………………………………………………（1 分） ∵∠B=∠FMP=90°，又∵∠3=∠4，AP=PF ， ∴△ABP≌△PMF．………………………………………………………………（1 分） ∴BP=MF． 过点 F 作 FN⊥CD，垂足为 N，…………………………………………………（1 分） ∵CF 是∠DCE 的平分线，∴FM=FN， ∴四边形 CMFN 是正方形． ∴CN=NF=FM=BP=x，DN=2–x． ∵DG=y，GN=2–x–y．…………………………………………………………（1 分） ∵AD∥NF， ∴ AD DG NF GN ， ∴ 2 2 y x x y ，…………………………………………………………………（1 分） ∴ 42 2 xy x   ， (0≤x< 2) ．……………………………………………………（2 分） (3) 24 2 xy x   ，(x> 2) ．…………………………………………………………………（2 分） A B C D M F G P (第 25 题) Q 1 2 3 4 E N