海南省2012年中考数学模拟试题 6页

海南省2012年中考数学模拟试题 ‎（考试时间100分钟，本卷满分110分）‎ 一、选择题（本题满分42分，每小题3分）‎ ‎1.-5的相反数是 （ ） ‎ ‎ A． B． C． D．5 ‎ ‎2.下列运算中，结果正确的是（ ）‎ A．2a+3b=5ab B．2a-(a+b)=a-b C．(a+b)2=a2+b2 D．a2 ·a3=a 6‎ ‎3.右图1所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是（ ） ‎ 图1‎ ‎ A. B. C. D.‎ ‎4.海南岛首条高铁客运专线——东环高速铁路全长308110米，途经海口市、文昌市、琼海市、万宁市、陵水黎族自治县、三亚市.数据308110米用科学记数法表示应为（保留两个有效数字）（ ）‎ ‎ A、3.1×104米 B、3.1×105米 C、3.1×106米 D、3.1×107米 ‎5.使分式有意义的x的取值是（ ） ‎ A． 　B．　　 C．x = 　D．x =　‎ ‎6.如图2，直线EF分别与直线AB、CD相交于点G、H，已知∠1=∠2=50°，GM平分 ‎∠HGB交直线CD于点M．则∠3的度数为（ ）‎ A．60 B．65 C．70 D．130‎ 图4‎ 图2‎ A B C 图3‎ A B C D O A B G C D M H F ‎1‎ ‎2‎ ‎3‎ ‎ ‎ ‎7.在正方形网格中，△ABC位置如图3所示，则sin∠ABC的值为（ ） ‎ A. B. C. D. 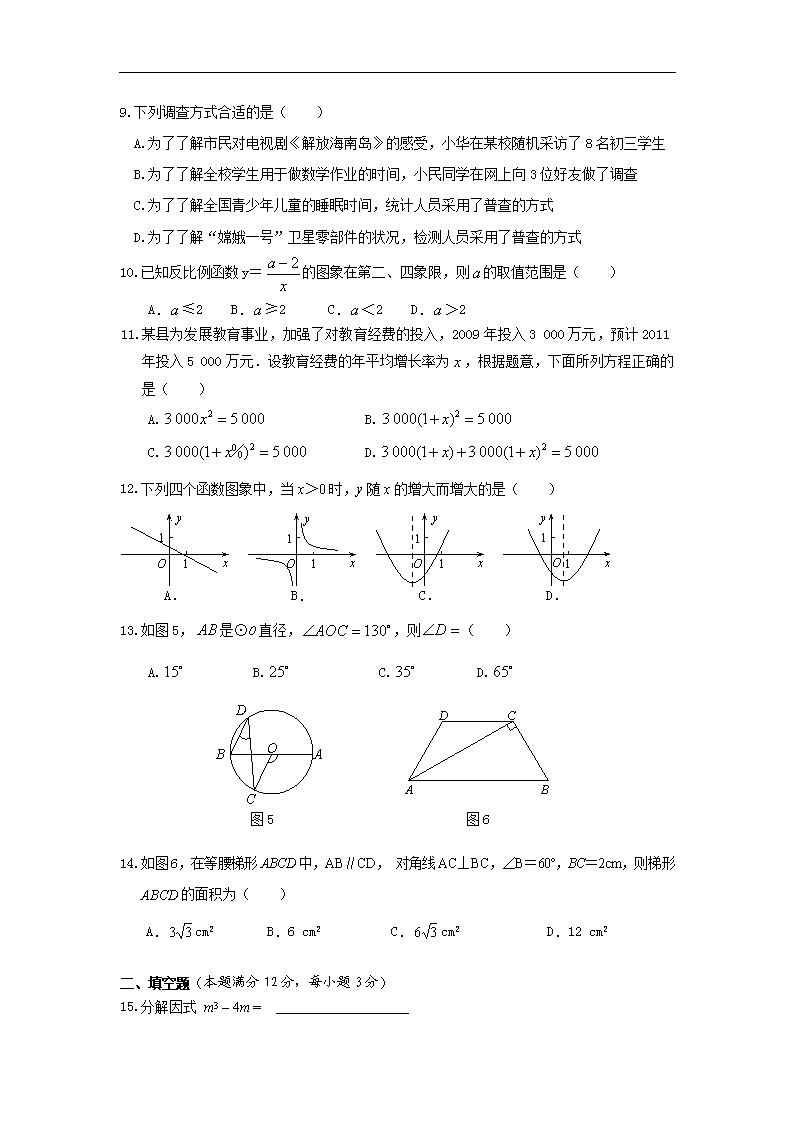‎ ‎8.如图4，已知□ABCD的对角线BD=4cm，将□ABCD绕其对称中心O旋转180°，则点D所转过的路径长为（ ） ‎ A．4π cm B．3π cm C．2π cm D．π cm ‎9.下列调查方式合适的是（ ）‎ A.为了了解市民对电视剧《解放海南岛》的感受，小华在某校随机采访了8名初三学生 B.为了了解全校学生用于做数学作业的时间，小民同学在网上向3位好友做了调查 C.为了了解全国青少年儿童的睡眠时间，统计人员采用了普查的方式 D.为了了解“嫦娥一号”卫星零部件的状况，检测人员采用了普查的方式 ‎10.已知反比例函数y＝的图象在第二、四象限，则的取值范围是（ ） ‎ A．≤2 B．≥2 C．＜2 D．＞2‎ ‎11.某县为发展教育事业，加强了对教育经费的投入，2009年投入3 000万元，预计2011年投入5 000万元．设教育经费的年平均增长率为，根据题意，下面所列方程正确的是（ ）‎ A. B.‎ C. D.‎ ‎12.下列四个函数图象中，当x＞0时，y随x的增大而增大的是（ ）‎ O y x ‎1‎ ‎1‎ A．‎ O y x ‎1‎ ‎1‎ C．‎ O y x ‎1‎ ‎1‎ D．‎ O y x ‎1‎ ‎1‎ B．‎ ‎13.如图5，是⊙O直径，，则（ ） ‎ A. B. C. 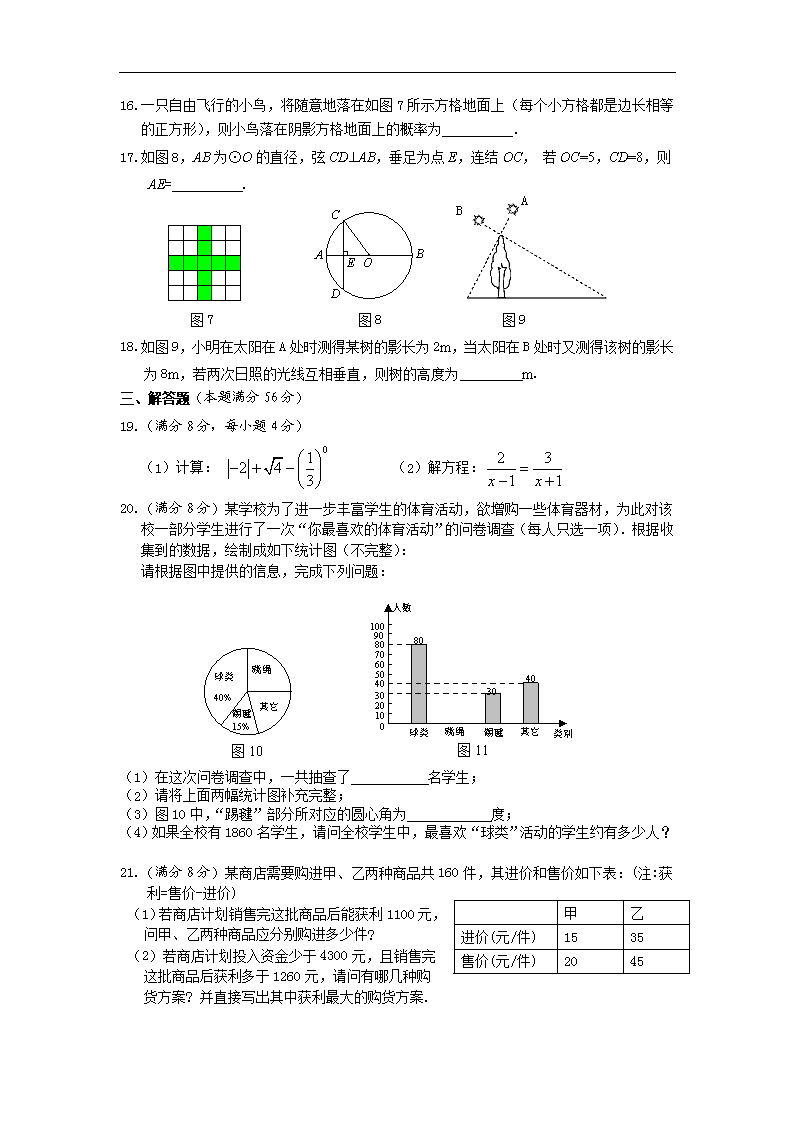D.‎ A C B D D B O A C 图6‎ 图5‎ ‎14.如图6，在等腰梯形ABCD中，AB∥CD， 对角线AC⊥BC，∠B＝60º，BC＝‎2cm，则梯形ABCD的面积为（ ） ‎ ‎ A．cm2 B．‎6 cm2 C．cm2 D．‎12 cm2‎ 二、填空题（本题满分12分，每小题3分）‎ ‎15.分解因式 m3 – ‎4m = ‎ ‎16.一只自由飞行的小鸟，将随意地落在如图7所示方格地面上（每个小方格都是边长相等的正方形），则小鸟落在阴影方格地面上的概率为 ．‎ A B ‎17.如图8，AB为⊙O的直径，弦CD^AB，垂足为点E，连结OC， 若OC=5，CD=8，则AE= .‎ O A B C D E 图9‎ 图8‎ 图7‎ ‎18.如图9，小明在太阳在A处时测得某树的影长为‎2m，当太阳在B处时又测得该树的影长为‎8m，若两次日照的光线互相垂直，则树的高度为 m.‎ 三、解答题（本题满分56分）‎ ‎19.（满分8分，每小题4分）‎ ‎（1）计算： （2）解方程：‎ ‎20.（满分8分）某学校为了进一步丰富学生的体育活动，欲增购一些体育器材，为此对该校一部分学生进行了一次“你最喜欢的体育活动”的问卷调查（每人只选一项）．根据收 集到的数据，绘制成如下统计图（不完整）：‎ 请根据图中提供的信息，完成下列问题：‎ ‎100‎ ‎90‎ ‎80‎ ‎70‎ ‎60‎ ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ ‎0‎ 球类 跳绳 踢毽 其它 类别 ‎30‎ ‎40‎ ‎80‎ 人数 图11‎ 图10‎ 球类 ‎40%‎ 跳绳 其它 踢毽15%‎ ‎ ‎ ‎（1）在这次问卷调查中，一共抽查了 名学生；‎ ‎（2）请将上面两幅统计图补充完整；‎ ‎（3）图10中，“踢毽”部分所对应的圆心角为 度；‎ ‎（4）如果全校有1860名学生，请问全校学生中，最喜欢“球类”活动的学生约有多少人？‎ ‎21.（满分8分）某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：(注:获利=售价-进价)‎ 甲 乙 进价(元/件)‎ ‎15‎ ‎35‎ 售价(元/件)‎ ‎20‎ ‎45‎ ‎（1）若商店计划销售完这批商品后能获利1100元， 问甲、乙两种商品应分别购进多少件?‎ ‎（2）若商店计划投入资金少于4300元，且销售完这批商品后获利多于1260元，请问有哪几种购货方案? 并直接写出其中获利最大的购货方案.‎ O x y A C B ‎22.（满分8分）如图12，已知的三个顶点的坐标分别为、、．‎ ‎（1）请直接写出点关于轴对称的点的坐标；‎ ‎（2）将绕坐标原点逆时针旋转 ‎90°．画出图形，直接写出点的对应点的坐标；‎ ‎（3）请直接写出：以为顶点的 平行四边形的第四个顶点的坐标．‎ 图12‎ ‎23.(满分11分）如图13，四边形ABCD是边长为a的正方形，点G，E分别是边AB，BC的中点，∠AEF=90o，且EF交正方形外角的平分线CF于点F．‎ ‎ （1）证明：∠BAE=∠FEC；‎ ‎（2）证明：△AGE≌△ECF；‎ 图13‎ ‎（3）求△AEF的面积．‎ ‎24.(满分13分)如图14，已知二次函数的图象经过点．‎ ‎(1)求此函数的解析式及图象的对称轴；‎ x y O A B C P Q M N 图14‎ ‎(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动，点Q从O点出发以相同的速度沿线段OA向A点运动，其中一个动点到达端点时，另一个也随之停止运动．设运动时间为t秒．‎ ‎①当t为何值时，四边形ABPQ为等腰梯形；‎ ‎②设PQ与对称轴的交点为M，过M点作 x轴的平行线交AB于点N，设四边形ANPQ 的面积为S，求面积S关于时间t的函数解析式，‎ 并指出t的取值范围；当t为何值时，‎ S有最大值或最小值．‎ 参考答案 一、选择题 DBABA BCCDC BCBA 二、填空题 ‎15. m(m+2)(m-2) 16. 17. 2 18.4‎ 三、解答题 ‎19.(1)3 (2)x=5 ‎ ‎20.(1)200 (2)图略 (3)54 (4)744人 ‎21. 解：（1）设甲种商品应购进x件，乙种商品应购进y件.‎ ‎ 根据题意，得 解得： ‎ 答：甲种商品购进100件，乙种商品购进60件. ‎ ‎（2）设甲种商品购进a件，则乙种商品购进(160-a)件.‎ 根据题意，得 ‎ 解不等式组，得 65＜a＜68 . ‎ ‎∵a为非负整数，∴a取66，67.‎ ‎∴ 160-a相应取94，93. ‎ 答：有两种构货方案，方案一：甲种商品购进66件，乙种商品购进94件；方案二：甲种商品购进67件，乙种商品购进93件.其中获利最大的是方案一. ‎ ‎22.解：（1）（2，3）； （2）图形略．（0，）；‎ ‎（3）（-7，3）或（-5，-3）或（3，3）‎ ‎23. （1）证明：∵∠AEF=90o， ‎ ‎∴∠FEC+∠AEB=90o．‎ 在Rt△ABE中，∠AEB+∠BAE=90o，‎ ‎∴∠BAE=∠FEC；‎ ‎（2）证明：∵G，E分别是正方形ABCD的边AB，BC的中点，‎ ‎∴AG=GB=BE=EC，且∠AGE=180o－45o=135o．‎ 又∵CF是∠DCH的平分线，‎ ‎ ∠ECF=90o+45o=135o．‎ 在△AGE和△ECF中，‎ ‎ ‎ ‎ ∴△AGE≌△ECF； ‎ ‎ （3）解：由△AGE≌△ECF，得AE=EF．‎ 又∵∠AEF=90o，‎ ‎∴△AEF是等腰直角三角形．‎ 由AB=a，BE=a，知AE=a，∴S△AEF=a2．‎ x y O A B C P Q D E G M N F ‎24.解：(1)将点A(3，0)，B(2，-3), C(0，-3)代入得 解得a=1，b=-2, c =-3‎ ‎∴．‎ 配方得：，所以对称轴为直线x=1．‎ ‎(2) 由题意可知：BP= OQ=0.1t．‎ ‎∵点B，点C的纵坐标相等，‎ ‎∴BC∥OA．‎ 过点B，点P作BD⊥OA，PE⊥OA，垂足分别为D，E．‎ 要使四边形ABPQ为等腰梯形，只需PQ=AB．‎ 即QE=AD=1．又QE=OE－OQ=(2-0.1t)-0.1t=2-0.2t，‎ ‎∴2-0.2t=1．解得t=5．即t=5秒时，四边形ABPQ为等腰梯形．‎ ‎②设对称轴与BC，x轴的交点分别为F，G．‎ ‎∵对称轴x=1是线段BC的垂直平分线，∴BF=CF=OG=1．‎ 又∵BP=OQ，∴PF=QG．‎ 又∵∠PMF=∠QMG，∴△MFP≌△MGQ．‎ ‎∴MF=MG．∴点M为FG的中点 ‎ ‎∴S==．‎ 由=．． ‎ ‎ ∴S=．又BC=2，OA=3，‎ ‎∴点P运动到点C时停止运动，需要20秒．‎ ‎∴0