2013年甘肃省白银市中考数学试题（含答案） 17页

甘肃省白银市2013年中考数学试卷 ‎　‎ 一、选择题：本大题共10小题，每小题3分，共30分．每小题给出的四个选项中，只有一项是符合题目要求的，请将符合题意的选项字母填入题后的括号内 ‎1．（3分）（2012•绍兴）3的相反数是（　　）‎ ‎　‎ A．‎ ‎3‎ B．‎ ‎﹣3‎ C．‎ D．‎ ‎﹣‎ 考点：‎ 相反数．‎ 分析：‎ 根据相反数的意义，3的相反数即是在3的前面加负号．‎ 解答：‎ 解：根据相反数的概念及意义可知：3的相反数是﹣3．‎ 故选B．‎ 点评：‎ 本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“﹣”号；一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．‎ ‎　‎ ‎2．（3分）（2013•白银）下列运算中，结果正确的是（　　）‎ ‎　‎ A．‎ ‎4a﹣a=3a B．‎ a10÷a2=a5‎ C．‎ a2+a3=a5‎ D．‎ a3•a4=a12‎ 考点：‎ 同底数幂的除法；合并同类项；幂的乘方与积的乘方．‎ 专题：‎ 计算题．‎ 分析：‎ 根据合并同类项、同底数幂的除法法则：底数不变，指数相减，同底数幂的乘法法则：底数不变，指数相加，可判断各选项．‎ 解答：‎ 解：A、4a﹣a=3a，故本选项正确；‎ B、a10÷a2=a10﹣2=a8≠a5，故本选项错误；‎ C、a2+a3≠a5，故本选项错误；‎ D、根据a3•a4=a7，故a3•a4=a12本选项错误；‎ 故选A．‎ 点评：‎ 此题考查了同类项的合并，同底数幂的乘除法则，属于基础题，解答本题的关键是掌握每部分的运算法则，难度一般．‎ ‎　‎ ‎3．（3分）（2011•桂林）下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽，其中为中心对称图形的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 中心对称图形．‎ 分析：‎ 根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，即可判断出．‎ 解答：‎ 解：∵A．此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，故此选项错误；‎ B：∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，故此选项错误；‎ C．此图形旋转180°后能与原图形重合，此图形是中心对称图形，故此选项正确；‎ D：∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，故此选项错误．‎ 故选C．‎ 点评：‎ 此题主要考查了中心对称图形的定义，根据定义得出图形形状是解决问题的关键．‎ ‎　‎ ‎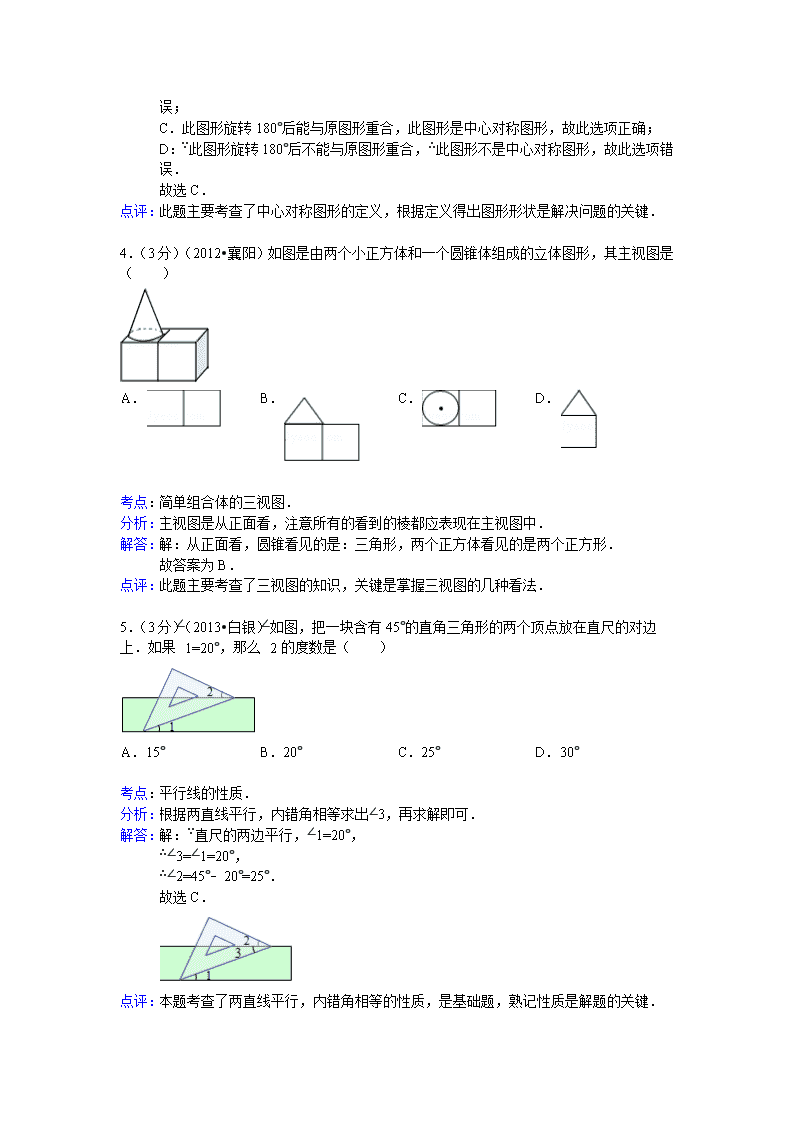4．（3分）（2012•襄阳）如图是由两个小正方体和一个圆锥体组成的立体图形，其主视图是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 简单组合体的三视图．‎ 分析：‎ 主视图是从正面看，注意所有的看到的棱都应表现在主视图中．‎ 解答：‎ 解：从正面看，圆锥看见的是：三角形，两个正方体看见的是两个正方形．‎ 故答案为B．‎ 点评：‎ 此题主要考查了三视图的知识，关键是掌握三视图的几种看法．‎ ‎　‎ ‎5．（3分）（2013•白银）如图，把一块含有45°的直角三角形的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）‎ ‎　‎ A．‎ ‎15°‎ B．‎ ‎20°‎ C．‎ ‎25°‎ D．‎ ‎30°‎ 考点：‎ 平行线的性质．‎ 分析：‎ 根据两直线平行，内错角相等求出∠3，再求解即可．‎ 解答：‎ 解：∵直尺的两边平行，∠1=20°，‎ ‎∴∠3=∠1=20°，‎ ‎∴∠2=45°﹣20°=25°．‎ 故选C．‎ 点评：‎ 本题考查了两直线平行，内错角相等的性质，是基础题，熟记性质是解题的关键．‎ ‎　‎ ‎6．（3分）（2008•包头）一元二次方程x2+x﹣2=0根的情况是（　　）‎ ‎　‎ A．‎ 有两个不相等的实数根 B．‎ 有两个相等的实数根 ‎　‎ C．‎ 无实数根 D．‎ 无法确定 考点：‎ 根的判别式．‎ 分析：‎ 判断上述方程的根的情况，只要看根的判别式△=b2﹣4ac的值的符号就可以了．‎ 解答：‎ 解：∵a=1，b=1，c=﹣2，‎ ‎∴△=b2﹣4ac=1+8=9＞0‎ ‎∴方程有两个不相等的实数根．‎ 故选A 点评：‎ 本题考查了一元二次方程根的判别式的应用．‎ 总结：一元二次方程根的情况与判别式△的关系：‎ ‎（1）△＞0⇔方程有两个不相等的实数根；‎ ‎（2）△=0⇔方程有两个相等的实数根；‎ ‎（3）△＜0⇔方程没有实数根．‎ ‎　‎ ‎7．（3分）（2012•广西）分式方程的解是（　　）‎ ‎　‎ A．‎ x=﹣2‎ B．‎ x=1‎ C．‎ x=2‎ D．‎ x=3‎ 考点：‎ 解分式方程．‎ 分析：‎ 公分母为x（x+3），去括号，转化为整式方程求解，结果要检验．‎ 解答：‎ 解：去分母，得x+3=2x，‎ 解得x=3，‎ 当x=3时，x（x+3）≠0，‎ 所以，原方程的解为x=3，‎ 故选D．‎ 点评：‎ 本题考查了解分式方程．（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解，（2）解分式方程一定注意要验根．‎ ‎　‎ ‎8．（3分）（2013•白银）某超市一月份的营业额为36万元，三月份的营业额为48万元，设每月的平均增长率为x，则可列方程为（　　）‎ ‎　‎ A．‎ ‎48（1﹣x）2=36‎ B．‎ ‎48（1+x）2=36‎ C．‎ ‎36（1﹣x）2=48‎ D．‎ ‎36（1+x）2=48‎ 考点：‎ 由实际问题抽象出一元二次方程．‎ 专题：‎ 增长率问题．‎ 分析：‎ 三月份的营业额=一月份的营业额×（1+增长率）2，把相关数值代入即可．‎ 解答：‎ 解：二月份的营业额为36（1+x），‎ 三月份的营业额为36（1+x）×（1+x）=36（1+x）2，‎ 即所列的方程为36（1+x）2=48，‎ 故选D．‎ 点评：‎ 考查列一元二次方程；得到三月份的营业额的关系是解决本题的关键．‎ ‎　‎ ‎9．（3分）（2013•白银）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：‎ ‎①2a﹣b＜0；②abc＜0；③a+b+c＜0；④a﹣b+c＞0；⑤4a+2b+c＞0，‎ 错误的个数有（　　）‎ ‎　‎ A．‎ ‎1个 B．‎ ‎2个 C．‎ ‎3个 D．‎ ‎4个 考点：‎ 二次函数图象与系数的关系．‎ 分析：‎ 由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，利用图象将x=1，﹣1，2代入函数解析式判断y的值，进而对所得结论进行判断．‎ 解答：‎ 解：①∵由函数图象开口向下可知，a＜0，由函数的对称轴x=﹣＜0，故b＞0，所以2a﹣b＜0，①正确； ‎ ‎②∵a＜0，对称轴在y轴左侧，a，b同号，图象与y轴交于负半轴，则c＜0，故abc＜0；②正确；‎ ‎③当x=1时，y=a+b+c＜0，③正确；‎ ‎④当x=﹣1时，y=a﹣b+c＜0，④错误；‎ ‎⑤当x=2时，y=4a+2b+c＜0，⑤错误；‎ 故错误的有2个．‎ 故选：B．‎ 点评：‎ 此题主要考查了图象与二次函数系数之间的关系，将x=1，﹣1，2代入函数解析式判断y的值是解题关键．‎ ‎　‎ ‎10．（3分）（2010•岳阳）如图，⊙O的圆心在定角∠α（0°＜α＜180°）的角平分线上运动，且⊙O与∠α的两边相切，图中阴影部分的面积S关于⊙O的半径r（r＞0）变化的函数图象大致是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 动点问题的函数图象；多边形内角与外角；切线的性质；切线长定理；扇形面积的计算；锐角三角函数的定义．‎ 专题：‎ 计算题．‎ 分析：‎ 连接OB、OC、OA，求出∠BOC的度数，求出AB、AC的长，求出四边形OBAC和扇形OBC的面积，即可求出答案．‎ 解答：‎ 解：连接OB、OC、OA，‎ ‎∵圆O切AM于B，切AN于C，‎ ‎∴∠OBA=∠OCA=90°，OB=OC=r，AB=AC ‎∴∠BOC=360°﹣90°﹣90°﹣α=（180﹣α）°，‎ ‎∵AO平分∠MAN，‎ ‎∴∠BAO=∠CAO=α，‎ AB=AC=，‎ ‎∴阴影部分的面积是：S四边形BACO﹣S扇形OBC=2×××r﹣=（﹣）r2，‎ ‎∵r＞0，‎ ‎∴S与r之间是二次函数关系．‎ 故选C．‎ 点评：‎ 本题主要考查对切线的性质，切线长定理，三角形和扇形的面积，锐角三角函数的定义，四边形的内角和定理等知识点的理解和掌握，能综合运用性质进行计算是解此题的关键．‎ ‎　‎ 二、填空题：本大题共8小题，每小题4分，共32分，把答案写在题中的横线上 ‎11．（4分）（2011•连云港）分解因式：x2﹣9=　（x+3）（x﹣3）　．‎ 考点：‎ 因式分解-运用公式法．‎ 分析：‎ 本题中两个平方项的符号相反，直接运用平方差公式分解因式．‎ 解答：‎ 解：x2﹣9=（x+3）（x﹣3）．‎ 点评：‎ 主要考查平方差公式分解因式，熟记能用平方差公式分解因式的多项式的特征，即“两项、异号、平方形式”是避免错用平方差公式的有效方法．‎ ‎　‎ ‎12．（4分）（2012•广安）不等式2x+9≥3（x+2）的正整数解是　1，2，3　．‎ 考点：‎ 一元一次不等式的整数解．‎ 专题：‎ 计算题．‎ 分析：‎ 先解不等式，求出其解集，再根据解集判断其正整数解．‎ 解答：‎ 解：2x+9≥3（x+2），‎ 去括号得，2x+9≥3x+6，‎ 移项得，2x﹣3x≥6﹣9，‎ 合并同类项得，﹣x≥﹣3，‎ 系数化为1得，x≤3，‎ 故其正整数解为1，2，3．‎ 点评：‎ 本题考查了一元一次不等式的整数解，会解不等式是解题的关键．‎ ‎　‎ ‎13．（4分）（2012•随州）等腰三角形的周长为16，其一边长为6，则另两边为　6，4或5，5　．‎ 考点：‎ 等腰三角形的性质；三角形三边关系．‎ 分析：‎ 此题分为两种情况：6是等腰三角形的腰或6是等腰三角形的底边．然后进一步根据三角形的三边关系进行分析能否构成三角形．‎ 解答：‎ 解：当腰是6时，则另两边是4，6，且4+6＞6，满足三边关系定理；‎ 当底边是6时，另两边长是5，5，5+5＞6，满足三边关系定理，‎ 故该等腰三角形的另两边为：6，4或5，5．‎ 故答案为：6，4或5，5．‎ 点评：‎ 本题考查了等腰三角形的性质，应从边的方面考查三角形，涉及分类讨论的思想方法，难度适中．‎ ‎　‎ ‎14．（4分）（2009•朝阳）如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O）20米的A处，则小明的影子AM长为　5　米．‎ 考点：‎ 相似三角形的应用．‎ 分析：‎ 易得：△ABM∽△OCM，利用相似三角形的相似比可得出小明的影长．‎ 解答：‎ 解：根据题意，易得△MBA∽△MCO，‎ 根据相似三角形的性质可知=，即=，‎ 解得AM=5m．则小明的影长为5米．‎ 点评：‎ 本题只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比可得出小明的影长．‎ ‎　‎ ‎15．（4分）（2013•白银）如图，已知BC=EC，∠BCE=∠ACD，要使△ABC≌△DEC，则应添加的一个条件为　AC=CD　．（答案不唯一，只需填一个）‎ 考点：‎ 全等三角形的判定．‎ 专题：‎ 开放型．‎ 分析：‎ 可以添加条件AC=CD，再由条件∠BCE=∠ACD，可得∠ACB=∠DCE，再加上条件CB=EC，可根据SAS定理证明△ABC≌△DEC．‎ 解答：‎ 解：添加条件：AC=CD，‎ ‎∵∠BCE=∠ACD，‎ ‎∴∠ACB=∠DCE，‎ 在△ABC和△DEC中，‎ ‎∴△ABC≌△DEC（SAS），‎ 故答案为：AC=CD（答案不唯一）．‎ 点评：‎ 此题主要考查了考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．‎ 注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．‎ ‎　‎ ‎16．（4分）（2012•温州）若代数式的值为零，则x=　3　．‎ 考点：‎ 分式的值为零的条件；解分式方程．‎ 专题：‎ 计算题．‎ 分析：‎ 由题意得=0，解分式方程即可得出答案．‎ 解答：‎ 解：由题意得，=0，‎ 解得：x=3，经检验的x=3是原方程的根．‎ 故答案为：3．‎ 点评：‎ 此题考查了分式值为0的条件，属于基础题，注意分式方程需要检验．‎ ‎　‎ ‎17．（4分）（2012•盐城）已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根，且O1O2=t+2，若这两个圆相切，则t=　2或0　．‎ 考点：‎ 圆与圆的位置关系；解一元二次方程-因式分解法．‎ 分析：‎ 先解方程求出⊙O1、⊙O2的半径，再分两圆外切和两圆内切两种情况列出关于t的方程讨论求解．‎ 解答：‎ 解：∵⊙O1、⊙O2的半径分别是方程x2﹣4x+3=0的两根，‎ 解得⊙O1、⊙O2的半径分别是1和3．‎ ‎①当两圆外切时，圆心距O1O2=t+2=1+3=4，解得t=2；‎ ‎②当两圆内切时，圆心距O1O2=t+2=3﹣1=2，解得t=0．‎ ‎∴t为2或0．‎ 故答案为：2或0．‎ 点评：‎ 考查解一元二次方程﹣因式分解法和圆与圆的位置关系，同时考查综合应用能力及推理能力．注意：两圆相切，应考虑内切或外切两种情况是解本题的难点．‎ ‎　‎ ‎18．（4分）（2013•白银）现定义运算“★”，对于任意实数a、b，都有a★b=a2﹣3a+b，如：3★5=32﹣3×3+5，若x★2=6，则实数x的值是　﹣1或4　．‎ 考点：‎ 解一元二次方程-因式分解法．‎ 专题：‎ 新定义．‎ 分析：‎ 根据题中的新定义将所求式子转化为一元二次方程，求出一元二次方程的解即可得到x的值．‎ 解答：‎ 解：根据题中的新定义将x★2=6变形得：‎ x2﹣3x+2=6，即x2﹣3x﹣4=0，‎ 因式分解得：（x﹣4）（x+1）=0，‎ 解得：x1=4，x2=﹣1，‎ 则实数x的值是﹣1或4．‎ 故答案为：﹣1或4‎ 点评：‎ 此题考查了解一元二次方程﹣因式分解法，利用此方法解方程时，首先将方程右边化为0，左边变为积的形式，然后根据两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．‎ ‎　‎ 三、解答题（一）：本大题共5小题，共38分，解答时，应写出必要的文字说明、证明过程或演算步骤。‎ ‎19．（6分）（2012•广元）计算：2cos45°﹣（﹣）﹣1﹣﹣（π﹣）0．‎ 考点：‎ 实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．‎ 专题：‎ 计算题．‎ 分析：‎ 根据45°角的余弦等于，有理数的负整数指数次幂等于正整数指数次幂的倒数，二次根式的化简，任何非0数的0次幂等于1进行计算即可得解．‎ 解答：‎ 解：2cos45°﹣（﹣）﹣1﹣﹣（π﹣）0，‎ ‎=2×﹣（﹣4）﹣2﹣1，‎ ‎=+4﹣2﹣1，‎ ‎=3﹣．‎ 点评：‎ 本题考查了实数的运算，主要利用了特殊角的三角函数值，负整数指数幂，二次根式的化简，零指数幂，是基础运算题，注意运算符号的处理．‎ ‎　‎ ‎20．（6分）（2011•朝阳）先化简，再求值：，其中x=﹣．‎ 考点：‎ 分式的化简求值．‎ 专题：‎ 计算题．‎ 分析：‎ 先通分计算括号里的，再把除法转化成乘法进行约分，最后把x的值代入计算即可．‎ 解答：‎ 解：原式=•=x﹣1，‎ 当x=﹣时，原式=﹣﹣1=﹣．‎ 点评：‎ 本题考查了分式的化简求值，解题的关键是注意把分式的分子、分母因式分解．‎ ‎　‎ ‎21．（8分）（2013•白银）两个城镇A、B与两条公路l1、l2位置如图所示，电信部门需在C处修建一座信号反射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路l1，l2的距离也必须相等，那么点C应选在何处？请在图中，用尺规作图找出所有符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）‎ 考点：‎ 作图—应用与设计作图．‎ 分析：‎ 仔细分析题意，寻求问题的解决方案．‎ 到城镇A、B距离相等的点在线段AB的垂直平分线上，到两条公路距离相等的点在两条公路所夹角的角平分线上，分别作出垂直平分线与角平分线，它们的交点即为所求作的点C．‎ 由于两条公路所夹角的角平分线有两条，因此点C有2个．‎ 解答：‎ 解：（1）作出线段AB的垂直平分线；‎ ‎（2）作出角的平分线（2条）；‎ 它们的交点即为所求作的点C（2个）．‎ 点评：‎ 本题借助实际场景，考查了几何基本作图的能力，考查了线段垂直平分线和角平分线的性质及应用．题中符合条件的点C有2个，注意避免漏解．‎ ‎　‎ ‎22．（8分）（2013•白银）某市在地铁施工期间，交管部门在施工路段设立了矩形路况警示牌BCEF（如图所示），已知立杆AB的高度是3米，从侧面D点测到路况警示牌顶端C点和底端B点的仰角分别是60°和45°，求路况警示牌宽BC的值．‎ 考点：‎ 解直角三角形的应用-仰角俯角问题．‎ 专题：‎ 应用题．‎ 分析：‎ 在Rt△ABD中，知道了已知角的对边，可用正切函数求出邻边AD的长；同理在Rt△ABC中，知道了已知角的邻边，用正切值即可求出对边AC的长；进而由BC=AC﹣AB得解．‎ 解答：‎ 解：∵在Rt△ADB中，∠BDA=45°，AB=3米，‎ ‎∴DA=3米，‎ 在Rt△ADC中，∠CDA=60°，‎ ‎∴tan60°=，‎ ‎∴CA=3． ‎ ‎∴BC=CA﹣BA=（3﹣3）米．‎ 答：路况显示牌BC是（3﹣3）米．‎ 点评：‎ 此题主要考查了解直角三角形的应用，当两个直角三角形有公共边时，先求出这条公共边的长是解答此类题的一般思路．‎ ‎　‎ ‎23．（10分）（2013•白银）如图，一次函数与反比例函数的图象相交于点A，且点A的纵坐标为1．‎ ‎（1）求反比例函数的解析式；‎ ‎（2）根据图象写出当x＞0时，一次函数的值大于反比例函数的值的x的取值范围．‎ 考点：‎ 反比例函数与一次函数的交点问题．‎ 分析：‎ ‎（1）一次函数是完整的函数，把点A的纵坐标代入即可求得M的坐标；然后把A的坐标代入反比例函数解析式，即可求得反比例函数的解析式；‎ ‎（2）根据交点A的坐标，即可得到当x＞0时，一次函数的值大于反比例函数的值的x的取值范围．‎ 解答：‎ 解：（1）点A在y=x﹣2上，‎ ‎∴1=x﹣2，‎ 解得x=6，‎ 把（6，1）代入得 m=6×1=6．‎ ‎∴y=；‎ ‎（2）由图象得，当x＞6时，一次函数的值大于反比例函数的值．‎ 点评：‎ 本题考查用待定系数法求函数解析式；注意：无论是求自变量的取值范围还是函数值的取值范围，都应该从交点入手思考；同时要注意反比例函数的自变量不能取0．‎ ‎　‎ 四、解答题（二）：本大题共5小题，共50分，解答时，应写出必要的文字说明、证明过程或演算步骤。‎ ‎24．（8分）（2013•白银）为了决定谁将获得仅有的一张科普报告入场劵，甲和乙设计了如下的摸球游戏：在不透明口袋中放入编号分别为1、2、3的三个红球及编号为4的一个白球，四个小球除了颜色和编号不同外，其它没有任何区别，摸球之前将袋内的小球搅匀，甲先摸两次，每次摸出一个球（第一次摸后不放回）把甲摸出的两个球放回口袋后，乙再摸，乙只摸一次且摸出一个球，如果甲摸出的两个球都是红色，甲得1分，否则，甲得0分，如果乙摸出的球是白色，乙得1分，否则乙得0分，得分高的获得入场卷，如果得分相同，游戏重来．‎ ‎（1）运用列表或画树状图求甲得1分的概率；‎ ‎（2）请你用所学的知识说明这个游戏是否公平？‎ 考点：‎ 游戏公平性；列表法与树状图法．‎ 分析：‎ ‎（1）首先根据题意列出表格或画出树状图，然后求得所有等可能的结果与甲得1分的情况，然后利用概率公式求解即可求得答案；‎ ‎（2）由（1）求得乙的得分，比较概率不相等，即可得这个游戏是不公平．‎ 解答：‎ 解：（1）列表得：‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎﹣‎ ‎1分 ‎1分 ‎0分 ‎2‎ ‎1分 ‎﹣‎ ‎1分 ‎0分 ‎3‎ ‎1分 ‎1分 ‎﹣‎ ‎0分 ‎4‎ ‎0分 ‎0分 ‎0分 ‎﹣‎ 画树状图得：‎ ‎∴P（甲得1分）==‎ ‎（2）不公平．‎ ‎∵P（乙得1分）=‎ ‎∴P（甲得1分）≠P（乙得1分），‎ ‎∴不公平．‎ 点评：‎ 本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．‎ ‎　‎ ‎25．（10分）（2012•乐山）在读书月活动中，学校准备购买一批课外读物．为使课外读物满足同学们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图．‎ 请你根据统计图提供的信息，解答下列问题：‎ ‎（1）本次调查中，一共调查了　200　名同学；‎ ‎（2）条形统计图中，m=　40　，n=　60　；‎ ‎（3）扇形统计图中，艺术类读物所在扇形的圆心角是　72　度；‎ ‎（4）学校计划购买课外读物6000册，请根据样本数据，估计学校购买其他类读物多少册比较合理？‎ 考点：‎ 条形统计图；用样本估计总体；扇形统计图．‎ 分析：‎ ‎（1）结合两个统计图，根据条形图得出文学类人数为：70，利用扇形图得出文学类所占百分比为：35%，即可得出总人数；‎ ‎（2）利用科普类所占百分比为：30%，则科普类人数为：n=200×30%=60人，即可得出m的值；‎ ‎（3）根据艺术类读物所在扇形的圆心角是：×360°=72°；‎ ‎（3）根据喜欢其他类读物人数所占的百分比，即可估计6000册中其他读物的数量；‎ 解答：‎ 解：（1）根据条形图得出文学类人数为：70，利用扇形图得出文学类所占百分比为：35%，‎ 故本次调查中，一共调查了：70÷35%=200人，‎ 故答案为：200； ‎ ‎（2）根据科普类所占百分比为：30%，‎ 则科普类人数为：n=200×30%=60人，‎ m=200﹣70﹣30﹣60=40人，‎ 故m=40，n=60； ‎ 故答案为：40，60；‎ ‎（3）艺术类读物所在扇形的圆心角是：×360°=72°，‎ 故答案为：72； ‎ ‎（4）由题意，得 （册）．‎ 答：学校购买其他类读物900册比较合理．‎ 点评：‎ 此题主要考查了条形图表和扇形统计图综合应用，将条形图与扇形图结合得出正确信息求出调查的总人数是解题关键．‎ ‎　‎ ‎26．（10分）（2013•白银）如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．‎ ‎（1）BD与CD有什么数量关系，并说明理由；‎ ‎（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．‎ 考点：‎ 矩形的判定；全等三角形的判定与性质．‎ 专题：‎ 证明题．‎ 分析：‎ ‎（1）根据两直线平行，内错角相等求出∠AFE=∠DCE，然后利用“角角边”证明△AEF和△DEC全等，根据全等三角形对应边相等可得AF=CD，再利用等量代换即可得证；‎ ‎（2）先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形，再根据一个角是直角的平行四边形是矩形，可知∠ADB=90°，由等腰三角形三线合一的性质可知必须是AB=AC．‎ 解答：‎ 解：（1）BD=CD．‎ 理由如下：∵AF∥BC，‎ ‎∴∠AFE=∠DCE，‎ ‎∵E是AD的中点，‎ ‎∴AE=DE，‎ 在△AEF和△DEC中，，‎ ‎∴△AEF≌△DEC（AAS），‎ ‎∴AF=CD，‎ ‎∵AF=BD，‎ ‎∴BD=CD；‎ ‎（2）当△ABC满足：AB=AC时，四边形AFBD是矩形．‎ 理由如下：∵AF∥BD，AF=BD，‎ ‎∴四边形AFBD是平行四边形，‎ ‎∵AB=AC，BD=CD，‎ ‎∴∠ADB=90°，‎ ‎∴▱AFBD是矩形．‎ 点评：‎ 本题考查了矩形的判定，全等三角形的判定与性质，平行四边形的判定，是基础题，明确有一个角是直角的平行四边形是矩形是解本题的关键．‎ ‎　‎ ‎27．（10分）（2013•白银）如图，在⊙O中，半径OC垂直于弦AB，垂足为点E．‎ ‎（1）若OC=5，AB=8，求tan∠BAC；‎ ‎（2）若∠DAC=∠BAC，且点D在⊙O的外部，判断直线AD与⊙O的位置关系，并加以证明．‎ 考点：‎ 切线的判定；勾股定理；垂径定理．‎ 专题：‎ 计算题．‎ 分析：‎ ‎（1）根据垂径定理由半径OC垂直于弦AB，AE=AB=4，再根据勾股定理计算出OE=3，则EC=2，然后在Rt△AEC中根据正切的定义可得到tan∠BAC的值；‎ ‎（2）根据垂径定理得到AC弧=BC弧，再利用圆周角定理可得到∠AOC=2∠BAC，由于∠DAC=∠BAC，所以∠AOC=∠BAD，利用∠AOC+∠OAE=90°即可得到∠BAD+∠OAE=90°，然后根据切线的判定方法得AD为⊙O的切线．‎ 解答：‎ 解：（1）∵半径OC垂直于弦AB，‎ ‎∴AE=BE=AB=4，‎ 在Rt△OAE中，OA=5，AE=4，‎ ‎∴OE==3，‎ ‎∴EC=OC﹣OE=5﹣3=2，‎ 在Rt△AEC中，AE=4，EC=2，‎ ‎∴tan∠BAC===；‎ ‎（2）AD与⊙O相切．理由如下：‎ ‎∵半径OC垂直于弦AB，‎ ‎∵AC弧=BC弧，‎ ‎∴∠AOC=2∠BAC，‎ ‎∵∠DAC=∠BAC，‎ ‎∴∠AOC=∠BAD，‎ ‎∵∠AOC+∠OAE=90°，‎ ‎∴∠BAD+∠OAE=90°，‎ ‎∴OA⊥AD，‎ ‎∴AD为⊙O的切线．‎ 点评：‎ 本题考查了切线的判定定理：过半径的外端点且与半径垂直的直线为圆的切线．也考查了勾股定理以及垂径定理、圆周角定理．‎ ‎　‎ ‎28．（12分）（2013•白银）如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；‎ ‎（3）对于（2）中的点B，在此抛物线上是否存在点P，使∠POB=90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由．‎ 考点：‎ 二次函数综合题．‎ 分析：‎ ‎（1）将原点坐标代入抛物线中即可求出k的值，也就得出了抛物线的解析式．‎ ‎（2）根据（1）得出的抛物线的解析式可得出A点的坐标，也就求出了OA的长，根据△OAB的面积可求出B点纵坐标的绝对值，然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标，然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可．‎ ‎（3）根据B点坐标可求出直线OB的解析式，由于OB⊥OP，由此可求出P点的坐标特点，代入二次函数解析式可得出P点的坐标．求△POB的面积时，可先求出OB，OP的长度即可求出△BOP的面积．‎ 解答：‎ 解：①∵函数的图象与x轴相交于O，‎ ‎∴0=k+1，‎ ‎∴k=﹣1，‎ ‎∴y=x2﹣3x，‎ ‎②假设存在点B，过点B做BD⊥x轴于点D，‎ ‎∵△AOB的面积等于6，‎ ‎∴AO•BD=6，‎ 当0=x2﹣3x，‎ x（x﹣3）=0，‎ 解得：x=0或3，‎ ‎∴AO=3，‎ ‎∴BD=4‎ ‎ 即4=x2﹣3x，‎ ‎ 解得：x=4或x=﹣1（舍去）．‎ 又∵顶点坐标为：（ 1.5，﹣2.25）．‎ ‎∵2.25＜4，‎ ‎∴x轴下方不存在B点，‎ ‎∴点B的坐标为：（4，4）；‎ ‎③∵点B的坐标为：（4，4），‎ ‎∴∠BOD=45°，BO==4，‎ 当∠POB=90°，‎ ‎∴∠POD=45°，‎ 设P点横坐标为：﹣x，则纵坐标为：x2﹣3x，‎ 即﹣x=x2﹣3x，‎ 解得x=2 或x=0，‎ ‎∴在抛物线上仅存在一点P （2，﹣2）．‎ ‎∴OP==2，‎ 使∠POB=90°，‎ ‎∴△POB的面积为： PO•BO=×4×2=8．‎ 点评：‎ 本题考查了二次函数解析式的确定、函数图象交点、图象面积求法等知识．利用已知进行分类讨论得出符合要求点的坐标是解题关键．‎ ‎　‎