2014年湖北省宜昌市中考数学试题（含答案） 17页

‎2014年湖北省宜昌市中考数学试卷 参考答案与试题解析 ‎　‎ 一、单项选择题（共15小题，每小题3分，满分45分）‎ ‎1．（3分）（2014•宜昌）三峡大坝全长约2309米，这个数据用科学记数法表示为（　　）米．‎ ‎　‎ A．‎ ‎2.309×103‎ B．‎ ‎23.09×102‎ C．‎ ‎0.2309×104‎ D．‎ ‎2.309×10﹣3‎ 考点：‎ 科学记数法—表示较大的数．菁优网版权所有 分析：‎ 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ 解答：‎ 解：2309=2.309×103，‎ 故选：A．‎ 点评：‎ 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎2．（3分）（2014•宜昌）在﹣2，0，3，这四个数中，最大的数是（　　）‎ ‎　‎ A．‎ ‎﹣2‎ B．‎ ‎0‎ C．‎ ‎3‎ D．‎ 考点：‎ 实数大小比较．菁优网版权所有 分析：‎ 根据正数大于0，0大于负数，可得答案．‎ 解答：‎ 解：﹣2＜0＜＜3，‎ 故选：C．‎ 点评：‎ 本题考查了实数比较大小，是解题关键．‎ ‎　‎ ‎3．（3分）（2014•宜昌）平行四边形的内角和为（　　）‎ ‎　‎ A．‎ ‎180°‎ B．‎ ‎270°‎ C．‎ ‎360°‎ D．‎ ‎640°‎ 考点：‎ 多边形内角与外角．菁优网版权所有 分析：‎ 利用多边形的内角和=（n﹣2）•180°即可解决问题 解答：‎ 解：解：根据多边形的内角和可得：‎ ‎（4﹣2）×180°=360°．‎ 故选：C．‎ 点评：‎ 本题考查了对于多边形内角和定理的识记．n边形的内角和为（n﹣2）•180°．‎ ‎　‎ ‎4．（3分）（2014•宜昌）作业时间是中小学教育质量综合评价指标的考查要点之一，腾飞学习小组五个同学每天课外作业时间分别是（单位：分钟）：60，80，75，45，120．这组数据的中位数是（　　）‎ ‎　‎ A．‎ ‎45‎ B．‎ ‎75‎ C．‎ ‎80‎ D．‎ ‎60‎ 考点：‎ 中位数．菁优网版权所有 分析：‎ 根据中位数的概念求解即可．‎ 解答：‎ 解：将数据从小到大排列为：45，60，75，80，120，‎ 中位数为75．‎ 故选B．‎ 点评：‎ 本题考查了中位数的定义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．‎ ‎　‎ ‎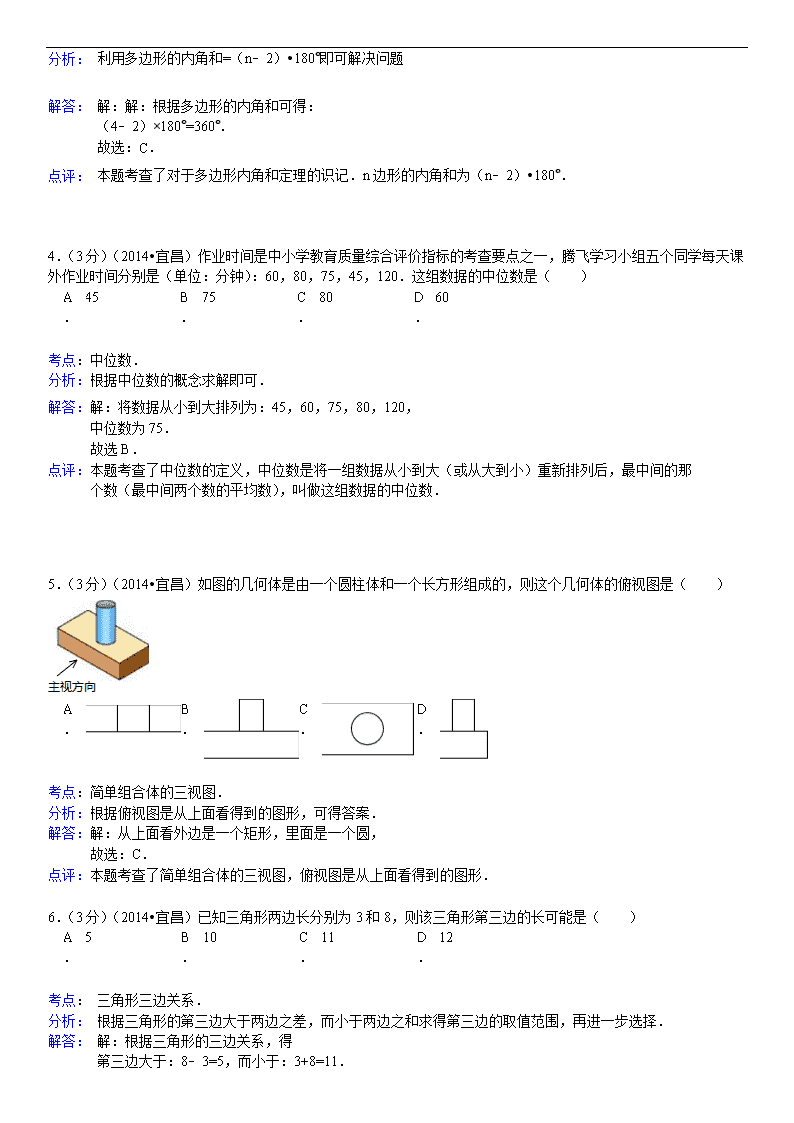5．（3分）（2014•宜昌）如图的几何体是由一个圆柱体和一个长方形组成的，则这个几何体的俯视图是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 简单组合体的三视图．菁优网版权所有 分析：‎ 根据俯视图是从上面看得到的图形，可得答案．‎ 解答：‎ 解：从上面看外边是一个矩形，里面是一个圆，‎ 故选：C．‎ 点评：‎ 本题考查了简单组合体的三视图，俯视图是从上面看得到的图形．‎ ‎　‎ ‎6．（3分）（2014•宜昌）已知三角形两边长分别为3和8，则该三角形第三边的长可能是（　　）‎ ‎　‎ A．‎ ‎5‎ B．‎ ‎10‎ C．‎ ‎11‎ D．‎ ‎12‎ 考点：‎ 三角形三边关系．菁优网版权所有 分析：‎ 根据三角形的第三边大于两边之差，而小于两边之和求得第三边的取值范围，再进一步选择．‎ 解答：‎ 解：根据三角形的三边关系，得 第三边大于：8﹣3=5，而小于：3+8=11．‎ 则此三角形的第三边可能是：10．‎ 故选：B．‎ 点评：‎ 本题考查了三角形的三边关系，即三角形的第三边大于两边之差，而小于两边之和，此题基础题，比较简单．‎ ‎7．（3分）（2014•宜昌）下列计算正确的是（　　）‎ ‎　‎ A．‎ a+2a2=3a3‎ B．‎ a3•a2=a6‎ C．‎ a6+a2=a3‎ D．‎ ‎（ab）3=a3b3‎ 考点：‎ 幂的乘方与积的乘方；合并同类项；同底数幂的乘法．菁优网版权所有 分析：‎ 根据合并同类项法则，同底数幂的乘法，积的乘方分别求出每个式子的结果，再判断即可．‎ 解答：‎ 解：A、a和2a2不能合并，故本选项错误；‎ B、a3•a2=a5，故本选项错误；‎ C、a6和a2不能合并，故本选项错误；‎ D、（ab）3=a3b3，故本选项正确；‎ 故选D．[来源:Zxxk.Com]‎ 点评：‎ 本题考查了合并同类项法则，同底数幂的乘法，积的乘方的应用，主要考查学生的计算能力．‎ ‎　‎ ‎8．（3分）（2014•宜昌）2014年3月，YC市举办了首届中学生汉字听写大会，从甲、乙、丙、丁4套题中随机抽取一套训练，抽中甲的概率是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎1‎ 考点：‎ 概率公式．菁优网版权所有 分析：‎ 四套题中抽一套进行训练，利用概率公式直接计算即可．‎ 解答：‎ 解：∵从甲、乙、丙、丁4套题中随机抽取一套训练，‎ ‎∴抽中甲的概率是，‎ 故选C．‎ 点评：‎ 本题考查了概率的公式，能记住概率的求法是解决本题的关键，比较简单．‎ ‎　‎ ‎9．（3分）（2014•宜昌）如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（　　）[来源:学科网]‎ ‎　‎ A．‎ AB=24m B．‎ MN∥AB C．‎ ‎△CMN∽△CAB D．‎ CM：MA=1：2‎ 考点：‎ 三角形中位线定理；相似三角形的应用．菁优网版权所有 专题：‎ 应用题．‎ 分析：‎ 根据三角形的中位线平行于第三边并且等于第三边的一半可得MN∥AB，MN=AB，再根据相似三角形的判定解答．‎ 解答：‎ 解：∵M、N分别是AC，BC的中点，‎ ‎∴MN∥AB，MN=AB，‎ ‎∴AB=2MN=2×12=24m，‎ ‎△CMN∽△CAB，‎ ‎∵M是AC的中点，‎ ‎∴CM=MA，‎ ‎∴CM：MA=1：1，‎ 故描述错误的是D选项．‎ 故选D．‎ 点评：‎ 本题考查了三角形的中位线平行于第三边并且等于第三边的一半，相似三角形的判定，熟记定理并准确识图是解题的关键．‎ ‎　‎ ‎10．（3分）（2014•宜昌）如图，在△ABC中，AB=AC，∠A=30°，以B为圆心，BC的长为半径圆弧，交AC于点D，连接BD，则∠ABD=（　　）‎ ‎　‎ A．‎ ‎30‎ B．‎ ‎45‎ C．‎ ‎60‎ D．‎ ‎90‎ 考点：‎ 等腰三角形的性质．菁优网版权所有 分析：‎ 根据等腰三角形两底角相等求出∠ABC=∠ACB，再求出∠CBD，然后根据∠ABD=∠ABC﹣∠CBD计算即可得解．‎ 解答：‎ 解：∵AB=AC，∠A=30°，‎ ‎∴∠ABC=∠ACB=（180°﹣∠A）=（180°﹣30°）=75°，‎ ‎∵以B为圆心，BC的长为半径圆弧，交AC于点D，‎ ‎∴BC=BD，‎ ‎∴∠CBD=180°﹣2∠ACB=180°﹣2×75°=30°，‎ ‎∴∠ABD=∠ABC﹣∠CBD=75°﹣30°=45°．‎ 故选B．‎ 点评：‎ 本题考查了等腰三角形的性质，主要利用了等腰三角形两底角相等，熟记性质是解题的关键．‎ ‎　‎ ‎11．（3分）（2014•宜昌）要使分式有意义，则的取值范围是（　　）‎ ‎　‎ A．‎ x≠1‎ B．‎ x＞1‎ C．‎ x＜1‎ D．‎ x≠﹣1‎ 考点：‎ 分式有意义的条件．菁优网版权所有 分析：‎ 根据分母不等于0列式计算即可得解．‎ 解答：‎ 解：由题意得，x﹣1≠0，‎ 解得x≠1．‎ 故选A．‎ 点评：‎ 本题考查了分式有意义的条件，从以下三个方面透彻理解分式的概念：‎ ‎（1）分式无意义⇔分母为零；‎ ‎（2）分式有意义⇔分母不为零；‎ ‎（3）分式值为零⇔分子为零且分母不为零．‎ ‎　‎ ‎12．（3分）（2014•宜昌）如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则∠ABD=（　　）‎ ‎　‎ A．‎ ‎∠ACD B．‎ ‎∠ADB C．‎ ‎∠AED D．‎ ‎∠ACB 考点：‎ 圆周角定理．菁优网版权所有 分析：‎ 根据圆周角定理即可判断A、B、D，根据三角形外角性质即可判断C．‎ 解答：‎ 解：A、∵∠ABD对的弧是弧AD，∠ACD对的弧也是AD，‎ ‎∴∠ABD=∠ACD，故本选项正确；‎ B、∵∠ABD对的弧是弧AD，∠ADB对的弧也是AB，而已知没有说弧AD=弧AB，‎ ‎∴∠ABD和∠ACD不相等，故本选项错误；‎ C、∠AED＞∠ABD，故本选项错误；‎ D、∵∠ABD对的弧是弧AD，∠ACB对的弧也是AB，而已知没有说弧AD=弧AB，‎ ‎∴∠ABD和∠ACB不相等，故本选项错误；‎ 故选A．‎ 点评：‎ 本题考查了圆周角定理和三角形外角性质的应用，注意：在同圆或等哦圆中，同弧或等弧所对的圆周角相等．‎ ‎　‎ ‎13．（3分）（2014•宜昌）如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则的长为（　　）‎ ‎　‎ A．‎ π B．‎ ‎6π C．‎ ‎3π D．‎ ‎1.5π 考点：‎ 旋转的性质；弧长的计算．菁优网版权所有 分析：‎ 根据弧长公式列式计算即可得解．‎ 解答：‎ 解：的长==1.5π．‎ 故选D．‎ 点评：‎ 本题考查了旋转的性质，弧长的计算，熟记弧长公式是解题的关键．‎ ‎　‎ ‎14．（3分）（2014•宜昌）如图，M，N两点在数轴上表示的数分别是m，n，则下列式子中成立的是（　　）‎ ‎　‎ A．‎ m+n＜0‎ B．‎ ‎﹣m＜﹣n C．‎ ‎|m|﹣|n|＞0‎ D．‎ ‎2+m＜2+n 考点：‎ 实数与数轴．菁优网版权所有 分析：‎ 根据M、N两点在数轴上的位置判断出其取值范围，再对各选项进行逐一分析即可．‎ 解答：‎ 解：M、N两点在数轴上的位置可知：﹣1＜M＜0，N＞2，‎ ‎∵M+N＞O，故A错误，‎ ‎∵﹣M＞﹣N，故B错误，‎ ‎∵|m|﹣|n|＜，0故C错误．‎ ‎∵2+m＜2+n正确，‎ ‎∴D选项正确．‎ 故选：D．‎ 点评：‎ 本题考查的是数轴的特点，根据a、b两点在数轴上的位置判断出其取值范围是解答此题的关键．‎ ‎　‎ ‎15．（3分）（2014•宜昌）二次函数y=ax2+b（b＞0）与反比例函数y=在同一坐标系中的图象可能是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 二次函数的图象；反比例函数的图象．菁优网版权所有 专题：‎ 数形结合．‎ 分析：‎ 先根据各选项中反比例函数图象的位置确定a的范围，再根据a的范围对抛物线的大致位置进行判断，从而确定该选项是否正确．‎ 解答：‎ 解：A、对于反比例函数y=经过第二、四象限，则a＜0，所以抛物线开口向下，所以A选项错误；‎ B、对于反比例函数y=经过第一、三象限，则a＞0，所以抛物线开口向上，b＞0，抛物线与y轴的交点在x轴上方，所以B选项正确；‎ C、对于反比例函数y=经过第一、三象限，则a＞0，所以抛物线开口向上，所以C选项正确；‎ D、对于反比例函数y=经过第一、三象限，则a＞0，所以抛物线开口向上，而b＞0，抛物线与y轴的交点在x轴上方，所以D选项错误．‎ 故选B．‎ 点评：‎ 本题考查了二次函数的图象：二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象为抛物线，当a＞0，抛物线开口向上；当a＜0，抛物线开口向下．对称轴为直线x=﹣；与y轴的交点坐标为（0，c）．也考查了反比例函数的图象．‎ ‎　‎ 二、解答题（共9小题，共75分）‎ ‎16．（6分）（2014•宜昌）计算：+|﹣2|+（﹣6）×（﹣）．‎ 考点：‎ 实数的运算．菁优网版权所有 分析：‎ 本题涉及绝对值、二次根式化简、有理数的乘法三个考点．针对每个考点分别进行计算，然后再计算有理数的加法即可．‎ 解答：‎ 解：原式=2+2+4=8．‎ 点评：‎ 本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握二次根式、绝对值等考点的运算．‎ ‎　‎ ‎17．（6分）（2014•宜昌）化简：（a+b）（a﹣b）+2b2．‎ 考点：‎ 平方差公式；合并同类项．菁优网版权所有 分析：‎ 先根据平方差公式算乘法，再合并同类项即可．‎ 解答：‎ 解：原式=a2﹣b2+2b2‎ ‎=a2+b2．‎ 点评：‎ 本题考查了平方差公式和整式的混合运算的应用，主要考查学生的化简能力．‎ ‎　‎ ‎18．（7分）（2014•宜昌）如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．‎ ‎（1）求∠CAD的度数；‎ ‎（2）延长AC至E，使CE=AC，求证：DA=DE．‎ 考点：‎ 全等三角形的判定与性质．菁优网版权所有 分析：‎ ‎（1）利用“直角三角形的两个锐角互余”的性质和角平分的性质进行解答；‎ ‎（2）通过证△ACD≌△ECD来推知DA=DE．‎ 解答：‎ ‎（1）解：如图，∵在Rt△ABC中，∠ACB=90°，∠B=30°，‎ ‎∴∠B=30°，‎ ‎∴∠CAB=60°．‎ 又∵AD平分∠CAB，‎ ‎∴∠CAD=∠CAB=30°，即∠CAD=30°；‎ ‎（2）证明：∵∠ACD+∠ECD=180°，且∠ACD=90°，‎ ‎∴∠ECD=90°，‎ ‎∴∠ACD=∠ECD．‎ 在△ACD与△ECD中，，‎ ‎∴△ACD≌△ECD（SAS），‎ ‎∴DA=DE．‎ 点评：‎ 本题考查了全等三角形的判定与性质．在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．‎ ‎　‎ ‎19．（7分）（2014•宜昌）下表中，y是x的一次函数． ‎ ‎ x ‎﹣2‎ ‎ 1‎ ‎ 2‎ ‎　4　‎ ‎ 5‎ ‎ y ‎ 6‎ ‎﹣3‎ ‎　﹣6　‎ ‎﹣12‎ ‎﹣15‎ ‎（1）求该函数的表达式，并补全表格；‎ ‎（2）已知该函数图象上一点M（1，﹣3）也在反比例函数y=图象上，求这两个函数图象的另一交点N的坐标．‎ 考点：‎ 反比例函数与一次函数的交点问题；待定系数法求一次函数解析式．菁优网版权所有 分析：‎ ‎（1）设y=kx+b，将点（﹣2，6）、（5，﹣15）代入可得函数解析式，也可补全表格；‎ ‎（2）将点M的坐标代入，可得m的值，联立一次函数及反比例函数解析式可得另一交点坐标．‎ 解答：‎ 解：（1）设该一次函数为y=kx+b（k≠0），‎ ‎∵当x=﹣2时，y=6，当x=1时，y=﹣3，‎ ‎∴，‎ 解得：，‎ ‎∴一次函数的表达式为：y=﹣3x，‎ 当x=2时，y=﹣6；当y=﹣12时，x=4．‎ 补全表格如题中所示．‎ ‎（2）∵点M（1，﹣3）在反比例函数y=上（m≠0），‎ ‎∴﹣3=，‎ ‎∴m=﹣3，‎ ‎∴反比例函数解析式为：y=﹣，‎ 联立可得，‎ 解得：或，‎ ‎∴另一交点坐标为（﹣1，3）．‎ 点评：‎ 本题考查了反比例函数与一次函数的交点问题，解答本题的关键是熟练待定系数法的运用，难度一般．‎ ‎　‎ ‎20．（8分）（2014•宜昌）“低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门抽样调查了某单位员工上下班的交通方式，绘制了如下统计图：‎ ‎（1）填空：样本中的总人数为　80　；开私家车的人数m=　20　；扇形统计图中“骑自行车”所在扇形的圆心角为　72　度；‎ ‎（2）补全条形统计图；‎ ‎（3）该单位共有2000人，积极践行这种生活方式，越来越多的人上下班由开私家车改为骑自行车．若步行，坐公交车上下班的人数保持不变，问原来开私家车的人中至少有多少人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数？‎ ‎[来源:学§科§网Z§X§X§K]‎ 考点：‎ 条形统计图；一元一次不等式的应用；扇形统计图．菁优网版权所有 专题：‎ 图表型．‎ 分析：‎ ‎（1）用乘公交车的人数除以所占的百分比，计算即可求出总人数，再用总人数乘以开私家车的所占的百分比求出m，用360°乘以骑自行车的所占的百分比计算即可得解；‎ ‎（2）求出骑自行车的人数，然后补全统计图即可；‎ ‎（3）设原来开私家车的人中有x人改为骑自行车，表示出改后骑自行车的人数和开私家车的人数，列式不等式，求解即可．‎ 解答：‎ 解：（1）样本中的总人数为：36÷45%=80人，‎ 开私家车的人数m=80×25%=20；‎ 扇形统计图中“骑自行车”所占的百分比为：1﹣10%﹣25%﹣45%=20%，‎ 所在扇形的圆心角为360°×20%=72°；‎ 故答案为：80，20，72；‎ ‎（2）骑自行车的人数为：80×20%=16人，‎ 补全统计图如图所示；‎ ‎（3）设原来开私家车的人中有x人改为骑自行车，‎ 由题意得，×2000+x≥×2000﹣x，‎ 解得x≥50，‎ 答：原来开私家车的人中至少有50人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数．‎ 点评：‎ 本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．‎ ‎　‎ ‎21．（8分）（2014•宜昌）已知：如图，四边形ABCD为平行四边形，以CD为直径作⊙O，⊙O与边BC相交于点F，⊙O的切线DE与边AB相交于点E，且AE=3EB．‎ ‎（1）求证：△ADE∽△CDF；‎ ‎（2）当CF：FB=1：2时，求⊙O与▱ABCD的面积之比．‎ 考点：‎ 切线的性质；勾股定理；平行四边形的性质；相似三角形的判定与性质．菁优网版权所有 分析：‎ ‎（1）根据平行四边形的性质得出∠A=∠C，AD∥BC，求出∠ADE=∠CDF，根据相似三角形的判定推出即可；‎ ‎（2）设CF=x，FB=2x，则BC=3x，设EB=y，则AE=3y，AB=4y，根据相似得出=，求出x=2y，由勾股定理得求出DF=2y，分别求出⊙O的面积和四边形ABCD的面积，即可求出答案．‎ 解答：‎ ‎（1）证明：∵CD是⊙O的直径，‎ ‎∴∠DFC=90°，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴∠A=∠C，AD∥BC，‎ ‎∴∠ADF=∠DFC=90°，‎ ‎∵DE为⊙O的切线，‎ ‎∴DE⊥DC，‎ ‎∴∠EDC=90°，‎ ‎∴∠ADF=∠EDC=90°，‎ ‎∴∠ADE=∠CDF，‎ ‎∵∠A=∠C，‎ ‎∴△ADE∽△CDE；‎ ‎（2）解：∵CF：FB=1：2，‎ ‎∴设CF=x，FB=2x，则BC=3x，‎ ‎∵AE=3EB，‎ ‎∴设EB=y，则AE=3y，AB=4y，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD=BC=3x，AB=DC=4y，‎ ‎∵△ADE∽△CDF，‎ ‎∴=，‎ ‎∴=，[来源:学科网]‎ ‎∵x、y均为正数，‎ ‎∴x=2y，‎ ‎∴BC=6y，CF=2y，‎ 在Rt△DFC中，∠DFC=90°，‎ 由勾股定理得：DF===2y，‎ ‎∴⊙O的面积为π•（DC）2=π•DC2=π（4y）2=4πy2，‎ 四边形ABCD的面积为BC•DF=6y•2y=12y2，‎ ‎∴⊙O与四边形ABCD的面积之比为4πy2：12y2=π：3．‎ 点评：‎ 本题考查了平行四边形的性质，相似三角形的性质和判定，勾股定理的应用，主要考查学生综合运用性质进行推理和计算的能力．‎ ‎　‎ ‎22．（10分）（2014•宜昌）在“文化宜昌•全民阅读”活动中，某中学社团“精一读书社”对全校学生的人数及纸质图书阅读量（单位：本）进行了调查，2012年全校有1000名学生，2013年全校学生人数比2012年增加10%，2014年全校学生人数比2013年增加100人．‎ ‎（1）求2014年全校学生人数；‎ ‎（2）2013年全校学生人均阅读量比2012年多1本，阅读总量比2012年增加1700本（注：阅读总量=人均阅读量×人数）‎ ‎①求2012年全校学生人均阅读量；‎ ‎②2012年读书社人均阅读量是全校学生人均阅读量的2.5倍，如果2012年、2014年这两年读书社人均阅读量都比前一年增长一个相同的百分数a，2014年全校学生人均阅读量比2012年增加的百分数也是a，那么2014年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%，求a的值．‎ 考点：‎ 一元二次方程的应用；一元一次方程的应用．菁优网版权所有 分析：‎ ‎（1）根据题意，先求出2013年全校的学生人数就可以求出2014年的学生人数；‎ ‎（2）①设2012人均阅读量为x本，则2013年的人均阅读量为（x+1）本，根据阅读总量之间的数量关系建立方程就可以得出结论；‎ ‎②由①的结论就可以求出2012年读书社的人均读书量，2014年读书社的人均读书量，全校的人均读书量，由2014年读书社的读书量与全校读书量之间的关系建立方程求出其解即可．‎ 解答：‎ 解：（1）由题意，得 ‎2013年全校学生人数为：1000×（1+10%）=1100人，‎ ‎∴2014年全校学生人数为：1100+100=1200人；‎ ‎（2）①设2012人均阅读量为x本，则2013年的人均阅读量为（x+1）本，由题意，得 ‎1100（x+1）=1000x+1700，‎ 解得：x=6．‎ 答：2012年全校学生人均阅读量为6本；‎ ‎②由题意，得 ‎2012年读书社的人均读书量为：2.5×6=15本，‎ ‎2014年读书社人均读书量为15（1+a）2本，‎ ‎2014年全校学生的读书量为6（1+a）本，‎ ‎80×15（1+a）2=1200×6（1+a）×25%‎ ‎2（1+a）2=3（1+a），‎ ‎∴a1=﹣1（舍去），a2=0.5．‎ 答：a的值为0.5．‎ 点评：‎ 本题考查了列一元一次方程解实际问题的运用，一元二次方程的解法的运用，增长率问题的数量关系的运用，解答时根据阅读总量之间的关系建立方程是关键．‎ ‎　‎ ‎23．（11分）（2014•宜昌）在矩形ABCD中，=a，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．‎ ‎（1）如图1，当DH=DA时，‎ ‎①填空：∠HGA=　45　度；‎ ‎②若EF∥HG，求∠AHE的度数，并求此时的最小值；‎ ‎（2）如图3，∠AEH=60°，EG=2BG，连接FG，交边FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．‎ 考点：‎ 四边形综合题．菁优网版权所有 分析：‎ ‎（1）①根据矩形的性质和已知条件得出∠HAE=45°，再根据HA=HG，得出∠HAE=∠HGA，从而得出答案；‎ ‎②先分两种情况讨论：第一种情况，根据（1）得出∠AHG=90°，再根据折叠的性质得出∠HAE=∠F=45°，∠AHE=∠FHE，再根据EF∥HG，得出∠AHF=∠AHG﹣∠FHG，即可得出∠AHE=22.5°，此时，当B与G重合时，a的值最小，求出最小值；第二种情况：根据已知得出∠AEH+∠FEH=45°，由折叠的性质求出∠AHE的度数，此时，当B与E重合时，a的值最小，设DH=DA=x，则AH=CH=x，在Rt△AHG中，∠AHG=90°，根据勾股定理得：AG=AH=2x，再根据∠AEH=∠FEH，∠GHE=∠FEH，求出∠AEH=∠GHE，得出AB=AE=2x+x，从而求出a的最小值；‎ ‎（2）先过点H作HQ⊥AB于Q，则∠AQH=∠GOH=90°，根据矩形的性质得出∠D=∠DAQ=∠AQH=90°，得出四边形DAQH为矩形，设AD=x，GB=y，则HQ=x，EG=2y，‎ 由折叠的性质可知∠AEH=∠FEH=60°，得出∠FEG=60°，在Rt△EFG中，根据特殊角的三角函数值求出EG和EQ的值，再由折叠的性质得出AE=EF，求出y的值，从而求出AB=2AQ+GB，即可得出a的值．‎ 解答：‎ 解：（1）①∵四边形ABCD是矩形，‎ ‎∴∠ADH=90°，‎ ‎∵DH=DA，‎ ‎∴∠DAH=∠DHA=45°，‎ ‎∴∠HAE=45°，‎ ‎∵HA=HG，‎ ‎∴∠HAE=∠HGA=45°；‎ 故答案为：45°；‎ ‎②分两种情况讨论：‎ 第一种情况：‎ ‎∵∠HAG=∠HGA=45°；‎ ‎∴∠AHG=90°，‎ 由折叠可知：∠HAE=∠F=45°，∠AHE=∠FHE，‎ ‎∵EF∥HG，‎ ‎∴∠FHG=∠F=45°，‎ ‎∴∠AHF=∠AHG﹣∠FHG=45°，‎ 即∠AHE+∠FHE=45°，‎ ‎∴∠AHE=22.5°，‎ 此时，当B与G重合时，a的值最小，最小值是2；‎ 第二种情况：‎ ‎∵EF∥HG，‎ ‎∴∠HGA=∠FEA=45°，‎ 即∠AEH+∠FEH=45°，‎ 由折叠可知：∠AEH=∠FEH，‎ ‎∴∠AEH=∠FEH=22.5°，‎ ‎∵EF∥HG，‎ ‎∴∠GHE=∠FEH=22.5°，‎ ‎∴∠AHE=90°+22.5°=112.5°，‎ 此时，当B与E重合时，a的值最小，‎ 设DH=DA=x，则AH=CH=x，‎ 在Rt△AHG中，∠AHG=90°，由勾股定理得：‎ AG=AH=2x，‎ ‎∵∠AEH=∠FEH，∠GHE=∠FEH，[来源:学,科,网Z,X,X,K]‎ ‎∴∠AEH=∠GHE，‎ ‎∴GH=GE=x，‎ ‎∴AB=AE=2x+x，‎ ‎∴a的最小值是=2+；‎ ‎（2）如图：过点H作HQ⊥AB于Q，则∠AQH=∠GOH=90°，‎ 在矩形ABCD中，∠D=∠DAQ=90°，‎ ‎∴∠D=∠DAQ=∠AQH=90°，‎ ‎∴四边形DAQH为矩形，‎ ‎∴AD=HQ，‎ 设AD=x，GB=y，则HQ=x，EG=2y，‎ 由折叠可知：∠AEH=∠FEH=60°，‎ ‎∴∠FEG=60°，‎ 在Rt△EFG中，EG=EF×cos60°，EF=4y，‎ 在Rt△HQE中，EQ==x，‎ ‎∴QG=QE+EG=x+2y，‎ ‎∵HA=HG，HQ⊥AB，‎ ‎∴AQ=GQ=x+2y，‎ ‎∴AE=AQ+QE=x+2y，‎ 由折叠可知：AE=EF，‎ ‎∴x+2y=4y，‎ ‎∴y=x，‎ ‎∴AB=2AQ+GB=2（x+2y）+y=x，‎ ‎∴a==．‎ 点评：‎ 此题考查了四边形的综合，用到的知识点是矩形的性质、折叠的性质、勾股定理、特殊角的三角函数值等知识点，关键是根据题意做出辅助线，构造直角三角形．‎ ‎　‎ ‎24．（12分）（2014•宜昌）如图，在平面直角坐标系中，已知点P（0，4），点A在线段OP上，点B在x轴正半轴上，且AP=OB=t，0＜t＜4，以AB为边在第一象限内作正方形ABCD；过点C、D依次向x轴、y轴作垂线，垂足为M，N，设过O，C两点的抛物线为y=ax2+bx+c．‎ ‎（1）填空：△AOB≌△　DNA或△DPA　≌△BMC（不需证明）；用含t的代数式表示A点纵坐标：A（0，　4﹣t　）；‎ ‎（2）求点C的坐标，并用含a，t的代数式表示b；‎ ‎（3）当t=1时，连接OD，若此时抛物线与线段OD只有唯一的公共点O，求a的取值范围；‎ ‎（4）当抛物线开口向上，对称轴是直线x=2﹣，顶点随着的增大向上移动时，求t的取值范围．‎ 考点：‎ 二次函数综合题．菁优网版权所有 分析：‎ ‎（1）根据全等三角形的判定定理SAS证得：△AOB≌△DNA或DPA≌△BMC；根据图中相关线段间的和差关系来求点A的坐标；‎ ‎（2）利用（1）中的全等三角形的对应边相等易推知：OM=OB+BM=t+4﹣t=4，则C（4，t）．把点O、C的坐标分别代入抛物线y=ax2+bx+c可以求得b=t﹣4a；‎ ‎（3）利用待定系数法求得直线OD的解析式y=x．联立方程组，得，所以ax2+（﹣﹣4a）x=0，解得 x=0或x=4+．‎ 对于抛物线的开口方向进行分类讨论，即a＞0和a＜0两种情况下的a的取值范围；‎ ‎（4）根据抛物线的解析式y=ax2+（﹣4a）x得到顶点坐标是（﹣，﹣（t﹣16a）2）．结合已知条件求得a=t2，故顶点坐标为（2﹣，﹣（t﹣）2）．哟抛物线的性质知：只与顶点坐标有关，故t的取值范围为：0＜t≤．‎ 解答：‎ 解：（1）如图，∵∠DNA=∠AOB=90°，‎ ‎∴∠NAD=∠OBA（同角的余角相等）．‎ 在△AOB与△DNA中，，‎ ‎∴△AOB≌△DNA（SAS）．‎ 同理△DNA≌△BMC．‎ ‎∵点P（0，4），AP=t，‎ ‎∴OA=OP﹣AP=4﹣t．‎ 故答案是：DNA或△DPA；4﹣t；‎ ‎（2）由题意知，NA=OB=t，则OA=4﹣t．‎ ‎∵△AOB≌△BMC，‎ ‎∴CM=OB=t，‎ ‎∴OM=OB+BM=t+4﹣t=4，‎ ‎∴C（4，t）．‎ 又抛物线y=ax2+bx+c过点O、C，‎ ‎∴，‎ 解得 b=t﹣4a；‎ ‎（3）当t=1时，抛物线为y=ax2+（﹣4a）x，NA=OB=1，OA=3．‎ ‎∵△AOB≌△DNA，‎ ‎∴DN=OA=3，‎ ‎∵D（3，4），‎ ‎∴直线OD为：y=x．‎ 联立方程组，得，‎ 消去y，得 ax2+（﹣﹣4a）x=0，‎ 解得 x=0或x=4+，‎ 所以，抛物线与直线OD总有两个交点．‎ 讨论：①当a＞0时，4+＞3，只有交点O，所以a＞0符合题意；‎ ‎②当a＜0时，若4+＞3，则a＜﹣．‎ 又a＜0‎ 所以 a＜﹣．‎ 若4+＜0，则得a＞﹣．‎ 又a＜0，‎ 所以﹣＜a＜0．‎ 综上所述，a的取值范围是a＞0或a＜﹣或﹣＜a＜0．‎ ‎（4）抛物线为y=ax2+（﹣4a）x，则顶点坐标是（﹣，﹣（t﹣16a）2）．‎ 又∵对称轴是直线x=﹣+2=2﹣，‎ ‎∴a=t2，‎ ‎∴顶点坐标为：（2﹣，﹣（1﹣4t）2），即（2﹣，﹣（t﹣）2）．‎ ‎∵抛物线开口向上，且随着t的增大，抛物线的顶点向上移动，‎ ‎∴只与顶点坐标有关，‎ ‎∴t的取值范围为：0＜t≤．‎ 点评：‎ 本题考查了二次函数综合题型．此题难度较大，需要熟练掌握待定系数法求二次函数解析式，全等三角形的判定与性质，二次函数图象的性质等知识点，综合性比较强，需要学生对所学知识进行系统的掌握．‎ ‎　‎