2020年广西北部湾经济区中考数学试卷【含答案；word版本试题；可编辑】1 10页

‎2020年广西北部湾经济区中考数学试卷 一、选择题（共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑．）‎ ‎1. 下列实数是无理数的是（ ）‎ A.‎2‎ B.‎1‎ C.‎0‎ D.‎‎-5‎ ‎2. 下列图形是中心对称图形的是（ ）‎ A. B. C. D.‎ ‎3. ‎2020‎年‎2‎月至‎5‎月，由广西教育厅主办，南宁市教育局承办的广西中小学“空中课堂”是同期全国服务中小学学科最齐、学段最全、上线最早的线上学习课程，深受广大师生欢迎．其中某节数学课的点击观看次数约‎889000‎次，则数据‎889000‎用科学记数法表示为（ ）‎ A.‎88.9×‎‎10‎‎3‎ B.‎88.9×‎‎10‎‎4‎ C.‎8.89×‎‎10‎‎5‎ D.‎‎8.89×‎‎10‎‎6‎ ‎4. 下列运算正确的是（ ）‎ A.‎2x‎2‎+‎x‎2‎＝‎2‎x‎4‎ B.x‎3‎‎⋅‎x‎3‎＝‎2‎x‎3‎ C.‎(‎x‎5‎‎)‎‎2‎＝x‎7‎ D.‎2x‎7‎÷‎x‎5‎＝‎‎2‎x‎2‎ ‎5. 以下调查中，最适合采用全面调查的是（ ）‎ A.检测长征运载火箭的零部件质量情况 B.了解全国中小学生课外阅读情况 C.调查某批次汽车的抗撞击能力 D.检测某城市的空气质量 ‎6. 一元二次方程x‎2‎‎-2x+1‎＝‎0‎的根的情况是（ ）‎ A.有两个不等的实数根 B.有两个相等的实数根 C.无实数根 D.无法确定 ‎7. 如图，在‎△ABC中，BA＝BC，‎∠B＝‎80‎‎∘‎，观察图中尺规作图的痕迹，则‎∠DCE的度数为（ ）‎ A.‎60‎‎∘‎ B.‎65‎‎∘‎ C.‎70‎‎∘‎ D.‎‎75‎‎∘‎ ‎8. 一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在每个岔路口都随机选择一条路径，则它获得食物的概率是（ ）‎ A.‎1‎‎6‎ B.‎1‎‎4‎ C.‎1‎‎3‎ D.‎‎1‎‎2‎ ‎9. 如图，在‎△ABC中，BC＝‎120‎，高AD＝‎60‎，正方形EFGH一边在BC上，点E，F分别在AB，AC上，AD交EF于点N，则AN的长为（ ）‎ A.‎15‎ B.‎20‎ C.‎25‎ D.‎‎30‎ ‎10. 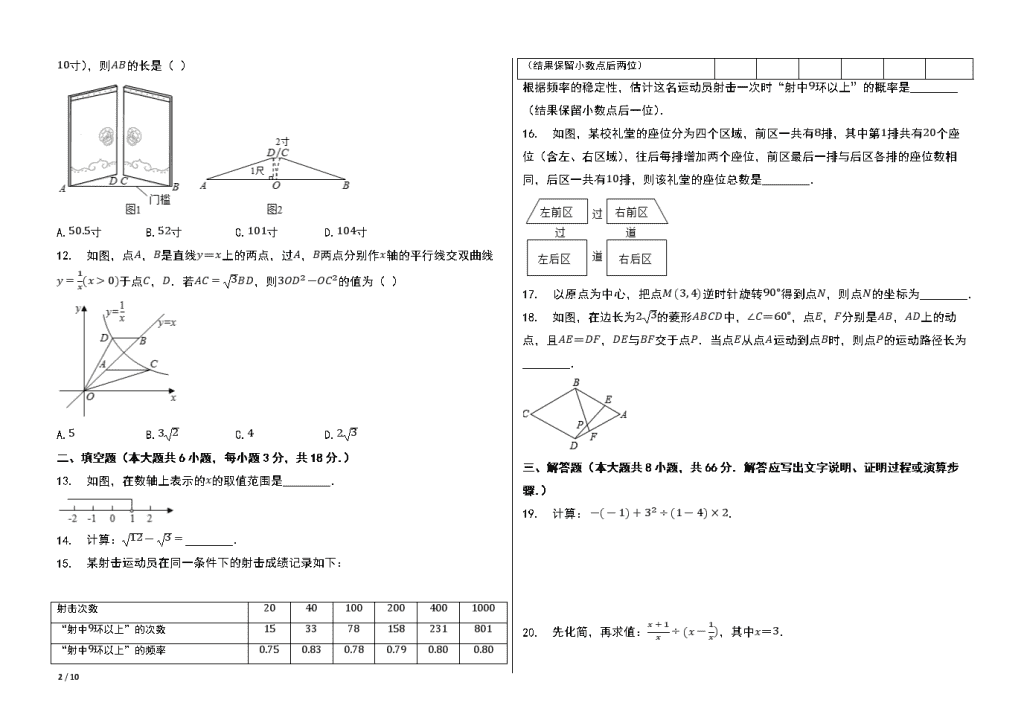甲、乙两地相距‎600km，提速前动车的速度为vkm/h，提速后动车的速度是提速前的‎1.2‎倍，提速后行车时间比提速前减少‎20min，则可列方程为（ ）‎ A.‎600‎v‎-‎1‎‎3‎=‎‎600‎‎1.2v B.‎‎600‎v‎=‎600‎‎1.2v-‎‎1‎‎3‎ C.‎600‎v‎-20=‎‎600‎‎1.2v D.‎‎600‎v‎=‎600‎‎1.2v-20‎ ‎11. 《九章算术》是古代东方数学代表作，书中记载：今有开门去阃（读kǔn，门槛的意思）一尺，不合二寸，问门广几何？题目大意是：如图‎1‎、‎2‎（图‎2‎为图‎1‎的平面示意图），推开双门，双门间隙CD的距离为‎2‎寸，点C和点D距离门槛AB都为‎1‎尺（‎1‎尺＝‎ ‎ 10 / 10‎ ‎10‎寸），则AB的长是（ ）‎ A.‎50.5‎寸 B.‎52‎寸 C.‎101‎寸 D.‎104‎寸 ‎12. 如图，点A，B是直线y＝x上的两点，过A，B两点分别作x轴的平行线交双曲线y=‎1‎x(x>0)‎于点C，D．若AC=‎3‎BD，则‎3OD‎2‎-OC‎2‎的值为（ ）‎ A.‎5‎ B.‎3‎‎2‎ C.‎4‎ D.‎‎2‎‎3‎ 二、填空题（本大题共6小题，每小题3分，共18分．）‎ ‎13. 如图，在数轴上表示的x的取值范围是________．‎ ‎14. 计算：‎12‎‎-‎3‎=‎________．‎ ‎15. 某射击运动员在同一条件下的射击成绩记录如下：‎ 射击次数 ‎20‎ ‎40‎ ‎100‎ ‎200‎ ‎400‎ ‎1000‎ ‎“射中‎9‎环以上”的次数 ‎15‎ ‎33‎ ‎78‎ ‎158‎ ‎231‎ ‎801‎ ‎“射中‎9‎环以上”的频率 ‎（结果保留小数点后两位）‎ ‎0.75‎ ‎0.83‎ ‎0.78‎ ‎0.79‎ ‎0.80‎ ‎0.80‎ 根据频率的稳定性，估计这名运动员射击一次时“射中‎9‎环以上”的概率是________（结果保留小数点后一位）．‎ ‎16. 如图，某校礼堂的座位分为四个区域，前区一共有‎8‎排，其中第‎1‎排共有‎20‎个座位（含左、右区域），往后每排增加两个座位，前区最后一排与后区各排的座位数相同，后区一共有‎10‎排，则该礼堂的座位总数是________．‎ ‎17. 以原点为中心，把点M (3, 4)‎逆时针旋转‎90‎‎∘‎得到点N，则点N的坐标为________．‎ ‎18. 如图，在边长为‎2‎‎3‎的菱形ABCD中，‎∠C＝‎60‎‎∘‎，点E，F分别是AB，AD上的动点，且AE＝DF，DE与BF交于点P．当点E从点A运动到点B时，则点P的运动路径长为________．‎ 三、解答题（本大题共8小题，共66分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎19. 计算：‎-(-1)+‎3‎‎2‎÷(1-4)×2‎．‎ ‎20. 先化简，再求值：x+1‎x‎÷(x-‎1‎x)‎，其中x＝‎3‎．‎ ‎ 10 / 10‎ ‎21. 如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF．‎ ‎（1）求证：‎△ABC≅△DEF；‎ ‎（2）连接AD，求证：四边形ABED是平行四边形．‎ ‎22. 小手拉大手，共创文明城．某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况，通过发放问卷进行测评，从中随机抽取‎20‎份答卷，并统计成绩（成绩得分用x表示，单位：分），收集数据如下：‎ ‎90 82 99 86 98 96 90 100 89 83 87 88 81 90 93 100 100 96 92 100‎ 整理数据：‎ ‎80≤x<85‎ ‎85≤x<90‎ ‎90≤x<95‎ ‎95≤x<100‎ ‎3‎ ‎4‎ a ‎8‎ 分析数据：‎ 平均分 中位数 众数 ‎92‎ b c 根据以上信息，解答下列问题：‎ ‎（1）直接写出上述表格中a，b，c的值；‎ ‎（2）该校有‎1600‎名家长参加了此次问卷测评活动，请估计成绩不低于‎90‎分的人数是多少？‎ ‎（3）请从中位数和众数中选择一个量，结合本题解释它的意义．‎ ‎23. 如图，一艘渔船位于小岛B的北偏东‎30‎‎∘‎方向，距离小岛‎40nmile的点A处，它沿着点A的南偏东‎15‎‎∘‎的方向航行．‎ ‎ 10 / 10‎ ‎（1）渔船航行多远距离小岛B最近（结果保留根号）？‎ ‎（2）渔船到达距离小岛B最近点后，按原航向继续航行‎20‎6‎nmile到点C处时突然发生事故，渔船马上向小岛B上的救援队求救，问救援队从B处出发沿着哪个方向航行到达事故地点航程最短，最短航程是多少（结果保留根号）？‎ ‎24. 倡导垃圾分类，共享绿色生活．为了对回收的垃圾进行更精准的分类，某机器人公司研发出A型和B型两款垃圾分拣机器人，已知‎2‎台A型机器人和‎5‎台B型机器人同时工作‎2h共分拣垃圾‎3.6‎吨，‎3‎台A型机器人和‎2‎台B型机器人同时工作‎5h共分拣垃圾‎8‎吨．‎ ‎（1）‎1‎台A型机器人和‎1‎台B型机器人每小时各分拣垃圾多少吨？‎ ‎（2）某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分拣机器人，这批机器人每小时一共能分拣垃圾‎20‎吨．设购买A型机器人a台‎(10≤a≤45)‎，B型机器人b台，请用含a的代数式表示b；‎ ‎（3）机器人公司的报价如下表：‎ 型号 原价 购买数量少于‎30‎台 购买数量不少于‎30‎台 A型 ‎20‎万元/台 原价购买 打九折 B型 ‎12‎万元/台 原价购买 打八折 在（2）的条件下，设购买总费用为w万元，问如何购买使得总费用w最少？请说明理由．‎ ‎25. 如图，在‎△ACE中，以AC为直径的‎⊙O交CE于点D，连接AD，且‎∠DAE＝‎∠ACE，连接OD并延长交AE的延长线于点P，PB与‎⊙O相切于点B．‎ ‎ 10 / 10‎ ‎（1）求证：AP是‎⊙O的切线；‎ ‎（2）连接AB交OP于点F，求证：‎△FAD∽△DAE；‎ ‎（3）若tan∠OAF=‎‎1‎‎2‎，求AEAP的值．‎ ‎26. 如图‎1‎，在平面直角坐标系中，直线l‎1‎‎:y＝x+1‎与直线l‎2‎‎:x＝‎-2‎相交于点D，点A是直线l‎2‎上的动点，过点A作AB⊥‎l‎1‎于点B，点C的坐标为‎(0, 3)‎，连接AC，BC．设点A的纵坐标为t，‎△ABC的面积为s．‎ ‎（1）当t＝‎2‎时，请直接写出点B的坐标；‎ ‎（2）s关于t的函数解析式为s=‎1‎‎4‎t‎2‎‎+bt-‎5‎‎4‎,t<-1t>5‎a(t+1)(t-5),-1