2013年浙江温州中考数学试卷及答案(解析版) 10页

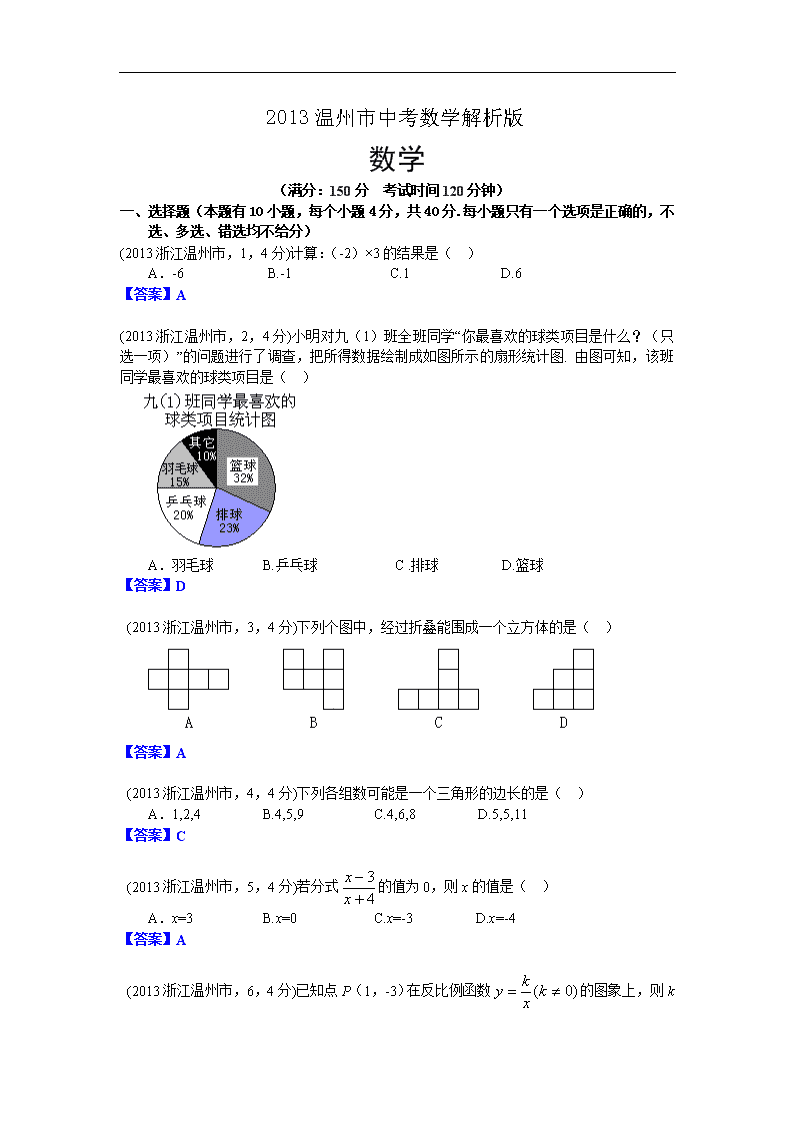
‎2013温州市中考数学解析版 数学 ‎ （满分：150分 考试时间120分钟）‎ 一、选择题（本题有10小题，每个小题4分，共40分.每小题只有一个选项是正确的，不选、多选、错选均不给分）‎ ‎(2013浙江温州市，1，4分)计算：（-2）×3的结果是（ ）‎ A．-6 B.-1 C.1 D.6‎ ‎【答案】A ‎(2013浙江温州市，2，4分)小明对九（1）班全班同学“你最喜欢的球类项目是什么？（只选一项）”的问题进行了调查，把所得数据绘制成如图所示的扇形统计图. 由图可知，该班同学最喜欢的球类项目是（ ）‎ A．羽毛球 B.乒乓球 C .排球 D.篮球 ‎【答案】D ‎ (2013浙江温州市，3，4分)下列个图中，经过折叠能围成一个立方体的是（ ）‎ ‎【答案】A ‎ (2013浙江温州市，4，4分)下列各组数可能是一个三角形的边长的是（ ）‎ A．1,2,4 B.4,5,‎9 C.4,6,8 D.5,5,11‎ ‎【答案】C ‎ (2013浙江温州市，5，4分)若分式的值为0，则x的值是（ ）‎ A．x=3 B.x=0 C.x=-3 D.x=-4‎ ‎【答案】A ‎ (2013浙江温州市，6，4分)已知点P（1，-3）在反比例函数的图象上，则k 的值是（ ）‎ A.3 B.-3 C. D.‎ ‎【答案】B ‎(2013浙江温州市，7，4分)如图，在⊙O中，OC⊥弦AB于点C，AB=4，OC=1，则OB的长是（ ）‎ A. B. C. D.‎ ‎【答案】B ‎(2013浙江温州市，8，4分)如图，在△ABC中，∠C=90°，AB=5，BC=3，则sinA的值是（ ）‎ A． B. C. D.‎ ‎【答案】C ‎(2013浙江温州市，9，4分)如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC.已知AE=6，，则EC的长是（ ）‎ A.4.5‎‎ B.8 C.10.5 D.14‎ ‎【答案】B ‎(2013浙江温州市，10，4分)在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作弧，如图所示，若AB=4，AC=2，，则S3-S4的值是（ ）‎ A. B. C. D.‎ ‎【答案】D 二、填空题（本题有6小题，每小题5分，共30分）‎ ‎ (2013浙江温州市，11，5分)因式分解：m2‎-5m= .‎ ‎【答案】m（m-5）‎ ‎(2013浙江温州市，12，5分)在演唱比赛中，5位评委给一位歌手打分如下：8.2分，8.3分，7.8分，7.7分，8.0分，则这位歌手的平均分是 分.‎ ‎【答案】8.0‎ ‎ (2013浙江温州市，13，5分)如图，直线a，b被直线c所截. 若a∥b，∠1=40°，∠2=70°，则∠3= 度.‎ ‎【答案】110‎ ‎ (2013浙江温州市，14，5分)方程x2-2x-1=0的解是 .‎ ‎【答案】‎ ‎ (2013浙江温州市，15，5分)如图，在平面直角坐标系中△ABC的两个顶点A，B的坐标分别为（-2,0），（-1,0），BC⊥x轴. 将△ABC以y轴为对称轴对称变换，得到△A′B′C′（A和A′，B和B′，C和C′分别是对应顶点）.直线y=x+b经过点A，C′，则点C′的坐标是 .‎ ‎【答案】（1,3）‎ ‎(2013浙江温州市，16，5分)一块矩形木板，它的右上角有一个圆洞. 现设想将它改造成火锅餐桌桌面，要求木板大小不变，且使圆洞的圆心在矩形桌面的对角线交点上，木工师傅想到了一个巧妙的办法，他测量了PQ与圆洞的切点K到点B的距离及相关的数据（单位：cm）后，从点N沿折线NF—FM（NF∥BC，FM∥AB）切割，如图1所示.图2中的矩形EFGH 是切割后的两块木板拼接成符合要求的矩形桌面示意图（不重叠，无缝隙，不计损耗），则CN，AM的长分别是 .‎ ‎【答案】‎18cm，31cm 三、解答题（本题有8小题，共80分.解答需写出必要的文字说明、演算步骤或证明过程）‎ ‎(2013浙江温州市，17(1)，5分)计算：‎ 解：=2+（－1）+1=3.‎ ‎(2013浙江温州市，17(2)，5分)化简：(1+a)(1-a)+a（a-3）‎ 解：（1+a）（1-a）+a（a-3）=1-a2+a2-3a=1-3a.‎ ‎ (2013浙江温州市，18，8分)如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E.‎ ‎（1）求证：△ACD≌△AED；‎ ‎（2）若∠B=30°，CD=1，求BD的长.‎ ‎（1）证明1：∵AD平分∠CAB.‎ ‎ ∴∠CAD=∠EAD.‎ ‎ ∵DE⊥AB, ∠C=90°，‎ ‎ ∴∠ACD=∠AED=90°.‎ ‎ 又∵AD=AD，‎ ‎ ∴△ACD≌△AED(AAS).‎ ‎ 证明2：∵∠C=90°，∴AC⊥CD，‎ ‎ ∵DE⊥AB, ∴CD=DE，‎ ‎ ∵AD=AD,∴△ACD≌△AED(HL).‎ ‎ (2)解：∵△ACD≌△AED ‎ ∴DE=CD=1.‎ ‎ ∵∠B=30°, ∠DEB=90°,‎ ‎ ∴BD=2DE=2.‎ ‎(2013浙江温州市，19，9分)如图，在方格纸中，△ABC的三个顶点和点P都在小方格的顶点上.按要求画一个三角形，使它的顶点在方格的顶点上.‎ ‎（1）将△ABC平移，使点P落在平移后的三角形内部，在图甲中画出示意图；‎ ‎（2）以点C为旋转中心，将△ABC旋转，使点P落在旋转后的三角形内部，在图乙中画出示意图.‎ 解：(1)答案如图示：‎ ‎(2)答案如图示：‎ ‎ (2013浙江温州市，20，10分)如图，抛物线y=a(x-1)2+4与x轴交于点A，B，与y轴交于点C. 过点C作CD∥x轴交抛物线的对称轴于点D，连结BD. 已知点A的坐标为（-1,0）.‎ ‎（1）求抛物线的解析式；‎ ‎（2）求梯形COBD的面积.‎ 解：（1）把A（-1,0）代入y=a(x-1)2+4，‎ ‎ 得0=‎4a+4，‎ ‎ ∴a=-1，‎ ‎ ∴y=-(x-1)2+4.‎ ‎ （2）令x=0，得y=3，‎ ‎ ∴OC=3.‎ ‎ ∵抛物线y=-(x-1)2+4的对称轴是直线x=1，‎ ‎ ∴CD=1.‎ ‎ ∵A（-1,0）‎ ‎ ∴B（3,0），‎ ‎ ∴OB=3.‎ ‎ ∴‎ ‎(2013浙江温州市，21，10分)一个不透明的袋中装有5个黄球，13个黑球和22个红球，它们除颜色外都相同.‎ ‎（1）求从袋中摸出一个球是黄球的概率；‎ ‎（2）现在袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后，使从袋中摸出一个球是黄球的概率不小于。问至少取出了多少黑球？‎ 解：（1）摸出一个球是黄球的概率.‎ ‎ （2）设取出x个黑球. 由题意，得.‎ ‎ 解得.‎ ‎ ∴x的最小正整数解是x=9.‎ ‎ 答：至少取出9个黑球.‎ ‎ (2013浙江温州市，22，10分)如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB.延长DA与⊙O的另一个交点为E，连结AC，CE.‎ ‎（1）求证：∠B=∠D；‎ ‎（2）若AB=4，BC-AC=2，求CE的长.‎ 解：（1）证明：∵AB为⊙O的直径，‎ ‎ ∴∠ACB=90°，‎ ‎ ∴AC⊥BC,‎ ‎ ∵DC=CB ‎ ∴AD=AB，‎ ‎ ∴∠B=∠D.‎ ‎ （2）设BC=x，则AC=x-2.‎ ‎ 在Rt△ABC中，AC2+BC2=AB2，‎ ‎ ∴（x-2）2+x2=4，‎ ‎ 解得（舍去），‎ ‎ ∵∠B=∠E，∠B=∠D，‎ ‎ ∴∠D=∠E，‎ ‎ ∴CD=CE，‎ ‎ ∵CD=CB ‎ ∴CE=CB=1+.‎ ‎(2013浙江温州市，23，10分)某校举办八年级学生数学素养大赛。比赛共设四个项目：七巧板拼图、趣题巧解、数学应用、魔方复原，每个项目得分都按一定百分比折算后记入总分. 下表为甲、乙、丙三位同学的得分情况（单位：分）.‎ 七巧板拼图 趣题巧解 数学应用 魔方复原 甲 ‎66‎ ‎89‎ ‎86‎ ‎68‎ 乙 ‎66‎ ‎60‎ ‎80‎ ‎68‎ 丙 ‎66‎ ‎80‎ ‎90‎ ‎68‎ ‎(1) 比赛后，甲猜测七巧板拼图、趣题巧解、数学应用、魔方复原这四项得分分别按10﹪,40﹪,20﹪,30﹪折算记入总分.根据猜测，求出甲的总分；‎ ‎(2) 本次大赛组委会最后决定，总分为80分以上（包括80分）的学生获一等奖. 现获悉乙、丙的总分分别是70分，80分，甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分. 问甲能否获得这次比赛一等奖？‎ 解：(1)甲的总分：66×10﹪+89×40﹪+86×20﹪+68×30﹪=79.8（分）.‎ ‎ （2）设趣题巧解所占的百分比为x，数学应用所占的百分比为y.‎ ‎ 由题意，得 ‎ 解得 ‎ ∴甲的总分：20+89×0.3+86×0.4=81.1>80.‎ ‎ ∴甲能获一等奖.‎ ‎(2013浙江温州市，24，14分)如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6,0），B（0，8）.点C的坐标为（0，m），过点C作CE⊥AB于点E. 点D为x轴上一动点，连结CD，DE，以CD，DE为边作□CDEF.‎ ‎（1）当00时.‎ ‎ (ⅰ)当0CP，显然不存在满足条件的m的值.‎ ‎ （Ⅱ）当m=0时，即点C与原点O重合（如图4），满足题意.‎ ‎ （Ⅲ）当m<0时，‎ ‎ （ⅰ）当点E与点A重合时（如图5）.‎ ‎ 易证△COA∽△AOB，‎ ‎∴.‎ 解得.‎ ‎ （ⅱ）当点E与点A不重合时（如图6）.‎ ‎ ‎ ‎ .‎ ‎ 由题意，得OG=CP，‎ ‎ ∴，‎ ‎ 解得.‎ ‎ 综上所述，m的值为或0或或.‎