图形的放大与缩小,位似变换教案(2) 3页

‎3.5 图形的放大与缩小，位似变换 ‎【教学目标】‎ ‎1.知识与技能：感受图形的放大与缩小，了解位似变换的概念与性质，会利用位似变换将一个图像放大或缩小。‎ ‎2.过程与方法：在有关知识的学习和运用过程中，发展学生的数学应用意识，进一步培养学生动手操作的良好习惯。‎ ‎3.情感态与价值观：利用图形的相似解决一些实际问题，使学生体会数学来源于实践同时又指导实践这一真理，激发学生学习数学的热情。‎ ‎【教学重点难点】‎ 重点：位似变换的原理 难点：利用位似变换将一个图形放大或缩小 ‎【教法与学法指导】‎ 学生自学——合作交流——教师释疑——检测反馈 ‎【教学过程】‎ 一、创设情景、导入新课 观察：‎ ‎1.下面这一组图有何特点？‎ 图1‎ ‎2.下面的一组图片是形状相同的图形,在图片①上取一点A,它与另一图片(如图片②)上的相应点B之间的连线是否经过镜头P的中心?在图片上换其它的点试一试,还有类似的结论吗?‎ 3‎ ‎①‎ ‎②‎ ‎③‎ ‎④‎ ‎⑤‎ C D ‎ 图2‎ 二、合作交流、解读探究 知识点1：位似图形 如果两个图形不仅相似,而且每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形, 这个点叫做位似中心, 这时的相似比又称为位似比。‎ 探究：‎ 在如图（3）中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系?‎ A B C D E B1‎ A1‎ C1‎ D1‎ E1‎ 学生通过实践测量，然后讨论 知识点2： 位似图形的性质 两个位似图形上每一对对应点与位似中心都在一条直线上，并且新图形与原图形对应点到位似中心的距离都等于位似比。‎ 知识点3：位似图形的画法 依据位似图形的性质，可以将一个图形放大或缩小。放大则位似比大于1，缩小则位似比在0～1之间。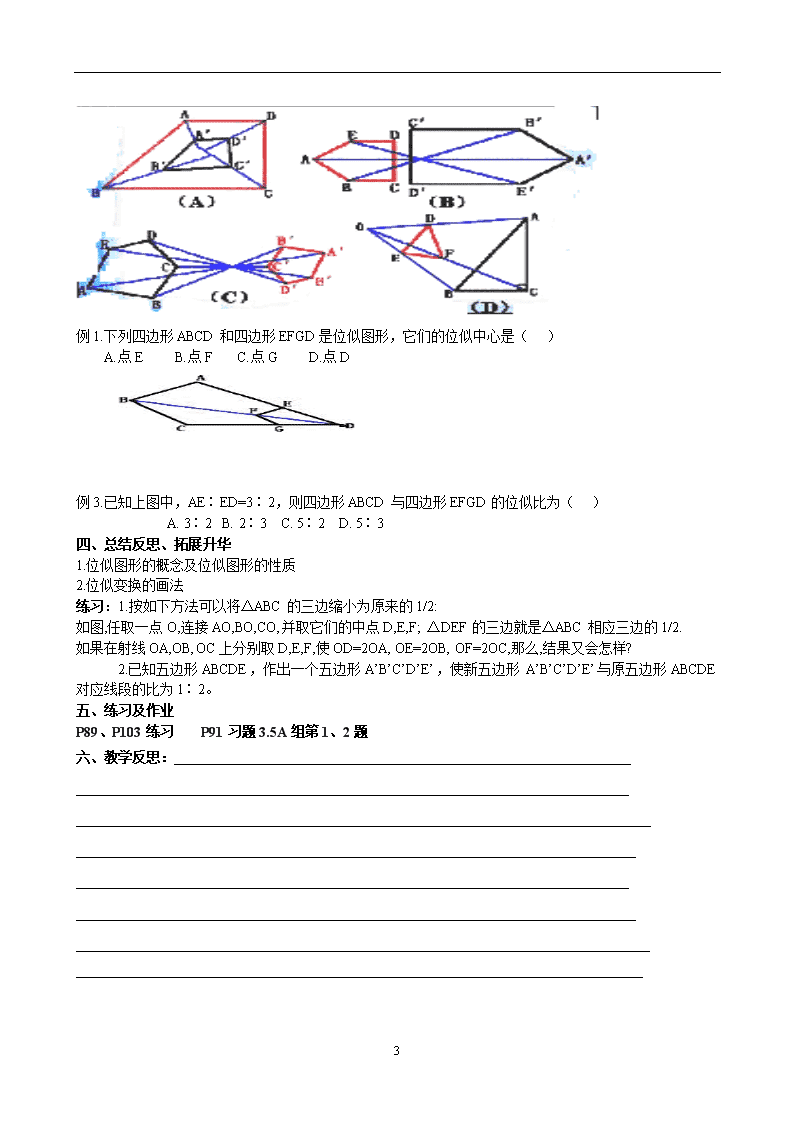‎ 三、课堂检测、迁移应用 例1.下列每组的两个图形，是位似图形的是（ ）‎ 3‎ 例1.下列四边形ABCD和四边形EFGD是位似图形，它们的位似中心是（    ） 　　A.点E         B.点F       C.点G         D.点D 　　　‎ 例3.已知上图中，AE∶ED=3∶2，则四边形ABCD与四边形EFGD的位似比为（    ） A. 3∶2   B. 2∶3    C. 5∶2    D. 5∶3‎ 四、总结反思、拓展升华 ‎1.位似图形的概念及位似图形的性质 ‎2.位似变换的画法 练习：1.按如下方法可以将△ABC的三边缩小为原来的1/2:‎ 如图,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F; △DEF的三边就是△ABC相应三边的1/2. ‎ 如果在射线OA,OB,OC上分别取D,E,F,使OD=2OA, OE=2OB, OF=2OC,那么,结果又会怎样?‎ ‎ 2.已知五边形ABCDE，作出一个五边形A’B’C’D’E’，使新五边形 A’B’C’D’E’与原五边形ABCDE对应线段的比为1∶2。‎ 五、练习及作业 P89、P103练习 P91习题3.5A组第1、2题 六、教学反思： ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 3‎