新人教数学九年级下册：达标训练（27-1图形的相似） 5页

达标训练 基础•巩固 1.在比例尺为 1∶40 000 的工程示意图上，于年 9 月 1 日正式通车的南京地铁一号线(奥体中心至迈皋桥段) 的长度约为 54.3 cm，它的实际长度约为() A.0.217 2 km B.2.172 km C.21.72 km D.217.2 km 思路解析：可设这两地的实际距离为 x cm (要注意统一单位)，根据比例尺= 实际距离 图上距离 得 54.3∶x=1∶40 000，解得：x=2 172 000(cm)=21.75(km). 答案：C 2 如图 27.3-4，在△ABC 中，D、E 分别是 AB、AC 的中点，BC=12，则DE 与 BC 的比是() 图 27.1-4 A.1∶4B.1∶3C.1∶2D.2∶3 思路解析：DE 是△ABC 的中位线，三角形的中位线平行于第三边，并且等于第三边的一半. 答案：C 3.(1)若 5.0 f e d c b a ，则 fdb eca   23 23 =__________； (2)若 kxy z xz y zy x  ,则 k=__________. 思路解析：连等式时，可用比例系数(即公比)的办法解决. (1)由 5.0 f e d c b a ，得到 a=0.5b，c=0.5d，e=0.5f，代入 fdb eca   23 23 中解得; (2)用“若 n m d c b a   =k(b+d+…+n≠0)，则 kndb mca     ”，但要注意只有当x+y+z≠0 时才成立. 本题中，还需考虑 x+y+z=0 的情况，此时 x=-(y+z)，y=-(z+x)，z=-(x+y)，所以 k=-1. 答案：(1)0.5,(2) 2 1 或-1 4.如图 27.1-5，在同一时刻，小明测得他的影长为 1 米，距他不远 处的一棵槟榔树的影长为 5 米，已知小 明的身高为 1.5 米，则这棵槟榔树的高是__________米. 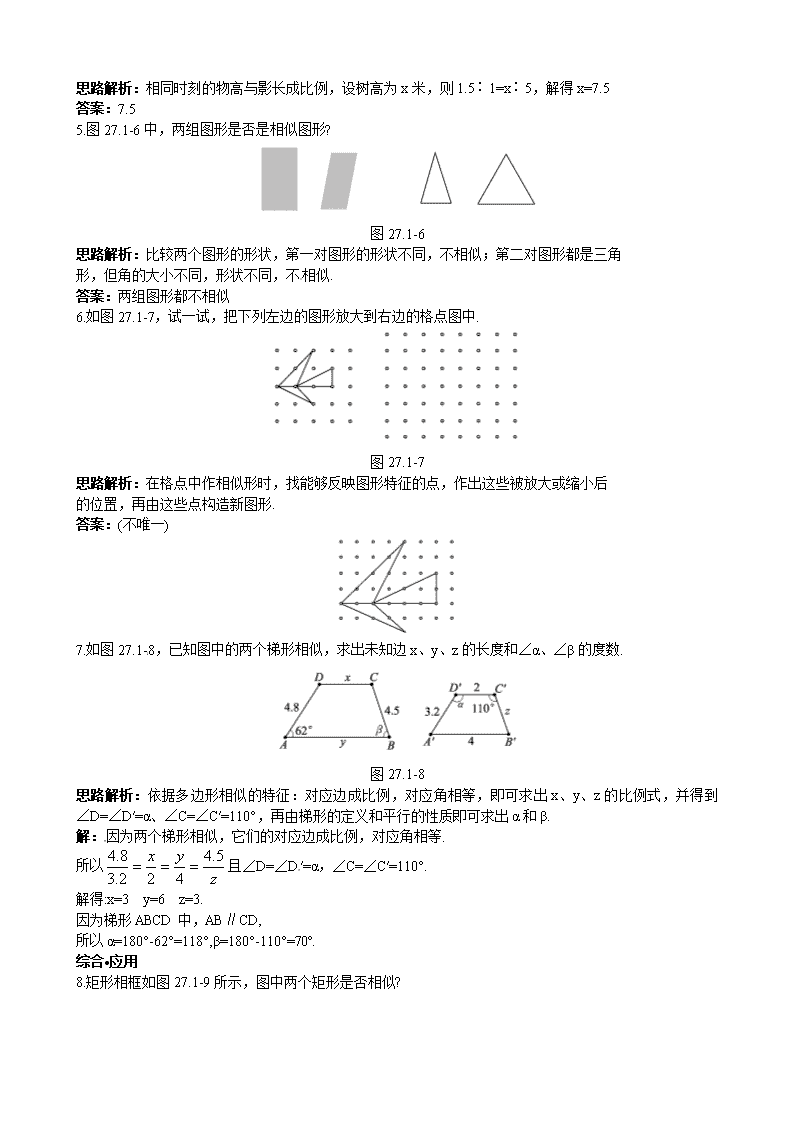图 27.1-5 思路解析：相同时刻的物高与影长成比例，设树高为 x 米，则 1.5∶1=x∶5，解得 x=7.5 答案：7.5 5.图 27.1-6 中，两组图形是否是相似图形? 图 27.1-6 思路解析：比较两个图形的形状，第一对图形的形状不同，不相似；第二对图形都是三角 形，但角的大小不同，形状不同，不 相似. 答案：两组图形都不相似 6.如图 27.1-7，试一试，把下列左边的图形放大到右边的格点图中. 图 27.1-7 思路解析：在格点中作相似形时，找能够反映图形特征的点，作出这些被放大或缩小后 的位置，再由这些点构造新图形. 答案：(不唯一) 7.如图 27.1-8，已知图中的两个梯形相似，求出未知边 x、y、z 的长度和∠α、∠β的度数. 图 27.1-8 思路解析：依据多边形相似的特征：对应边成比例，对应角相等，即可求出 x、y、z 的比例式，并得到 ∠D=∠D′=α、∠C=∠C′=110°，再由梯形的定义和平行的性质即可求出α和β. 解：因为两个梯形相似，它们的对应边成比例，对应角相等. 所以 z yx 5.4 422.3 8.4  且∠D=∠D′=α，∠C=∠C′=110°. 解得:x=3 y=6 z=3. 因为梯形 ABCD 中，AB∥CD, 所以α=180°-62°=118°,β=180°-110°=70°. 综合•应用 8.矩形相框如图 27.1-9 所示，图中两个矩形是否相似? 图 27.1-9 思路解析：矩形的四个角都是直角，所以这两个矩形的角都能对应相等；能不能相似关键就看边是否能对 应成比例了，不能只凭直觉了. 解：由图可知：大矩形的四条边长分别是 14、8、14、8； 而小矩形的长为：14-2-2=10，宽为：8-2-2=4，四条边分别是 10,4,10,4. ∵14∶10≠8∶4, ∴这两个矩形不相似. 9.判断下列各组线段是否成比例? (1)3 cm；5 cm；7 cm；4 cm； (2)12 mm；5 cm；15 mm；4 cm； (3)1 cm；5 mm；10 mm；2 cm. 思路解析：要解决此类问题,应先统一单位(当四条线段的长度单位不相同时)，把它们 按从小到大(或从大到小)的顺序进行排列，然后依次计算第一条与第二条、第三条与第四条线段的比，看 这两个比值是否相等；有时计算乘积要方便些，如果第一、四两个数的积等于第二三两个数的积，则四条 线段成比例，否则不成比例. 解：(1)四条线段按从小大的顺序排列为 3，4，5，7. ∵3×7≠4×5，即 3∶4≠5∶7， ∴3 cm,4 cm,5 cm,7 cm 这四条线段不成比例 (2)5 cm=50 mm,4 cm=40 mm,四条线段按从小大的顺序排列为 12，15，40，50. ∵12×50=15×40，即 12∶15=40∶50， ∴12 mm,5 cm,15 mm,4 cm 这四条线段成比例. (3)1 cm=10 mm,2 cm=20 mm, 四条线段按从小大的顺序排列为 5，10，10，20. ∵5×20=10×10，即 5∶10=10∶20， ∴5 mm,1 cm,10 mm,2 cm 这四条线段成比例. 10.试将一个正方形纸片(如图 27.1-10)分割为 8 个相似的小正方形. 图27.1-10 答案： 11.在如图 27.1-11 所示的相似四边形中，α比β大 15°，求未知边 x、y 的长度和角度α、β的大小. 图 27.1-11 思路解析：依据多边形相似的特征：对应边成比例，对应角相等，即可求出 x、y、α和β 解：因为两个四边形相似，它们的对应边成比例，对应角相等， 所以 12∶6=8∶y=x∶3.解得 y=4，x=6. 由α+β+115°=360°，α=β+15°， 得α=100°，β=85°. 回顾•展望 12.(浙江杭州模拟)我们已经学习了相似三角形,也知道:如果两个几何图形形状相同而大小不一定相同,我们 就把它们叫做相似图形.比如两个正方形,它们的边长 ,对角线等所有元素都对应成比例,就可以称它们为相 似图形. 现给出下列 4 对几何图形:①两个圆；②两个菱形；③两个长方形；④两个正六边形.请指出其中哪几对是 相似图形，哪几对不是相似图形，并简单地说明理由. 思路解析：根据相似形的定义，比较两个图形的对应边的比是否相等，对应角是否相等. 答：①两个圆是相似形.因为任何圆的形状相同； ②两个菱形不是相似形.因为两个菱形的对角线不对应成比例，两个菱形的形状不同； ③两个长方形不是相似形.因为两个长方形的边、对角线不对应成比例，两个长方形的形 状不同； ④两个正六边形是相似形.因为任何正六边形的形状相等. 13.(福建南平模拟)定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形. 探究： (1)如图甲，已知△ABC 中，∠C=90°，你能把△ABC 分割成 2 个与它自己相似的小直角三角形吗？若能， 请在图甲中画出分割线，并说明理由. (2)一般地，“任意三角形都是自相似图形”，只要顺次连结三角形各边中点，则可将原三角形分割为四个都 与它自己相似的小三角形. 我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割，称为 1 阶分割(如图 1)； 把 1 阶分割得出的 4 个三角形再分别顺次连结它的各边中点所进行的分割，称为 2 阶分割(如图 2)，… 依次规则操作下去，n 阶分割后得到的每一个小三角形都是全等三角形(n 为正整数)，设此时小三角形的面 积为 Sn. ①若△DEF 的面积为 10 000，当 n 为何值时，21 时，请写出一个反映 Sn-1，Sn，Sn+1 之间关系的等式(不必证明) 图乙图 1(1 阶) 图 2(2 阶) 图 3(3 阶) 思路解析：本题是阅读理解题，n 阶分割实际是把原三角形分为 4n 个相同的小三角形， 所以每个小三角形的面积是原三角形的 n4 1 . 解：(1)正确画出分割线 CD(如图，过点 C 作 CD⊥AB，垂足为 D，CD 即是满足要求的分割 线) 理由：∵∠B=∠B，∠CDB=∠ACB=90°， ∴△BCD∽△ACB. (2)①△DEF 经 n 阶分割所得的小三角形的个数为 n4 1 . ∴ Sn= n4 10000 . 当 n=5 时，S5= 54 10000 ≈9.77; 当 n=6 时，S6= 64 10000 ≈2.44; 当 n=7 时，S7= 74 10000 ≈0.61. ∴当 n=6 时，2＜S6＜3. ② 2 nS =Sn-1×Sn+1.