2012年江苏省宿迁市中考数学试卷（含答案） 8页

‎2012年江苏省宿迁市中考数学试卷 一、选择题（共8小题，每小题3分，满分24分，每小题共四个选项，有且只有一个正确的）‎ ‎1．-8的绝对值是（　A　）‎ A． 　　　　　B． 　　　　　 C． 　　　　　 D．‎ ‎2．在平面直角坐标系中，点（3，－2）关于原点对称点的坐标是（　C　）‎ A．（３，２）　 B．（－３，－２） 　C．（－3，2）　 D．（－３，－２） ‎ ‎ 3．计算（-a）2•a3的结果是（　A　）‎ A．a5 　　　　　　B．a6 　　　　　C．-a5 　　　　　　D．-a6 ‎ ‎　‎ ‎4．如图是一个用相同的小立方体搭成的几何体的三视图，则组成这个几何体的小立方体的个数是（　C　）‎ A．2 　　　　B．3 　　　C．4 　　　D．5 ‎ ‎5．绿豆在相同条件下的发芽试验，结果如下表所示：‎ 每批粒数n ‎100‎ ‎300‎ ‎400‎ ‎600‎ ‎1000‎ ‎2000‎ ‎3000‎ 发芽的粒数m ‎96‎ ‎282‎ ‎382‎ ‎570‎ ‎948‎ ‎1912‎ ‎2850‎ 发芽的频数 ‎0.960‎ ‎0.940‎ ‎0.955[来源:学_科_网Z_X_X_K]‎ ‎0.950‎ ‎0.948‎ ‎0.956‎ ‎0.950‎ 则绿豆发芽的概率估计值是 （　B　）‎ A．0.96 　　　　　　B．0.95 　　　　　　C．0.94 　　　　　　D．0.90 ‎ ‎6．已知一组数据：1，3，5，5，6，则这组数据的方差是（　D　）‎ A．16　　　　　　　 B．5 　　　　　　　C．4 　　　　　　　D．3.2 ‎ ‎　‎ ‎7．若⊙O1，⊙O2的半径分别是r1=2，r2=4，圆心距d=5，则这两个圆的位置关系是（　B　）‎ A．内切　　　　　　 B．相交 　　　　　C．外切 　　　　　　D．外离 ‎ ‎8．在平面直角坐标系中，若将抛物线y=2x2-4x+3先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后所得抛物线的顶点坐标是（　D　）‎ A．（-2，3） 　　　　B．（-1，4）　　　　 C．（1，4） 　　　　D．（4，3） ‎ 二、填空题（共10小题，每小题3分，满分30分）‎ ‎9．-5的相反数是 5 。‎ ‎10．使 在实数范围内有意义，x的取值范围是 x ≥ 2 。‎ ‎11．已知点E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点，若AC⊥BD，且AC≠BD，则四边形EFGH的形状是 矩形 （填“梯形”“矩形”或“菱形”）‎ ‎12．分解因式：ax2-ay2= a（x+y）（x-y）.‎ ‎13．不等式组 的解集是 1＜x＜2 .‎ ‎14．如图，SO，SA分别是圆锥的高和母线，若SA=12cm，∠ASO=30°，则这个圆锥的侧面积是 72π cm2．‎ ‎ 15．如图，将一张矩形纸片ABCD沿EF折叠，使顶点C，D分别落在点C′，D′处，C′E交AF于点G，若∠CEF=70°，则∠GFD′= 40 °．‎ ‎16．在平面直角坐标系中，若一条平行于x轴的直线l分别交双曲线和于A，B两点，P是x轴上的任意一点，则△ABP的面积等于 4 .‎ ‎17．如图，已知P是线段AB的黄金分割点，且PA＞PB，若S1表示PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，则S1 = S2．（填“＞”“=”或“＜”）‎ ‎18．按照如图所示的方法排列黑色小正方形地砖，则第14个图案中黑色小正方形地砖的块数是 365 .‎ 三、解答题（共10小题，满分96分解题时，应写出必要的文字说明，证明过程或演算步骤）‎ ‎19．计算：‎ 解：原式 ‎20．解方程： ‎ 解：方程的两边同乘（x-1）（x+1），得 x-1+x+1=0，‎ 解得x=0．‎ 检验：把x=0代入（x-1）（x+1）=-1≠0，即x=0是原分式方程的解．‎ 则原方程的解为：x=0．‎ ‎21．求代数式（a+2b）（a-2b）+（a+2b）2-4ab的值，其中a=1，b= ‎ 解：原式=a2-4b2+a2+4ab+4b2-4ab=2a2，‎ 当a=1，b=时，‎ 原式=2×12=2‎ ‎22．某学校抽查了某班级某月10天的用电量，数据如下表（单位：度）； 度数 8 9 10 13 14 15 天数 1 1 2 3 1 2 ‎ ‎（1）这10天用电量的众数是 13度 ，中位数是 13度 ，极差是 7度 ；‎ ‎（2）求这个班级平均每天的用电量；‎ ‎（3）已知该校共有20个班级，该月共计30天，试估计该校该月总的用电量． ‎ 解：（1）13度出现了3次，最多，故众数为13度；‎ 第5天和第天的用电量均是13度，故中位数为13度；‎ 极差为：15-8=7度；‎ ‎（2）平均用电量为：（8+9+10×2+13×3+14+15×2）÷10=12度；‎ ‎（3）总用电量为20×12×30=7200度．‎ ‎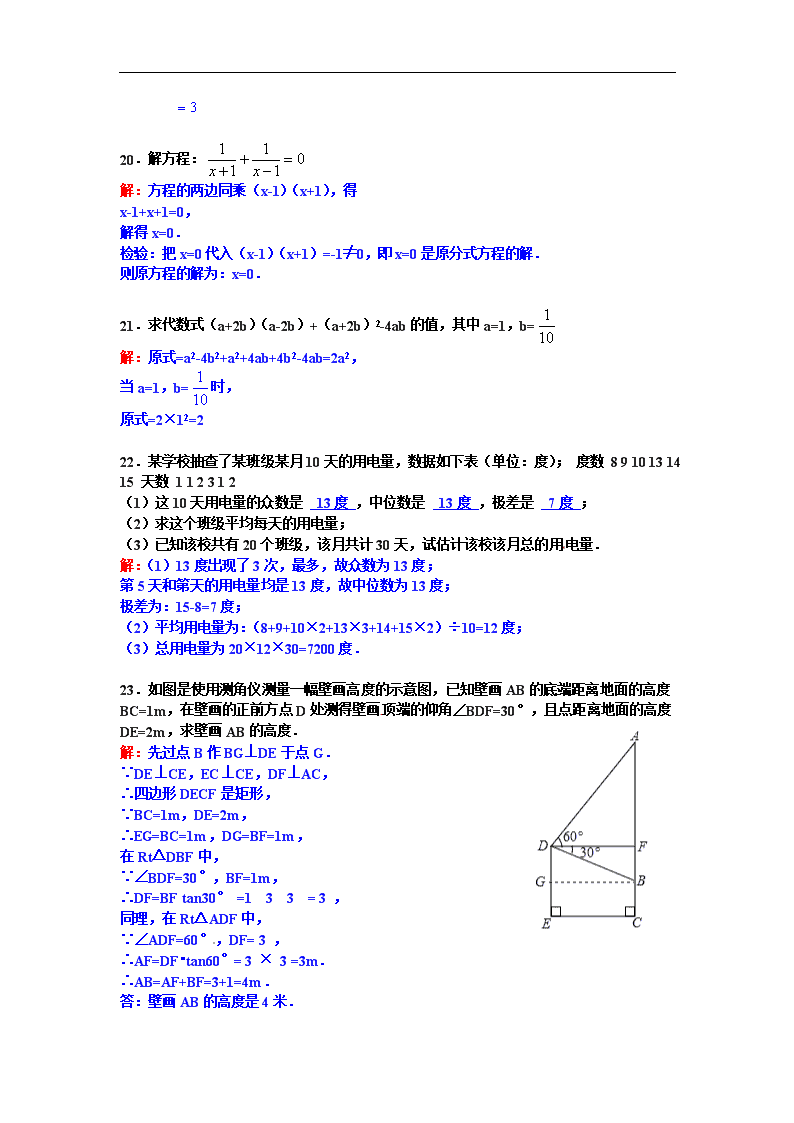23．如图是使用测角仪测量一幅壁画高度的示意图，已知壁画AB的底端距离地面的高度BC=1m，在壁画的正前方点D处测得壁画顶端的仰角∠BDF=30°，且点距离地面的高度DE=2m，求壁画AB的高度． [来源:学,科,网Z,X,X,K]‎ 解：先过点B作BG⊥DE于点G．‎ ‎∵DE⊥CE，EC⊥CE，DF⊥AC，‎ ‎∴四边形DECF是矩形，‎ ‎∵BC=1m，DE=2m，‎ ‎∴EG=BC=1m，DG=BF=1m，‎ 在Rt△DBF中，‎ ‎∵∠BDF=30°，BF=1m，‎ ‎∴DF=BF tan30° =1 3 3 = 3 ，‎ 同理，在Rt△ADF中，‎ ‎∵∠ADF=60°，DF= 3 ，‎ ‎∴AF=DF•tan60°= 3 × 3 =3m．‎ ‎∴AB=AF+BF=3+1=4m．‎ 答：壁画AB的高度是4米．‎ ‎24．有四部不同的电影，分别记为A，B，C，D．‎ ‎（1）若甲从中随机选择一部观看，则恰好是电影A的概率是 ；‎ ‎（2）若甲从中随机选择一部观看，乙也从中随机选择一部观看，求甲、乙两人选择同一部电影的概率． ‎ 解：（1）∵有四部不同的电影，恰好是电影A的只有1种情况，‎ ‎∴恰好是电影A的概率是：．‎ 故答案为： ； （2）画树状图得： ‎ ‎∵共有16种等可能的结果，甲、乙两人选择同一部电影的有4种情况，‎ ‎∴甲、乙两人选择同一部电影的概率为： ．‎ ‎25．学校组织学生乘汽车去自然保护区野营，先以60km/h的速度走平路，后又以30km/h的速度爬坡，共用了6.5h；汽车以40km/h的速度下坡，又以50km/h的速度走平路，共用了6h，问平路和坡路各有多远？ ‎ 解：设平路有x千米，坡路有y千米，由题意得：‎ ‎ ，解得： ，‎ 答：平路和坡路各有150米、120米．‎ ‎26．如图，在四边形ABCD中，∠DAB=∠ABC=90°，CD与以AB为直径的半圆相切于点E，EF⊥AB于点F，EF交BD于点G，设AD=a，BC=b．‎ ‎（1）求CD的长度（用a，b表示）；‎ F ‎（2）求EG的长度（用a，b表示）；‎ ‎（3）试判断EG与FG是否相等，并说明理由．‎ 解：（1）∵AB为半圆的直径，∠DAB=∠ABC=90°，‎ ‎∴DA、BC为半圆O的切线，‎ 又∵CD与以AB为直径的半圆相切于点E，‎ ‎∴DE=DA=a，CE=CB=b，‎ ‎∴CD=a+b；‎ ‎（2）∵EF⊥AB，‎ ‎∴EG∥BC，‎ ‎∴EG：BC=DE：DC，即EG ：b=a ：（a+b），‎ ‎∴ ；‎ ‎（3）EG与FG相等．理由如下：‎ ‎∵EG∥BC，‎ ‎∴ ，即 ①，‎ 又∵GF∥AD，‎ ‎∴，即 ②，‎ ‎①+②得，‎ 而，‎ ‎∴，‎ ‎∴ ，‎ ‎∴EG=FG．‎ ‎27．（1）如图1，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=∠‎ ABC（0°＜∠CBE＜∠ABC）．以点B为旋转中心，将△BEC按逆时针旋转∠ABC，得到△BE′A（点C与点A重合，点E到点E′处）连接DE′，求证：DE′=DE．‎ ‎（2）如图2，在△ABC中，BA=BC，∠ABC=90°，D，E是AC边上的两点，且满足∠DBE=∠ABC（0°＜∠CBE＜45°）．‎ 求证：DE2=AD2+EC2．‎ 证明（1）：∵∠DBE=∠ABC，‎ ‎∴∠ABD+∠CBE=∠DBE=∠ABC，‎ ‎∵△ABE′由△CBE旋转而成，‎ ‎∴BE=BE′，∠ABE′=∠CBE，‎ ‎∴∠DBE′=∠DBE，‎ 在△DBE与△DBE′中，‎ ‎∵ BE=BE′ ∠DBE=∠DBE′ BD=BD ，‎ ‎∴△DBE≌△DBE′，‎ ‎∴DE′=DE； （2）如图所示：把△CBE旋转90°，连接DE′，[来源:学§科§网]‎ ‎∵BA=BC，∠ABC=90°，‎ ‎∴∠BAC=∠BCE=45°，‎ ‎∴图形旋转后点C与点A重合，CE与AE′重合，‎ ‎∴AE′=EC，‎ ‎∴∠E′AB=∠BCE=45°，‎ ‎∴∠DAE′=90°，‎ 在Rt△ADE′中，DE′2 =AE′2 + AD2，‎ ‎∵AE′=EC，‎ ‎∴DE′2=EC2+AD2，‎ 同（1）可得DE=DE′，‎ ‎∴DE′2=AD2+EC2．‎ ‎28．如图，在平面直角坐标系xOy中，已知直线l1：y=x与直线l2：y= -x+6相交于点M，直线l2与x轴相交于点N．[来源:Z*xx*k.Com]‎ ‎（1）求M，N的坐标．‎ ‎（2）矩形ABCD中，已知AB=1，BC=2，边AB在x轴上，矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动，设矩形ABCD与△OMN的重叠部分的面积为S，移动的时间为t（从点B与点O重合时开始计时，到点A与点N重合时计时开始结束）．直接写出S与自变量t之间的函数关系式（不需要给出解答过程）．‎ ‎（3）在（2）的条件下，当t为何值时，S的值最大？并求出最大值．‎ 解：（1）解方程组 ，‎ 解得： ，‎ 则M的坐标是：（4 ，2）．‎ 在解析式y=-x+6中，令y=0，解得：x=6，则N的坐标是：（6，0）． （2）当0≤t≤1时，重合部分是一个三角形，OB=t，则高是t，则面积是 ×t• t= t2；‎ 当1＜t≤4时，重合部分是直角梯形，梯形的高是1，下底是： t，上底是：（t-1），根据梯形的面积公式可以得到：；‎ 当4＜t≤5时，过M作x轴的垂线，则重合部分被垂线分成两个直角梯形，两个梯形的下底都是2，上底分别是：-t+6和（t-1），根据梯形的面积公式即可求得 ‎ ；‎ 当5＜t≤6时，重合部分是直角梯形，与当1＜t≤4时，重合部分是直角梯形的计算方法相同，则S=7-2t；‎ 当6＜t≤7时，重合部分是直角三角形，则与当0≤t≤1时，解法相同，可以求得．‎ 则：‎ ‎（3）在0≤t≤1时，函数的最大值是：；‎ 当1＜t≤4，函数值y随x的增大而增大，则当x=4时，取得最大值是： ；‎ 当4＜t≤5时，是二次函数，对称轴x= ，则最大值是：- ；‎ 当5＜t≤6时，函数y随t的增大而减小，因而函数值一定小于 ；‎ 同理，当6＜t≤7时，y随t的增大而减小，因而函数值小于 ．‎ 总之，函数的最大值是： ．‎