【35套试卷合集】内蒙古呼伦贝尔市名校2019-2020学年数学九上期末模拟试卷含答案 10页

‎2019-2020 学年九上数学期末模拟试卷含答案 一、选择题（共 10 小题，每小题 3 分，共 30 分）在每小题列出的四个选项中，只有一个是正确的，请把 答题卡对应题目所选的选项涂黑．‎ ‎1．（ 3 分）在 Rt△ ABC中，∠ C=90°， BC=4， AC=3，则 cosA的值是（ ）‎ A． B． C． D．‎ x ‎2．（ 3 分）如果﹣ 1 是方程 2﹣ 3x+k=0 的一个根，则常数 k 的值为（ ）‎ A． 4 B． 2 C．﹣ 4 D．﹣ 2‎ ‎3．（ 3 分）下列四个几何体中，主视图与左视图相同的几何体有（ ）‎ A． 1 个 B． 2 个 C． 3 个 D． 4 个 ‎4．（ 3 分）点 A（﹣ 3， y1）、 B（﹣ 1，y2）、C（ 1，y3）都在反比例函数 Y= （ k＜ 0）的图象上，则 y1、 y2、 y3 的大小关系是（ ）‎ A． y1＜ y2＜ y3 B． y3＜ y2 ＜y1 C． y3＜ y1＜ y2 D． y2 ＜y1＜ y3‎ ‎5．（ 3 分）如图，在△ ABC中， D， E 分别是 AB 和 AC 上的点，且 DE∥ BC， = ， DE= 6，则 BC 的长 为（ ）‎ A． 8 B． 9 C． 10 D． 12‎ ‎6．（ 3 分）下列说法正确的是（ ） A．对角线相等且互相垂直的四边形是菱形 B．对角线互相平分的四边形是正方形 C．对角线互相垂直的四边形是平行四边形 D．对角线相等且互相平分的四边形是矩形 ‎2﹣ 6x+k=0 有两个不相等的实根，则 k 的范围是（ ）‎ ‎7．（ 3 分）关于 x 的一元二次方程 9x A． k＜ 1 B． k＞ 1 C． k≤ 1 D． k≥ 1‎ ‎8．（ 3 分）如图，无法保证△ ADE 与△ ABC相似的条件是（ ）‎ A．∠ 1=∠C B．∠ A=∠ C C．∠ 2=∠ B D．‎ ‎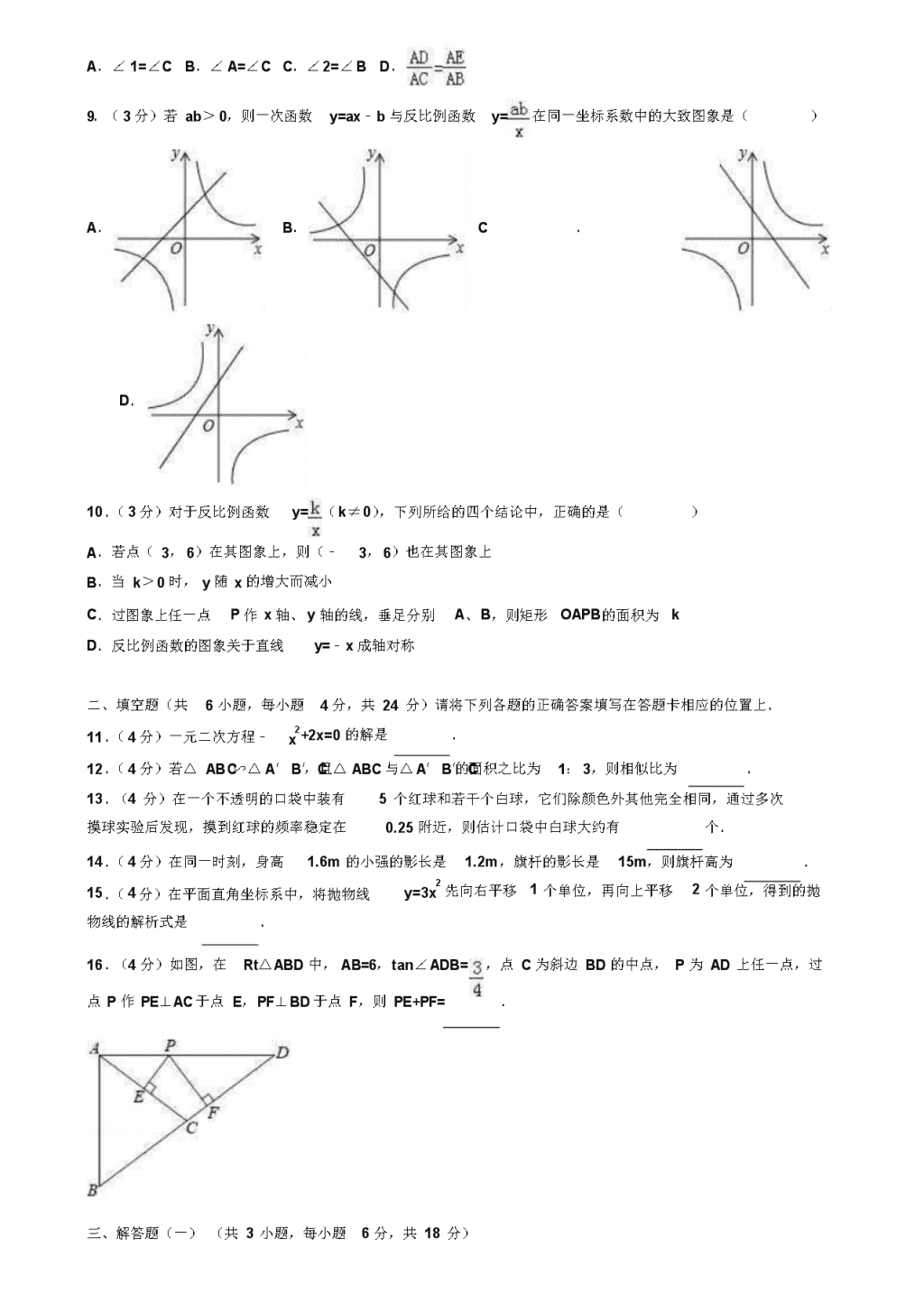9．（ 3 分）若 ab＞ 0，则一次函数 y=ax﹣ b 与反比例函数 y= 在同一坐标系数中的大致图象是（ ）‎ A． B． C ．‎ D．‎ ‎10 ．（ 3 分）对于反比例函数 y= （ k≠ 0），下列所给的四个结论中，正确的是（ ）‎ A．若点（ 3， 6）在其图象上，则（﹣ 3， 6）也在其图象上 B．当 k＞ 0 时， y 随 x 的增大而减小 C．过图象上任一点 P 作 x 轴、 y 轴的线，垂足分别 A、 B，则矩形 OAPB的面积为 k D．反比例函数的图象关于直线 y=﹣ x 成轴对称 二、填空题（共 6 小题，每小题 4 分，共 24 分）请将下列各题的正确答案填写在答题卡相应的位置上．‎ x ‎11 ．（ 4 分）一元二次方程﹣ 2+2x=0 的解是 ．‎ ‎12 ．（ 4 分）若△ ABC∽△ A′ B′，C且′△ ABC 与△ A′ B′的C面′积之比为 1： 3，则相似比为 ．‎ ‎13 ．（ 4 分）在一个不透明的口袋中装有 5 个红球和若干个白球，它们除颜色外其他完全相同，通过多次 摸球实验后发现，摸到红球的频率稳定在 0.25 附近，则估计口袋中白球大约有 个．‎ ‎14 ．（ 4 分）在同一时刻，身高 1.6m 的小强的影长是 1.2m ，旗杆的影长是 15m，则旗杆高为 ．‎ ‎2‎ ‎15 ．（ 4 分）在平面直角坐标系中，将抛物线 y=3x 物线的解析式是 ．‎ ‎先向右平移 1 个单位，再向上平移 2 个单位，得到的抛 ‎16 ．（ 4 分）如图，在 Rt△ ABD 中， AB=6， tan∠ ADB= ，点 C 为斜边 BD 的中点， P 为 AD 上任一点，过 点 P 作 PE⊥ AC 于点 E， PF⊥ BD 于点 F，则 PE+PF= ．‎ 三、解答题（一） （共 3 小题，每小题 6 分，共 18 分）‎ ‎17．（ 6 分）计算： ﹣ 2tan45 °﹣ cos30 °+4sin30 ．°‎ ‎18 ．（ 6 分）如今上购物已经成为一种时尚， 某店 “双十一 ”全天交易额逐年增长， 2015 年交易额为 40 万元，‎ ‎2017 年交易额为 48.4 万元，求 2015 年至 2017 年 “双十一 ”交易额的年平均增长率？‎ ‎19 ．（ 6 分）如图，有一转盘中有 A、B 两个区域， A 区域所对的圆心角为 120 °，让转盘自由转动两次．利 用树状图或列表求出两次指针都落在 A 区域的概率．‎ 四、解答题（二） （共 3 小题，每小题 7 分，共 21 分）‎ ‎20．（ 7 分）如图，反比例函数 y= （ k≠ 0）的图象经过点 A（ 1， 2）和 B（ 2， n），‎ ‎（ 1）以原点 O 为位似中心画出△ A1B1 O，使 = ；‎ ‎（ 2）在 y 轴上是否存在点 P，使得 PA+PB 的值最小？若存在，求出 P 的坐标；若不存在，请说明理由．‎ ‎21 ．（ 7 分）如图，某人在 D 处测得山顶 C 的仰角为 37 °，向前走 100 米来到山脚 A 处，测得山坡 AC 的坡 度为 i=1：0.5，求山的高度（不计测角仪的高度，参考数据： sin37 °≈ 0.60，cos37°≈ 0 .80，tan37°≈ 0.75）．‎ ‎22 ．（ 7 分）如图，点 D 是 Rt△ ABC 斜边 AB 的中点，过点 B、 C 分别作 BE∥ CD， CE∥ BD．‎ ‎（ 1）若∠ A=60°， AC= ，求 CD 的长；‎ ‎（ 2）求证： BC⊥ DE．‎ 五、解答题（三） （ 共 3 小题，每小题 9 分，共 27 分）‎ x ‎23 ．（ 9 分）如图，抛物线 y=﹣ 2+bx+c 经过直线 y=﹣ x+3 与坐标轴的两个交点 A、B，与 x 轴的另一个交点 为 C，顶点为 D．‎ ‎（ 1）求抛物线的解析式；‎ ‎（ 2）画出抛物线的图象；‎ ‎（ 3）在 x 轴上是否存在点 N 使△ ADN 为直角三角形？若存在， 求出点 N 的坐标； 若不存在， 请说明理由．‎ ‎24 ．（ 9 分）如图， AB⊥ BC， DC⊥ BC，E 是 BC 上一点，使得 AE⊥ DE；‎ ‎（ 1）求证：△ ABE∽△ ECD；‎ ‎（ 2）若 AB=4， AE=BC=5，求 CD 的长；‎ ‎（ 3）当△ AED∽△ ECD时，请写出线段 AD、 AB、 CD 之间数量关系，并说明理由．‎ ‎25．（ 9 分）如图，在矩形 ABCD中， AB=6cm， BC=8cm，如果点 E 由点 B 出发沿 BC方向向点 C 匀速运动， 同时点 F 由点 D 出发沿 DA 方向向点 A 匀速运动，它们的速度分别为每秒 2cm 和 1cm， FQ⊥ BC，分别交 AC、 BC 于点 P 和 Q，设运动时间为 t 秒（ 0＜ t ＜4）．‎ ‎（ 1）连接 EF，若运动时间 t= 时， EF⊥ AC；‎ ‎（ 2）连接 EP，当△ EPC的面积为 3cm2 时，求 t 的值；‎ ‎（ 3）若△ EQP∽△ ADC，求 t 的值．‎ 参考答案与试题解析 一、选择题（共 10 小题，每小题 3 分，共 30 分）在每小题列出的四个选项中，只有一个是正确的，请把 答题卡对应题目所选的选项涂黑．‎ ‎1．（ 3 分）在 Rt△ ABC中，∠ C=90°， BC=4， AC=3，则 cosA的值是（ ）‎ A． B． C． D．‎ ‎【解答】解：∵∠ C=90°， BC=4， AC=3，‎ ‎∴ AB= =5，‎ ‎∴ cosA= ， 故选： B．‎ x ‎2．（ 3 分）如果﹣ 1 是方程 2﹣ 3x+k=0 的一个根，则常数 k 的值为（ ）‎ A． 4 B． 2 C．﹣ 4 D．﹣ 2‎ ‎【 解答】解：∵﹣ 1 是方程 x2﹣ 3x+k=0 的一个根，‎ ‎∴（﹣ 1） 2﹣ 3×（﹣ 1） +k=0，解得 k=﹣ 4， 故选： C．‎ ‎3．（ 3 分）下列四个几何体中，主视图与左视图相同的几何体有（ ）‎ A． 1 个 B． 2 个 C． 3 个 D． 4 个 ‎【解答】解：①正方体的主视图与左视图都是正方形；‎ ‎②球的主视图与左视图都是圆；‎ ‎③圆锥主视图与左视图都是三角形；‎ ‎④圆柱的主视图和左视图都是长方形； 故选： D．‎ ‎4．（ 3 分）点 A（﹣ 3， y1）、 B（﹣ 1，y2）、C（ 1，y3）都在反比例函数 Y= （ k＜ 0）的图象上，则 y1、 y2、 y3 的大小关系是（ ）‎ A． y1＜ y2＜ y3 B． y3＜ y2 ＜y1 C． y3＜ y1＜ y2 D． y2 ＜y1＜ y3‎ ‎【解答】解：∵ A（﹣ 3， y1）， B（﹣ 1， y2），C（ 1，y3）都在反比例函数 y= （ k＜ 0）的图象上，‎ ‎∴﹣ 3y1=k，﹣ y2=k， y3=k，‎ ‎∴ y1=﹣ k， y2=﹣ k， y3=k， 而 k＜ 0，‎ ‎∴ y3＜ y1＜ y2．‎ 故选： C．‎ ‎5．（ 3 分）如图，在△ ABC中， D， E 分别是 AB 和 AC上的点，且 DE∥ BC， = ， DE=6，则 BC 的长为 ‎（ ）‎ A． 8 B． 9 C． 10 D． 12‎ ‎【解答】解：∵ DE∥ BC，‎ ‎∴△ ADE∽△ ABC，‎ ‎∴ = ，‎ 又∵ = ， DE=6，‎ ‎∴ = ，‎ ‎∴ BC=10，‎ 故选： C．‎ ‎6．（ 3 分）下列说法正确的是（ ） A．对角线相等且互相垂直的四边形是菱形 B．对角线互相平分的四边形是正方形 C．对角线互相垂直的四边形是平行四边形 D．对角线相等且互相平分的四边形是矩形 ‎【解答】解：利用排除法分析四个选项： A、菱形的对角线互相垂直且平分，故 A 错误； B、对角线互相平分的四边形式应该是平行四边形，故 B 错误；‎ C、对角线互相垂直的四边形并不能断定为平行四边形，故 C 错误；‎ D、对角线相等且互相平分的四边形是矩形，故 D 正确． 故选： D．‎ ‎7．（ 3 分）关于 x 的一元二次方程 9x ‎2﹣ 6x+k=0 有两个不相等的实根，则 k 的范围是（ ）‎ A． k＜ 1 B． k＞ 1 C． k≤ 1 D． k≥ 1‎ ‎【解答】解：∵关于 x 的一元二次方程 9x2﹣ 6x+k=0 有两个不相等的实根，‎ ‎∴△ =（﹣ 6） 2﹣ 4×9k＞ 0， 解得 k＜ 1．‎ 故选： A．‎ ‎8．（ 3 分）如图，无法保证△ ADE 与△ ABC相似的条件是（ ）‎ A．∠ 1=∠C B．∠ A=∠ C C．∠ 2=∠ B D．‎ ‎【解答】解：由图得：∠ A=∠ A，‎ ‎∴当∠ B=∠2 或∠ C=∠ 1 或 AE： AB=AD： AC 时，△ ABC与△ ADE 相似； 也可 AE： AD=AC： AB．‎ B 选项中∠ A 和∠ C 不是成比例的两边的夹角． 故选： B．‎ ‎9．（ 3 分）若 ab＞ 0，则一次函数 y=ax﹣ b 与反比例函数 y= 在同一坐标系数中的大致图象是（ ）‎ A． B． C ．‎ D．‎ ‎【解答】解： A、根据一次函数可判断 a＞ 0，b＜ 0，即 ab＜ 0，故不符合题意， B、根据一次函数可判断 a＜ 0， b＞ 0，即 ab＜ 0，故不符合题意，‎ C、根据一次函数可判断 a＜ 0， b＜ 0，即 ab＞ 0，根据反比例函数可判断 ab＞ 0，故符合题意， D、根据反比例函数可判断 ab＜0，故 不符合题意；‎ 故选： C．‎ ‎10 ．（ 3 分）对于反比例函数 y= （ k≠ 0），下列所给的四个结论中，正确的是（ ）‎ A．若点（ 3， 6）在其图象上，则（﹣ 3， 6）也在其图象上 B．当 k＞ 0 时， y 随 x 的增大而减小 C．过图象上任一点 P 作 x 轴、 y 轴的线，垂足分别 A、 B，则矩形 OAPB的面积为 k D．反比例函数的图象关于直线 y=﹣ x 成轴对称 ‎【解答】解： A、若点（ 3， 6）在其图象上，则（﹣ 3， 6）不在其图象上，故本选项不符合题意；‎ B、当 k＞ 0 时， y 随 x 的增大而减小，错误，应该是当 k＞ 0 时，在每个象限， y 随 x 的增大而减小；故本 选项不符合题意；‎ C、错误，应该是 过图象上任一点 P 作 x 轴、 y 轴的线，垂足分别 A、 B，则矩形 O APB 的面积为 | k| ；故 本选项不符合题意；‎ D、正确，本选项符合题意， 故选： D．‎ 二、填空题（共 6 小题，每小题 4 分，共 24 分）请将下列各题的正确答案填写在答题卡相应的位置上．‎ ‎2‎ ‎11 ．（ 4 分）一元二次方程﹣ x +2x=0 的解是 x=0 或 2 ．‎ ‎【解答】解：﹣ x2+2x=0，‎ x ‎2﹣ 2x=0， x（ x﹣ 2） =0， x=0 或 2，‎ 故答案为： x=0 或 2．‎ ‎12 ．（ 4 分）若△ ABC∽△ A′ B′，C且′△ ABC 与△ A′ B′的C面′积之比为 1： 3，则相似比为 1： ．‎ ‎【解答】解：∵△ ABC∽△ A′B′，C△′ ABC与△ A′B′的C面′积之比为 1： 3，‎ ‎∴△ ABC与△ A′B′的C相′似比为 1： ． 故答案为： 1： ．‎ ‎13 ．（ 4 分）在一个不透明的口袋中装有 5 个红球和若干个白球，它们除颜色外其他完全相同，通过多次 摸球实验后发现，摸到红球的频率稳定在 0.25 附近，则估计口袋中白球大约有 15 个．‎ ‎【解答】解：设白球个数为： x 个，‎ ‎∵摸到红色球的频率稳定在 0.25 左右，‎ ‎∴口袋中得到红色球的概率为 0.25，‎ ‎∴ = ， 解得： x=15，‎ 即白球的个数为 15 个，‎ 故答案为： 15 ．‎ ‎14 ．（ 4 分）在同一时刻，身高 1.6m 的小强的影长是 1.2m ，旗杆的影长是 15m，则旗杆高为 20m ．‎ ‎【解答】解：根据题意可得：设旗杆高为 x．‎ 根据在同一时刻身高与影长成比例可得： = ，‎ 故 x=20m． 故答案为 20．‎ y=3x ‎15 ．（ 4 分）在平面直角坐标系中，将抛物线 2 先向右平移 1 个单位，再向上平移 2 个 单位，得到的 抛物线的解析式是 y=3（ x﹣ 1） 2+2 ．‎ ‎【解答】解：∵抛物线 y=3x2 的顶点坐标为（ 0， 0），‎ ‎2‎ ‎∴抛物线 y=3x ‎向右平移 1 个单位，再向上平移 2 个单位得到的抛物线的顶点坐标为（ 1， 2），‎ ‎∴平移后抛物线的解析式为 y=3（ x﹣ 1） 2+2． 故答案是： y=3（ x﹣ 1） 2+2．‎ ‎16 ．（ 4 分）如图，在 Rt△ ABD 中， AB=6， tan∠ ADB= ，点 C 为斜边 BD 的中点， P 为 AD 上任一点，过 点 P 作 PE⊥ AC 于点 E， PF⊥ BD 于点 F，则 PE+PF= ．‎ ‎【解答】解：在 Rt△ABD 中，∵ tan ∠ ADB= = ，‎ ‎∴ AD= × 6=8，‎ ‎∴ BD= =10，‎ ‎∴ sinD= = ，‎ ‎∵点 C 为斜边 BD 的中点，‎ ‎∴ AC=BC=CD，‎ ‎∴∠ CAD=∠ D，‎ 在 Rt△ APE中， sin∠ EAP= = ，‎ ‎∴ PE= AP，‎ 在 Rt△ DPF中， sin∠ D= = ，‎ ‎∴ PF= PD，‎ ‎∴ PE+PF= （ AP+PD） = AD= ×8= ．‎