2020九年级数学下册 第1章 解直角三角形 专题分类突破五 三角函数应用的基本策略练习 7页

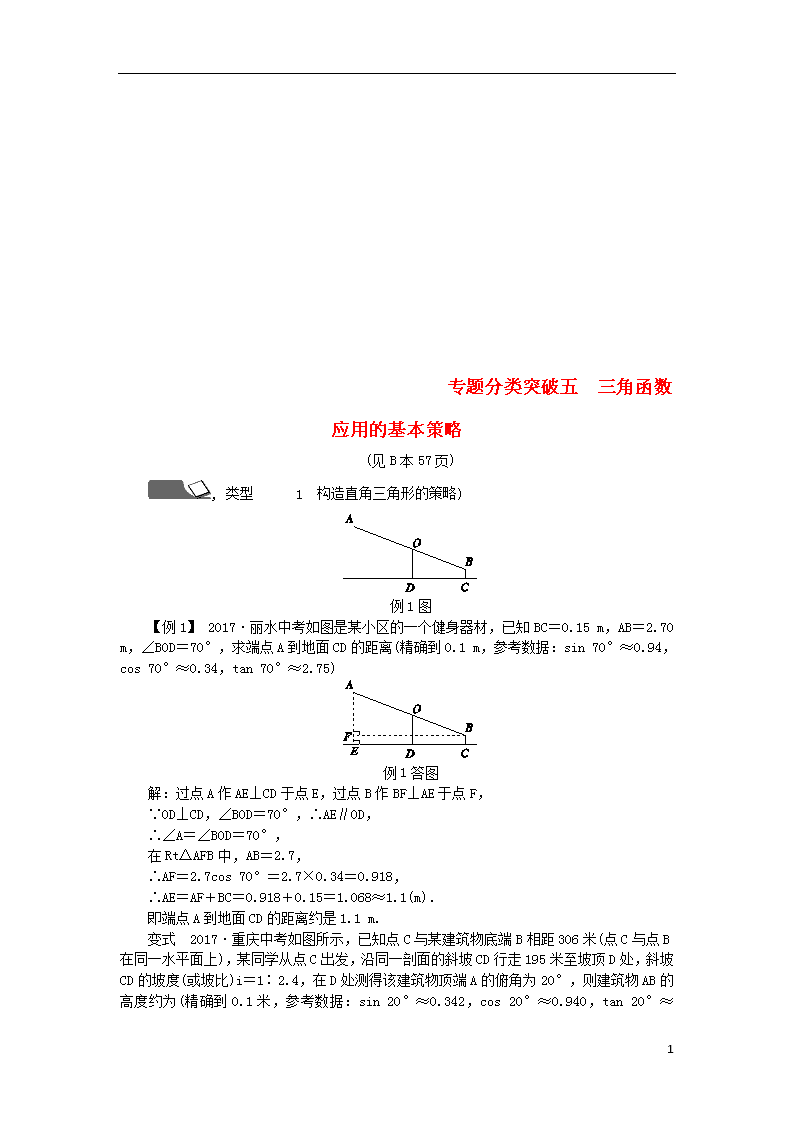
专题分类突破五　三角函数应用的基本策略 ‎(见B本57页)‎ ‎, 类型　　　1　构造直角三角形的策略)‎ 例1图 ‎【例1】 2017·丽水中考如图是某小区的一个健身器材，已知BC＝0.15 m，AB＝2.70 m，∠BOD＝70°，求端点A到地面CD的距离(精确到0.1 m，参考数据：sin 70°≈0.94，cos 70°≈0.34，tan 70°≈2.75)‎ 例1答图 解：过点A作AE⊥CD于点E，过点B作BF⊥AE于点F，‎ ‎∵OD⊥CD，∠BOD＝70°，∴AE∥OD，‎ ‎∴∠A＝∠BOD＝70°，‎ 在Rt△AFB中，AB＝2.7，‎ ‎∴AF＝2.7cos 70°＝2.7×0.34＝0.918，‎ ‎∴AE＝AF＋BC＝0.918＋0.15＝1.068≈1.1(m)．‎ 即端点A到地面CD的距离约是1.1 m.‎ 变式　2017·重庆中考如图所示，已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上)，某同学从点C出发，沿同一剖面的斜坡CD行走195米至坡顶D处，斜坡CD的坡度(或坡比)i＝1∶2.4，在D处测得该建筑物顶端A的俯角为20°，则建筑物AB的高度约为(精确到0.1米，参考数据：sin 20°≈0.342，cos 20°≈0.940，tan 20°≈‎ 7‎ ‎0.364)(　A　)‎ 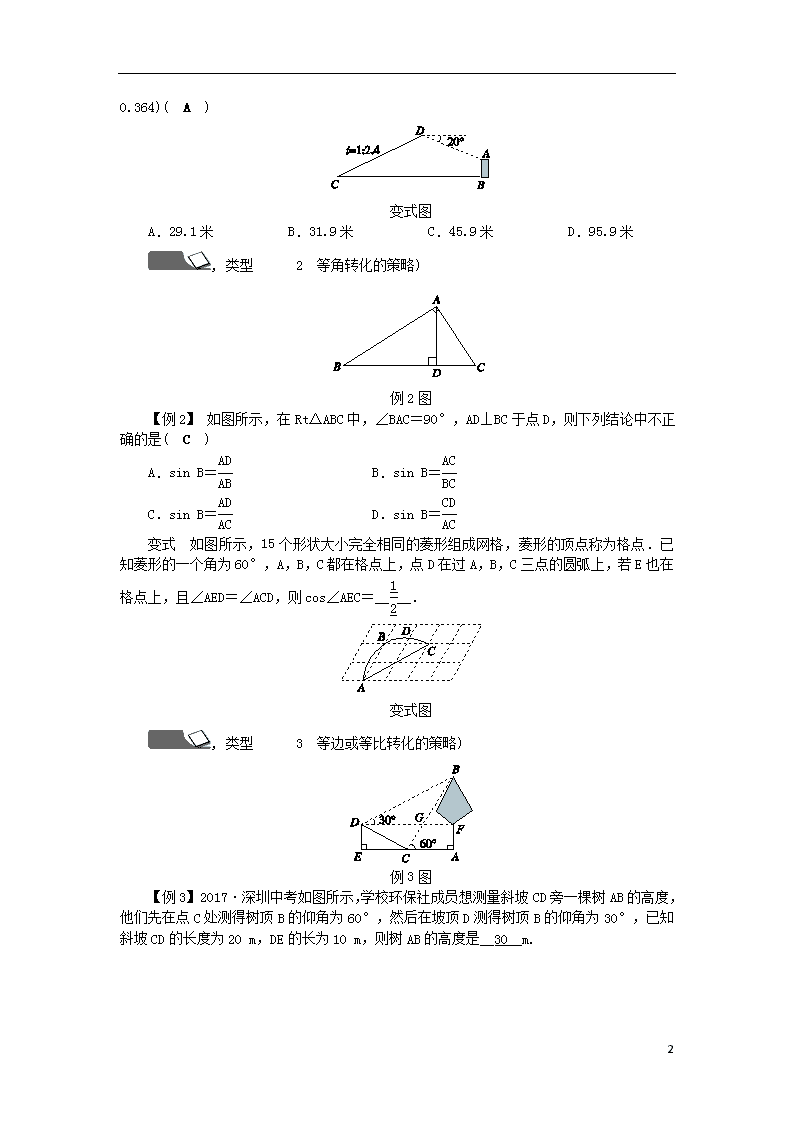变式图 A．‎29.1米 B．‎31.9米 C．‎45.9米 D．‎‎95.9米 ‎, 类型　　　2　等角转化的策略)‎ 例2图 ‎【例2】 如图所示，在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，则下列结论中不正确的是(　C　)‎ A．sin B＝ B．sin B＝ C．sin B＝ D．sin B＝ 变式　如图所示，15个形状大小完全相同的菱形组成网格，菱形的顶点称为格点．已知菱形的一个角为60°，A，B，C都在格点上，点D在过A，B，C三点的圆弧上，若E也在格点上，且∠AED＝∠ACD，则cos∠AEC＝____．‎ 变式图 ‎, 类型　　　3　等边或等比转化的策略)‎ 例3图 ‎【例3】 2017·深圳中考如图所示，学校环保社成员想测量斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为20 m，DE的长为10 m，则树AB的高度是__30__m.‎ 7‎ 变式图 变式　如图所示，AB是⊙O的直径，延长AB至P，使BP＝OB，BD垂直于弦BC，垂足为点B，点D在PC上．设∠PCB＝α，∠POC＝β.‎ 求证：tan α·tan＝.‎ 证明：连结AC，则∠A＝∠POC＝，‎ 变式答图 ‎∵AB是⊙O的直径，∴∠ACB＝90°，‎ ‎∴tan α＝，BD∥AC，∴∠PBD＝∠A，‎ ‎∵∠P＝∠P，‎ ‎∴△PBD∽△PAC，‎ ‎∴＝，∵PB＝OB＝OA，‎ ‎∴＝，‎ ‎∴tan a·tan ＝·＝＝.‎ 7‎ ‎1．Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O交AC于D，作直径DE，连结BE，若sin∠ACB＝，BC＝6，则BE＝(　B　)‎ A．6　　　 B.　　　 C.　　　 D．8‎ 第1题图 ‎　　　　第2题图 ‎2．2017·抚顺中考如图所示，某城市的电视塔AB坐落在湖边，数学老师带领学生隔湖测量电视塔AB的高度，在点M处测得塔尖点A的仰角∠AMB为22.5°，沿射线MB方向前进‎200米到达湖边点N处，测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°.则电视塔AB的高度为__100__米．(结果保留根号)‎ ‎3．2017·邵阳中考如图所示，运载火箭从地面L处垂直向上发射，当火箭到达A点时，从位于地面R处的雷达测得AR的距离是‎40 km，仰角是30°.n秒后，火箭到达B点，此时仰角是45°，则火箭在这n秒中上升的高度是__20－20__km.‎ 第3题图 ‎　　第4题图 ‎4．2017·绍兴中考如图所示，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB＝‎30 m.‎ ‎(1)则∠BCD的度数是__38°__；‎ ‎(2)求教学楼的高BD.(结果精确到‎0.1 m，参考数据：tan 20°≈0.36，tan 18°≈0.32)‎ 7‎ 第4题答图 解：(1)过点C作CE⊥BD，则有∠DCE＝18°，∠BCE＝20°，‎ ‎∴∠BCD＝∠DCE＋∠BCE＝18°＋20°＝38°.故答案为38°.‎ ‎(2)由题意，得CE＝AB＝‎30 m，‎ 在Rt△CBE中，BE＝CE·tan 20°≈10.80(m)，‎ 在Rt△CDE中，DE＝CE·tan 18°≈9.60(m)，‎ ‎∴教学楼的高BD＝BE＋DE＝10.80＋9.60＝20.4 m，‎ 则教学楼的高约为20.4 m.‎ ‎5．2017·衢州中考在直角坐标系中，过原点O及点A(8，0)，C(0，6)作矩形OABC，连结OB，点D为OB的中点，点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF.已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．‎ ‎(1)如图1，当t＝3时，求DF的长；‎ ‎(2)如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值．‎ 第5题图 解：(1)当t＝3时，点E为AB的中点，‎ ‎∵A(8，0)，C(0，6)，∴OA＝8，OC＝6，‎ ‎∵点D为OB的中点，∴DE∥OA，DE＝OA＝4，‎ ‎∵四边形OABC是矩形，∴OA⊥AB，∴DE⊥AB，‎ ‎∴∠OAB＝∠DEA＝90°，‎ 又∵DF⊥DE，∴∠EDF＝90°，‎ ‎∴四边形DFAE是矩形，‎ ‎∴DF＝AE＝3.‎ ‎(2)∠DEF的大小不变；理由如下：‎ 第5题答图 作DM⊥OA于点M，DN⊥AB于点N，如图所示．‎ 7‎ ‎∵四边形OABC是矩形，‎ ‎∴OA⊥AB，‎ ‎∴四边形DMAN是矩形，‎ ‎∴∠MDN＝90°，DM∥AB，DN∥OA，‎ ‎∴＝，＝，‎ ‎∵点D为OB的中点，‎ ‎∴M，N分别是OA，AB的中点，‎ ‎∴DM＝AB＝3，DN＝OA＝4，‎ ‎∵∠EDF＝90°，∴∠FDM＝∠EDN，‎ 又∵∠DMF＝∠DNE＝90°，‎ ‎∴△DMF∽△DNE，∴＝＝，‎ ‎∵∠EDF＝90°，∴tan∠DEF＝＝.‎ 7‎ 7‎