2020九年级数学下册 第2章 直线与圆的位置关系 2 7页

‎2.3　三角形的内切圆 ‎1．三角形内切圆定义：与三角形三边相切的圆叫做三角形的内切圆．‎ ‎2．三角形的内心是______________________交点．‎ ‎3．如图，⊙I内切于△ABC，切点分别为D，E，F.‎ ‎(1)∠BIC＝90°＋∠BAC；∠DEF＝90°－∠BAC；‎ ‎(2)△ABC三边长分别为a，b，c，⊙I的半径为r，则有S△ABC＝r(a＋b＋c)；‎ ‎(3)若∠ACB＝90°，AC＝b，BC＝a，AB＝c，则内切圆半径r＝CE＝.‎ A组　基础训练 ‎1．下列命题正确的是( )‎ A．三角形的内心到三角形三个顶点的距离相等 B．三角形的内心不一定在三角形的内部 C．等边三角形的内心，外心重合 D．一个圆一定有唯一一个外切三角形 ‎2．如图所示，⊙O是△ABC的内切圆，D，E，F是切点，∠A＝50°，∠C＝60°，则∠DOE等于( )‎ A．70° B．110° C．120° D．130°‎ 第2题图 7‎ ‎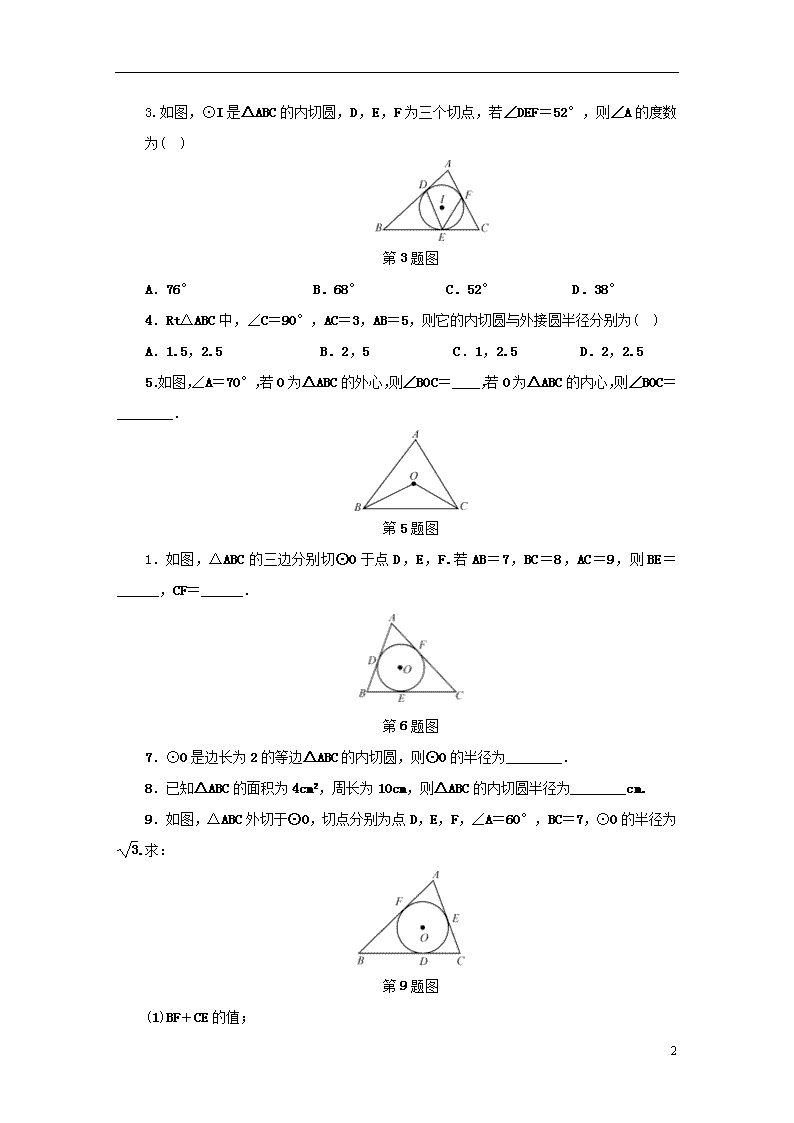3.如图，⊙I是△ABC的内切圆，D，E，F为三个切点，若∠DEF＝52°，则∠A的度数为( )‎ ‎　　　‎ 第3题图 A．76° B．68° C．52° D．38°‎ ‎4．Rt△ABC中，∠C＝90°，AC＝3，AB＝5，则它的内切圆与外接圆半径分别为( )‎ A．1.5，2.5 B．2，‎5 C．1，2.5 D．2，2.5‎ ‎5．如图，∠A＝70°，若O为△ABC的外心，则∠BOC＝____，若O为△ABC的内心，则∠BOC＝________．‎ 第5题图 1． 如图，△ABC的三边分别切⊙O于点D，E，F.若AB＝7，BC＝8，AC＝9，则BE＝______，CF＝______．‎ 第6题图 ‎7．⊙O是边长为2的等边△ABC的内切圆，则⊙O的半径为________．‎ ‎8．已知△ABC的面积为‎4cm2，周长为‎10cm，则△ABC的内切圆半径为________cm.‎ ‎9．如图，△ABC外切于⊙O，切点分别为点D，E，F，∠A＝60°，BC＝7，⊙O的半径为.求：‎ 第9题图 ‎(1)BF＋CE的值；‎ 7‎ ‎(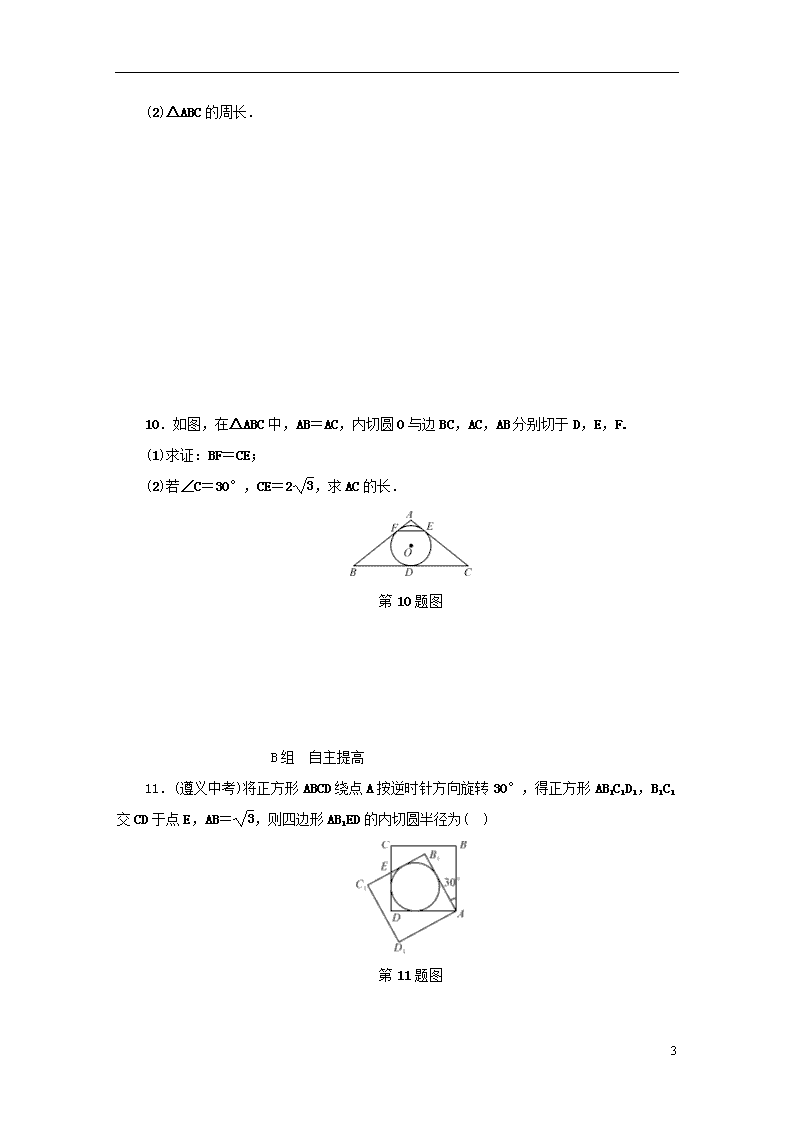2)△ABC的周长．‎ ‎10．如图，在△ABC中，AB＝AC，内切圆O与边BC，AC，AB分别切于D，E，F.‎ ‎(1)求证：BF＝CE；‎ ‎(2)若∠C＝30°，CE＝2，求AC的长．‎ 第10题图 B组　自主提高 11． ‎(遵义中考)将正方形ABCD绕点A按逆时针方向旋转30°，得正方形AB‎1C1D1，B‎1C1交CD于点E，AB＝，则四边形AB1ED的内切圆半径为( )‎ 第11题图 7‎ A. B. C. D. ‎12．如图，⊙O为△ABC的内切圆，∠C＝90°，AO的延长线交BC于点D，AC＝4，DC＝1，则⊙O的半径等于________．‎ 第12题图 ‎13．如图，点I是△ABC的内心，AI的延长线交边BC于点D，交△ABC的外接圆于点E.‎ ‎(1)求证：IE＝BE；‎ ‎(2)若IE＝4，AE＝8，求DE的长．‎ 第13题图 C组　综合运用 ‎14．如图，在锐角△ABC中，BC＝5，sin∠BAC＝，点I为三角形ABC的内心，AB＝BC，求AI的长．‎ 7‎ 第14题图 ‎2．3　三角形的内切圆 ‎【课堂笔记】‎ ‎2．三角形的三条角平分线的 ‎【课时训练】‎ ‎1－4.CBAC　‎ ‎5.140°　125°　‎ ‎6.3　5　‎ 7. 　‎ 8. ‎9．(1)∵△ABC外切于⊙O，切点分别为点D、E、F，∴BF＝BD，CE＝CD，∴BF＋CE＝BD＋CD＝BC＝7，所以BF＋CE的值是7.　‎ 第9题图 (2) 连结OE、OA.∵△ABC外切于⊙O，切点分别为点D、E、F，∴AE＝AF，∠OEA＝90°，∠‎ 7‎ OAE＝∠BAC＝30°，∴OA＝2OE＝2.由勾股定理得AE＝AF＝＝＝3，∴AB＋BC＋AC＝AF＋AE＋CE＋BF＋BC＝7＋7＋3＋3＝20，∴△ABC的周长是20.　‎ ‎10.(1)证明：∵AE，AF是⊙O的切线，∴AE＝AF，又∵AC＝AB，∴AC－AE＝AB－AF，∴CE＝BF，即BF＝CE；　(2)连结AO、OD，∵O是△ABC的内心，∴OA平分∠BAC，‎ 第10题图 ‎∵⊙O是△ABC的内切圆，D是切点，∴OD⊥BC；又∵AC＝AB，∴A、O、D三点共线，即AD⊥BC，∵CD、CE是⊙O的切线，∴CD＝CE＝2，∴在Rt△ACD中，由∠C＝30°，CD＝2，得AC＝＝＝4.　‎ ‎11.B　‎ ‎12. 　‎ ‎13.(1)连结IB.∵点I是△ABC的内心，∴∠BAD＝∠CAD，∠ABI＝∠IBD.又∵∠BIE＝∠BAD＋∠ABI，∴∠BIE＝∠CAD＋∠IBD＝∠DBE＋∠IBD＝∠IBE，∴BE＝IE；　‎ 第13题图 ‎(2)在△BED和△AEB中，∵∠EBD＝∠CAD＝∠EAB，∠BED＝∠AEB，∴△BED∽△AEB，∴＝.∵IE＝4，∴BE＝4.∵AE＝8，∴DE＝＝2.‎ ‎14．连结CI，BI，且延长BI交AC于点F，过点I作IG⊥BC于点G，IE⊥AB于点E.∵AB＝BC＝5，点I为△ABC的内心，∴BF⊥AC，AF＝CF.在Rt△ABF中，‎ 7‎ 第14题图 ‎∵sin∠BAC＝＝，∴BF＝4.∴AF＝＝3，∴AC＝6.∵点I是△ABC的内心，IE⊥AB，IF⊥AC，IG⊥BC，∴IE＝IF＝IG.∴S△ABC＝(AB＋AC＋BC)·IF＝AC·BF，∴IF＝＝＝，∴AI＝＝.‎ 7‎