初中数学中考复习课件章节考点专题突破：第五章图形性质1-23 矩形、菱形与正方形考点 22页

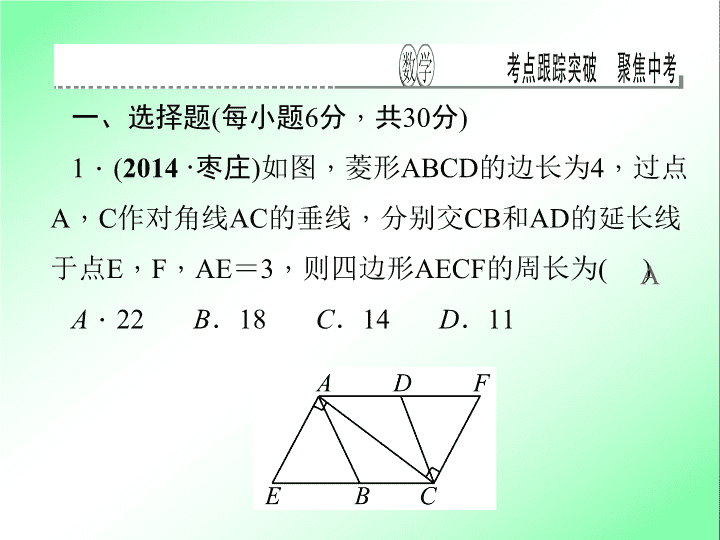
考点跟踪突破 23 　矩形、菱形与正方形 一、选择题 ( 每小题 6 分 ， 共 30 分 ) 1 ． ( 2014 · 枣庄 ) 如图 ， 菱形 ABCD 的边长为 4 ， 过点 A ， C 作对角线 AC 的垂线 ， 分别交 CB 和 AD 的延长线于点 E ， F ， AE ＝ 3 ， 则四边形 AECF 的周长为 ( ) A ． 22 B ． 18 C ． 14 D ． 11 A 2 ． ( 2014 · 丽水 ) 如图， 小红在作线段 AB 的垂直平分线时 ， 是这样操作的：分别以点 A ， B 为圆心 ， 大于线段 AB 长度一半的长为半径画弧 ， 相交于点 C ， D ， 则直线 CD 即为所求．连结 AC ， BC ， AD ， BD ， 根据她的作图方法可知 ， 四边形 ADBC 一定是 ( ) A ． 矩形 B ．菱形 C ． 正方形 D ．等腰梯形 B 3 ． ( 2013· 陕西 ) 如图 ， 在矩形 ABCD 中 ， AD ＝ 2AB ， 点 M ， N 分别在边 AD ， BC 上 ， 连接 BM ， DN ， 若四边形 MBND 是菱形 ， 则 AM MD 等于 ( ) A . 3 8 B . 2 3 C . 3 5 D . 4 5 C 4 ． ( 2014 · 呼和浩特 ) 已知矩形 ABCD 的周长为 20 cm ，两条对角线 AC ， BD 相交于点 O ， 过点 O 作 AC 的垂线 EF ， 分别交两边 AD ， BC 于点 E ， F( 不与顶点重合 ) ， 则以下关于 △ CDE 与 △ ABF 判断完全正确的一项为 ( ) A ． △ CDE 与 △ ABF 的周长都等于 10 cm ， 但面积不一定相等 B ． △ CDE 与 △ ABF 全等 ， 且周长都为 10 cm C ． △ CDE 与 △ ABF 全等 ， 且周长都为 5 cm D ． △ CDE 与 △ ABF 全等 ， 但它们的周长和面积都不能确定 B 5 ． ( 2014· 宜宾 ) 如图 ， 将 n 个边长都为 2 的正方形按如图 所示摆放 ， 点 A 1 ， A 2 ， … A n 分别是正方形的中心 ， 则这 n 个正方形重叠部分的面积之和是 ( ) A ． n B ． n － 1 C ． ( 1 4 ) n － 1 D . 1 4 n B 二、填空题 ( 每小题 6 分 ， 共 30 分 ) 6 ． ( 2014 · 凉山州 ) 顺次连接矩形四边中点所形成的四边形是 ____ ．学校的一块菱形花园两对角线的长分别是 6 m 和 8 m ， 则这个花园的面积为 ____ ． 菱形 24 m 2 7 ． ( 2014 · 毕节 ) 将四根木条钉成的长方形木框变形为平行四边形 ABCD 的形状 ， 并使其面积为长方形面积的一半 ( 木条宽度忽略不计 ) ， 则这个平行四边形的最小内角为 ____ 度． 30 8 ． ( 2014 · 金华 ) 如图 ， 矩形 ABCD 中 ， AB ＝ 8 ， 点 E 是 AD 上的一点 ， 有 AE ＝ 4 ， BE 的垂直平分线交 BC 的延长线于点 F ， 连接 EF 交 CD 于点 G. 若点 G 是 CD 的中点 ， 则 BC 的长是 ____ ． 7 9 ． ( 2013 · 钦州 ) 如图 ， 在正方形 ABCD 中 ， E 是 AB 上一点 ， BE ＝ 2 ， AE ＝ 3BE ， P 是 AC 上一动点 ， 则 PB ＋ PE 的最小值是 ____ ． 10 10 ． 如图 ， 在正方形 ABCD 中 ， 边长为 2 的等边三角形 AEF 的顶点 E ， F 分别在 BC 和 CD 上 ， 下列结论： ① CE ＝ CF ； ②∠ AEB ＝ 75 ° ； ③ BE ＋ DF ＝ EF ； ④ S 正方形 ABCD ＝ 2 ＋ 3 . 其中正确的序号是 ． ( 把你认为正确的 都填上 ) ①②④ 三、解答题 ( 共 40 分 ) 11 ． (10 分 ) ( 2013 · 白银 ) 如图 ， 在 △ ABC 中 ， D 是 BC 边上的一点 ， E 是 AD 的中点 ， 过 A 点作 BC 的平行线交 CE 的延长线于点 F ， 且 AF ＝ BD ， 连接 BF. (1)BD 与 CD 之间有什么数量关系 ， 并说明理由； (2) 当 △ ABC 满足什么条件时 ， 四边形 AFBD 是矩形？并说明理由． (2) 当 △ ABC 满足： AB ＝ AC 时 ， 四边形 AFBD 是矩形．理由如下： ∵ AF ∥ BD ， AF ＝ BD ， ∴ 四边形 AFBD 是平行四边形 ， ∵ AB ＝ AC ， BD ＝ CD ， ∴∠ ADB ＝ 90° ， ∴ ▱ AFBD 是矩形 12 ． (10 分 ) ( 2014 · 临夏州 ) 点 D ， E 分别是不等边三角形 ABC( 即 AB ≠ BC ≠ AC) 的边 AB ， AC 的中点． O 是 △ ABC 所在平面上的动点 ， 连接 OB ， OC ， 点 G ， F 分别是 OB ， OC 的中点 ， 顺次连接点 D ， G ， F ， E. (1) 如图 ， 当点 O 在 △ ABC 的内部时 ， 求证：四边形 DGFE 是平行四边形； (2) 若四边形 DGFE 是菱形 ， 则 OA 与 BC 应满足怎样的数量关系？ ( 直接写出答案 ， 不需要说明理由． ) (2) 解：当 OA ＝ BC 时 ， 平行四边形 DEFG 是菱形 13 ． (10 分 ) ( 2014 · 梅州 ) 如图 ， 在正方形 ABCD 中 ， E 是 AB 上一点 ， F 是 AD 延长线上一点 ， 且 DF ＝ BE. (1) 求证： CE ＝ CF ； (2) 若点 G 在 AD 上 ， 且 ∠ GCE ＝ 45° ， 则 GE ＝ BE ＋ GD 成立吗？为什么？ 解： (1) 证明：在正方形 ABCD 中 ， ∵ BC ＝ CD ， ∠ B ＝ ∠ CDF ， BE ＝ DF ， ∴△ CBE ≌△ CDF( SAS ) ． ∴ CE ＝ CF (2) 解： GE ＝ BE ＋ GD 成立．理由是： ∵ 由 (1) 得 △ CBE ≌△ CDF ， ∴∠ BCE ＝ ∠ DCF ， ∴∠ BCE ＋ ∠ ECD ＝ ∠ DCF ＋ ∠ ECD ， 即 ∠ ECF ＝ ∠ BCD ＝ 90° ， 又 ∵∠ GCE ＝ 45° ， ∴∠ GCF ＝ ∠ GCE ＝ 45°. ∵ CE ＝ CF ， ∠ GCE ＝ ∠ GCF ， GC ＝ GC ， ∴△ ECG ≌△ FCG( SAS ) ． ∴ GE ＝ GF. ∴ GE ＝ DF ＋ GD ＝ BE ＋ GD 14 ． (10 分 ) ( 2013 · 呼和浩特 ) 如图 ， 在边长为 3 的正方形 ABCD 中 ， 点 E 是 BC 边上的点 ， BE ＝ 1 ， ∠ AEP ＝ 90° ， 且 EP 交正方形外角的平分线 CP 于点 P ， 交边 CD 于点 F. ( 1 ) FC EF 的值为 __ __ ； (2) 求证： AE ＝ EP ； (3) 在 AB 边上是否存在点 M ， 使得四边形 DMEP 是平行四边形？若存在 ， 请给予证明；若不存在 ， 请说明理由．