2018年四川省泸州市中考数学试卷含答案 23页

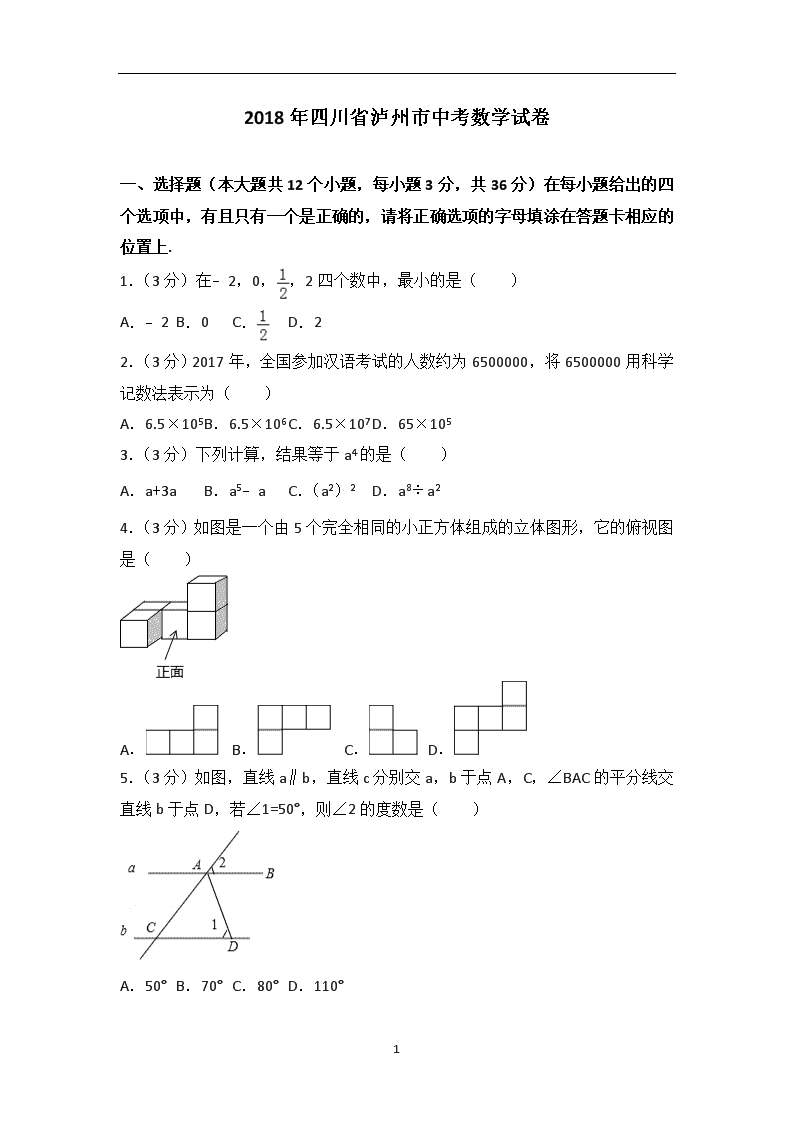
‎2018年四川省泸州市中考数学试卷 ‎　‎ 一、选择题（本大题共12个小题，每小题3分，共36分）在每小题给出的四个选项中，有且只有一个是正确的，请将正确选项的字母填涂在答题卡相应的位置上.‎ ‎1．（3分）在﹣2，0，，2四个数中，最小的是（　　）‎ A．﹣2 B．0 C． D．2‎ ‎2．（3分）2017年，全国参加汉语考试的人数约为6500000，将6500000用科学记数法表示为（　　）‎ A．6.5×105 B．6.5×106 C．6.5×107 D．65×105‎ ‎3．（3分）下列计算，结果等于a4的是（　　）‎ A．a+3a B．a5﹣a C．（a2）2 D．a8÷a2‎ ‎4．（3分）如图是一个由5个完全相同的小正方体组成的立体图形，它的俯视图是（　　）‎ A． B． C． D．‎ ‎5．（3分）如图，直线a∥b，直线c分别交a，b于点A，C，∠BAC的平分线交直线b于点D，若∠1=50°，则∠2的度数是（　　）‎ A．50° B．70° C．80° D．110°‎ 23‎ ‎6．（3分）某校对部分参加夏令营的中学生的年龄（单位：岁）进行统计，结果如下表：‎ 年龄 ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ 人数 ‎1‎ ‎2‎ ‎2‎ ‎3‎ ‎1‎ 则这些学生年龄的众数和中位数分别是（　　）‎ A．16，15 B．16，14 C．15，15 D．14，15‎ ‎7．（3分）如图，▱ABCD的对角线AC，BD相交于点O，E是AB中点，且AE+EO=4，则▱ABCD的周长为（　　）‎ A．20 B．16 C．12 D．8‎ ‎8．（3分）“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则小正方形的边长为（　　）‎ A．9 B．6 C．4 D．3‎ ‎9．（3分）已知关于x的一元二次方程x2﹣2x+k﹣1=0有两个不相等的实数根，则实数k的取值范围是（　　）‎ A．k≤2 B．k≤0 C．k＜2 D．k＜0‎ ‎10．（3分）如图，正方形ABCD中，E，F分别在边AD，CD上，AF，BE相交于点G，若AE=3ED，DF=CF，则的值是（　　）‎ 23‎ A． B． C． D．‎ ‎11．（3分）在平面直角坐标系内，以原点O为原心，1为半径作圆，点P在直线y=上运动，过点P作该圆的一条切线，切点为A，则PA的最小值为（　　）‎ A．3 B．2 C． D．‎ ‎12．（3分）已知二次函数y=ax2+2ax+3a2+3（其中x是自变量），当x≥2时，y随x的增大而增大，且﹣2≤x≤1时，y的最大值为9，则a的值为（　　）‎ A．1或﹣2 B．或 C． D．1‎ ‎　‎ 二、填空题（每小题3分，共12分）‎ ‎13．（3分）若二次根式在实数范围内有意义，则x的取值范围是　 　．‎ ‎14．（3分）分解因式：3a2﹣3=　 　．‎ ‎15．（3分）已知x1，x2是一元二次方程x2﹣2x﹣1=0的两实数根，则的值是　 　．‎ ‎16．（3分）如图，等腰△ABC的底边BC=20，面积为120，点F在边BC上，且BF=3FC，EG是腰AC的垂直平分线，若点D在EG上运动，则△CDF周长的最小值为　 　．‎ ‎　‎ 23‎ 三、（每小题6分，共18分）‎ ‎17．（6分）计算：π0++（）﹣1﹣|﹣4|．‎ ‎18．（6分）如图，EF=BC，DF=AC，DA=EB．求证：∠F=∠C．‎ ‎19．（6分）化简：（1+）÷．‎ ‎　‎ 四、（每小题7分，共14分）‎ ‎20．（7分）为了解某中学学生课余生活情况，对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计．现从该校随机抽取n名学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名学生只能选择其中一项）．并根据调查得到的数据绘制成了如图7所示的两幅不完整的统计图．由图中提供的信息，解答下列问题：‎ ‎（1）求n的值；‎ ‎（2）若该校学生共有1200人，试估计该校喜爱看电视的学生人数；‎ ‎（3）若调查到喜爱体育活动的4名学生中有3名男生和1名女生，现从这4名学生中任意抽取2名学生，求恰好抽到2名男生的概率．‎ ‎21．（7分）某图书馆计划选购甲、乙两种图书．已知甲图书每本价格是乙图书每本价格的2.5倍，用800元单独购买甲图书比用800元单独购买乙图书要少24本．‎ ‎（1）甲、乙两种图书每本价格分别为多少元？‎ 23‎ ‎（2）如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本，且用于购买甲、乙两种图书的总经费不超过1060元，那么该图书馆最多可以购买多少本乙图书？‎ ‎　‎ 五、（每小题8分，共16分）‎ ‎22．（8分）如图，甲建筑物AD，乙建筑物BC的水平距离AB为90m，且乙建筑物的高度是甲建筑物高度的6倍，从E（A，E，B在同一水平线上）点测得D点的仰角为30°，测得C点的仰角为60°，求这两座建筑物顶端C、D间的距离（计算结果用根号表示，不取近似值）．‎ ‎23．（8分）一次函数y=kx+b的图象经过点A（﹣2，12），B（8，﹣3）．‎ ‎（1）求该一次函数的解析式；‎ ‎（2）如图，该一次函数的图象与反比例函数y=（m＞0）的图象相交于点C（x1，y1），D（x2，y2），与y轴交于点E，且CD=CE，求m的值．‎ ‎　‎ 六、（每小题12分，共24分）‎ ‎24．（12分）如图，已知AB，CD是⊙O的直径，过点C作⊙O的切线交AB的延长线于点P，⊙O的弦DE交AB于点F，且DF=EF．‎ 23‎ ‎（1）求证：CO2=OF•OP；‎ ‎（2）连接EB交CD于点G，过点G作GH⊥AB于点H，若PC=4，PB=4，求GH的长．‎ ‎25．（12分）如图11，已知二次函数y=ax2﹣（2a﹣）x+3的图象经过点A（4，0），与y轴交于点B．在x轴上有一动点C（m，0）（0＜m＜4），过点C作x轴的垂线交直线AB于点E，交该二次函数图象于点D．‎ ‎（1）求a的值和直线AB的解析式；‎ ‎（2）过点D作DF⊥AB于点F，设△ACE，△DEF的面积分别为S1，S2，若S1=4S2，求m的值；‎ ‎（3）点H是该二次函数图象上位于第一象限的动点，点G是线段AB上的动点，当四边形DEGH是平行四边形，且▱DEGH周长取最大值时，求点G的坐标．‎ ‎　‎ 23‎ ‎2018年四川省泸州市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12个小题，每小题3分，共36分）在每小题给出的四个选项中，有且只有一个是正确的，请将正确选项的字母填涂在答题卡相应的位置上.‎ ‎1．（3分）在﹣2，0，，2四个数中，最小的是（　　）‎ A．﹣2 B．0 C． D．2‎ ‎【解答】解：由正数大于零，零大于负数，得 ‎﹣2＜0＜＜2，‎ ‎﹣2最小，‎ 故选：A．‎ ‎　‎ ‎2．（3分）2017年，全国参加汉语考试的人数约为6500000，将6500000用科学记数法表示为（　　）‎ A．6.5×105 B．6.5×106 C．6.5×107 D．65×105‎ ‎【解答】解：6500000=6.5×106，‎ 故选：B．‎ ‎　‎ ‎3．（3分）下列计算，结果等于a4的是（　　）‎ A．a+3a B．a5﹣a C．（a2）2 D．a8÷a2‎ ‎【解答】解：A、a+3a=4a，错误；‎ B、a5和a不是同类项，不能合并，故此选项错误；‎ C、（a2）2=a4，正确；‎ D、a8÷a2=a6，错误；‎ 故选：C．‎ ‎　‎ 23‎ ‎4．（3分）如图是一个由5个完全相同的小正方体组成的立体图形，它的俯视图是（　　）‎ A． B． C． D．‎ ‎【解答】解：从上面看第一列是两个小正方形，第二列是一个小正方形，第三列是一个小正方形，‎ 故选：B．‎ ‎　‎ ‎5．（3分）如图，直线a∥b，直线c分别交a，b于点A，C，∠BAC的平分线交直线b于点D，若∠1=50°，则∠2的度数是（　　）‎ A．50° B．70° C．80° D．110°‎ ‎【解答】解：∵∠BAC的平分线交直线b于点D，‎ ‎∴∠BAD=∠CAD，‎ ‎∵直线a∥b，∠1=50°，‎ ‎∴∠BAD=∠CAD=50°，‎ ‎∴∠2=180°﹣50°﹣50°=80°．‎ 故选：C．‎ ‎　‎ ‎6．（3分）某校对部分参加夏令营的中学生的年龄（单位：岁）进行统计，结果如下表：‎ 23‎ 年龄 ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ 人数 ‎1‎ ‎2‎ ‎2‎ ‎3‎ ‎1‎ 则这些学生年龄的众数和中位数分别是（　　）‎ A．16，15 B．16，14 C．15，15 D．14，15‎ ‎【解答】解：由表可知16岁出现次数最多，所以众数为16岁，‎ 因为共有1+2+2+3+1=9个数据，‎ 所以中位数为第5个数据，即中位数为15岁，‎ 故选：A．‎ ‎　‎ ‎7．（3分）如图，▱ABCD的对角线AC，BD相交于点O，E是AB中点，且AE+EO=4，则▱ABCD的周长为（　　）‎ A．20 B．16 C．12 D．8‎ ‎【解答】解：∵四边形ABCD是平行四边形，‎ ‎∴OA=OC，‎ ‎∵AE=EB，‎ ‎∴OE=BC，‎ ‎∵AE+EO=4，‎ ‎∴2AE+2EO=8，‎ ‎∴AB+BC=8，‎ ‎∴平行四边形ABCD的周长=2×8=16，‎ 故选：B．‎ ‎　‎ ‎8．（3分）“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则小正方形的边长为（　　）‎ 23‎ A．9 B．6 C．4 D．3‎ ‎【解答】解：由题意可知：中间小正方形的边长为：a﹣b，‎ ‎∵每一个直角三角形的面积为：ab=×8=4，‎ ‎∴4×ab+（a﹣b）2=25，‎ ‎∴（a﹣b）2=25﹣16=9，‎ ‎∴a﹣b=3，‎ 故选：D．‎ ‎　‎ ‎9．（3分）已知关于x的一元二次方程x2﹣2x+k﹣1=0有两个不相等的实数根，则实数k的取值范围是（　　）‎ A．k≤2 B．k≤0 C．k＜2 D．k＜0‎ ‎【解答】解：根据题意得△=（﹣2）2﹣4（k﹣1）＞0，‎ 解得k＜2．‎ 故选：C．‎ ‎　‎ ‎10．（3分）如图，正方形ABCD中，E，F分别在边AD，CD上，AF，BE相交于点G，若AE=3ED，DF=CF，则的值是（　　）‎ A． B． C． D．‎ ‎【解答】解：如图作，FN∥AD，交AB于N，交BE于M．‎ 23‎ ‎∵四边形ABCD是正方形，‎ ‎∴AB∥CD，∵FN∥AD，‎ ‎∴四边形ANFD是平行四边形，‎ ‎∵∠D=90°，‎ ‎∴四边形ANFD是解析式，‎ ‎∵AE=3DE，设DE=a，则AE=3a，AD=AB=CD=FN=4a，AN=DF=2a，‎ ‎∵AN=BN，MN∥AE，‎ ‎∴BM=ME，‎ ‎∴MN=a，‎ ‎∴FM=a，‎ ‎∵AE∥FM，‎ ‎∴===，‎ 故选：C．‎ ‎　‎ ‎11．（3分）在平面直角坐标系内，以原点O为原心，1为半径作圆，点P在直线y=上运动，过点P作该圆的一条切线，切点为A，则PA的最小值为（　　）‎ A．3 B．2 C． D．‎ ‎【解答】解：如图，直线y=x+2与x轴交于点C，与y轴交于点D，作OH⊥CD于H，‎ 当x=0时，y=x+2=2，则D（0，2），‎ 当y=0时，x+2=0，解得x=﹣2，则C（﹣2，0），‎ ‎∴CD==4，‎ 23‎ ‎∵OH•CD=OC•OD，‎ ‎∴OH==，‎ 连接OA，如图，‎ ‎∵PA为⊙O的切线，‎ ‎∴OA⊥PA，‎ ‎∴PA==，‎ 当OP的值最小时，PA的值最小，‎ 而OP的最小值为OH的长，‎ ‎∴PA的最小值为=．‎ 故选：D．‎ ‎　‎ ‎12．（3分）已知二次函数y=ax2+2ax+3a2+3（其中x是自变量），当x≥2时，y随x的增大而增大，且﹣2≤x≤1时，y的最大值为9，则a的值为（　　）‎ A．1或﹣2 B．或 C． D．1‎ ‎【解答】解：∵二次函数y=ax2+2ax+3a2+3（其中x是自变量），‎ ‎∴对称轴是直线x=﹣=﹣1，‎ ‎∵当x≥2时，y随x的增大而增大，‎ ‎∴a＞0，‎ ‎∵﹣2≤x≤1时，y的最大值为9，‎ ‎∴x=1时，y=a+2a+3a2+3=9，‎ ‎∴3a2+3a﹣6=0，‎ 23‎ ‎∴a=1，或a=﹣2（不合题意舍去）．‎ 故选：D．‎ ‎　‎ 二、填空题（每小题3分，共12分）‎ ‎13．（3分）若二次根式在实数范围内有意义，则x的取值范围是　x≥1　．‎ ‎【解答】解：∵式子在实数范围内有意义，‎ ‎∴x﹣1≥0，‎ 解得x≥1．‎ 故答案为：x≥1．‎ ‎　‎ ‎14．（3分）分解因式：3a2﹣3=　3（a+1）（a﹣1）　．‎ ‎【解答】解：3a2﹣3，‎ ‎=3（a2﹣1），‎ ‎=3（a+1）（a﹣1）．‎ 故答案为：3（a+1）（a﹣1）．‎ ‎　‎ ‎15．（3分）已知x1，x2是一元二次方程x2﹣2x﹣1=0的两实数根，则的值是　6　．‎ ‎【解答】解：∵x1、x2是一元二次方程x2﹣2x﹣1=0的两实数根，‎ ‎∴x1+x2=2，x1x2=﹣1，=2x1+1，=2x2+1，‎ ‎∴=+====6．‎ 故答案为：6．‎ ‎　‎ ‎16．（3分）如图，等腰△‎ 23‎ ABC的底边BC=20，面积为120，点F在边BC上，且BF=3FC，EG是腰AC的垂直平分线，若点D在EG上运动，则△CDF周长的最小值为　13　．‎ ‎【解答】解：如图作AH⊥BC于H，连接AD．‎ ‎∵EG垂直平分线段AC，‎ ‎∴DA=DC，‎ ‎∴DF+DC=AD+DF，‎ ‎∴当A、D、F共线时，DF+DC的值最小，最小值就是线段AF的长，‎ ‎∵•BC•AH=120，‎ ‎∴AH=12，‎ ‎∵AB=AC，AH⊥BC，‎ ‎∴BH=CH=10，‎ ‎∵BF=3FC，‎ ‎∴CF=FH=5，‎ ‎∴AF===13，‎ ‎∴DF+DC的最小值为13．‎ 故答案为13．‎ ‎　‎ 三、（每小题6分，共18分）‎ ‎17．（6分）计算：π0++（）﹣1﹣|﹣4|．‎ ‎【解答】解：原式=1+4+2﹣4=3．‎ 23‎ ‎　‎ ‎18．（6分）如图，EF=BC，DF=AC，DA=EB．求证：∠F=∠C．‎ ‎【解答】证明：∵DA=BE，‎ ‎∴DE=AB，‎ 在△ABC和△DEF中，‎ ‎，‎ ‎∴△ABC≌△DEF（SSS），‎ ‎∴∠C=∠F．‎ ‎　‎ ‎19．（6分）化简：（1+）÷．‎ ‎【解答】解：原式=•‎ ‎=．‎ ‎　‎ 四、（每小题7分，共14分）‎ ‎20．（7分）为了解某中学学生课余生活情况，对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计．现从该校随机抽取n名学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名学生只能选择其中一项）．并根据调查得到的数据绘制成了如图7所示的两幅不完整的统计图．由图中提供的信息，解答下列问题：‎ ‎（1）求n的值；‎ ‎（2）若该校学生共有1200人，试估计该校喜爱看电视的学生人数；‎ ‎（3）若调查到喜爱体育活动的4名学生中有3名男生和1名女生，现从这4名学生中任意抽取2名学生，求恰好抽到2名男生的概率．‎ 23‎ ‎【解答】解：（1）n=5÷10%=50；‎ ‎（2）样本中喜爱看电视的人数为50﹣15﹣20﹣5=10（人），‎ ‎1200×=240，‎ 所以估计该校喜爱看电视的学生人数为240人；‎ ‎（3）画树状图为：‎ 共有12种等可能的结果数，其中恰好抽到2名男生的结果数为6，‎ 所以恰好抽到2名男生的概率==．‎ ‎　‎ ‎21．（7分）某图书馆计划选购甲、乙两种图书．已知甲图书每本价格是乙图书每本价格的2.5倍，用800元单独购买甲图书比用800元单独购买乙图书要少24本．‎ ‎（1）甲、乙两种图书每本价格分别为多少元？‎ ‎（2）如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本，且用于购买甲、乙两种图书的总经费不超过1060元，那么该图书馆最多可以购买多少本乙图书？‎ ‎【解答】解：（1）设乙图书每本价格为x元，则甲图书每本价格是2.5x元，‎ 根据题意可得：﹣=24，‎ 解得：x=20，‎ 经检验得：x=20是原方程的根，‎ 则2.5x=50，‎ 23‎ 答：乙图书每本价格为20元，则甲图书每本价格是50元；‎ ‎（2）设购买甲图书本数为x，则购买乙图书的本数为：2x+8，‎ 故50x+20（2x+8）≤1060，‎ 解得：x≤10，‎ 故2x+8≤28，‎ 答：该图书馆最多可以购买28本乙图书．‎ ‎　‎ 五、（每小题8分，共16分）‎ ‎22．（8分）如图，甲建筑物AD，乙建筑物BC的水平距离AB为90m，且乙建筑物的高度是甲建筑物高度的6倍，从E（A，E，B在同一水平线上）点测得D点的仰角为30°，测得C点的仰角为60°，求这两座建筑物顶端C、D间的距离（计算结果用根号表示，不取近似值）．‎ ‎【解答】解：由题意知：BC=6AD，AE+BE=AB=90m 在Rt△ADE中，tan30°=，sin30°=‎ ‎∴AE==AD，DE=2AD；‎ 在Rt△BCE中，tan60°=，sin60°=，‎ ‎∴BE==2AD，CE==4AD；‎ ‎∵AE+BE=AB=90m ‎∴AD+2AD=90‎ ‎∴AD=10（m）‎ 23‎ ‎∴DE=20m，CE=120m ‎∵∠DEA+∠DEC+∠CEB=180°，∠DEA=30°，∠CEB=60°，‎ ‎∴∠DEC=90°‎ ‎∴CD===20（m）‎ 答：这两座建筑物顶端C、D间的距离为20m．‎ ‎　‎ ‎23．（8分）一次函数y=kx+b的图象经过点A（﹣2，12），B（8，﹣3）．‎ ‎（1）求该一次函数的解析式；‎ ‎（2）如图，该一次函数的图象与反比例函数y=（m＞0）的图象相交于点C（x1，y1），D（x2，y2），与y轴交于点E，且CD=CE，求m的值．‎ ‎【解答】解：（1）把点A（﹣2，12），B（8，﹣3）代入y=kx+b 得：‎ 解得：‎ ‎∴一次函数解析式为：y=﹣‎ ‎（2）分别过点C、D做CA⊥y轴于点A，DB⊥y轴于点B 23‎ 设点C坐标为（a，b），由已知ab=m 由（1）点E坐标为（0，9），则AE=9﹣b ‎∵AC∥BD，CD=CE ‎∴BD=2a，EB=2（9﹣b）‎ ‎∴OB=9﹣2（9﹣b）=2b﹣9‎ ‎∴点D坐标为（2a，2b﹣9）‎ ‎∴2a•（2b﹣9）=m 整理得m=6a ‎∵ab=m ‎∴b=6‎ 则点D坐标化为（a，3）‎ ‎∵点D在y=﹣图象上 ‎∴a=4‎ ‎∴m=ab=24‎ ‎　‎ 六、（每小题12分，共24分）‎ ‎24．（12分）如图，已知AB，CD是⊙O的直径，过点C作⊙O的切线交AB的延长线于点P，⊙O的弦DE交AB于点F，且DF=EF．‎ ‎（1）求证：CO2=OF•OP；‎ ‎（2）连接EB交CD于点G，过点G作GH⊥AB于点H，若PC=4，PB=4，求GH的长．‎ 23‎ ‎【解答】（1）证明：∵PC是⊙O的切线，‎ ‎∴OC⊥PC，‎ ‎∴∠PCO=90°，‎ ‎∵AB是直径，EF=FD，‎ ‎∴AB⊥ED，‎ ‎∴∠OFD=∠OCP=90°，‎ ‎∵∠FOD=∠COP，‎ ‎∴△OFD∽△OCP，‎ ‎∴=，∵OD=OC，‎ ‎∴OC2=OF•OP．‎ ‎（2）解：如图作CM⊥OP于M，连接EC、EO．设OC=OB=r．‎ 在Rt△POC中，∵PC2+OC2=PO2，‎ ‎∴（4）2+r2=（r+4）2，‎ ‎∴r=2，‎ ‎∵CM==，‎ ‎∵DC是直径，‎ ‎∴∠CEF=∠EFM=∠CMF=90°，‎ 23‎ ‎∴四边形EFMC是矩形，‎ ‎∴EF=CM=，‎ 在Rt△OEF中，OF==，‎ ‎∴EC=2OF=，‎ ‎∵EC∥OB，‎ ‎∴==，‎ ‎∵GH∥CM，‎ ‎∴==，‎ ‎∴GH=．‎ ‎　‎ ‎25．（12分）如图11，已知二次函数y=ax2﹣（2a﹣）x+3的图象经过点A（4，0），与y轴交于点B．在x轴上有一动点C（m，0）（0＜m＜4），过点C作x轴的垂线交直线AB于点E，交该二次函数图象于点D．‎ ‎（1）求a的值和直线AB的解析式；‎ ‎（2）过点D作DF⊥AB于点F，设△ACE，△DEF的面积分别为S1，S2，若S1=4S2，求m的值；‎ ‎（3）点H是该二次函数图象上位于第一象限的动点，点G是线段AB上的动点，当四边形DEGH是平行四边形，且▱DEGH周长取最大值时，求点G的坐标．‎ ‎【解答】解：（1）把点A（4，0）代入，得 ‎0=a•42﹣（2a﹣）×4+3‎ 23‎ 解得 a=﹣‎ ‎∴函数解析式为：y=‎ 设直线AB解析式为y=kx+b 把A（4，0），B（0，3）代入 解得 ‎∴直线AB解析式为：y=﹣‎ ‎（2）由已知，‎ 点D坐标为（m，﹣）‎ 点E坐标为（m，﹣）‎ ‎∴AC=4﹣m DE=（﹣）﹣（﹣）=﹣‎ ‎∵BC∥y轴 ‎∴‎ ‎∴AE=‎ ‎∵∠DFA=∠DCA=90°，∠FBD=∠CEA ‎∴△DEF∽△AEC ‎∵S1=4S2‎ ‎∴AE=2DE ‎∴‎ 解得m1=，m2=﹣（舍去）‎ 故m值为 ‎（3）如图，过点G做GM⊥DC于点M 23‎ 由（2）DE=﹣‎ 同理HG=﹣‎ ‎∵四边形DEGH是平行四边形 ‎∴﹣=﹣‎ 整理得：（n﹣m）[]=0‎ ‎∵m≠n ‎∴m+n=4，即n=4﹣m ‎∴MG=n﹣m=4﹣2m 由已知△EMG∽△BOA ‎∴‎ ‎∴EG=‎ ‎∴▱DEGH周长L=2[﹣+]=﹣‎ ‎∵a=﹣＜0‎ ‎∴m=﹣时，L最大．‎ ‎∴n=4﹣=‎ ‎∴G点坐标为（，）‎ ‎　‎ 23‎