中考九年级数学学练测91圆的有关性质 50页

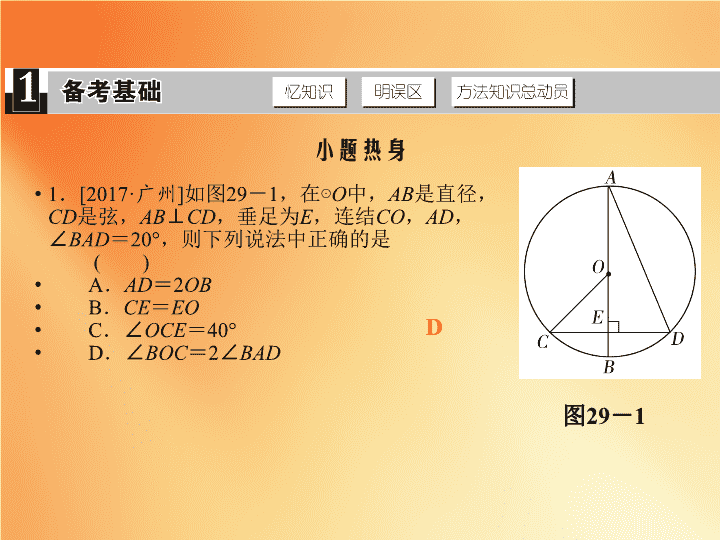
第九单元 圆 圆的有关性质 1 ． [2017· 广州 ] 如图 29 － 1 ，在 ⊙ O 中， AB 是直径， CD 是弦， AB ⊥ CD ，垂足为 E ，连结 CO ， AD ，∠ BAD ＝ 20° ，则下列说法中正确的是 ( 　　 ) A ． AD ＝ 2 OB B ． CE ＝ EO C ．∠ OCE ＝ 40° D ．∠ BOC ＝ 2∠ BAD 小题热身 D 图 29 － 1 2 ．在圆内接四边形 ABCD 中，已知 ∠ A ＝ 70° ，则 ∠ C ＝ ( 　　 ) A ． 20° B ． 30° C ． 70° D ． 110° D 3 ． [2017· 眉山 ] 如图 29 － 2 ， AB 是 ⊙ O 的弦，半径 OC ⊥ AB 于点 D ，且 AB ＝ 8 cm ， DC ＝ 2 cm ，则 OC ＝ ___cm. 图 29 － 2 5 第 3 题答图 4 ． [2017· 重庆 A 卷 ] 如图 29 － 3 ， BC 是 ⊙ O 的直径，点 A 在圆上，连结 AO ， AC ，∠ AOB ＝ 64° ，则 ∠ ACB ＝ ____ ． 【 解析 】 ∵ AO ＝ OC ，∴∠ ACB ＝ ∠ OAC ，∵∠ AOB ＝ 64° ，∴∠ ACB ＋∠ OAC ＝ 64° ，∴∠ ACB ＝ 64°÷2 ＝ 32°. 图 29 － 3 32 ° 一、必知 8 知识点 1 ． 圆的有关概念 定义：在同一平面内，线段 OP 绕它固定的一个端点 O 旋转一周，另一个端点 P 所经过的封闭曲线叫做圆，定点 O 叫做 _____ ，线段 OP 叫做 __________ ． 圆的集合定义：圆是到定点的距离等于 _____ 的点的集合． 考点管理 圆心 圆的半径 定长 圆的有关概念：连结圆上任意两点的线段叫做 ____ ；经过圆心的弦叫做 _____ ；圆上任意两点间的部分叫做 ____ ；大于半圆的弧叫做 _____ ；小于半圆的弧叫做 _____ ；圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做 ____ ． 2 ． 点和圆的位置关系 如果圆的半径是 r ，点到圆心的距离为 d ，那么： (1) 点在圆外 ⇔____ ； (2) 点在圆上 ⇔_____ ； (3) 点在圆内 ⇔____ ． 弦 直径 弧 优弧 劣弧 半圆 d > r d ＝ r d < r 3 ． 确定圆的条件 确定圆的条件：不在同一条直线上的三个点确定 ____ 个圆． 三角形的外接圆：经过三角形各个顶点的圆； 三角形外接圆的圆心叫做三角形的外心，三角形叫做圆的内接三角形． 一 【 智慧锦囊 】 三角形的外心是三角形三边垂直平分线的交点，锐角三角形的外心在三角形的 _____ ，直角三角形的外心是 _______________ _______ ，钝角三角形的外心在三角形的 _____ ． 内部 直角三角形斜边 外部 的中点 4 ． 圆的对称性 圆既是一个轴对称图形又是一个 _____ 对称图形，圆还具有旋转不变性． 5 ． 垂径定理及其推论 垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的 ____ ． 推论： (1) 平分弦 ( 非直径 ) 的直径垂直于弦，并且平分弦所对的两条弧； (2) 平分弧的直径垂直平分弧所对的弦． 中心 弧 【 智慧锦囊 】 用垂径定理进行计算或证明时，常常连结半径或作出弦心距，构造出直角三角形求解 ． 6 ． 圆心角、弧、弦、弦心距之间的关系 圆心角定理：在同圆或等圆中，相等的圆心角所对的弧 _____ ，所对的弦 _____ ． 推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等，那么它们所对应的其余各对量都相等． 7 ． 圆周角 圆周角：顶点在圆上，它的两边都和圆相交的角； 圆周角定理：圆周角的度数等于它所对的弧上圆心角度数的 _____ ． 相等 相等 一半 推论： (1) 半圆 ( 或直径 ) 所对的圆周角是 ____ 角； (2)90° 的圆周角所对的弦是 _____ ； (3) 在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧 _____ ． 8 ． 圆内接四边形 圆内接四边形：如果一个四边形的各个顶点在同一个圆上，那么这个四边形叫做圆内接四边形，这个圆叫做四边形的外接圆． 性质：圆内接四边形的对角互补． 直 直径 相等 二、必会 2 方法 1 ． 添加辅助线 (1) 有关弦的问题，常作其弦心距，构造直角三角形，如图 29 － 4 ； (2) 有关直径的问题，常作直径所对的圆周角，如图 29 － 5. 图 29 － 4 图 29 － 5 2 ． 分类讨论 在圆中，常涉及到分类讨论，如一条弦所对的弧有优弧和劣弧两种，则其所对的圆周角不一定相等；另外，有关于弦的问题也需要分类讨论，如有两条弦时，需要分在圆心同侧还是异侧等．此类问题是中考的热点． 点与圆的位置关系 [2018· 中考预测 ] 如图 29 － 6 ，在 Rt △ ABC 中，∠ ACB ＝ 90° ， AC ＝ 3 ， BC ＝ 4 ， CP ， CM 分别是 AB 上的高线和中线， 如果 ⊙ A 是以点 A 为圆心，半径长为 2 的圆， 那么下列判断正确的是 ( 　　 ) C 图 29 － 6 A ．点 P ， M 均在 ⊙ A 内 B ．点 P ， M 均在 ⊙ A 外 C ．点 P 在 ⊙ A 内，点 M 在 ⊙ A 外 D ．点 P 在 ⊙ A 外，点 M 在 ⊙ A 内 【 点悟 】 　点与圆的位置关系的判定，根据点与圆心之间的距离和圆的半径的大小作出判断． [2017· 枣庄 ] 如图 29 － 7 ，在网格 ( 每个小正方形的边长均为 1) 中选取 9 个格点 ( 格线的交点称为格点 ) ．如果以 A 为圆心， r 为半径画圆，选取的格点中除点 A 外恰好有 3 个在圆内，则 r 的取值范围为 ( 　　 ) B 图 29 － 7 变式跟进答图 圆心角、弧、弦之间的关系 [2016· 舟山 ] 把一张圆形纸片按如图 29 － 8 的方式折叠两次后展开 ( 图中的虚线表示折痕 ) ，则的度数是 ( 　　 ) A ． 120 ° B ． 135 ° C ． 150 ° D ． 165 ° 图 29 － 8 C 例 2 答图 【 点悟 】 　 (1) 在同圆 ( 或等圆 ) 中，圆心角 ( 或圆周角 ) 、弧、弦、弦心距中只要有一组量相等，则其他对应的各组量也分别相等．利用这个性质可以将问题互相转化，达到求解或证明的目的； (2) 注意圆中的隐含条件：半径相等； (3) 注意分类讨论思想的应用． 1 ．如图 29 － 9 ，圆心角 ∠ AOB ＝ 20° ，将旋转 n ° 得到，则的度数是 _____ 度． 20 图 29 － 9 2 ．如图 29 － 10 ， A ， B 是 ⊙ O 上的两点，∠ AOB ＝ 120° ， C 是的中点． (1) 求证： AB 平分 ∠ OAC ； (2) 延长 OA 至点 P 使得 OA ＝ AP ，连结 PC ，若 ⊙ O 的半径 R ＝ 1 ，求 PC 的长． 图 29 － 10 变式跟进 2 答 图 【 解析 】 (1) 证得等边三角形 AOC 和等边三角形 OBC ，推出 OA ＝ OB ＝ BC ＝ AC ； (2) 求出 AC ＝ OA ＝ AP ，∠ PCO ＝ 90° ，∠ P ＝ 30°. 解 ： (1) 证明：如答图，连结 OC . ∵∠ AOB ＝ 120° ， C 是的中点， ∴∠ AOC ＝ ∠ BOC ＝ 60° ， ∵ OA ＝ OC ，∴△ ACO 是等边三角形， ∴ OA ＝ AC . 同理， OB ＝ BC ， ∴ OA ＝ AC ＝ BC ＝ OB . ∴四边形 AOBC 是菱形， ∴ AB 平分 ∠ OAC ； (2) 由 (1) 知 OA ＝ AC ，又 ∵ OA ＝ AP ，∴ AP ＝ AC ， ∵∠ PAC ＝ 180° － ∠ OAC ＝ 120° ， ∴∠ P ＝ ∠ ACP ＝ 30° ，∴∠ PCO ＝ 90° ， 垂径定理及其推论 [2017· 金华 ] 如图 29 － 11 ，在半径为 13 cm 的圆形铁片上切下一块高为 8 cm 的弓形铁片，则弓形弦 AB 的长为 ( 　　 ) A ． 10 cm B ． 16 cm C ． 24 cm D ． 26 cm C 图 29 － 11 1 ．一条排水管的截面如图 29 － 12 所示，已知 排水管的半径 OA ＝ 1 m ，水面宽 AB ＝ 1.2 m ， 某天下雨后，水管水面上升了 0.2 m ，则此时 排水管水面宽 CD 等于 ____m. 【 解析 】 如答图，连结 OC ，作 OE ⊥ AB ， 垂足为 E ，与 CD 交于 F 点， OA ＝ 1 m ， EA ＝ 0.6 m ， 根据勾股定理，得 OE ＝ 0.8 m ， EF ＝ 0.2 m ， 则 OF ＝ 0.6 m ，在 △ OCF 中， OF ＝ 0.6 m ， OC ＝ 1 m ，得 CF ＝ 0.8 m ，∴ CD ＝ 1.6 m ，故答案为 1.6 m. 图 29 － 12 变式跟进 1 答图 1.6 2 ．赵州桥是我国建筑史上的一大创举，它距今约 1 400 年，历经无数次洪水冲击和多次地震却安然无恙．如图 29 － 13 ，若桥跨度 AB 约为 40 m ，主拱高 CD 约 10 m ，则桥弧 AB 所在圆的半径 R ＝ ______m. 25 图 29 － 13 3 ． [2016· 绍兴 ] 如图 29 － 14① ，小敏利用课余时间制作了一个脸盆架，如图 ② 是它的截面图，垂直放置的脸盆与架子的交点为 A ， B ， AB ＝ 40 cm ，脸盆的最低点 C 到 AB 的距离为 10 cm ，则该脸盆的半径为 ______cm. 25 图 29 － 14 【 解析 】 如答图，设圆的圆心为 O ，连结 OA ， OC ， OC 与 AB 交于点 D ，设 ⊙ O 半径为 R ，在 Rt △ AOD 中利用勾股定理即可解决问题． 如答图，设圆的圆心为 O ，连结 OA ， OC ， OC 与 AB 交于点 D ，设 ⊙ O 半径为 R ， 在 Rt △ AOD 中，∵∠ ADO ＝ 90° ， ∴ OA 2 ＝ OD 2 ＋ AD 2 ， ∴ R 2 ＝ 20 2 ＋ ( R － 10) 2 ， 解得 R ＝ 25 ，脸盆的半径为 25 cm. 变式跟进 3 答图 【 点悟 】 　在已知直径与弦垂直的问题中，常连结半径构造直角三角形，其中斜边为圆的半径，两直角边是弦长的一半和圆心到弦的距离，进而运用勾股定理来计算． 圆周角定理及其推论 [2017· 台州 ] 如图 29 － 15 ，已知等腰直 角三角形 ABC ，点 P 是斜边 BC 上一点 ( 不 与 B ， C 重合 ) ， PE 是 △ ABP 的外接圆 ⊙ O 的直径． (1) 求证： △ APE 是等腰直角三角形； (2) 若 ⊙ O 的直径为 2 ，求 PC 2 ＋ PB 2 的值． 图 29 － 15 解 ： (1) 证明： ∵ AB ＝ AC ，∠ BAC ＝ 90° ， ∴∠ C ＝ ∠ ABC ＝ 45° ， ∴∠ AEP ＝ ∠ ABP ＝ 45° ， ∵ PE 是直径，∴∠ PAE ＝ 90° ， ∴∠ APE ＝ ∠ AEP ＝ 45° ， ∴ AP ＝ AE ，∴△ APE 是等腰直角三角形； (2)∵∠ PAB ＋ ∠ BAE ＝ ∠ PAE ＝ 90° ， ∠ PAB ＋ ∠ CAP ＝ ∠ CAB ＝ 90° ， ∴∠ BAE ＝ ∠ CAP ， ∴△ BAE ≌△ CAP ( SAS ) ，∴ PC ＝ EB ，∵ PE 为 ⊙ O 直径，∴∠ PBE ＝ 90° ， ∴ PE 2 ＝ PB 2 ＋ BE 2 ， ∴ PC 2 ＋ PB 2 ＝ PE 2 ＝ 4. 1 ． [2017· 绍兴 ] 如图 29 － 16 ，一块含 45° 角的 直角三角板，它的一个锐角顶点 A 在 ⊙ O 上，边 AB ， AC 分别与 ⊙ O 交于点 D ， E ， 则 ∠ DOE 的度数为 ______ ． 图 29 － 16 90 ° 2 ．如图 29 － 17 ，⊙ O 的半径为 1 ， A ， P ， B ， C 是 ⊙ O 上的四个点，∠ APC ＝ ∠ CPB ＝ 60°. (1) 判断 △ ABC 的形状，并说明理由； (2) 试探究线段 PA ， PB ， PC 之间的数量关系，并证明你的结论． 图 29 － 17 备用图 【 解析 】 (1) 利用圆周角定理，可得 ∠ BAC ＝ ∠ CPB ，∠ ABC ＝ ∠ APC ，而 ∠ APC ＝ ∠ CPB ＝ 60° ，∴∠ BAC ＝ ∠ ABC ＝ 60° ，从而可判断 △ ABC 的形状； (2) 如答图，在 PC 上截取 PD ＝ AP ，则 △ APD 是等边三角形，然后证明 △ APB ≌△ ADC ，得出 BP ＝ CD . 从而得到 PA ， AB ， PC 的数量关系． ∴∠ BAC ＝ ∠ CPB ，∠ ABC ＝ ∠ APC ， 又 ∵ ∠ APC ＝ ∠ CPB ＝ 60° ，∴∠ ABC ＝ ∠ BAC ＝ 60° ，∴△ ABC 为等边三角形； (2) PC ＝ PA ＋ PB . 证明：如答图，在 PC 上截取 PD ＝ AP ，连 结 AD . ∵∠ APC ＝ 60° ，∴△ APD 是等边三角形， ∴ AD ＝ AP ＝ PD ，∠ ADP ＝ 60° ， 即 ∠ ADC ＝ 120°. 又 ∵∠ APB ＝ ∠ APC ＋ ∠ BPC ＝ 120° ， ∴∠ ADC ＝ ∠ APB ， 变式跟进 2 答图 【 点悟 】 　 (1) 由圆周角与圆心角的关系可知：圆周角定理是建立在圆心角的基础上的，有了圆周角定理，就多了一种证明角相等关系或倍分关系的方法； (2) 直径所对圆周角为直角，反之亦成立，在圆的有关证明和计算中要创造条件，灵活运用，使问题简单化． 必明 3 易错点 1 ．弦和弧的两个端点都在圆上，但弦是线段，弧是曲线． 2 ．直径是圆中最长的弦，半径不是弦；半圆不是直径． 3 ．应用圆心角、弦、弧、弦心距的关系时，前提条件是 “ 在同圆或等圆中 ” ，它提供了圆心角、弧、弦、弦心距之间的转化方法．如果没有 “ 在同圆或等圆中 ” 这个前提条件，在应用时推出的结论是错误的． 圆的计算中谨防漏解 [ 襄阳中考 ] 圆的半径为 13 cm ，两弦 AB ∥ CD ， AB ＝ 24 cm ， CD ＝ 10 cm ，则两弦 AB ， CD 的距离是 ( 　　 ) A ． 7 cm 　　　　　 B ． 17 cm C ． 12 cm 　　　　　 D ． 7 cm 或 17 cm 【 错解 】 如答图 ① ，过点 O 作 OE ⊥ CD ，交 AB 于 F ，交 CD 于 E ，连结 OB ， OD . ∵ CD ＝ 10 cm ， ∴ DE ＝ 5 cm. ∵ OD ＝ 13 cm ， ∴ OE ＝ 12 cm. 同理 OF ＝ 5 cm ，∴ EF ＝ 7 cm. 故选 A. 【 错因 】 当已知条件中没有明确的图时，要注意分类讨论，错解忽略这一点，造成丢解．此题可以分两种情况，即两弦在圆心的同一侧时和在两侧时，所以此题的答案有两个． 易错警示答图 ① 【 正解 】 第一种情况：两弦在圆心的一侧时， 即错解结论；第二种情况：如答图 ② ，两弦 在圆心的不同侧，此时 EF ＝ OE ＋ OF ＝ 17 cm. 故选 D. 易错警示答图 ②