安徽2017中考数学试题 16页

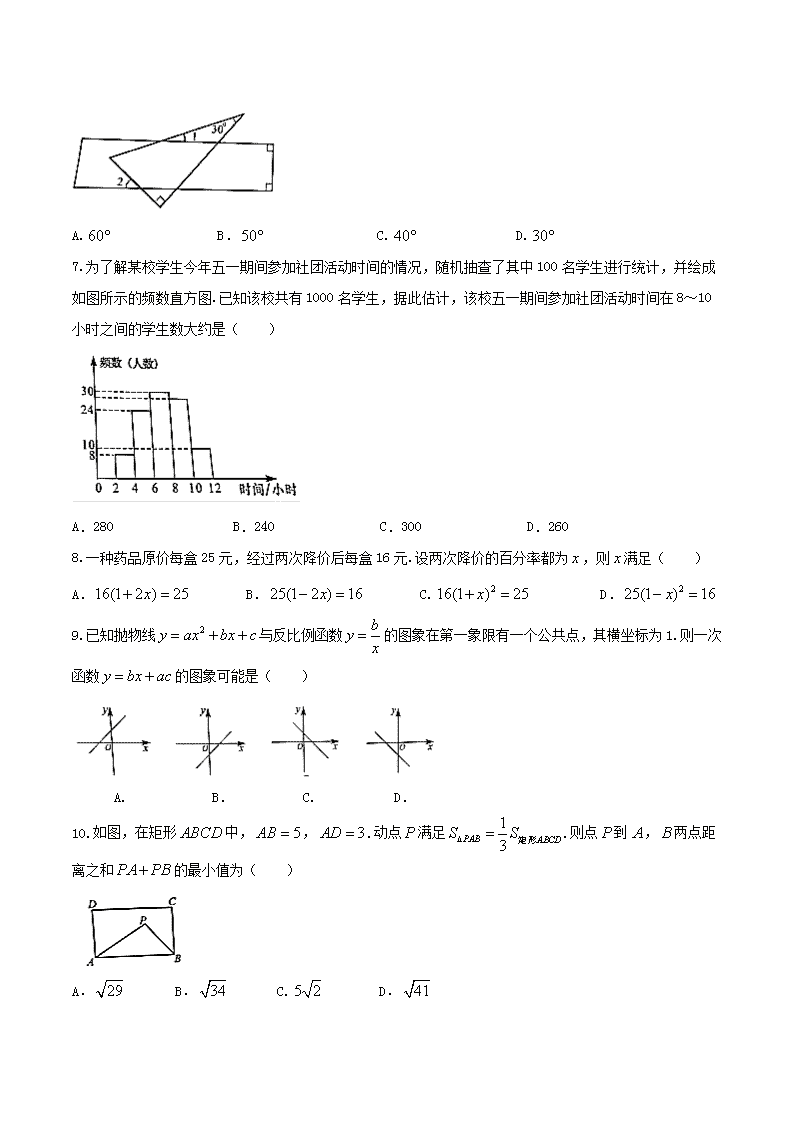
2017 年安徽省初中学业水平考试 数学 （试题卷） 一、选择题（本题共 10 个小题,每小题 4 分，满分 40 分） 每小题都给出 A、B、C、D 四个选项，其中只有一个是正确的. 1. 的相反数是（ ） A． B． C．2 D．-2 2.计算 的结果是（ ） A． B． C． D． 3.如图，一个放置在水平实验台上的锥形瓶，它的俯视图为（ ） A. B. C. D． 4.截至 2016 年底，国家开发银行对“一带一路”沿线国家累积发放贷款超过 1600 亿美元.其中 1600 亿用 科学计数法表示为（ ） A. B． C. D． 5.不等式 的解集在数轴上表示为（ ） A． B． C. D． 6.直角三角板和直尺如图放置.若 ，则 的度数为（ ） 1 2 1 2 − 1 2 − 2 2( )a− 6a 6a− 5a− 5a 1016 10× 101.6 10× 111.6 10× 120.16 10× 3 2 0x− > 1 20∠ = ° 2∠ A. B． C. D. 7.为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中 100 名学生进行统计，并绘成 如图所示的频数直方图.已知该校共有 1000 名学生，据此估计，该校五一期间参加社团活动时间在 8～10 小时之间的学生数大约是（ ） A．280 B．240 C．300 D．260 8.一种药品原价每盒 25 元，经过两次降价后每盒 16 元.设两次降价的百分率都为 ，则 满足（ ） A． B． C. D． 9.已知抛物线 与反比例函数 的图象在第一象限有一个公共点，其横坐标为 1.则一次 函数 的图象可能是（ ） A. B． C. D． 10.如图，在矩形 中， ， .动点 满足 .则点 到 ， 两点距 离之和 的最小值为（ ） A． B． C. D． 60° 50° 40° 30° x x 16(1 2 ) 25x+ = 25(1 2 ) 16x− = 216(1 ) 25x+ = 225(1 ) 16x− = 2y ax bx c= + + by x = y bx ac= + ABCD 5AB = 3AD = P 1 3PAB ABCDS S∆ = 矩形 P A B PA PB+ 29 34 5 2 41 二、填空题（本大题共 4 小题，每小题 5 分，满分 20 分） 11.27 的立方根是 ． 12.因式分解： = ． 13.如图，已知等边 的边长为 6，以 为直径的⊙ 与边 ， 分别交于 ， 两点，则劣弧 的长为 ． 14.在三角形纸片 中， ， ， .将该纸片沿过点 的直线折叠，使点 落在斜边 上的一点 处，折痕记为 （如图 1），剪去 后得到双层 （如图 2），再沿 着边 某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形.则所得平行四 边形的周长为 cm. 三、（本大题共 2 小题，每小题 8 分，满分 16 分） 15.计算： . 16.《九章算术》中有一道阐述“盈不足术”的问题，原文如下： 今有人共买物，人出八，盈三；人出七，不足四.问人数，物价各几何？ 译文为： 现有一些人共同买一个物品，每人出 8 元，还盈余 3 元；每人出 7 元，则还差 4 元.问共有多少人？这个物 品的价格是多少？ 请解答上述问题. 四、（本大题共 2 小题，每小题 8 分，满分 16 分） 17.如图，游客在点 处坐缆车出发，沿 的路线可至山顶 处.假设 和 都是直线段，且 ， ， ，求 的长. （参考数据： ， ， ） 2 4 4a b ab b− + ABC∆ AB O AC BC D E DE ABC 90A∠ = ° 30C∠ = ° 30AC cm= B A BC E BD CDE∆ BDE∆ BDE∆ 11| 2 | cos60 ( )3 −− × °− A A B D− − D AB BD 600AB BD m= = 75α = ° 45β = ° DE sin 75 0.97° ≈ cos75 0.26° ≈ 2 1.41≈ 18. 如图，在边长为 1 个单位长度的小正方形组成的网格中，给出了格点 和 （顶点为网格线 的交点），以及过格点的直线 . （1）将 向右平移两个单位长度，再向下平移两个单位长度，画出平移后的三角形； （2）画出 关于直线 对称的三角形； （3）填空： . 五、（本大题共 2 小题，每小题 10 分，满分 20 分） 19.【阅读理解】 我们知道， ，那么 结果等于多少呢？ 在图 1 所示三角形数阵中，第 1 行圆圈中的数为 1，即 ；第 2 行两个圆圈中数的和为 ，即 ；……；第 行 个圆圈中数的和为 ，即 .这样，该三角形数阵中共有 个圆圈， 所有圆圈中数的和为 . 【规律探究】 将桑拿教学数阵经两次旋转可得如图所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数 （如第 行的第一个圆圈中的数分别为 ，2， ），发现每个位置上三个圆圈中数的和均为 . ABC∆ DEF∆ l ABC∆ DEF∆ l C E∠ + ∠ = ° ( 1)1 2 3 2 n nn ++ + + + = 2 2 2 21 2 3 n+ + + + 21 2 2+ 22 n n n n n n n+ + +个 2n ( 1) 2 n n + 2 2 2 21 2 3 n+ + + + 1n − 1n − n 由此可得，这三个三角形数阵所有圆圈中数的总和为： .因此， = . 【解决问题】 根据以上发现，计算 的结果为 . 20.如图，在四边形 中， ， ， 不平行于 ，过点 作 交 的外接圆 于点 ，连接 . （1）求证：四边形 为平行四边形； （2）连接 ，求证： 平分 . 六、（本题满分 12 分） 21. 甲、乙、丙三位运动员在相同条件下各射靶 10 次，每次射靶的成绩如下： 甲：9，10，8，5，7，8，10，8，8，7； 乙：5，7，8，7，8，9，7，9，10，10； 丙：7，6，8，5，4，7，6，3，9，5. （1）根据以上数据完成下表： 平均数 中位数 方差 甲 8 8 乙 8 8 2.2 丙 6 3 （2）依据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由； （3）比赛时三人依次出场，顺序由抽签方式决定.求甲、乙相邻出场的概率. 2 2 2 23(1 2 3 )n+ + + + = 2 2 2 21 2 3 n+ + + + 2 2 2 21 2 3 2017 1 2 3 2017 + + + + + + + +   ABCD AD BC= B D∠ = ∠ AD BC C / /CE AD ABC∆ O E AE AECD CO CO BCE∠ 七、（本题满分 12 分） 22.某超市销售一种商品，成本每千克 40 元，规定每千克售价不低于成本，且不高于 80 元.经市场调查， 每天的销售量 （千克）与每千克售价 （元）满足一次函数关系，部分数据如下表： 售价 （元/千克） 50 60 70 销售量 （千克） 100 80 60 （1）求 与 之间的函数表达式； （2）设商品每天的总利润为 （元），求 与 之间的函数表达式（利润=收入-成本）； （3）试说明（2）中总利润 随售价 的变化而变化的情况，并指出售价为多少元时获得最大利润，最大 利润是多少？ 八、（本题满分 14 分） 23.已知正方形 ，点 为边 的中点. （1）如图 1，点 为线段 上的一点，且 ，延长 ， 分别与边 ， 交于点 ， . ①求证： ； ②求证： . （2）如图 2，在边 上取一点 ，满足 ，连接 交 于点 ，连接 延长交 于点 ，求 的值. y x x y y x W W x W x ABCD M AB G CM 90AGB∠ = ° AG BG BC CD E F BE CF= 2BE BC CE= ⋅ BC E 2BE BC CE= ⋅ AE CM G BG CD F tan CBF∠ 2017 年中考数学参考答案 一、1-5：BABCD 6-10：CADBD 二、11、3 12、 13、 14、 或 三、15、解：原式 . 16、解：设共有 人，根据题意，得 ， 解得 ，所以物品价格为 (元). 答：共有 7 人，物品的价格为 53 元. 四、17、解：在 中，由 得， (m). 在 中，由 可得， (m). 所以 (m). 18、(1)如图所示；(2)如图所示；(3)45 五、19、 1345 20、(1)证明：∵ ， ，∴ ， ∵ ，∴ . ∴ ，∴ . ∴四边形 是平行四边形. (2)证明：过点 作 ， ，垂足分别为 、 . ∵四边形 是平行四边形，∴ . 又 ，∴ ，∴ ，∴ 平分 . 六、21、解：(1) ( )22b a - p 40 80 3 3 12 3 22= ´ - = - x 8 3 7 4x x- = + 7x = 8 7 3 53´ - = Rt BDF△ sin DF BDb = 2sin 600 sin 45 600 300 2 4232DF BD b= × = ´ = ´ =° ≈ Rt ABC△ cos BC ABa = cos 600 cos75 600 0.26 156BC AB a= × = ´ = ´ =° 423 156 579DE DF EF DF BC= + = + = + = 2 1n + ( ) ( )12 1 2 n nn ++ × ( )( )1 1 2 16 n n n+ + B D=∠ ∠ B E=∠ ∠ D E=∠ ∠ CE AD∥ 180E DAE+ =∠ ∠ ° 180D DAE+ =∠ ∠ ° AE CD∥ AECD O OM EC^ ON BC^ M N AECD AD EC= AD BC= EC BC= OM ON= CO BCE∠ 平均数 中位数 方差 甲 2 乙 丙 6 (2)因为 ，所以 ，这说明甲运动员的成绩最稳定. (3)三人的出场顺序有(甲乙丙)，(甲丙乙)，(乙甲丙)，(乙丙甲)，(丙甲乙)，(丙乙甲)共 6 种，且每一种结果 出现的可能性相等，其中，甲、乙相邻出场的结果有(甲乙丙)，(乙甲丙)，(丙甲乙)，(丙乙甲)共 4 种，所以 甲、乙相邻出场的概率 . 七、22.解：(1)设 ，由题意，得 ，解得 ，∴所求函数表达式为 . (2) . (3) ，其中 ，∵ ， ∴当 时， 随 的增大而增大，当 时， 随 的增大而减小，当售价为 70 元时，获 得最大利润，这时最大利润为 1800 元. 八、23、(1)①证明：∵四边形 为正方形，∴ ， ， 又 ，∴ ，又 ，∴ ， ∴ (ASA)，∴ . ②证明：∵ ，点 为 中点，∴ ，∴ ， 又∵ ，从而 ，又 ，∴ ， ∴ ，即 ，由 ，得 . 由①知， ，∴ ，∴ . (2)解：(方法一) 延长 ， 交于点 (如图 1)，由于四边形 是正方形，所以 ， ∴ ，又 ，∴ ， 故 ，即 ， ∵ ， ，∴ ，由 知， ， 又 ，∴ ，不妨假设正方形边长为 1， 设 ，则由 ，得 ， 解得 ， (舍去)，∴ ， 于是 , 2 2.2 3< < 2 2 2s s s< <甲 乙 丙 4 2 6 3P = = y kx b= + 50 100 60 80 k b k b ì + =ïí + =ïî 2 200 k b ì = -ïí =ïî 2 200y x= - + ( )( ) 240 2 200 2 280 8000W x x x x= - - + = - + - ( )222 280 8000 2 70 1800W x x x= - + - = - - + 40 80x£ £ 2 0- < 40 70x£ < W x 70 80x< £ W x ABCD AB BC= 90ABC BCF= =∠ ∠ ° 90AGB =∠ ° 90BAE ABG+ =∠ ∠ ° 90ABG CBF+ =∠ ∠ ° BAE CBF=∠ ∠ ABE BCF△ ≌△ BE CF= 90AGB =∠ ° M AB MG MA MB= = GAM AGM=∠ ∠ CGE AGM=∠ ∠ CGE CGB=∠ ∠ ECG GCB=∠ ∠ CGE CBG△ ∽△ CE CG CG CB= 2CG BC CE= × CFG GBM CGF= =∠ ∠ ∠ CF CG= BE CF= BE CG= 2BE BC CE= × AE DC N ABCD AB CD∥ N EAB=∠ ∠ CEN BEA=∠ ∠ CEN BEA△ ∽△ CE CN BE BA= BE CN AB CE× = × AB BC= 2BE BC CE= × CN BE= AB DN∥ CN CG CF AM GM MB= = AM MB= FC CN BE= = BE x= 2BE BC CE= × ( )2 1 1x x= × - 1 5 1 2x -= 2 5 1 2x - -= 5 1 2 BE BC -= 5 1tan 2 FC BECBF BC BC -= = =∠ (方法二) 不妨假设正方形边长为 1，设 ，则由 ，得 ， 解得 ， (舍去)，即 ， 作 交 于 (如图 2)，则 ，∴ ， 设 ，则 ， ，∵ ，即 ， 解得 ，∴ ，从而 ，此时点 在以 为直径的圆上， ∴ 是直角三角形，且 ， 由(1)知 ，于是 . BE x= 2BE BC CE= × ( )2 1 1x x= × - 1 5 1 2x -= 2 5 1 2x - -= 5 1 2BE -= GN BC∥ AB N MNG MBC△ ∽△ 1 2 MN MB NG BC= = MN y= 2GN y= 5GM y= GN AN BE AB= 1 2 2 15 1 2 yy + = - 1 2 5 y = 1 2GM = GM MA MB= = G AB AGB△ 90AGB =∠ ° BE CF= 5 1tan 2 FC BECBF BC BC -= = =∠