2014年1月闸北中考数学一模试题 9页

图 1 F G E D CB A 图 2 l2l1 F E D C B A 闸北区九年级数学学科期末练习卷（2014 年 1 月） （考试时间：100 分钟，满分：150 分） 一、 选择题（本大题共 6 题，每题 4 分，满分 24 分） 1．对一个图形进行放缩时，下列说法中正确的是（ ） A．图形中线段的长度与角的大小都会改变； B．图形中线段的长度与角的大小都保持不变； C．图形中线段的长度保持不变、角的大小可以改变； D．图形中线段的长度可以改变、角的大小保持不变． 2．已知点 C 是线段 AB 上的一个点，且满足 ,则下列式子成立的是（ ） A． ； B． ； C． ； D． ． 3．下列关于抛物线 和 的关系说法中，正确的是（ ） A．它们的形状相同，开口也相同； B．它们都关于 轴对称； C．它们的顶点不相同； D．点（ ， ）既在抛物线 上也在 上． 4．下列关于向量的说法中，不正确．．．的是（ ） A． ； B． ； C．若 ，则 或 ； D． ． 5．已知 、 都是锐角，如果 ，那么 与 之间满足的关系是（ ） A． ； B． °； C． °；D． °． 6．如图 1，平行四边形 ABCD 中，F 是 CD 上一点，BF 交 AD 的 延长线于 G，则图中的相似三角形对数共有（ ） A．8 对； B． 6 对； C．4 对； D．2 对． 二、填空题（本大题共 12 题，每题 4 分，满分 48 分） 7．已知 ，则 ． 8．如图 2，已知 AD∥BE∥CF，它们依次交直线 、 于 点 A、B、C 和点 D、E、F，如果 DE:EF=3:5，AC=24， 则 BC= ． 9．在 Rt△ABC 和 Rt△DEF 中，∠ C=∠ F=90°，当 AC=3，AB=5，DE=10，EF=8 时， Rt△ABC 和 Rt△DEF 是 的．（填“相似”或者“不相似”） 2AC BC AB 51 2 AC BC  51 2 AC AB  51 2 BC AB  51 2 CB AC  21 3yx 21 3yx y 3 3 2( ) 2 2a b a b   22aa 2ab 2ab 2ab ( ) ( )m na mn a   sin cos  90 90 90 : 3: 2ab ( ) :a b a 1l 2l 图 3 D C P G F E CB A 图 5 图 4 G D E F CB A 10．如果两个相似三角形的对应边上的高之比是 2:3，则它们的周长比是 ． 11．化简： ． 12．如图 3，某人在塔顶的 P 处观测地平面上点 C 处，经测量∠ P=35°， 则他从 P 处观察 C 处的俯角是 度． 13．将二次函数 的图像向下平移 1 个单位后，它的顶点 恰好落在 轴上，则 ． 14．在 Rt△ABC 中，∠C=90°，CD⊥AB 于点 D，若 AD=9，BD=4，则 AC= ． 15．一个边长为 3 厘米的正方形，若它的边长增加 厘米，面积随之增加 平方厘米，则 关于 的函数解析式是 ．（不写定义域） 16．如图 4，在平行四边形 ABCD 中，AB=12，AD=18， ∠BAD 的平分线交 BC 于点 E，交 DC 的延长线于点 F， BG⊥AE，垂足为 G，BG= ，则△CEF 的周长是 ． 17．如图 5，点 G 是 Rt△ABC 的重心，过点 G 作矩形 GECF， 当 GF：GE=1：2 时，则∠ B 的正切值为 ． 18．如图 6，已知等腰△ABC，AD 是底边 BC 上的高， AD：DC=1：3，将△ADC 绕着点 D 旋转，得△DEF， 点 A、C 分别与点 E、F 对应，且 EF 与直线 AB 重合， 设 AC 与 DF 相交于点 O，则 = ． 三、解答题（本大题共 7 题，满分 78 分） 19．（本题满分 10 分，第（1）小题满分 4 分，第（2）小题满分 4 分，第（3）小题满分 2 分） 已知：抛物线 经过 A（ ，0）、B（5，0）两点，顶点为 P． 求：（1）求 b，c 的值； （2）求△ABP 的面积； （3）若点 C（ ， ）和点 D（ ， ）在该抛物线上，则当 时， 请写出 与 的大小关系． CD AB BC   2 2y x x m   x m  y 82 :AOF DOCSS 2y x b x c    1 1x 1y 2x 2y 1201xx   图 6 D CB A 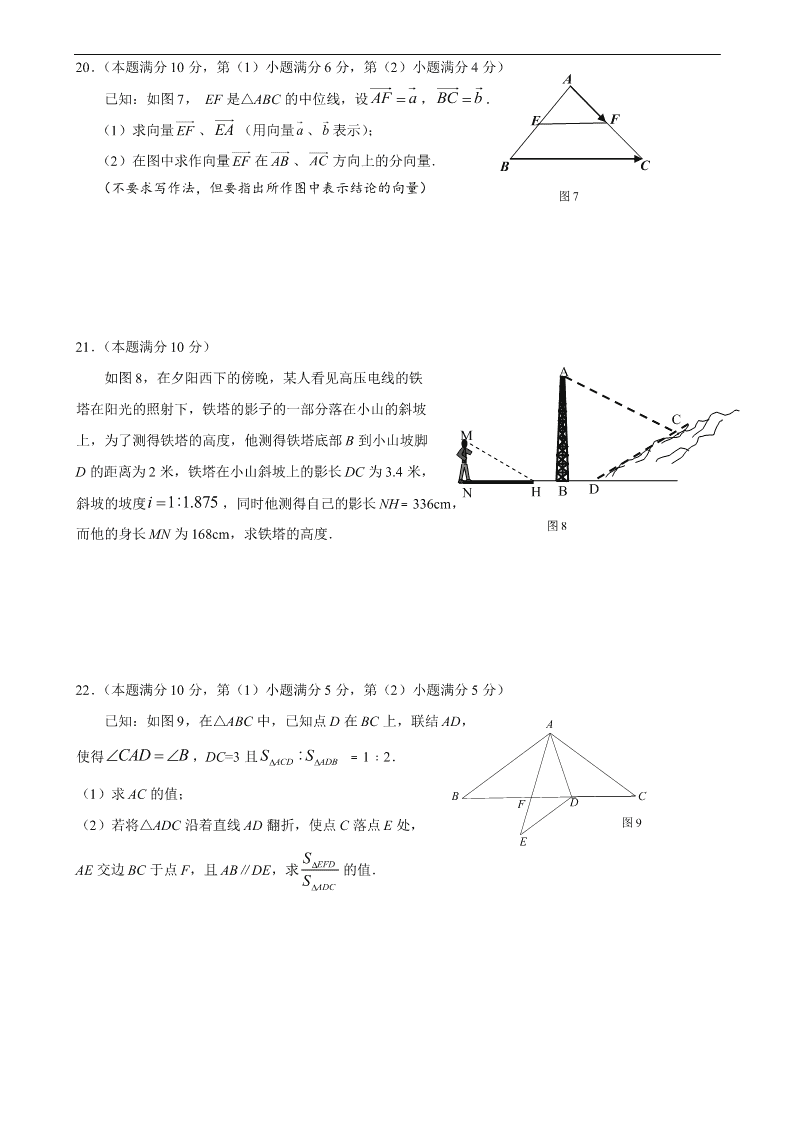20．（本题满分 10 分，第（1）小题满分 6 分，第（2）小题满分 4 分） 已知：如图 7， EF 是△ABC 的中位线，设 ， ． （1）求向量 、 （用向量 、 表示）； （2）在图中求作向量 在 、 方向上的分向量． （不要求写作法，但要指出所作图中表示结论的向量） 21．（本题满分 10 分） 如图 8，在夕阳西下的傍晚，某人看见高压电线的铁 塔在阳光的照射下，铁塔的影子的一部分落在小山的斜坡 上，为了测得铁塔的高度，他测得铁塔底部 B 到小山坡脚 D 的距离为 2 米，铁塔在小山斜坡上的影长 DC 为 3.4 米， 斜坡的坡度 ，同时他测得自己的影长 NH﹦336cm， 而他的身长 MN 为 168cm，求铁塔的高度． 22．（本题满分 10 分，第（1）小题满分 5 分，第（2）小题满分 5 分） 已知：如图 9，在△ABC 中，已知点 D 在 BC 上，联结 AD， 使得 ，DC=3 且 ﹦1﹕2． （1）求 AC 的值； （2）若将△ADC 沿着直线 AD 翻折，使点 C 落点 E 处， AE 交边 BC 于点 F，且 AB∥DE，求 的值． AF a BC b EF EA a b AB AC 1 1.875i  : CAD B   ACD ADBSS: EFD ADC S S   A B C E F 图 7 A B C D M N H 图 8 F E D CB A 图 9 图 10 CB A 23．（本题满分 12 分，第（1）小题满分 5 分，第（2）小题满分 7 分） 小华同学学习了第二十五章《锐角三角比》后，对求三角形 的面积方法进行了研究，得到了新的结论： （1）如图 10，已知锐角△ABC．求证： ； （2）根据题（1）得到的信息，请完成下题：如图 11，在等腰 △ABC 中，AB=AC=12 厘米，点 P 从 A 点出发，沿着边 AB 移动， 点 Q 从 C 点出发沿着边 CA 移动，点 Q 的速度是 1 厘米/秒，点 P 的速度是点 Q 速度的 2 倍，若它们同时出发，设移动时间为 t 秒， 问：当 t 为何值时， ? 24．（本题满分 12 分，第（1）小题满分 6 分，第（2）小题满分 6 分） 已知：如图 12，抛物线 与 轴交于点 C， 与 轴交于点 A、B，（点 A 在点 B 的左侧）且满足 OC=4OA． 设抛物线的对称轴与 x 轴交于点 M： （1）求抛物线的解析式及点 M 的坐标； （2）联接 CM，点 Q 是射线 CM 上的一个动点，当 △QMB 与△COM 相似时，求直线 AQ 的解析式． 1 sin2ABCS AB AC A  3 8 APQ ABC S S    24 45y x mx    y x CB A 图 11 B A C 图 12 O x y 25．（本题满分 14 分，第（1）小题满分 6 分，第（2）小题满分 4 分，第（3）小题满分 4 分） 已知：如图 13，在等腰直角△ ABC 中， AC = BC，斜边 AB 的长为 4，过点 C 作射线 CP//AB，D 为 射线 CP 上一点，E 在边 BC 上（不与 B、C 重合），且∠DAE=45°，AC 与 DE 交于点 O． （1）求证：△ADE∽△ACB； （2）设 CD=x， BAE = y，求 y 关于 x 的函数 解析式，并写出它的定义域； （3）如果△COD 与△BEA 相似，求 CD 的值． tan 图 13 P D O EC B A D F CB A E 九年级数学学科期末练习卷（2014 年 1 月） 答案及评分参考 （考试时间：100 分钟，满分：150 分） 一、选择题（本大题共 6 题，每题 4 分，满分 24 分） 题号 1 2 3 4 5 6 答案 D B B C B B 二、填空题（本大题共 12 题，每题 4 分，满分 48 分） 7、 ． 8、15． 9、相似． 10、2:3． 11、 ． 12、55． 13、2． 14、 ． 15、 ． 16、16． 17、 ． 18、 ． 三、解答题（本大题共 12 题，满分 78 分） 19、（本题满分 10 分，第（1）小题满分 4 分，第（2）小题满分 4 分，第（3）小题满分 2 分） 解：（1）把点 A（ ，0）、B（5，0）分别代入 ，得 …………………………………………………………（1+1 分） 解得 ． …………………………………………………………（1+1 分） （2）由（1）得抛物线解析式 ∴ ∴P（2，9） …………………………………………………………（2 分） ∵A（ ，0）、B（5，0） ∴AB=6 …………………………………………………………（1 分） ∴ ． …………………………………………………………（1 分） （3）∵抛物线开口向下 ∴在对称轴直线 x=2 的左侧 y 随着 x 的增大而增大 ∴ ＜ ． …………………………………………………………（2 分） 20、（本题满分 10 分，第（1）小题满分 6 分，第（2）小题满分 4 分） （1）∵EF 是△ABC 的中位线 ∴EF∥BC，EF= ………………………………………………………（2 分） ∵ ∴ ………………………………………………………（1 分） ∵ , ………………………………………………………（2 分） ∴ ． ………………………………………………………（1 分） （2） 1 3 AD 3 13 2 6y x x 1 2 32 45 1 2y x b x c    01 0 25 5 bc bc          4 5 b c    2 45y x x    2( 2) 9yx    1 6 9 272ABPS     1y 2y 1 2 BC BC b EF 1 2 b EA EF FA AF a 1 2EA b a FE 1 2 3 D CB A 图 10 所以 、 是 在 和 方向上的分向量．……………………………（2 分） （评分说明：准确作出向量 、 各得 1 分，结论 2 分） 21、（本题满分 10 分） 解：过点 C 作 CE⊥BD 于点 E，延长 AC 交 BD 延长线于点 F ………………（1 分） 在 Rt△CDE 中， ∴ ………………………（1 分） 设 CE=8x ,DE=15x ，则 CD=17x ∵DC=3.4 米 ∴CE=1.6 米，DE=3 米 ………………………（2 分） 在 Rt△MNH 中， tan∠MHN …………………（1 分） ∴在 Rt△ABF 中，tan∠F tan∠MHN …………………………（1 分） ∴EF=3.2 米 …………………………（1 分） 即 BF=2+3+3.2=8.2 米 …………………………（1 分） ∴在 Rt△CEF 中，tan∠F ∴AB=4.1 米 …………………………（1 分） 答：铁塔的高度是 4.1 米． …………………………（1 分） 22、（本题满分 10 分，第（1）小题满分 5 分，第（2）小题满分 5 分） 解：（1）∵ ﹦1﹕2 ∴CD：BD=1:2 ……………………………（1 分） ∵DC=3 ∴BD=6 ……………………………（1 分） 在△ACD 和△BCA 中，∠CAD=∠B，∠C=∠C ∴△ACD∽△BCA ……………………………（1 分） ∴ 即 …………………………………………………（1 分） ∴ ． …………………………………………………（1 分） （2）∵翻折 ∴∠C=∠E，∠1=∠2，DE=DC=3 …………………………………………………（1 分） ∵AB∥DE ∴∠3=∠B ……………………………………………………………………（1 分） ∵∠1=∠B ∴∠1=∠3 …………………………………………………（1 分） ∴△ACD∽△DEF …………………………………………………（1 分） ∴ ． …………………………………………………（1 分） 23．（本题满分 12 分，第（1）小题满分 5 分，第（2）小题满分 7 分） 解：（1）如图 10，过点 C 作 CD⊥ AB 于点 D……………（1 分） 在 Rt△ADC 中，sinA= ……………………………（1 分） ∴CD=AC.sinA ……………………………（1 分） EA ED EF AB AC 1 1.875i  : 18 1.875 15 CE DE  168 1 336 2 MN NH   1.6CE EF EF 1 2 1 2 AB BF ACD ADBSS: CD AC AC CB 2AC CD CB 33AC  2 1()3 EFD ADC S DE S AC    CD AC F E D CB A 图 9 ∵ ……………………………（1 分） ∴ ．……………………………（1 分） （2）根据题意：AP=2t 厘米 ，CQ=t 厘米 ∴AQ=（12—t）厘米 ………………………………（1 分） 由（1）得： …………………（1 分） ∴ …………（1 分） 化简得： …………………………………（1 分） 解得 （舍）， …………………………………（2+1 分） 即当 t=3 秒时， ． 24．（本题满分 12 分，第（1）小题满分 6 分，第（2）小题满分 6 分） 解：（1）根据题意：C（0，4）……………………………（1 分） ∵OC=4OA ∴A（ ，0）………………………………………………（1 分） 把点 A 代入得 0= ……………………………（1 分） 解得 ………………………………………………（1 分） ∴抛物线的解析式 …………………（1 分） ∴ ………………………………………………（1 分） （2）根据题意得：BM=3，tan∠CMO= 2，直线 CM：y= x+4 （i）当∠COM=∠MBQ=90°时，△COM∽△QBM ∴tan∠BMQ= ∴BQ=6 即 Q（5， ） ……………………………………（2 分） ∴AQ： ……………………………………（1 分） （i i）当∠COM=∠BQM=90°时，△COM∽△BQM 同理 Q（ ） …………………………………（2 分） ∴AQ： …………………………………（1 分） 25．（本题满分 14 分，第（1）小题满分 6 分，第（2）小题满分 4 分，第（3）小题满分 4 分） （1）证明：∵△ACB 是等腰直角三角形 ∴∠CAB＝∠B=45° ∵CP//AB ∴∠DCA＝∠CAB=45° …………………………………………………（1 分） ∴∠DCA＝∠B …………………………………………………（1 分） ∵∠ DAE=45° 1 2ABCS AB CD  1 sin2ABCS AB AC A  1 sin2APQS AP AQ A  1 sin 2 (12 ) 32 1 12 12 8sin2 APQ ABC AP AQ AS tt S AB AC A      2 12 27 0tt   1 9t  2 3t  3 8 APQ ABC S S    1 4 45 m   16= 5m 24 16 455y x x    24 16 455y x x    24 362)55x   （ (2 0)M ， 2 2BQ BM  6 1yx   13 6 55 ，- 11 33yx   Q P A B C 图 11 Q1 B A C 图 12 O x y M Q2 ∴∠ DAC+∠ CAE=∠ CAE+∠ EAB ∴∠ DAC =∠ EAB …………………………………………………（1 分） ∴△DCA∽△EAB …………………………………………………（1 分） ∴ 即 且∠ DAE =∠ CAB=45° ……………………………（1 分） ∴△ADE∽△ACB ． ……………………………………………（1 分） （2）过点 E 作 EH⊥AB 于点 H ……………………………………（1 分） 由（1）得△DCA∽△EAB ∴ ∵△ACB 是等腰直角三角形，且 CD=x ∴EB= x …………………（1 分） ∴EH=BH= x ∴AH=4—x 在 Rt△AEH 中， BAE = 即 y= ………………………………………………………（1 分） 定义域 0＜x＜2． ………………………………………………………（1 分） （3）若△COD 与△BEA 相似，又△BEA 与相似△DCA 即△COD 与△DCA 相似 ∴只有△DCO∽△ACD ……………………………………………（1 分） ∴ ∵∠DAO＝∠CEO ∴∠CEO＝∠EAB ∴tan∠CEO＝y 即 ∴ …………………………………………（1 分） ∴ 解得 ， ……………………………（1 分） 经检验 都是原方程的实数根， 不合题意舍去…（1 分） ∴当 CD= 时，△COD 与△BEA 相似． AD AC AE AB AD AE AC AB DC AC EB AB 2 tan EH AH 4 x x 2CD CO CA yCO CE   2 2 2 4 xCO x x  2x   2 2 2 2 24 xx x  1 4 2 2x  2 4 2 2x  12,xx 4 2 2 图 13 P D O EC B A H