黔东南州2021年中考数学模拟试题及答案（2） 16页

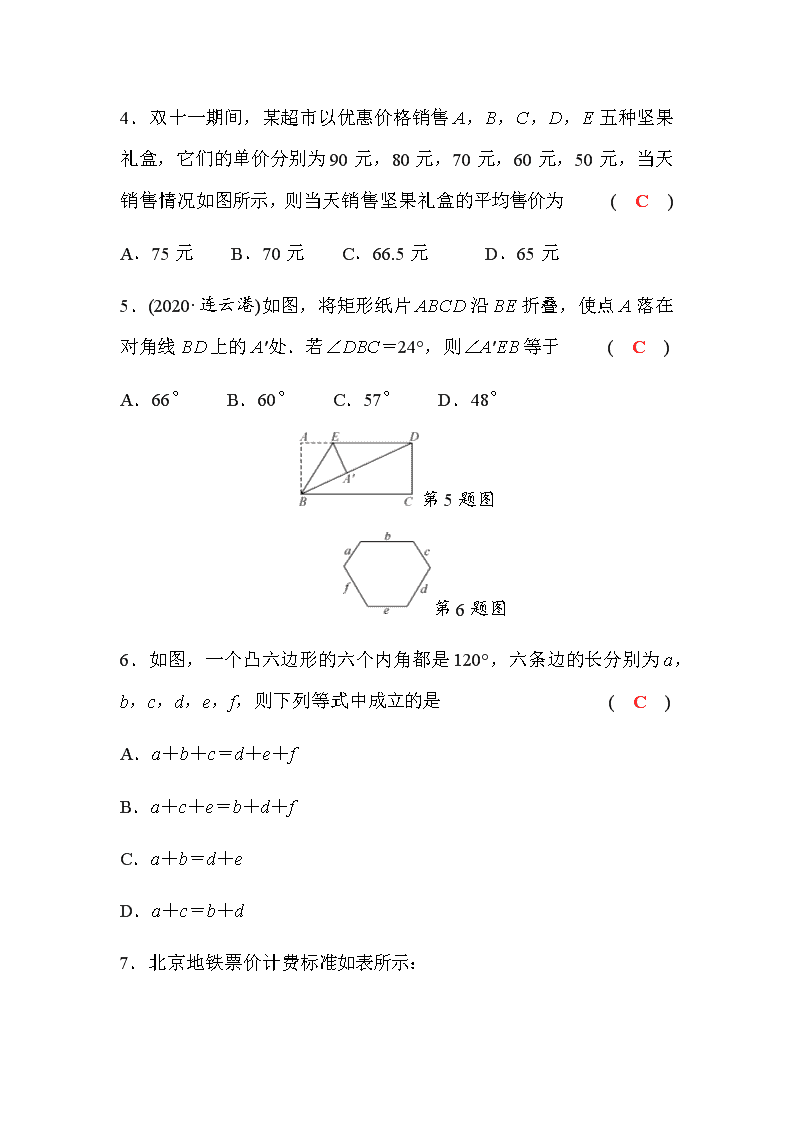
黔东南州、黔南州、黔西南州2021年初中毕业升学考试 数学 模拟卷(二)‎ ‎(考试时间：120分钟　　满分：150分)‎ 一、选择题(本大题共10小题，每小题4分，共40分)‎ ‎1．下列各对数中，互为相反数的是 (　C　)‎ A．－2与3 B．－(＋3)与＋(－3)‎ C．4与－4 D．5与 2． ‎(2020·宜宾)我国自主研发的北斗系统技术世界领先，2020年6月23日在西昌卫星发射中心成功发射最后一颗北斗三号组网卫星，该卫星发射升空的速度约为7 100米/秒．将7 100用科学记数法表示为 ‎ ‎(　D　)‎ A．7 100 B．0.71×104 C．71×102 D．7.1×103‎ ‎3．(2020·台州)无理数在 (　B　)‎ A．2和3之间 B．3和4之间 C．4和5之间 D．5和6之间 ‎4．双十一期间，某超市以优惠价格销售A，B，C，D，E五种坚果礼盒，它们的单价分别为90元，80元，70元，60元，50元，当天销售情况如图所示，则当天销售坚果礼盒的平均售价为 (　C　)‎ A．75元 B．70元 C．66.5元 　D．65元 ‎5．(2020·连云港)如图，将矩形纸片ABCD沿BE折叠，使点A落在对角线BD上的A′处．若∠DBC＝24°，则∠A′EB等于 (　C　)‎ A．66° B．60° C．57° D．48°‎ 第5题图 ‎　　　第6题图 ‎6．如图，一个凸六边形的六个内角都是120°，六条边的长分别为a，b，c，d，e，f，则下列等式中成立的是 (　C　)‎ A．a＋b＋c＝d＋e＋f B．a＋c＋e＝b＋d＋f C．a＋b＝d＋e D．a＋c＝b＋d ‎7．北京地铁票价计费标准如表所示：‎ 乘车距离 x(公里)‎ x≤6‎ ‎6＜x ‎≤12‎ ‎12＜x ‎≤22‎ ‎22＜x ‎≤32‎ x＞32‎ 票价(元)‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 每增加1元可 乘坐20公里 另外，使用市政交通一卡通，每个月每张卡片支出累计满100元后，超出部分打8折；满150元后，超出部分打5折；支出累计达400元后，不再打折．‎ 小红妈妈上班时，需要乘坐地铁15公里到达公司，每天上下班共乘坐两次，如果每次乘坐地铁都使用市政交通一卡通，那么每月第21次乘坐地铁上下班时，她刷卡支出的费用是 (　C　)‎ A．2.5元 B．3元 C．4元 D．5元 ‎8．等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程x2－6x＋n＝0的两根，则n的值为 (　B　)‎ A．8 B．9 C．9或8 D．8或10‎ ‎9．如图，点D，E分别在△ABC的两边BA，CA的延长线上，下列条件能判定ED∥BC的是 (　D　)‎ A．＝ B．＝ C．AD·AB＝DE·BC D．AD·AC＝AB·AE 第9题图 ‎　　　第10题图 ‎10．(2020·咸宁)如图，在⊙O中，OA＝2，∠C＝45°，则图中阴影部分的面积为 (　D　)‎ A．－ B．π－ C．－2 D．π－2‎ 二、填空题(本大题共10小题，每小题3分，共30分)‎ ‎11．分解因式：9y－x2y＝__y(3＋x)(3－x)__．‎ ‎12．若代数式1－8x与9x－3的值互为相反数，则x＝__2__．‎ ‎13．如图，反比例函数图象经过点A，过点A作AB⊥x轴，垂足为B，若△OAB的面积为3，则该反比例函数的解析式是__y＝__．‎ 第13题图 ‎　　第15题图 ‎14．(2020·泸州)函数y＝的自变量x的取值范围是__x≥2__．‎ ‎15．如图，△ABC中，D，E，F分别是各边的中点，随机地向△ABC中内掷一粒米，则米粒落到阴影区域内的概率是____．‎ ‎16．如图，在直线a的同侧有P，Q，R三点，若PQ∥a，QR∥a，则P，Q，R三点__在__(选填“在”或“不在”)同一条直线上．‎ ‎17．一个几何体由若干个棱长为1 cm的小正方形搭成，从正面，上面看到的这个几何体的形状图如图所示．若搭成的几何体，需要表面着色，那么它的着色面积最多为__24__cm2.‎ ‎18．一个不透明的布袋里装有100个只有颜色不同的球，这100个球中有m个红球．通过大量重复试验后发现，从布袋中随机摸出一个球，摸到红球的频率稳定在0.2左右，则m的值约为__20__．‎ ‎19．如图，在平面直角坐标系中，将矩形OABC沿OB对折，使点A落在点A1处，已知OA＝，AB＝1，则点A1的坐标是____．‎ ‎20．Pn表示多边形对角线的交点个数(指落在多边形内部的交点)如果这些交点都不重合(任意三条对角线不交于一点)，如图，四边形对角线交点个数P4＝1，五边形对角线交点个数P5＝5.通过推理发现Pn＝n···(其中a，b是常数n≥4)，则P12＝__495__．‎ ‎　　‎ 三、解答题(本大题共6小题，共80分)‎ ‎21．(12分)计算：‎ ‎(1)(π－3)0＋－2cos 45°－；‎ ‎(2)若x＋＝3，求的值．‎ 解：(1)原式＝1＋3－2×－8‎ ‎＝2－7.‎ ‎(2)原式＝ ‎＝，‎ ‎∵x＋＝3，‎ ‎∴原式＝＝＝.‎ ‎22．(12分)贵州省每年中考，都要进行体育测试，其中男生的测试项目有A“立定跳远”，B“1000米测试”，C“投掷实心球”，D“引体向上”四个．规定：每名学生测试三项，其中A，B为必测项目，第三项从C，D中随机抽取，每项10分，满分30分．‎ ‎(1)请用列表或画树状图，求甲，乙两同学测试的三个项目完全相同的概率；‎ ‎(2)据统计，九(1)班有8名男生抽到了C“投掷实心球”项目，他们的成绩如下：‎ ‎7，6，8，9，10，5，8，7‎ ‎①这组成绩的中位数是________，平均数是________；‎ ‎②该班男生丙因病错过了测试，补测抽到了C“投掷实心球”项目，加上丙同学的成绩后，发现这组成绩的众数与中位数相等，但平均数比①中的平均数大，则丙同学“投掷实心球”的成绩为______；‎ ‎(3)九(1)班有50名学生，下表是单项目成绩统计，请计算出该班此次体能测试的平均成绩．‎ 项目 A立定 跳远 B 1 000米 测试 C投掷 实心球 D引体 向上 测试人数(人)‎ ‎50‎ ‎50‎ ‎20‎ ‎30‎ 单项平均 成绩(分)‎ ‎9‎ ‎8‎ ‎7‎ ‎8‎ 解：(1)画树状图如图所示．‎ 由图中可知抽取结果共有4种，其中甲，乙两同学测试的项目完全相同的结果有2种，‎ 则P(三个项目完全相同的概率)＝＝.‎ (2) ‎①根据题意得：中位数是＝7.5，‎ 平均数＝＝7.5；‎ 故答案为7.5，7.5；‎ ‎②设丙同学“投掷实心球”的成绩为x，‎ 则这组成绩为5，6，7，7，x，8，8，9，10，‎ ‎∵这组成绩的众数与中位数相等，‎ ‎∴x为7或8，‎ ‎∵平均数比①中的平均数大，即x＞7.5，‎ ‎∴x＝8，故答案为8.‎ ‎(3)9＋8＋＝24.6，‎ 答：此次体能测试的平均成绩为24.6.‎ ‎23．(14分)如图，AB垂直平分线段CD(AB＞CD)，点E是线段CD延长线上的一点，且BE＝AB，连接AC，过点D作DG⊥AC于点G，‎ 交AE的延长线于点F.‎ ‎(1)若∠CAB＝α，则∠AFG＝______(用α的代数式表示)；‎ ‎(2)求证：AC＝DF；‎ ‎(3)若CD＝m，求EF的长．‎ ‎(1)解：∵AB＝BE，AB⊥BE.‎ ‎∴∠BAE＝∠AEB＝45°.‎ 在Rt△AGF中，∠AFG＋∠GAF＝90°.‎ ‎∵∠GAF＝∠CAB＋∠BAE＝45°＋α.‎ ‎∴∠AFG＝45°－α.‎ 答案为45°－α.‎ ‎(2)证明：连接AD，‎ ‎∵AB垂直平分线段CD，‎ ‎∴AC＝AD，‎ ‎∴∠ADC＝∠ACB＝90°－α，‎ ‎∴∠DAE＝∠ADC－45°＝45°－α，‎ ‎∴∠DAE＝∠AFD，∴AD＝DF，∴AC＝DF.‎ ‎(3)解：∵CD＝m，∴BD＝CB＝m，‎ 过F作FH⊥CE交CE的延长线于H，‎ 则△EHF是等腰直角三角形，∴FH＝HE，‎ ‎∵∠H＝∠ABC＝90°，‎ ‎∠CAB＝∠CDG＝∠FDH，AC＝DF，‎ ‎∴△ACB≌△DFH(AAS)，‎ ‎∴FH＝CB＝m，‎ ‎∴EF＝FH＝m.‎ ‎24．(14分)电商时代使得网购更加便捷和普及．小张响应国家号召，自主创业，开了家淘宝店．他购进一种成本为100元/件的新商品，在试销中发现：销售单价x(元)与每天销售量y(件)之间满足如图所示的关系．‎ ‎(1)求y与x之间的函数关系式；‎ ‎(2)若某天小张销售该产品获得的利润为1 200元，求销售单价x的值．‎ 解：(1)设y与x之间的函数关系式为y＝kx＋b(k≠0)，‎ 由所给函数图象可知 解得 故y与x的函数关系式为y＝－x＋180.‎ ‎(2)由题意得(－x＋180)(x－100)＝1 200，‎ 解得x＝120，或x＝160.‎ 答：若某天小张销售该产品获得的利润为1 200元，‎ 则销售单价为120元或160元．‎ ‎25．(12分)如图，AB是⊙O的直径，点C在⊙O上，连接BC，AC，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E.‎ ‎(1)求证：DE是⊙O的切线；‎ ‎(2)若＝，求cos ∠ABC的值．‎ ‎(1)证明：连接OC.‎ ‎∵AD是过点A的切线，AB是⊙O的直径，‎ ‎∴AD⊥AB，‎ ‎∴∠DAB＝90°.‎ ‎∵OD∥BC，∴∠1＝∠2，∠3＝∠4.‎ ‎∵OC＝OB，∴∠2＝∠4.∴∠1＝∠3.‎ 在△COD和△AOD中， ‎∴△COD≌△AOD(SAS)，‎ ‎∴∠OCD＝∠DAB＝90°，即OC⊥DE于点C.‎ ‎∵OC是⊙O的半径，∴DE是⊙O的切线．‎ ‎(2)解：由＝，可设CE＝2k(k＞0)，‎ 则DE＝3k，∵DA，DC是⊙O的切线．‎ ‎∴AD＝DC＝k.‎ ‎∴在Rt△DAE中，AE＝＝2k.‎ ‎∴tan E＝＝.‎ ‎∵在Rt△OCE中，tan E＝＝.‎ ‎∴＝，∴OC＝OA＝.‎ ‎∴在Rt△AOD中，OD＝＝k，‎ ‎∴cos ∠ABC＝cos ∠AOD＝＝.‎ ‎26．(16分)已知，抛物线y＝ax2＋bx＋c(a≠0)的顶点为A(s，t)(其中s≠0).‎ ‎(1)若抛物线经过(2，7)和(－3，37)两点，且s＝1.‎ ‎①求抛物线的解析式；‎ ‎②若n＞1，设点M(n，y1)，N(n＋1，y2)在抛物线上，比较y1，y2的大小关系，并说明理由；‎ ‎(2)若a＝2，c＝－2，直线y＝2x＋m与抛物线y＝ax2＋bx＋c的交于点P和点Q，点P的横坐标为h，点Q的横坐标为h＋3，求出b和h的函数关系式；‎ ‎(3)若点A在抛物线y＝x2＋3x＋c上，且2≤s＜3时，求a的取值范围．‎ 解：(1)①设抛物线的解析式为y＝a(x－1)2＋t，‎ 根据题意得解得 故抛物线的解析式为y＝2(x－1)2＋5＝2x2－4x＋7；‎ ‎②∵M(n，y1)，N(n＋1，y2)在抛物线上，‎ ‎∴y1＝2n2－4n＋7，y2＝2(n＋1)2－4(n＋1)＋7＝2n2＋5，‎ ‎∴y2－y1＝4n－2，‎ ‎∵n＞1，‎ ‎∴y2＞y1.‎ ‎(2)根据题意得yP＝2h＋m，yQ＝2h＋6＋m，‎ ‎∴yQ－yP＝6，‎ 又∵P，Q在抛物线上，‎ ‎∴yP＝2h2＋bh＋2，‎ yQ＝2h2＋(12＋b)h＋16＋3b.‎ ‎∴yQ－yP＝12h＋18＋3b.‎ ‎∴yQ－yP＝12h＋18＋3b＝6，‎ ‎∴b＝－4h－4.‎ ‎(3)设抛物线y＝a(x－s)2＋t.‎ ‎∵抛物线经过点(0，c)，‎ ‎∴c＝as2＋t，即c－t＝as2①，‎ 又∵点A在抛物线y＝x2＋3x＋c上，‎ ‎∴t＝s2＋3s＋c，即c－t＝－3s－s2②，‎ 由①②可得as2＝－3s－s2.即(a＋1)s2＝－3s.‎ 当a＝－1时，‎ ‎－3s＝0，‎ 解得s＝0，不成立；‎ 当a≠－1时，‎ ‎∵s≠0，‎ ‎∴s＝－ ‎∵2≤s＜3，‎ ‎∴－≤a＜－2.‎