2019年四川省巴中市中考数学试卷含答案 28页

‎2019年四川省巴中市中考数学试卷 一、选择题（本大题共10个小题，每小题4分，共40分，在每小题给出的四个选项中，只有一个选项是正确的，请使用2B铅笔将答題卡上对应题号的答案标号涂黑。）‎ ‎1．（4分）下列四个算式中，正确的是（　　）‎ A．a+a＝2a B．a5÷a4＝2a C．（a5）4＝a9 D．a5﹣a4＝a ‎2．（4分）在平面直角坐标系中，已知点A（﹣4，3）与点B关于原点对称，则点B的坐标为（　　）‎ A．（﹣4，﹣3） B．（4，3） C．（4，﹣3） D．（﹣4，3）‎ ‎3．（4分）企业家陈某，在家乡投资9300万元，建立产业园区2万余亩．将9300万元用科学记数法表示为（　　）‎ A．93×108元 B．9.3×108元 C．9.3×107元 D．0.93×108元 ‎4．（4分）如图是由一些小立方体与圆锥组合成的立体图形，它的主视图是（　　）‎ A． B． ‎ C． D．‎ ‎5．（4分）已知关于x、y的二元一次方程组ax-y=4‎‎3x+by=4‎的解是x=2‎y=-2‎，则a+b的值是（　　）‎ A．1 B．2 C．﹣1 D．0‎ ‎6．（4分）下列命题是真命题的是（　　）‎ A．对角线相等的四边形是矩形 ‎ B．对角线互相垂直的四边形是矩形 ‎ C．对角线互相垂直的矩形是正方形 ‎ D．四边相等的平行四边形是正方形 ‎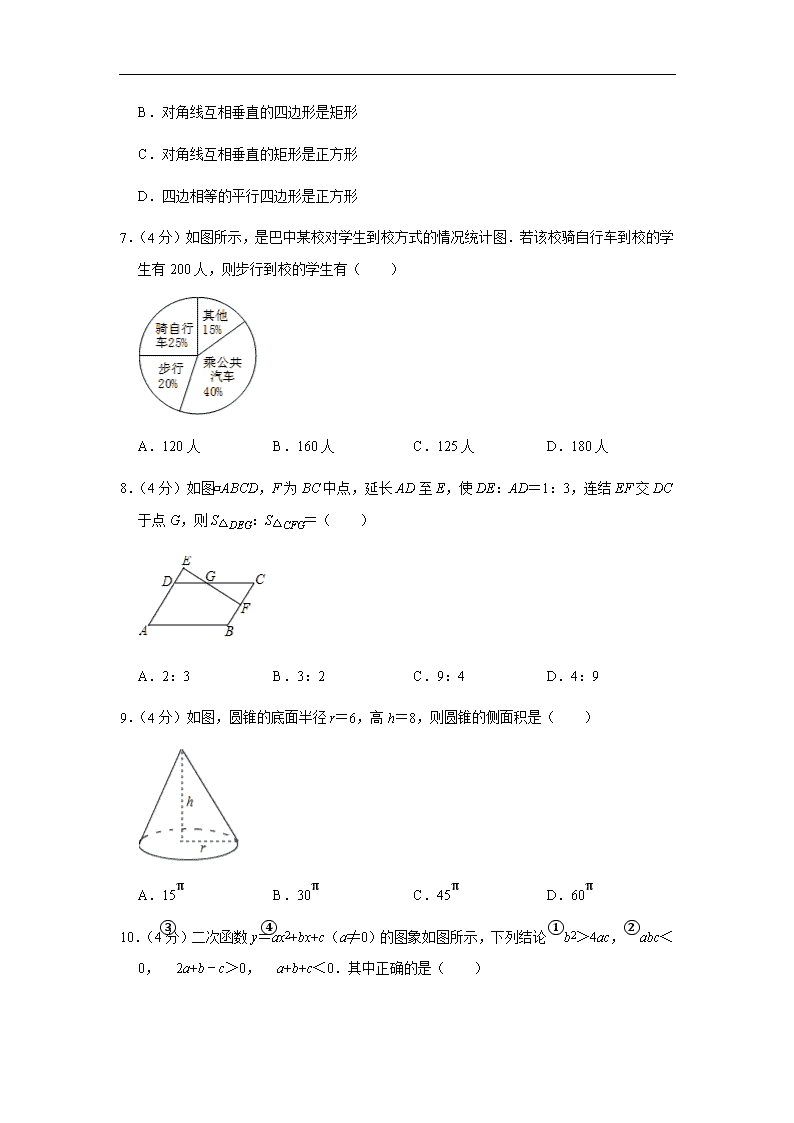7．（4分）如图所示，是巴中某校对学生到校方式的情况统计图．若该校骑自行车到校的学生有200人，则步行到校的学生有（　　）‎ A．120人 B．160人 C．125人 D．180人 ‎8．（4分）如图▱ABCD，F为BC中点，延长AD至E，使DE：AD＝1：3，连结EF交DC于点G，则S△DEG：S△CFG＝（　　）‎ A．2：3 B．3：2 C．9：4 D．4：9‎ ‎9．（4分）如图，圆锥的底面半径r＝6，高h＝8，则圆锥的侧面积是（　　）‎ A．15π B．30π C．45π D．60π ‎10．（4分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论①b2＞4ac，②abc＜0，③2a+b﹣c＞0，④a+b+c＜0．其中正确的是（　　）‎ A．①④ B．②④ C．②③ D．①②③④‎ 二、填空题（本大题共5个小题，每小题4分，共20分，将正确答案直接写在答题卡相应的位置上。）‎ ‎11．（4分）函数y‎=‎x-1‎x-3‎的自变量x的取值范围　 　．‎ ‎12．（4分）如果一组数据为4、a、5、3、8，其平均数为a，那么这组数据的方差为　 　．‎ ‎13．（4分）如图，反比例函数y‎=‎kx（x＞0）经过A、B两点，过点A作AC⊥y轴于点C，过点B作BD⊥y轴于点D，过点B作BE⊥x轴于点E，连结AD，已知AC＝1、BE＝1、S矩形BDOE＝4．则S△ACD＝　 　．‎ ‎14．（4分）若关于x的分式方程xx-2‎‎+‎2m‎2-x=‎2m有增根，则m的值为　 　．‎ ‎15．（4分）如图，等边三角形ABC内有一点P，分別连结AP、BP、CP，若AP＝6，BP＝8，CP＝10．则S△ABP+S△BPC＝　 　．‎ 三、解答题（本大题共11个小题，共90分。请把解答过程写在答题卡相应的位置上）‎ ‎16．（5分）计算（‎-‎‎1‎‎2‎）2+（3﹣π）0+|‎3‎‎-‎2|+2sin60°‎-‎‎8‎．‎ ‎17．（5分）已知实数x、y满足x-3‎‎+‎y2﹣4y+4＝0，求代数式x‎2‎‎-‎y‎2‎xy•‎1‎x‎2‎‎-2xy+‎y‎2‎‎÷‎xx‎2‎y-xy‎2‎的值．‎ ‎18．（8分）如图，等腰直角三角板如图放置．直角顶点C在直线m上，分别过点A、B作AE⊥直线m于点E，BD⊥直线m于点D．‎ ‎①求证：EC＝BD；‎ ‎②若设△AEC三边分别为a、b、c，利用此图证明勾股定理．‎ ‎19．（8分）△ABC在边长为l的正方形网格中如图所示．‎ ‎①以点C为位似中心，作出△ABC的位似图形△A1B1C，使其位似比为1：2．且△A1B1C位于点C的异侧，并表示出A1的坐标．‎ ‎②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C．‎ ‎③在②的条件下求出点B经过的路径长．‎ ‎20．（8分）在“扶贫攻坚”活动中，某单位计划选购甲、乙两种物品慰问贫困户．已知甲物品的单价比乙物品的单价高10元，若用500元单独购买甲物品与450元单独购买乙物品的数量相同．‎ ‎①请问甲、乙两种物品的单价各为多少？‎ ‎②如果该单位计划购买甲、乙两种物品共55件，总费用不少于5000元且不超过5050元，通过计算得出共有几种选购方案？‎ ‎21．（10分）如图表示的是某班部分同学衣服上口袋的数目．‎ ‎①从图中给出的信息得到学生衣服上口袋数目的中位数为　 　，众数为　 　．‎ ‎②根据如图信息，在给出的图表中绘制频数条形统计图，由此估计该班学生衣服上口袋数目为5≤x＜7的概率．‎ ‎22．（8分）已知关于x的一元二次方程x2+（2m+1）x+m2﹣1＝0有两不相等的实数根．‎ ‎①求m的取值范围．‎ ‎②设x1，x2是方程的两根且x12+x22+x1x2﹣17＝0，求m的值．‎ ‎23．（8分）某区域平面示意图如图所示，点D在河的右侧，红军路AB与某桥BC互相垂直．某校“数学兴趣小组”在“研学旅行”活动中，在C处测得点D 位于西北方向，又在A处测得点D位于南偏东65°方向，另测得BC＝414m，AB＝300m，求出点D到AB的距离．‎ ‎（参考数据sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）‎ ‎24．（8分）如图，一次函数y1＝k1x+b（k1、b为常数，k1≠0）的图象与反比例函数y2‎=‎k‎2‎x（k2≠0，x＞0）的图象交于点A（m，8）与点B（4，2）．‎ ‎①求一次函数与反比例函数的解析式．‎ ‎②根据图象说明，当x为何值时，k1x+b‎-k‎2‎x＜‎0．‎ ‎25．（10分）如图，在菱形ABCD中，连结BD、AC交于点O，过点O作OH⊥BC于点H，以点O为圆心，OH为半径的半圆交AC于点M．‎ ‎①求证：DC是⊙O的切线．‎ ‎②若AC＝4MC且AC＝8，求图中阴影部分的面积．‎ ‎③在②的条件下，P是线段BD上的一动点，当PD为何值时，PH+PM的值最小，并求出最小值．‎ ‎26．（12分）如图，抛物线y＝ax2+bx﹣5（a≠0）经过x轴上的点A（1，0）和点B及y轴上的点C，经过B、C两点的直线为y＝x+n．‎ ‎①求抛物线的解析式．‎ ‎②点P从A出发，在线段AB上以每秒1个单位的速度向B运动，同时点E从B出发，在线段BC上以每秒2个单位的速度向C运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t秒，求t为何值时，△PBE的面积最大并求出最大值．‎ ‎③过点A作AM⊥BC于点M，过抛物线上一动点N（不与点B、C重合）作直线AM的平行线交直线BC于点Q．若点A、M、N、Q为顶点的四边形是平行四边形，求点N的横坐标．‎ ‎2019年四川省巴中市中考数学试卷 参考答案与试题解析 一、选择题（本大题共10个小题，每小题4分，共40分，在每小题给出的四个选项中，只有一个选项是正确的，请使用2B铅笔将答題卡上对应题号的答案标号涂黑。）‎ ‎1．（4分）下列四个算式中，正确的是（　　）‎ A．a+a＝2a B．a5÷a4＝2a C．（a5）4＝a9 D．a5﹣a4＝a ‎【解答】解：A、a+a＝2a，故本选项正确；‎ B、a5÷a4＝a，故本选项错误；‎ C、（a5）4＝a20，故本选项错误；‎ D、a5﹣a4，不能合并，故本选项错误．‎ 故选：A．‎ ‎2．（4分）在平面直角坐标系中，已知点A（﹣4，3）与点B关于原点对称，则点B的坐标为（　　）‎ A．（﹣4，﹣3） B．（4，3） C．（4，﹣3） D．（﹣4，3）‎ ‎【解答】解：∵点A（﹣4，3），点A与点B关于原点对称，‎ ‎∴点B（4，﹣3）．‎ 故选：C．‎ ‎3．（4分）企业家陈某，在家乡投资9300万元，建立产业园区2万余亩．将9300万元用科学记数法表示为（　　）‎ A．93×108元 B．9.3×108元 C．9.3×107元 D．0.93×108元 ‎【解答】解：将9300万元用科学记数法表示为：9.3×107元．‎ 故选：C．‎ ‎4．（4分）如图是由一些小立方体与圆锥组合成的立体图形，它的主视图是（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：如图所示，它的主视图是：．‎ 故选：C．‎ ‎5．（4分）已知关于x、y的二元一次方程组ax-y=4‎‎3x+by=4‎的解是x=2‎y=-2‎，则a+b的值是（　　）‎ A．1 B．2 C．﹣1 D．0‎ ‎【解答】解：将x=2‎y=-2‎代入ax-y=4‎‎3x+by=4‎得：‎ a=1‎b=1‎‎，‎ ‎∴a+b＝2；‎ 故选：B．‎ ‎6．（4分）下列命题是真命题的是（　　）‎ A．对角线相等的四边形是矩形 ‎ B．对角线互相垂直的四边形是矩形 ‎ C．对角线互相垂直的矩形是正方形 ‎ D．四边相等的平行四边形是正方形 ‎【解答】解：A、对角线相等的平行四边形是矩形，所以A选项错误；‎ B、对角线相等的平行四边形是矩形，所以B选项错误；‎ C、对角线互相垂直的矩形是正方形，所以C选项正确；‎ D、四边相等的菱形是正方形，所以D选项错误．‎ 故选：C．‎ ‎7．（4分）如图所示，是巴中某校对学生到校方式的情况统计图．若该校骑自行车到校的学生有200人，则步行到校的学生有（　　）‎ A．120人 B．160人 C．125人 D．180人 ‎【解答】解：学生总数：200÷25%＝800（人），‎ 步行到校的学生：800×20%＝160（人），‎ 故选：B．‎ ‎8．（4分）如图▱ABCD，F为BC中点，延长AD至E，使DE：AD＝1：3，连结EF交DC于点G，则S△DEG：S△CFG＝（　　）‎ A．2：3 B．3：2 C．9：4 D．4：9‎ ‎【解答】解：设DE＝x，‎ ‎∵DE：AD＝1：3，‎ ‎∴AD＝3x，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，BC＝AD＝3x，‎ ‎∵点F是BC的中点，‎ ‎∴CF‎=‎‎1‎‎2‎BC‎=‎‎3‎‎2‎x，‎ ‎∵AD∥BC，‎ ‎∴△DEG∽△CFG，‎ ‎∴S‎△DEGS‎△CFG‎=‎（DECF）2＝（x‎3‎‎2‎x）2‎=‎‎4‎‎9‎，‎ 故选：D．‎ ‎9．（4分）如图，圆锥的底面半径r＝6，高h＝8，则圆锥的侧面积是（　　）‎ A．15π B．30π C．45π D．60π ‎【解答】解：圆锥的母线l‎=h‎2‎‎+‎r‎2‎=‎6‎‎2‎‎+‎‎8‎‎2‎=‎10，‎ ‎∴圆锥的侧面积＝π•10•6＝60π，‎ 故选：D．‎ ‎10．（4分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论①b2＞4ac，②abc＜0，③2a+b﹣c＞0，④a+b+c＜0．其中正确的是（　　）‎ A．①④ B．②④ C．②③ D．①②③④‎ ‎【解答】解：①∵抛物线与x轴由两个交点，‎ ‎∴b2﹣4ac＞0，‎ 即b2＞4ac，‎ 所以①正确；‎ ‎②由二次函数图象可知，‎ a＜0，b＜0，c＞0，‎ ‎∴abc＞0，‎ 故②错误；‎ ‎③∵对称轴：直线x‎=-b‎2a=-‎1，‎ ‎∴b＝2a，‎ ‎∴2a+b﹣c＝4a﹣c，‎ ‎∵a＜0，4a＜0，‎ c＞0，﹣c＜0，‎ ‎∴2a+b﹣c＝4a﹣c＜0，‎ 故③错误；‎ ‎④∵对称轴为直线x＝﹣1，抛物线与x轴一个交点﹣3＜x1＜﹣2，‎ ‎∴抛物线与x轴另一个交点0＜x2＜1，‎ 当x＝1时，y＝a+b+c＜0，‎ 故④正确．‎ 故选：A．‎ 二、填空题（本大题共5个小题，每小题4分，共20分，将正确答案直接写在答题卡相应的位置上。）‎ ‎11．（4分）函数y‎=‎x-1‎x-3‎的自变量x的取值范围　x≥1，且x≠3　．‎ ‎【解答】解：根据题意得：‎x-1≥0‎x-3≠0‎ 解得x≥1，且x≠3，‎ 即：自变量x取值范围是x≥1，且x≠3．‎ ‎12．（4分）如果一组数据为4、a、5、3、8，其平均数为a，那么这组数据的方差为　‎14‎‎5‎　．‎ ‎【解答】解：根据题意，得：‎4+a+5+3+8‎‎5‎‎=‎a，‎ 解得：a＝5，‎ 则这组数据为4、5、5、3、8，其平均数是5，‎ 所以这组数据的方差为‎1‎‎5‎‎×‎[（4﹣5）2+（5﹣5）2+（5﹣5）2+（3﹣5）2+（8﹣5）2]‎=‎‎14‎‎5‎，‎ 故答案为：‎14‎‎5‎．‎ ‎13．（4分）如图，反比例函数y‎=‎kx（x＞0）经过A、B两点，过点A作AC⊥y轴于点C，过点B作BD⊥y轴于点D，过点B作BE⊥x轴于点E，连结AD，已知AC＝1、BE＝1、S矩形BDOE＝4．则S△ACD＝　‎3‎‎2‎　．‎ ‎【解答】解：过点A作AH⊥x轴于点H，交BD于点F，则四边形ACOH和四边形ACDF均为矩形，如图：‎ ‎∵S矩形BDOE＝4，反比例函数y‎=‎kx（x＞0）经过B点 ‎∴k＝4‎ ‎∴S矩形ACOH＝4，‎ ‎∵AC＝1‎ ‎∴OC＝4÷1＝4‎ ‎∴CD＝OC﹣OD＝OC﹣BE＝4﹣1＝3‎ ‎∴S矩形ACDF＝1×3＝3‎ ‎∴S△ACD‎=‎‎3‎‎2‎ 故答案为：‎3‎‎2‎．‎ ‎14．（4分）若关于x的分式方程xx-2‎‎+‎2m‎2-x=‎2m有增根，则m的值为　1　．‎ ‎【解答】解：方程两边都乘x﹣2，得x﹣2m＝2m（x﹣2）‎ ‎∵原方程有增根，‎ ‎∴最简公分母x﹣2＝0，‎ 解得x＝2，‎ 当x＝2时，m＝1‎ 故m的值是1，‎ 故答案为1‎ ‎15．（4分）如图，等边三角形ABC内有一点P，分別连结AP、BP、CP，若AP＝6，BP＝8，CP＝10．则S△ABP+S△BPC＝　24+16‎3‎　．‎ ‎【解答】解：如图，将△BPC绕点B逆时针旋转60°后得△AP'B，连接PP′，‎ 根据旋转的性质可知，‎ 旋转角∠PBP′＝∠CAB＝60°，BP＝BP′，‎ ‎∴△BPP′为等边三角形，‎ ‎∴BP′＝BP＝8＝PP'；‎ 由旋转的性质可知，AP′＝PC＝10，‎ 在△BPP′中，PP′＝8，AP＝6，‎ 由勾股定理的逆定理得，△APP′是直角三角形，‎ ‎∴S△ABP+S△BPC＝S四边形AP'BP＝S△BP'B+S△AP'P‎=‎‎3‎‎4‎BP2‎+‎1‎‎2‎×‎PP'×AP＝24+16‎‎3‎ 故答案为：24+16‎‎3‎ 三、解答题（本大题共11个小题，共90分。请把解答过程写在答题卡相应的位置上）‎ ‎16．（5分）计算（‎-‎‎1‎‎2‎）2+（3﹣π）0+|‎3‎‎-‎2|+2sin60°‎-‎‎8‎．‎ ‎【解答】解：原式‎=‎1‎‎4‎+1+2-‎3‎+2×‎3‎‎2‎-2‎2‎=‎13‎‎4‎-2‎‎2‎．‎ ‎17．（5分）已知实数x、y满足x-3‎‎+‎y2﹣4y+4＝0，求代数式x‎2‎‎-‎y‎2‎xy•‎1‎x‎2‎‎-2xy+‎y‎2‎‎÷‎xx‎2‎y-xy‎2‎的值．‎ ‎【解答】解：x‎2‎‎-‎y‎2‎xy•‎‎1‎x‎2‎‎-2xy+‎y‎2‎‎÷‎xx‎2‎y-xy‎2‎ ‎=‎‎(x+y)(x-y)‎xy‎•‎1‎‎(x-y‎)‎‎2‎•xy(x-y)‎x ‎ ‎=‎x+yx‎，‎ ‎∵x-3‎‎+‎y2﹣4y+4＝0，‎ ‎∴x-3‎‎+‎（y﹣2）2＝0，‎ ‎∴x＝3，y＝2，‎ ‎∴原式‎=‎3+2‎‎3‎=‎‎5‎‎3‎．‎ ‎18．（8分）如图，等腰直角三角板如图放置．直角顶点C在直线m上，分别过点A、B作AE⊥直线m于点E，BD⊥直线m于点D．‎ ‎①求证：EC＝BD；‎ ‎②若设△AEC三边分别为a、b、c，利用此图证明勾股定理．‎ ‎【解答】①证明：∵∠ACB＝90°，‎ ‎∴∠ACE+∠BCD＝90°．‎ ‎∵∠ACE+∠CAE＝90°，‎ ‎∴∠CAE＝∠BCD．‎ 在△AEC与△BCD中，‎ ‎∠CEA=∠BDC‎∠CAE=∠BCDAC=CB‎ ‎ ‎∴△CAE≌△BCD（AAS）．‎ ‎∴EC＝BD；‎ ‎②解：由①知：BD＝CE＝a CD＝AE＝b ‎∴S梯形AEDB‎=‎‎1‎‎2‎（a+b）（a+b）‎ ‎=‎‎1‎‎2‎a2+ab‎+‎‎1‎‎2‎b2．‎ 又∵S梯形AEDB＝S△AEC+S△BCD+S△ABC ‎=‎‎1‎‎2‎ab‎+‎‎1‎‎2‎ab‎+‎‎1‎‎2‎c2‎ ‎＝ab‎+‎‎1‎‎2‎c2．‎ ‎∴‎1‎‎2‎a2+ab‎+‎‎1‎‎2‎b2＝ab‎+‎‎1‎‎2‎c2．‎ 整理，得a2+b2＝c2．‎ ‎19．（8分）△ABC在边长为l的正方形网格中如图所示．‎ ‎①以点C为位似中心，作出△ABC的位似图形△A1B1C，使其位似比为1：2．且△A1B1C位于点C的异侧，并表示出A1的坐标．‎ ‎②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C．‎ ‎③在②的条件下求出点B经过的路径长．‎ ‎【解答】解：①如图，△A1B1C为所作，点A1的坐标为（3，﹣3）；‎ ‎②如图，△A2B2C为所作；‎ ‎③OB‎=‎1‎‎2‎‎+‎‎4‎‎2‎=‎‎17‎，‎ 点B经过的路径长‎=‎90⋅π⋅‎‎17‎‎180‎=‎‎17‎‎2‎π．‎ ‎20．（8分）在“扶贫攻坚”活动中，某单位计划选购甲、乙两种物品慰问贫困户．已知甲物品的单价比乙物品的单价高10元，若用500元单独购买甲物品与450元单独购买乙物品的数量相同．‎ ‎①请问甲、乙两种物品的单价各为多少？‎ ‎②如果该单位计划购买甲、乙两种物品共55件，总费用不少于5000元且不超过5050元，通过计算得出共有几种选购方案？‎ ‎【解答】解：①设乙种物品单价为x元，则甲种物品单价为（x+10）元，由题意得：‎ ‎500‎x+10‎‎=‎‎450‎x‎ ‎ 解得x＝90‎ 经检验，x＝90符合题意 ‎∴甲种物品的单价为100元，乙种物品的单价为90元．‎ ‎②设购买甲种物品y件，则乙种物品购进（55﹣y）件 由题意得：5000≤100y+90（55﹣y）≤5050‎ 解得5≤y≤10‎ ‎∴共有6种选购方案．‎ ‎21．（10分）如图表示的是某班部分同学衣服上口袋的数目．‎ ‎①从图中给出的信息得到学生衣服上口袋数目的中位数为　4　，众数为　4　．‎ ‎②根据如图信息，在给出的图表中绘制频数条形统计图，由此估计该班学生衣服上口袋数目为5≤x＜7的概率．‎ ‎【解答】解：①由图可知，学生衣服上口袋的数目分别为：‎ ‎3，4，2，6，5，5，3，1，4，2，4，6，10，7，1，4，5，6，2，10，3．‎ 按从小到大的顺序排列为：‎ ‎1，1，2，2，2，‎ ‎3，3，3，4，4，‎ ‎4，4，5，5，5，‎ ‎6，6，6，7，10，10．‎ 故中位数为4，众数为4，‎ 故答案为4，4．‎ ‎（2）条形图如图所示：‎ 估计该班学生衣服上口袋数目为5≤x＜7的概率‎=‎6‎‎21‎=‎‎2‎‎7‎．‎ ‎22．（8分）已知关于x的一元二次方程x2+（2m+1）x+m2﹣1＝0有两不相等的实数根．‎ ‎①求m的取值范围．‎ ‎②设x1，x2是方程的两根且x12+x22+x1x2﹣17＝0，求m的值．‎ ‎【解答】解：①根据题意得：‎ ‎△＝（2m+1）2﹣4（m2﹣1）＞0，‎ 解得：m‎＞-‎‎5‎‎4‎，‎ ‎②根据题意得：‎ x1+x2＝﹣（2m+1），x1x2＝m2﹣1，‎ x12+x22+x1x2﹣17‎ ‎=‎(x‎1‎‎+x‎2‎‎)‎‎2‎-‎x1x2﹣17‎ ‎＝（2m+1）2﹣（m2﹣1）﹣17‎ ‎＝0，‎ 解得：m1‎=‎‎5‎‎3‎，m2＝﹣3（不合题意，舍去），‎ ‎∴m的值为‎5‎‎3‎．‎ ‎23．（8分）某区域平面示意图如图所示，点D在河的右侧，红军路AB与某桥BC互相垂直．某校“数学兴趣小组”在“研学旅行”活动中，在C处测得点D位于西北方向，又在A处测得点D位于南偏东65°方向，另测得BC＝414m，AB＝300m，求出点D到AB的距离．‎ ‎（参考数据sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）‎ ‎【解答】解：如图，过点D作DE⊥AB于E，过D作DF⊥BC于F，则四边形EBFD是矩形，‎ 设DE＝x，‎ 在Rt△ADE中，∠AED＝90°，‎ ‎∵tan∠DAE‎=‎DEAE，‎ ‎∴AE‎=DEtan∠DAE=‎x‎2.14‎，‎ ‎∴BE＝300‎-‎x‎2.14‎，‎ 又BF＝DE＝x，‎ ‎∴CF＝414﹣x，‎ 在Rt△CDF中，∠DFC＝90°，∠DCF＝45°，‎ ‎∴DF＝CF＝414﹣x，‎ 又BE＝CF，‎ 即：300‎-x‎2.14‎=‎414﹣x，‎ 解得：x＝214，‎ 故：点D到AB的距离是214m．‎ ‎24．（8分）如图，一次函数y1＝k1x+b（k1、b为常数，k1≠0）的图象与反比例函数y2‎=‎k‎2‎x（k2≠0，x＞0）的图象交于点A（m，8）与点B（4，2）．‎ ‎①求一次函数与反比例函数的解析式．‎ ‎②根据图象说明，当x为何值时，k1x+b‎-k‎2‎x＜‎0．‎ ‎【解答】解：①把点B（4，2）代入反比例函数y2‎=‎k‎2‎x（k2≠0，x＞0）得，k2＝4×2＝8，‎ ‎∴反比例函数的解析式为y2‎=‎‎8‎x，‎ 将点A（m，8）代入y2得，8‎=‎‎8‎m，解得m＝1，‎ ‎∴A（1，8），‎ 将A、B的坐标代入y1＝k1x+b（k1、b为常数，k1≠0）得k‎1‎‎+b=8‎‎4k‎1‎+b=2‎，‎ 解得k‎1‎‎=-2‎b=10‎，‎ ‎∴一次函数的解析式为y1＝﹣2x+10；‎ ‎②由图象可知：当0＜x＜1或x＞4时，y1＜y2，即k1x+b‎-k‎2‎x＜‎0．‎ ‎25．（10分）如图，在菱形ABCD中，连结BD、AC交于点O，过点O作OH⊥BC于点H，以点O为圆心，OH为半径的半圆交AC于点M．‎ ‎①求证：DC是⊙O的切线．‎ ‎②若AC＝4MC且AC＝8，求图中阴影部分的面积．‎ ‎③在②的条件下，P是线段BD上的一动点，当PD为何值时，PH+PM的值最小，并求出最小值．‎ ‎【解答】解：①过点O作OG⊥CD，垂足为G，‎ 在菱形ABCD中，AC是对角线，则AC平分∠BCD，‎ ‎∵OH⊥BC，OG⊥CD，‎ ‎∴OH＝OG，‎ ‎∴OH、OG都为圆的半径，即DC是⊙O的切线；‎ ‎②∵AC＝4MC且AC＝8，‎ ‎∴OC＝2MC＝4，‎ MC＝OM＝2，‎ ‎∴OH＝2，‎ 在直角三角形OHC中，HO‎=‎‎1‎‎2‎CO，‎ ‎∴∠OCH＝30°，∠COH＝60°，‎ ‎∴HC‎=CO‎2‎-OH‎2‎=2‎‎3‎，‎ S阴影＝S△OCH﹣S扇形OHM‎=‎‎1‎‎2‎CH•OH‎-‎60‎‎360‎π⋅‎OH2＝2‎3‎‎-‎‎2π‎3‎；‎ ‎③作M关于BD的对称点N，连接HN交BD于点P，‎ ‎∵PM＝NP，‎ ‎∴PH+PM＝PH+PN＝HN，此时PH+PM最小，‎ ‎∵ON＝OM＝OH，‎ ‎∠MOH＝60°，‎ ‎∴∠MNH＝30°，‎ ‎∴∠MNH＝∠HCM，‎ ‎∴HN＝HC＝2‎3‎，‎ 即：PH+PM的最小值为2‎3‎，‎ 在Rt△NPO中，‎ OP＝ONtan30°‎=‎‎2‎‎3‎‎3‎，‎ 在Rt△COD中，‎ OD＝OCtan30°‎=‎‎4‎‎3‎‎3‎，‎ 则PD＝OP+OD＝2‎3‎．‎ ‎26．（12分）如图，抛物线y＝ax2+bx﹣5（a≠0）经过x轴上的点A（1，0）和点B及y轴上的点C，经过B、C两点的直线为y＝x+n．‎ ‎①求抛物线的解析式．‎ ‎②点P从A出发，在线段AB上以每秒1个单位的速度向B运动，同时点E从B出发，在线段BC上以每秒2个单位的速度向C运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t秒，求t为何值时，△PBE的面积最大并求出最大值．‎ ‎③过点A作AM⊥BC于点M，过抛物线上一动点N（不与点B、C重合）作直线AM的平行线交直线BC于点Q．若点A、M、N、Q为顶点的四边形是平行四边形，求点N的横坐标．‎ ‎【解答】解：①∵点B、C在直线为y＝x+n上，‎ ‎∴B（﹣n，0）、C（0，n），‎ ‎∵点A（1，0）在抛物线上，‎ ‎∴a+b-5=0‎an‎2‎+bn-5=0‎n=-5‎，‎ ‎∴a＝﹣1，b＝6，‎ ‎∴抛物线解析式：y＝﹣x2+6x﹣5；‎ ‎②由题意，得，‎ PB＝4﹣t，BE＝2t，‎ 由①知，∠OBC＝45°，‎ ‎∴点P到BC的高h为BPsin45°‎=‎‎2‎‎2‎（4﹣t），‎ ‎∴S△PBE‎=‎‎1‎‎2‎BE•h‎=‎1‎‎2‎×‎2‎‎2‎(4-t)×2t=‎2‎‎2‎(t-2‎)‎‎2‎+2‎‎2‎，‎ 当t＝2时，△PBE的面积最大，最大值为2‎2‎；‎ ‎③由①知，BC所在直线为：y＝x﹣5，‎ ‎∴点A到直线BC的距离d＝2‎2‎，‎ 过点N作x轴的垂线交直线BC于点P，交x轴于点H．‎ 设N（m，﹣m2+6m﹣5），则H（m，0）、P（m，m﹣5），‎ 易证△PQN为等腰直角三角形，即NQ＝PQ＝2‎2‎，‎ ‎∴PN＝4，‎ Ⅰ．NH+HP＝4，‎ ‎∴﹣m2+6m﹣5﹣（m﹣5）＝4‎ 解得m1＝1，m2＝4，‎ ‎∵点A、M、N、Q为顶点的四边形是平行四边形，‎ ‎∴m＝4；‎ Ⅱ．NH+HP＝4，‎ ‎∴m﹣5﹣（﹣m2+6m﹣5）＝4‎ 解得m1‎=‎‎5+‎‎41‎‎2‎，m2‎=‎‎5-‎‎41‎‎2‎，‎ ‎∵点A、M、N、Q为顶点的四边形是平行四边形，‎ m＞5，‎ ‎∴m‎=‎‎5+‎‎41‎‎2‎，‎ Ⅲ．NH﹣HP＝4，‎ ‎∴﹣（﹣m2+6m﹣5）﹣[﹣（m﹣5）]＝4，‎ 解得m1‎=‎‎5+‎‎41‎‎2‎，m2‎=‎‎5-‎‎41‎‎2‎，‎ ‎∵点A、M、N、Q为顶点的四边形是平行四边形，‎ m＜0，‎ ‎∴m‎=‎‎5-‎‎41‎‎2‎，‎ 综上所述，若点A、M、N、Q为顶点的四边形是平行四边形，点N的横坐标为：4或‎5+‎‎41‎‎2‎或‎5-‎‎41‎‎2‎．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 10:01:37；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎