2020年甘肃省天水市中考数学试卷【含答案】 11页

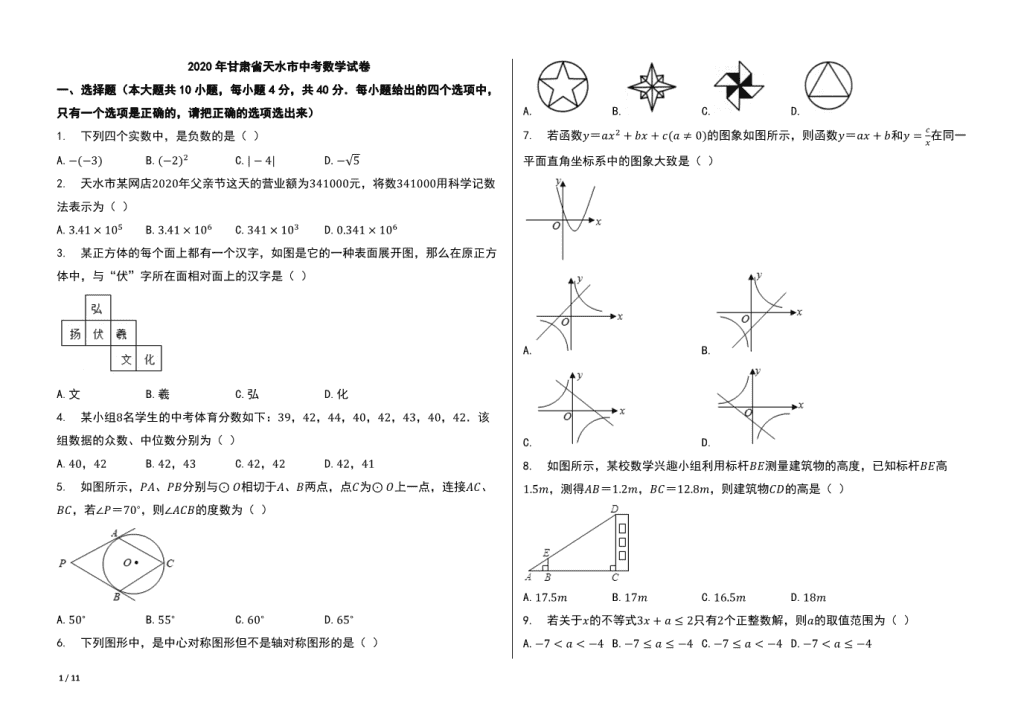
1 / 11 2020 年甘肃省天水市中考数学试卷 一、选择题（本大题共 10 小题，每小题 4 分，共 40 分．每小题给出的四个选项中， 只有一个选项是正确的，请把正确的选项选出来） 1. 下列四个实数中，是负数的是（ ） A.−(−3) B.(−2)2 C.| − 4| D.−√5 2. 天水市某网店2020年父亲节这天的营业额为341000元，将数341000用科学记数 法表示为（ ） A.3.41 × 105 B.3.41 × 106 C.341 × 103 D.0.341 × 106 3. 某正方体的每个面上都有一个汉字，如图是它的一种表面展开图，那么在原正方 体中，与“伏”字所在面相对面上的汉字是（ ） A.文 B.羲 C.弘 D.化 4. 某小组8名学生的中考体育分数如下：39，42，44，40，42，43，40，42．该 组数据的众数、中位数分别为（ ） A.40，42 B.42，43 C.42，42 D.42，41 5. 如图所示，푃퐴、푃퐵分别与⊙ 푂相切于퐴、퐵两点，点퐶为⊙ 푂上一点，连接퐴퐶、 퐵퐶，若∠푃＝70∘，则∠퐴퐶퐵的度数为（ ） A.50∘ B.55∘ C.60∘ D.65∘ 6. 下列图形中，是中心对称图形但不是轴对称图形的是（ ） A. B. C. D. 7. 若函数푦＝푎푥2 + 푏푥 + 푐(푎 ≠ 0)的图象如图所示，则函数푦＝푎푥 + 푏和푦 = 푐 푥 在同一 平面直角坐标系中的图象大致是（ ） A. B. C. D. 8. 如图所示，某校数学兴趣小组利用标杆퐵퐸测量建筑物的高度，已知标杆퐵퐸高 1.5푚，测得퐴퐵＝1.2푚，퐵퐶＝12.8푚，则建筑物퐶퐷的高是（ ） A.17.5푚 B.17푚 C.16.5푚 D.18푚 9. 若关于푥的不等式3푥 + 푎 ≤ 2只有2个正整数解，则푎的取值范围为（ ） A.−7 < 푎 < −4 B.−7 ≤ 푎 ≤ −4 C.−7 ≤ 푎 < −4 D.−7 < 푎 ≤ −4 2 / 11 10. 观察等式：2 + 22＝23 − 2；2 + 22 + 23＝24 − 2；2 + 22 + 23 + 24＝25 − 2；…已知按一定规律排列的一组数：2100，2101，2102，…，2199，2200，若2100＝푆， 用含푆的式子表示这组数据的和是（ ） A.2푆2 − 푆 B.2푆2 + 푆 C.2푆2 − 2푆 D.2푆2 − 2푆 − 2 二、填空题（本大题共 8 小题，每小题 4 分，共 32 分．只要求填写最后结果） 11. 分解因式：푚3푛 − 푚푛＝________． 12. 一个三角形的两边长分别为2和5，第三边长是方程푥2 − 8푥 + 12＝0的根，则该 三角形的周长为________． 13. 已知函数푦 = √푥+2 푥−3 ，则自变量푥的取值范围是________． 14. 已知푎 + 2푏 = 10 3 ，3푎 + 4푏 = 16 3 ，则푎 + 푏的值为________． 15. 如图所示，∠퐴푂퐵是放置在正方形网格中的一个角，则sin∠퐴푂퐵的值是________． 16. 如图所示，若用半径为8，圆心角为120∘的扇形围成一个圆锥的侧面（接缝忽略 不计），则这个圆锥的底面半径是________． 17. 如图，将正方形푂퐸퐹퐺放在平面直角坐标系中，푂是坐标原点，点퐸的坐标为 (2,  3)，则点퐹的坐标为________． 18. 如图，在边长为6的正方形퐴퐵퐶퐷内作∠퐸퐴퐹＝45∘，퐴퐸交퐵퐶于点퐸，퐴퐹交퐶퐷于 点퐹，连接퐸퐹，将△ 퐴퐷퐹绕点퐴顺时针旋转90∘得到△ 퐴퐵퐺．若퐷퐹＝3，则퐵퐸的长为 ________． 三、解答题（本大题共 3 小题，共 28 分．解答时写出必要的文字说明及演算过程） 19. （1）计算：4sin60∘ − |√3 − 2| + 20200 − √12 + (1 4)−1． 19. （2）先化简，再求值： 1 푎−1 − 푎−1 푎2+2푎+1 ÷ 푎−1 푎+1 ，其中푎 = √3． 3 / 11 20. 为了解天水市民对全市创建全国文明城市工作的满意程度，某中学数学兴趣小组 在某个小区内进行了调查统计．将调查结果分为不满意，一般，满意，非常满意四类， 回收、整理好全部问卷后，得到下列不完整的统计图． 请结合图中的信息，解决下列问题： （1）此次调查中接受调查的人数为________人； （2）请你补全条形统计图； （3）扇形统计图中“满意”部分的圆心角为________度； （4）该兴趣小组准备从调查结果为“不满意”的4位市民中随机选择2位进行回访， 已知这4位市民中有2位男性，2位女性．请用画树状图的方法求出选择回访的市民为 “一男一女”的概率． 21. 如图所示，一次函数푦＝푚푥 + 푛(푚 ≠ 0)的图象与反比例函数푦 = 푘 푥 (푘 ≠ 0)的图象 交于第二、四象限的点퐴(−2,  푎)和点퐵(푏, −1)，过퐴点作푥轴的垂线，垂足为点퐶，△ 퐴푂퐶的面积为4． （1）分别求出푎和푏的值； （2）结合图象直接写出푚푥 + 푛 > 푘 푥 中푥的取值范围； （3）在푦轴上取点푃，使푃퐵 − 푃퐴取得最大值时，求出点푃的坐标． 四、解答题（本大题共 50 分，解答时写出必要的演算步骤及推理过程） 22. 为了维护国家主权和海洋权力，海监部门对我国领海实现了常态化巡航管理．如 图所示，正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行，在퐴处 4 / 11 测得灯塔푃在北偏东60∘方向上，继续航行30分钟后到达퐵处，此时测得灯塔푃在北偏 东45∘方向上． （1）求∠퐴푃퐵的度数； （2）已知在灯塔푃的周围25海里内有暗礁，问海监船继续向正东方向航行是否安全？ （参考数据：√2 ≈ 1.414，√3 ≈ 1.732） 23. 如图，在△ 퐴퐵퐶中，∠퐶＝90∘，퐴퐷平分∠퐵퐴퐶交퐵퐶于点퐷，点푂在퐴퐵上，以点푂 为圆心，푂퐴为半径的圆恰好经过点퐷，分别交퐴퐶、퐴퐵于点퐸、퐹． （1）试判断直线퐵퐶与⊙ 푂的位置关系，并说明理由； （2）若퐵퐷＝2√3，퐴퐵＝6，求阴影部分的面积（结果保留휋）． 24. 性质探究 如图(1)，在等腰三角形퐴퐵퐶中，∠퐴퐶퐵＝120∘，则底边퐴퐵与腰퐴퐶的长度之比为 √3： 5 / 11 1 ． 理解运用 （1）若顶角为120∘的等腰三角形的周长为4 + 2√3，则它的面积为________； （2）如图(2)，在四边形퐸퐹퐺퐻中，퐸퐹＝퐸퐺＝퐸퐻，在边퐹퐺，퐺퐻上分别取中点푀，푁， 连接푀푁．若∠퐹퐺퐻＝120∘，퐸퐹＝20，求线段푀푁的长． 类比拓展 顶角为2훼的等腰三角形的底边与一腰的长度之比为________．（用含훼的式子表示） 25. 天水市某商店准备购进퐴、퐵两种商品，퐴种商品每件的进价比퐵种商品每件的进 价多20元，用2000元购进퐴种商品和用1200元购进퐵种商品的数量相同．商店将퐴种 商品每件的售价定为80元，퐵种商品每件的售价定为45元． （1）퐴种商品每件的进价和퐵种商品每件的进价各是多少元？ （2）商店计划用不超过1560元的资金购进퐴、퐵两种商品共40件，其中퐴种商品的数 量不低于퐵种商品数量的一半，该商店有几种进货方案？ （3）“五一”期间，商店开展优惠促销活动，决定对每件퐴种商品售价优惠푚(10 < 푚 < 20)元，퐵种商品售价不变，在（2）的条件下，请设计出푚的不同取值范围内， 销售这40件商品获得总利润最大的进货方案． 6 / 11 26. 如图所示，拋物线푦＝푎푥2 + 푏푥 + 푐(푎 ≠ 0)与푥轴交于퐴、퐵两点，与푦轴交于点퐶， 且点퐴的坐标为퐴(−2,  0)，点퐶的坐标为퐶(0,  6)，对称轴为直线푥＝1．点퐷是抛物线上 一个动点，设点퐷的横坐标为푚(1 < 푚 < 4)，连接퐴퐶，퐵퐶，퐷퐶，퐷퐵． （1）求抛物线的函数表达式； （2）当△ 퐵퐶퐷的面积等于△ 퐴푂퐶的面积的3 4 时，求푚的值； （3）在（2）的条件下，若点푀是푥轴上一动点，点푁是抛物线上一动点，试判断是否 存在这样的点푀，使得以点퐵，퐷，푀，푁为顶点的四边形是平行四边形．若存在，请 直接写出点푀的坐标；若不存在，请说明理由． 7 / 11 参考答案与试题解析 2020 年甘肃省天水市中考数学试卷 一、选择题（本大题共 10 小题，每小题 4 分，共 40 分．每小题给出的四个选项中， 只有一个选项是正确的，请把正确的选项选出来） 1.D 2.A 3.D 4.C 5.B 6.C 7.B 8.A 9.D 10.A 二、填空题（本大题共 8 小题，每小题 4 分，共 32 分．只要求填写最后结果） 11.푚푛(푚 − 1)(푚 + 1) 12.13 13.푥 ≥ −2且푥 ≠ 3 14.1 15.√2 2 16.8 3 17.(−1,  5) 18.2 三、解答题（本大题共 3 小题，共 28 分．解答时写出必要的文字说明及演算过程） 19.原式＝4 × √3 2 − (2 − √3) + 1 − 2√3 + 4 ＝2√3 − 2 + √3 + 1 − 2√3 + 4 ＝3 + √3； 原式= 1 푎−1 − 푎−1 (푎+1)2 ⋅ 푎+1 푎−1 = 1 푎 − 1 − 1 푎 + 1 = 푎 + 1 (푎 + 1)(푎 − 1) − 푎 − 1 (푎 + 1)(푎 − 1) = 2 (푎 + 1)(푎 − 1) = 2 푎2−1 ， 当푎 = √3时， 原式= 2 (√3)2−1 = 2 3 − 1 = 2 2 ＝1． 20.50 此次调查中结果为满意的人数为：50 − 4 − 8 − 18＝20（人）； 144 画树状图得： 8 / 11 ∵ 共有12种等可能的结果，选择回访市民为“一男一女”的有8种情况， ∴ 选择回访的市民为“一男一女”的概率为： 8 12 = 2 3 ． 21.∵ △ 퐴푂퐶的面积为4， ∴ 1 2 |푘|＝4， 解得，푘＝−8，或푘＝8（不符合题意舍去）， ∴ 反比例函数的关系式为푦 = − 8 푥 ， 把点퐴(−2,  푎)和点퐵(푏, −1)代入푦 = − 8 푥 得， 푎＝4，푏＝8； 答：푎＝4，푏＝8； 根据一次函数与反比例函数的图象可知，不等式푚푥 + 푛 > 푘 푥 的解集为푥 < −2或0 < 푥 < 8； ∵ 点퐴(−2,  4)关于푦轴的对称点퐴′(2,  4)， 又퐵(8, −1)，则直线퐴′퐵与푦轴的交点即为所求的点푃， 设直线퐴′퐵的关系式为푦＝푐푥 + 푑， 则有{ 2푐 + 푑 = 4 8푐 + 푑 = −1 ， 解得，{ 푐 = − 5 6 푑 = 17 3 ， ∴ 直线퐴′퐵的关系式为푦 = − 5 6 푥 + 17 3 ， ∴ 直线푦 = − 5 6 푥 + 17 3 与푦轴的交点坐标为(0, 17 3 )， 即点푃的坐标为(0, 17 3 )． 四、解答题（本大题共 50 分，解答时写出必要的演算步骤及推理过程） 22.由题意得，∠푃퐴퐵＝90∘ − 60∘＝30∘，∠퐴푃퐵＝90∘ + 45∘＝135∘， ∴ ∠퐴푃퐵＝180∘ − ∠푃퐴퐵 − ∠퐴푃퐵＝180∘ − 30∘ − 135∘＝15∘； 作푃퐻 ⊥ 퐴퐵于퐻，如图： 则△ 푃퐵퐻是等腰直角三角形， ∴ 퐵퐻＝푃퐻， 设퐵퐻＝푃퐻＝푥海里， 由题意得：퐴퐵＝40 × 30 60 = 20（海里）， 在푅푡 △ 퐴푃퐻中，tan∠푃퐴퐵＝tan30∘ = 푃퐻 퐴퐻 = √3 3 ， 即 푥 20+푥 = √3 3 ， 解得：푥＝10√3 + 10 ≈ 27.32 > 25，且符合题意， ∴ 海监船继续向正东方向航行安全． 23.证明：连接푂퐷，如图： ∵ 푂퐴＝푂퐷， ∴ ∠푂퐴퐷＝∠푂퐷퐴， ∵ 퐴퐷平分∠퐶퐴퐵， ∴ ∠푂퐴퐷＝∠퐶퐴퐷， ∴ ∠퐶퐴퐷＝∠푂퐷퐴， ∴ 퐴퐶 // 푂퐷， ∴ ∠푂퐷퐵＝∠퐶＝90∘， 即퐵퐶 ⊥ 푂퐷， 又∵ 푂퐷为⊙ 푂的半径， 9 / 11 ∴ 直线퐵퐶是⊙ 푂的切线； 设푂퐴＝푂퐷＝푟，则푂퐵＝6 − 푟， 在푅푡 △ 푂퐷퐵中，由勾股定理得：푂퐷2 + 퐵퐷2＝푂퐵2， ∴ 푟2 + (2√3)2＝(6 − 푟)2， 解得：푟＝2， ∴ 푂퐵＝4， ∴ 푂퐷 = √푂퐵2 − 퐵퐷2 = √42 − (2√3)2 = 2， ∴ 푂퐷 = 1 2 푂퐵， ∴ ∠퐵＝30∘， ∴ ∠퐷푂퐵＝180∘ − ∠퐵 − ∠푂퐷퐵＝60∘， ∴ 阴影部分的面积푆＝푆△푂퐷퐵 − 푆扇形퐷푂퐹 = 1 2 × 2 √3 × 2 − 60휋×22 360 = 2√3 − 2휋 3 ． 24.√3 2sin훼: 1 25.设퐴种商品每件的进价是푥元，则퐵种商品每件的进价是(푥 − 20)元， 由题意得：2000 푥 = 1200 푥−20 ， 解得：푥＝50， 经检验，푥＝50是原方程的解，且符合题意， 50 − 20＝30， 答：퐴种商品每件的进价是50元，퐵种商品每件的进价是30元； 设购买퐴种商品푎件，则购买퐵商品(40 − 푎)件， 由题意得：{ 50푎 + 30(40 − 푎) ≤ 1560 푎 ≥ 1 2 (40 − 푎) ， 解得40 3 ≤ 푎 ≤ 18， ∵ 푎为正整数， ∴ 푎＝14、15、16、17、18， ∴ 商店共有5种进货方案； 设销售퐴、퐵两种商品共获利푦元， 由题意得：푦＝(80 − 50 − 푚)푎 + (45 − 30)(40 − 푎)＝(15 − 푚)푎 + 600， ①当10 < 푚 < 15时，15 − 푚 > 0，푦随푎的增大而增大， ∴ 当푎＝18时，获利最大，即买18件퐴商品，22件퐵商品， ②当푚＝15时，15 − 푚＝0， 푦与푎的值无关，即（2）问中所有进货方案获利相同， ③当15 < 푚 < 20时，15 − 푚 < 0，푦随푎的增大而减小， ∴ 当푎＝14时，获利最大，即买14件퐴商品，26件퐵商品． 26.由题意得：{ − 푏 2푎 = 1 4푎 − 2푏 + 푐 = 0 푐 = 6 ， 解得：{ 푎 = − 3 4 푏 = 3 2 푐 = 6 ， ∴ 抛物线的函数表达式为：푦 = − 3 4 푥2 + 3 2 푥 + 6； 过点퐷作퐷퐸 ⊥ 푥轴于퐸，交퐵퐶于퐺，过点퐶作퐶퐹 ⊥ 퐸퐷交퐸퐷的延长线于퐹，如图1所示： ∵ 点퐴的坐标为(−2,  0)，点퐶的坐标为(0,  6)， ∴ 푂퐴＝2，푂퐶＝6， ∴ 푆△퐴푂퐶 = 1 2 푂퐴 ⋅ 푂퐶 = 1 2 × 2 × 6＝6， ∴ 푆△퐵퐶퐷 = 3 4 푆△퐴푂퐶 = 3 4 × 6 = 9 2 ， 10 / 11 当푦＝0时，− 3 4 푥2 + 3 2 푥 + 6＝0， 解得：푥1＝−2，푥2＝4， ∴ 点퐵的坐标为(4,  0)， 设直线퐵퐶的函数表达式为：푦＝푘푥 + 푛， 则{0 = 4푘 + 푛 6 = 푛 ， 解得：{푘 = − 3 2 푛 = 6 ， ∴ 直线퐵퐶的函数表达式为：푦 = − 3 2 푥 + 6， ∵ 点퐷的横坐标为푚(1 < 푚 < 4)， ∴ 点퐷的坐标为：(푚, − 3 4 푚2 + 3 2 푚 + 6)， 点퐺的坐标为：(푚, − 3 2 푚 + 6)， ∴ 퐷퐺 = − 3 4 푚2 + 3 2 푚 + 6 − (− 3 2 푚 + 6) = − 3 4 푚2 + 3푚，퐶퐹＝푚，퐵퐸＝4 − 푚， ∴ 푆△퐵퐶퐷＝푆△퐶퐷퐺 + 푆△퐵퐷퐺 = 1 2 퐷퐺 ⋅ 퐶퐹 + 1 2 퐷퐺 ⋅ 퐵퐸 = 1 2 퐷퐺 × (퐶퐹 + 퐵퐸) = 1 2 × (− 3 4 푚2 + 3푚) × (푚 + 4 − 푚) = − 3 2 푚2 + 6푚， ∴ − 3 2 푚2 + 6푚 = 9 2 ， 解得：푚1＝1（不合题意舍去），푚2＝3， ∴ 푚的值为3； 由（2）得：푚＝3，− 3 4 푚2 + 3 2 푚 + 6 = − 3 4 × 32 + 3 2 × 3 + 6 = 15 4 ， ∴ 点퐷的坐标为：(3, 15 4 )， 分三种情况讨论： ①当퐷퐵为对角线时，如图2所示： ∵ 四边形퐵푁퐷푀是平行四边形， ∴ 퐷푁 // 퐵푀， ∴ 퐷푁 // 푥轴， ∴ 点퐷与点푁关于直线푥＝1对称， ∴ 푁(−1, 15 4 )， ∴ 퐷푁＝3 − (−1)＝4， ∴ 퐵푀＝4， ∵ 퐵(4,  0)， ∴ 푀(8,  0)； ②当퐷푀为对角线时，如图3所示： 由①得：푁(−1, 15 4 )，퐷푁＝4， ∵ 四边形퐵푁퐷푀是平行四边形， ∴ 퐷푁＝퐵푀＝4， ∵ 퐵(4,  0)， ∴ 푀(0,  0)； ③当퐷푁为对角线时， ∵ 四边形퐵푁퐷푀是平行四边形， ∴ 퐷푀＝퐵푁，퐷푀 // 퐵푁， ∴ ∠퐷푀퐵＝∠푀퐵푁， ∴ 点퐷与点푁的纵坐标相等， ∵ 点퐷(3, 15 4 )， ∴ 点푁的纵坐标为：− 15 4 ， 将푦 = − 15 4 代入푦 = − 3 4 푥2 + 3 2 푥 + 6中， 得：− 3 4 푥2 + 3 2 푥 + 6 = − 15 4 ， 解得：푥1＝1 + √14，푥2＝1 − √14， 当푥＝1 + √14时，如图4所示： 则푁(1 + √14, − 15 4 )， 分别过点퐷、푁作푥轴的垂线，垂足分别为퐸、푄， 11 / 11 在푅푡 △ 퐷퐸푀和푅푡 △ 푁푄퐵中，{퐷푀 = 퐵푁 퐷퐸 = 푁푄 ， ∴ 푅푡 △ 퐷퐸푀 ≅ 푅푡 △ 푁푄퐵(퐻퐿)， ∴ 퐵푄＝퐸푀， ∵ 퐵푄＝1 + √14 − 4 = √14 − 3， ∴ 퐸푀 = √14 − 3， ∵ 퐸(3,  0)， ∴ 푀(√14, 0)； 当푥＝1 − √14时，如图5所示： 则푁(1 − √14, − 15 4 )， 同理得点푀(−√14,  0)； 综上所述，点푀的坐标为(8,  0)或(0,  0)或(√14,  0)或(−√14,  0)．