上海中考二模 徐汇数学（含答案） 8页

‎2011学年第二学期徐汇区初三年级数学教改先锋 学习能力诊断卷　 2012．4　　　　‎ ‎（时间100分钟 满分150分） ‎ 考生注意∶‎ ‎1．本试卷含三个大题，共25题；答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；‎ ‎2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】‎ ‎1．下列实数中，无理数是 ‎（A）； （B）； （C）； （D）． ‎ ‎2．下列图形中，既是轴对称图形又是中心对称图形是 ‎（A）正六边形； （B）正五边形； （C）等腰梯形； （D）等边三角形．‎ ‎3．如果，那么的值是 ‎（A） ； （B） 2； （C） 1； （D） 0．‎ ‎4．下列成语或词语所反映的事件中，可能性大小最小的是 ‎（A）瓮中捉鳖； （B）守株待兔； （C）旭日东升； （D）夕阳西下． ‎ ‎5．某商店在一周内卖出某种品牌球鞋的尺寸（单位：码）整理后的数据如下：36，38，38， 39，40，40，41，41，41，41，42，43，44．那么这组数据的中位数和众数分别为 ‎（A）40，40； （B）41，40； （C）40，41； （D）41，41．‎ ‎6．下列关于四边形是矩形的判断中，正确的是 ‎（A）对角线互相平分； （B）对角线互相垂直；‎ ‎（C）对角线互相平分且垂直； （D）对角线互相平分且相等．‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎【请将结果直接填入答题纸的相应位置上】[来源:教+改_先_锋§网]‎ ‎7．计算： ▲ ． ‎ ‎8．求值： ▲ ．‎ ‎9．函数的定义域是 ▲ ．‎ ‎10．如果方程有两个相等的实数根，那么m的值是 ▲ ．‎ ‎11．如果将抛物线向左平移2个单位，再向上平移3个单位，那么平移后的抛物线表达式是 ▲ ．‎ ‎12．纳米是一个长度单位，1纳米＝0.000 000 ‎001米，如果把水分子看成是球形，它的直径约为0.4纳米，用科学记数法表示为米，那么的值是 ▲ ．‎ ‎13．如图1，一斜坡的坡比，如果坡高米，那么它的水平宽度的长是 ▲ 米．‎ ‎14．一次函数中两个变量的部分对应值如下表所示：‎ x ‎…‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y ‎…‎ ‎8‎ ‎5‎ ‎2‎ ‎-1‎ ‎-4‎ ‎…‎ 那么关于的不等式的解集是 ▲ ．‎ ‎15．点是△ABC的重心，如果，，那么向量用向量和表示 为 ▲ ．‎ ‎16．为了了解全区近6000名初三学生数学学习状况，随机抽取600名学生的测试成绩作为样本，将他们的成绩整理后分组情况如下：（每组数据含最低值，不含最高值）‎ 分组（分）‎ ‎40～50‎ ‎50～60‎ ‎60～70‎ ‎70～80‎ ‎80～90‎ ‎90～100‎ 频数 ‎12‎ ‎18‎ ‎180‎ 频率 ‎0.16‎ ‎0.04‎ ‎[来源:J.gx.fw.Com]‎ 根据上表信息，由此样本请你估计全区此次测试成绩在70～80分的人数大约是 ▲ ．‎ ‎17．如图2，矩形中，，点分别在轴、轴的正半轴上，点在第一象限，如果，那么点的坐标是 ▲ ． ‎ ‎18．如图3，在菱形中，，,点在射线上，，如果 与射线相交于点，那么 ▲ ．‎ O B x A C D y 图2‎ A C B 图1‎ A B D C 图3‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ 化简：．‎ ‎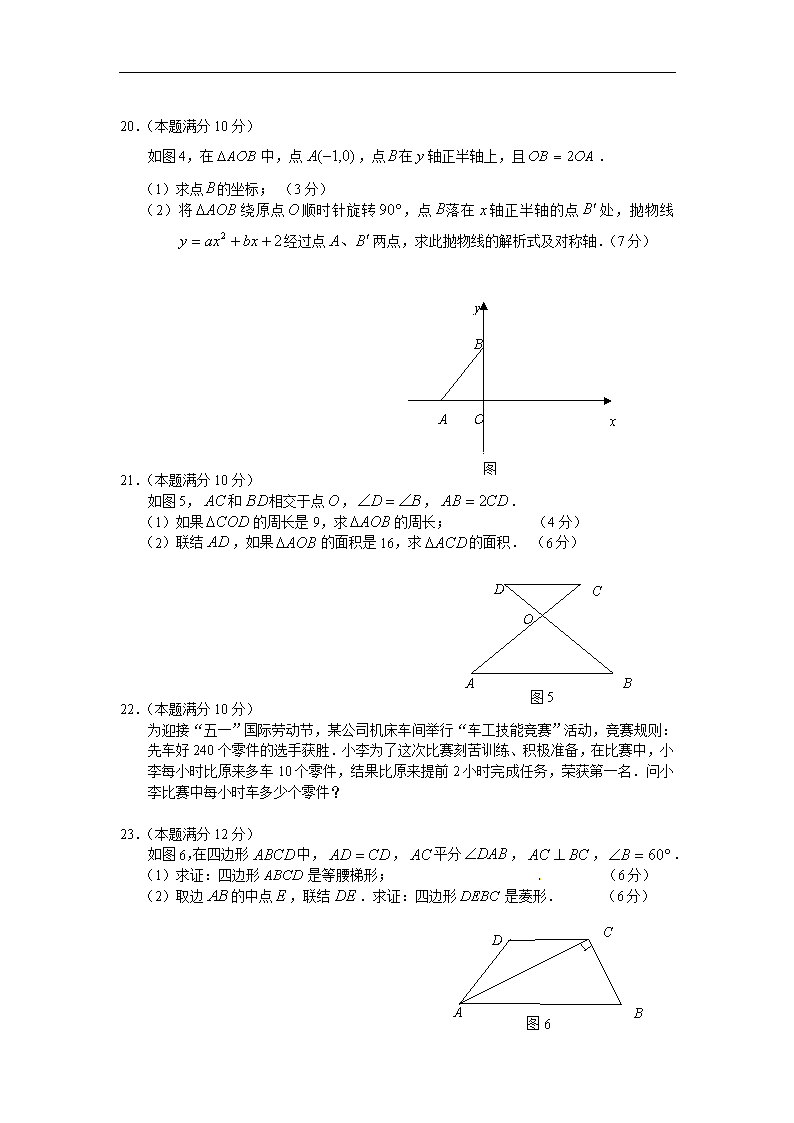20．（本题满分10分）‎ 如图4，在中，点，点在轴正半轴上，且．‎ ‎（1）求点的坐标； （3分）‎ ‎（2）将绕原点顺时针旋转，点落在轴正半轴的点处，抛物线经过点两点，求此抛物线的解析式及对称轴．（7分）‎ A O B y x 图4‎ ‎[来源:教改先锋网J.GX.FW]‎ ‎21．（本题满分10分）‎ 如图5，和相交于点，，．‎ ‎（1）如果的周长是9，求的周长； （4分）‎ ‎（2）联结，如果的面积是16，求的面积． （6分）‎ A B C D O 图5‎ ‎[来源:教|改|先锋*网]‎ ‎22．（本题满分10分）‎ 为迎接“五一”国际劳动节，某公司机床车间举行“车工技能竞赛”活动，竞赛规则：先车好240个零件的选手获胜．小李为了这次比赛刻苦训练、积极准备，在比赛中，小李每小时比原来多车10个零件，结果比原来提前2小时完成任务，荣获第一名．问小李比赛中每小时车多少个零件？‎ ‎23．（本题满分12分）‎ 如图6，在四边形中，，平分，，．‎ ‎（1）求证：四边形是等腰梯形； （6分）‎ ‎（2）取边的中点，联结．求证：四边形是菱形． （6分）‎ A B C D 图6‎ ‎24．（本题满分12分）‎ 函数和的图像关于轴对称，我们把函数和叫做互为“镜子”函数．‎ 类似地，如果函数和的图像关于轴对称，那么我们就把函数和叫做互为“镜子”函数．‎ ‎（1）请写出函数的“镜子”函数： ，（3分）‎ ‎（2）函数 的“镜子”函数是； （3分）‎ A B C O 图7‎ ‎（3）如图7，一条直线与一对“镜子”函数（＞）和（＜）的图像分别交于点，如果，点在函数（＜）的“镜子”函数上的对应点的横坐标是，求点的坐标． （6分）‎ ‎25．（本题满分14分）‎ 在中，，，，⊙的半径长为1，⊙交边 于点，点是边上的动点．‎ ‎（1）如图8，将⊙绕点旋转得到⊙，请判断⊙与直线的位置关系；‎ ‎（4分）‎ ‎（2）如图9，在（1）的条件下，当是等腰三角形时，求的长； （5分）‎ ‎（3）如图10，点是边上的动点，如果以为半径的⊙和以为半径的 ‎⊙外切，设，，求关于的函数关系式及定义域．（5分）．‎ B O A C P 图9‎ B O A C P 图8‎ 图10‎ O N B A C ‎2011学年第二学期徐汇区初三年级数学教改先锋 学习能力诊断卷参考答案和评分标准 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．C； 2．A； 3．D； 4．B； 5．D； 6．D．‎ 二．填空题：（本大题共12题，满分48分）‎ ‎7．； 8．； 9．； 10．； 11．（）； 12．；‎ ‎13．； 14．； 15．； 16．； 17．； 18．或．‎ 三、（本大题共7题，第19、20、21、22题每题10分，第23、24题每题12分，第25题14分，满分78分）‎ ‎19. 解：原式＝ ……………………………（6分）‎ ‎ ＝ ………………………………………………（2分）‎ ‎ ＝ ………………………………………………………（2分）‎ ‎20．解：（1）∵，∴……………………………………………（1分）‎ ‎∵，∴ ………………………………………（1分）‎ ‎ ∴．…………………………………………………………（1分）‎ ‎（2）由题意，得，………………………………………………（1分）‎ ‎∴ ，解得， …………………………（3分）‎ ‎∴．………………………………………………（1分）‎ 对称轴为直线．………………………………………………（2分）‎ ‎21．解：（1） ∵，；‎ ‎ ∴∽，……………………………………………（1分）‎ ‎∴ …………………………………（2分）‎ ‎∵，∴．…………………………………（1分）‎ （2） ‎∵∽，‎ ‎∴，．………………………（2分）‎ ‎∵，∴ ………………………………………（1分）‎ ‎ 设中边上的高为．‎ ‎∴，∴． ………………（2分）‎ ‎∴．……………………………………（1分）‎ ‎22．解： 设小李比赛中每小时车个零件，则小李原来每小时车个零件．（1分）‎ 由题意，得 ；………………………………………（4分）‎ 化简，得 ； ……………………………………（2分）‎ 解得， ，； ……………………………………（2分）‎ 经检验，都是原方程的根，但不合题意，舍去（1分）‎ 答： 小李比赛中每小时车个零件．‎ ‎23．证明：（1）∵，∴ ‎ ‎∵平分，∴‎ ‎∴ ，∴∥…………………………………（2分）‎ 在中，，‎ ‎∴,∴ …………………………………（1分）‎ ‎∴，∴ ………………（1分）‎ ‎∵‎ ‎∴与不平行， ………………………………………………（1分）‎ ‎∴四边形是等腰梯形． ………………………………………（1分）‎ ‎（2）∵，，∴ …………………………（1分）‎ 在中，，‎ ‎∴, …………………………………………………（1分）‎ ‎∴，∵∥……………………………………………（2分）‎ ‎∴四边形是平行四边形…………………………………………（1分）‎ ‎∵‎ ‎∴四边形是菱形．………………………………………………（1分）‎ ‎24．解：（1）；………………………………………………………………（3分）‎ ‎（2）；…………………………………………………………（3分）‎ ‎（3）分别过点作垂直于轴，垂足分别为．‎ 设点、，其中＞，＞． ………………………（1分）‎ 由题意，得 点．……………………………………………………（1分）‎ ‎∴,，，，．‎ 易知 ∥∥, 又 所以，可得 ，…………………………………………（2分）‎ 化简，得 ，解得 （负值舍去）……………（1分）‎ ‎∴， ∴…………………………（1分）‎ ‎25．解：（1）在Rt△ABC中，，∵，‎ ‎∴， ………………（1分）‎ 过点作，垂足为．……………………………………（1分）‎ 在中，，∴， ‎ ‎∵，∴＞……………………………………（1分）‎ ‎∴⊙与直线相离．…………………………………………………（1分）‎ ‎（2）分三种情况：‎ ‎ ∵＞，∴＞；……………………………（1分）‎ ‎ 当时，易得，‎ ‎ ∴，∴，∴；………（2分）‎ ‎ 当时，过点作，垂足为．[来源:教改先锋网]‎ ‎ ∴，∴，∴．………（2分） ‎ 综合，当是等腰三角形时，的长为或． ‎ ‎（3）联结，过点作，垂足为．‎ 在中，，，；‎ ‎∴，；∴，…………………（1分）‎ ‎∵⊙和⊙外切，∴；…………………………………（1分）‎ 在中，，∴；‎ 即；‎ ‎∴；…………………………………………………………（2分）‎ 定义域为：＜＜．……………:………………………………………（1分）‎