2009年广东省佛山市中考数学试题 9页

佛山市2009 年高中阶段学校招生考试 数学试卷 说　明：本试卷分为第Ι卷(选择题)和第Ⅱ卷（非选择题）两部分，共6页，满分120分，考试时间100分钟．‎ 注意事项：‎ ‎1.试卷的选择题和非选择题都在答题卡上作答，不能答在试卷上.‎ ‎2.要作图（含辅助线）或画表，先用铅笔进行画线、绘图，再用黑色字迹的钢笔或签字 笔描黑.‎ ‎3.其余注意事项，见答题卡.‎ 第Ⅰ卷（选择题 共30 分）‎ 一、选择题(本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．答案选项填涂在答题卡上)．‎ ‎1．化简的结果是(　　　) ‎ Ａ．2　　　　　Ｂ． C． D．‎ ‎2．数学上一般把记为(　　　)‎ A． B． C． D．‎ 实物图 ‎3．30°角的余角是( )‎ A．30°角 B．60°角 C．90°角 D．150°角 ‎4．在水平的讲台上放置圆柱形水杯和长方体形粉笔盒（右图），则它的主视图是( )‎ 图④‎ 图③‎ 图②‎ 图①‎ A．图① 　B．图② 　 C．图③ 　 D．图④‎ ‎5．据佛山日报报道，‎2009年6月1日佛山市最高气温是‎33℃‎，最低气温是‎24℃‎，则当天佛山市气温（℃）的变化范围是(　　　) ‎ A．　　　　B．　　　 C．　　　 D．‎ ‎6．方程的解是（　　　）‎ A．0　　　　　　 B．1　　　　　　　C．2　　　　　　 D．3‎ ‎7．下列关于数与式的等式中，正确的是(　　　)‎ A．　　　B．　　　C．　　D．‎ ‎8．假设你班有男生24名，女生26名，班主任要从班里任选一名红十字会的志愿者，则你被选中的概率是(　　　)‎ r r 第9题图 A．　　　 B．　　　C．　　　　D．‎ ‎9．将两枚同样大小的硬币放在桌上，固定其中一枚，而另一枚则沿着其边缘滚动一周，这时滚动的硬币滚动了(　　　)‎ A．1圈 　　　B．1.5圈　　　　C．2圈 　　　　D．2.5圈 ‎10．在学习掷硬币的概率时，老师说：“掷一枚质地均匀的硬币，正面朝上的概率是”，小明做了下列三个模拟实验来验证．‎ ‎①取一枚新硬币，在桌面上进行抛掷，计算正面朝上的次数与总次数的比值 ‎②把一个质地均匀的圆形转盘平均分成偶数份，并依次标上奇数和偶数，转动转盘，计算指针落在奇数区域的次数与总次数的比值 ‎③将一个圆形纸板放在水平的桌面上，纸板正中间放一个圆锥(如右图)，从圆锥的正上方往下撒米粒，计算其中一半纸板上的米粒数与纸板上总米粒数的比值 上面的实验中，不科学的有(　　　)‎ A．0个　　　B．1个 　　　C．2个 　　　　D．3个 第Ⅱ卷（非选择题 共90分）‎ 二、填空题(本大题共5小题，每小题3分，共15分．把答案填在答题卡中)．‎ ‎11．黄金分割比是=，将这个分割比用四舍五入法精确到0.001的 近似数是 　　　　　　．‎ ‎1‎ ‎1‎ O x y 第14题图 ‎12．正方形有　　　　　　　条对称轴．‎ ‎13．已知一组数据：11，15，13，12，15，15，16，15．令这组数据的众数为，中位数为，则　　　　　　（填“”、“”或“=”）．‎ ‎14．画出一次函数的图象，并回答：当函数值为正时，的取值范围是 　　　　．‎ ‎15．已知的三边分别是，两圆的半径，圆心距，则这两个圆的位置关系是　　　　　　．‎ 三、解答题（在答题卡上作答，写出必要的解题步骤．16~20题每小题6分，21～23题每小题8分，24题10分，25题11分，共75分）．‎ ‎16．化简：．‎ ‎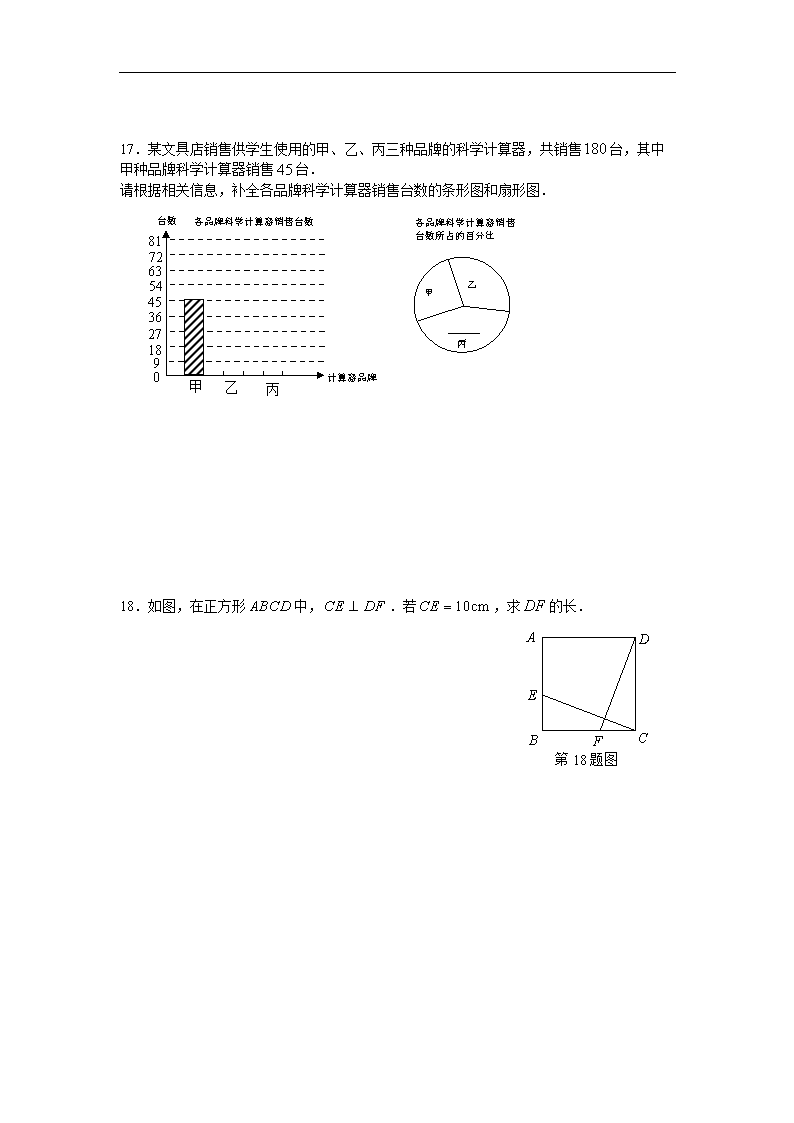17．某文具店销售供学生使用的甲、乙、丙三种品牌的科学计算器，共销售台，其中 甲种品牌科学计算器销售台．‎ 请根据相关信息，补全各品牌科学计算器销售台数的条形图和扇形图．‎ ‎0‎ ‎9‎ ‎18‎ ‎27‎ ‎36‎ ‎45‎ ‎54‎ ‎63‎ ‎72‎ ‎81‎ 甲 乙 丙 计算器品牌 台数 各品牌科学计算器销售台数 各品牌科学计算器销售台数所占的百分比 甲25%‎ 乙30%‎ 丙 ‎18．如图，在正方形中，．若，求的长．‎ D F C B E A 第18题图 ‎19．（1）请在坐标系中画出二次函数的大致图象；‎ ‎（2）在同一个坐标系中画出的图象向上平移两个单位后的图象；‎ x y O 第19题图 ‎（3）直接写出平移后的图象的解析式.‎ 注：图中小正方形网格的边长为1.‎ ‎20．（1）有这样一个问题：与下列哪些数相乘，结果是有理数？‎ A． B． C． D． E．‎ 问题的答案是（只需填字母）： ；‎ ‎（2）如果一个数与相乘的结果是有理数，则这个数的一般形式是什么（用代数式 表示）.‎ ‎21．（1）列式：与的差不小于；‎ ‎（2）若（1）中的（单位：）是一个正方形的边长，现将正方形的边长增加，‎ 则正方形的面积至少增加多少？‎ ‎22．已知，一个圆形电动砂轮的半径是，转轴长是．砂轮未工作时停靠在竖直的档板上，边缘与档板相切于点．现在要用砂轮切割水平放置的薄铁片（铁片厚度忽略不计，是切痕所在的直线）．‎ ‎（1）在图的坐标系中，求点与点的坐标；‎ ‎（2）求砂轮工作前后，转轴旋转的角度和圆心转过的弧长．‎ 第22题图①‎ 第22题图②‎ 注：图是未工作时的示意图，图是工作前后的示意图．‎ ‎23．如图，一个长方体形的木柜放在墙角处（与墙面和地面均没有缝隙），有一只蚂蚁从柜角处沿着木柜表面爬到柜角处．‎ ‎（1）请你画出蚂蚁能够最快到达目的地的可能路径；‎ ‎（2）当时，求蚂蚁爬过的最短路径的长；‎ ‎（3）求点到最短路径的距离．‎ 第23题备用图 第23题图 ‎24．阅读材料：把形如的二次三项式(或其一部分)配成完全平方式的方法叫做配方法. 配方法的基本形式是完全平方公式的逆写，即．‎ 例如：、是的三种不同形式的配方（即“余项”分别是常数项、一次项、二次项——见横线上的部分）．‎ 请根据阅读材料解决下列问题：‎ ‎（1）比照上面的例子，写出三种不同形式的配方；‎ ‎（2）将配方(至少两种形式)；‎ ‎（3）已知，求的值．‎ ‎25．一般地，学习几何要从作图开始，再观察图形，根据图形的某一类共同特征对图形进行分类（即给一类图形下定义——定义概念便于归类、交流与表达），然后继续研究图形的其它特征、判定方法以及图形的组合、图形之间的关系、图形的计算等问题. 课本里对四边形的研究即遵循着上面的思路．‎ 当然，在学习几何的不同阶段，可能研究的是几何的部分问题．比如有下面的问题，请你研究．‎ 已知：四边形中，，且．‎ ‎（1）借助网格画出四边形所有可能的形状；‎ ‎（2）简要说明在什么情况下四边形具有所画的形状．‎ 佛山市2009 年高中阶段学校招生考试 数学试卷参考答案与评分标准 一、选择题．‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B C B B D C A D C A 二、填空题．‎ 题号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答案 ‎0.618‎ ‎4‎ ‎=‎ 图略，‎ 相交 注：14题，作图正确给2分，范围正确给1分．‎ 三、解答题．‎ ‎16．解：．‎ 注：通分2分、合并1分、化乘1分、约分2分．其它作法参照给分．‎ ‎17．‎ ‎0‎ ‎9‎ ‎18‎ ‎27‎ ‎36‎ ‎45‎ ‎54‎ ‎63‎ ‎72‎ ‎81‎ 甲 乙 丙 计算器品牌 台数 各品牌科学计算器销售台数 各品牌科学计算器销售台数所占的百分比 甲25%‎ 乙25%‎ 丙 ‎45%‎ D F C B E A 第18题图 注：每处满分2 分 ‎18．解（略）．‎ 注：证明，给5分；根据三角形全等得，给1分．‎ ‎19．（1）画图（略）‎ 注：基本反映图形的特征（如顶点、对称性、变化趋势、平滑）给2分，满足其中的两至三项给1分，满足一项以下给0分；‎ ‎（2）画图、写解析式（略）‎ 注：画图满分2分，同（1）的标准；写解析式2分（无过程不扣分）．‎ ‎20．（1）；‎ 注：每填对一个得1分，每填错一个扣1分，但本小题总分最少0分．‎ ‎（2）设这个数为，则（为有理数），所以（为有理数）．‎ 注：无“为有理数”扣1分；写视同．‎ ‎21．（1）；（化为扣1分） 3分 ‎（2）面积增加．（列式2分，整理1分，不等关系1分）‎ ‎ 7分 第22题图②‎ 答：面积至少增加．‎ ‎22．（1）连结，易得，． 2分 点与点的坐标分别是与； 4分 ‎（2）根据题意，． 5分 旋转角度是． 6分 C A E A1‎ B1‎ C1‎ D1‎ B 圆心转过的弧的长为． 8分 ‎23．（1）如图，木柜的表面展开图是两个矩形和．‎ 蚂蚁能够最快到达目的地的可能路径有如图的和．………………………………………………………… 2分 ‎（2）蚂蚁沿着木柜表面经线段到，爬过的路径的长是．……………………………………3分 蚂蚁沿着木柜表面经线段到，爬过的路径的长是． 4分 ‎，最短路径的长是． 5分 ‎（3）作于，则··为所求． 8分 注：作垂线、相似（或等面积）、计算各1分.‎ ‎24．（1）的配方（略）． 3分 ‎（2）． 5分 ‎（3）‎ ‎=． 8分 从而． 9分 即，，．‎ 所以 10分 ‎25．（1）四边形可能的形状有三类：图“矩形”、图“等腰梯形”、图的“四边形”．‎ 注1：画出“矩形”或“等腰梯形”，各给1分；画出另一类图形（后两种可以看作一类），给2分；‎ 等腰梯形不单独画而在后两种图中反映的，不扣分；画图顺序不同但答案正确不扣分．‎ 注2：如果在类似图或图④的图中画出凹四边形，同样给分（两种都画，只给一种的分）．‎ ‎(2) （i）若是直角（图），则四边形为等腰梯形； 6分 ‎（ii）若是锐角（图），存在两个点和，得到等腰梯形和符合条件但不是梯形的四边形； 8分 其中，若是直角（图），则四边形为矩形． 9分 ‎（iii）若是钝角（图④），存在两个点和，得到等腰梯形和符合条件但不是梯形的四边形； 11分 注：可用与或者与是否相等分类；只画矩形和等腰梯形并进行说明可给4分． ‎