人教版中考数学二轮复习专题练习下几何问题-四边形的旋转 27页

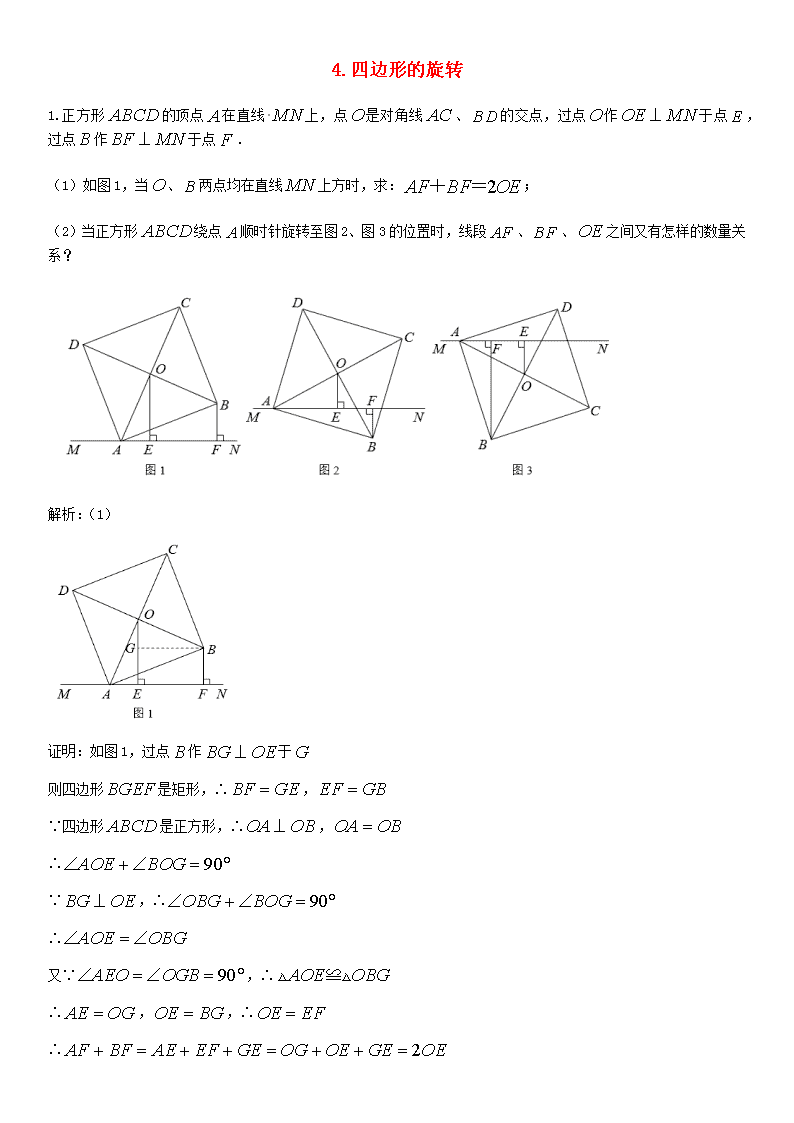
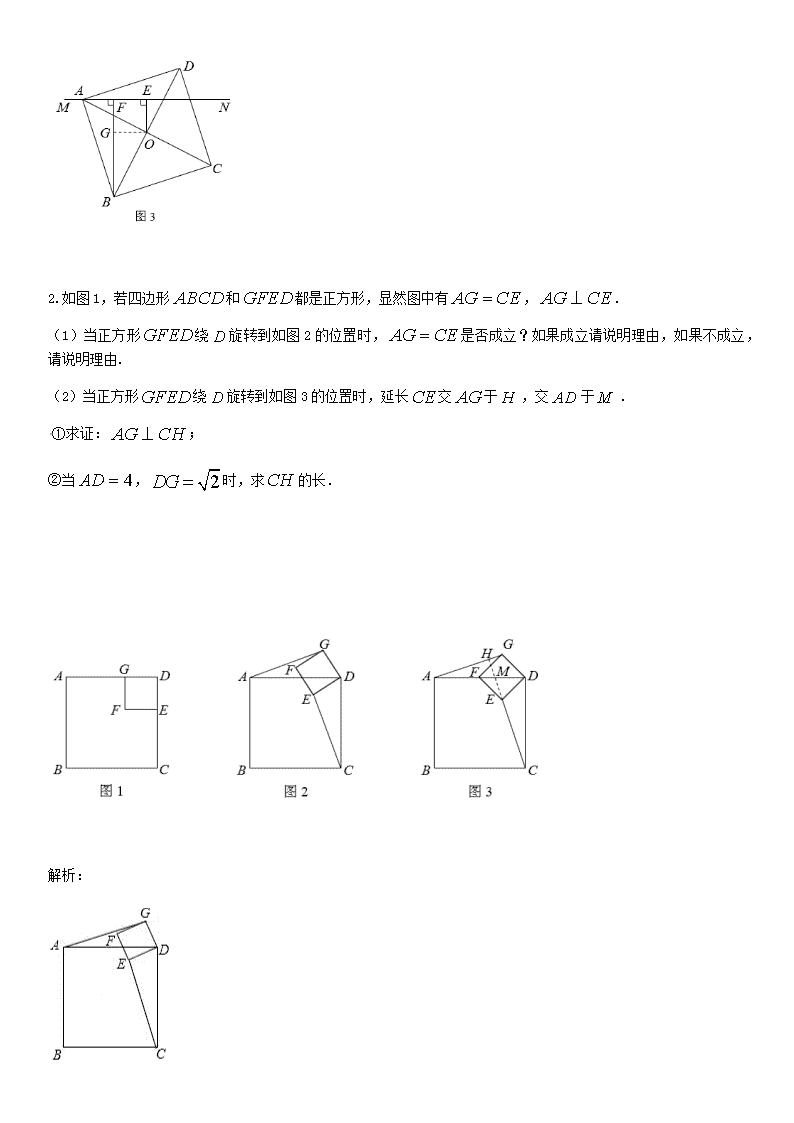
‎4.四边形的旋转 ‎1.正方形的顶点在直线上，点是对角线、的交点，过点作于点，过点作于点．‎ ‎（1）如图1，当、两点均在直线上方时，求：；‎ ‎（2）当正方形绕点顺时针旋转至图2、图3的位置时，线段、、之间又有怎样的数量关系？ ‎ 解析：（1）‎ 证明：如图1，过点作于 则四边形是矩形，∴，‎ ‎∵四边形是正方形，∴，‎ ‎∴‎ ‎∵，∴‎ ‎∴‎ 又∵，∴‎ ‎∴，，∴‎ ‎∴‎ ‎∴‎ ‎（2）‎ 图2结论：‎ 图3结论：‎ 对于图2证明：‎ 过点作交延长线于 则四边形是矩形，∴，‎ ‎∵四边形是正方形，∴，‎ ‎∴‎ ‎∵，∴‎ ‎∴‎ 又∵，∴‎ ‎∴，，∴‎ ‎∴‎ ‎∴‎ 若选图3，其证明方法同上 ‎2.如图1，若四边形和都是正方形，显然图中有，．‎ ‎（1）当正方形绕旋转到如图2的位置时，是否成立？如果成立请说明理由，如果不成立，请说明理由.‎ ‎（2）当正方形绕旋转到如图3的位置时，延长交于，交于．‎ ‎①求证：；‎ ‎②当，时，求的长．‎ 解析：‎ ‎（1）成立．‎ 证明：∵四边形、四边形是正方形，‎ ‎∴，，‎ ‎．‎ ‎∴． ‎ ‎∴．‎ ‎∴． ‎ ‎（2）①类似（1）可得，‎ ‎∴． ‎ 又∵，‎ ‎∴，‎ 即． ‎ ‎ ‎ ‎②连接，交于，连接，‎ ‎∵四边形是正方形，‎ ‎∴，‎ ‎∴，． ‎ ‎∵，，∴，‎ ‎∴以为底边的的高为，（延长画高）‎ ‎∴‎ ‎∴． ‎ ‎3.如图1，正方形与正方形的边、在一条直线上，正方形以点为旋转中心逆时针旋转，设旋转角为，在旋转过程中，两个正方形只有点重合，其它顶点均不重合，连接、．‎ ‎（1）当正方形旋转至图2所示的位置时，求证：；‎ ‎（2）当点在直线上时，连接，求的度数；‎ ‎（3）如图3，如果，，，求点到的距离．‎ 解析：（1）∵正方形与正方形 ‎∴，，‎ ‎∴，∴‎ ‎∴‎ ‎（2）‎ 当点在线段上时，作于 ‎∵，‎ ‎∴，∴，‎ ‎∴‎ ‎∴，∴‎ ‎∴‎ 当点在的延长线上时，作于 ‎∵，‎ ‎∴，∴，‎ ‎∴‎ ‎∴，∴‎ ‎∴‎ ‎（3）‎ 连接、，‎ ‎∵‎ ‎∴点在线段上，∴‎ ‎∴，∴‎ 作于，则 ‎ 在中，‎ ‎∴ ‎ 延长交于 由，得 ‎∴‎ ‎∴ ，∴‎ ‎4.如图1所示，将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起，构成一个大的长方形．现将小长方形绕点顺时针旋转至，旋转角为．‎ ‎（1）当点恰好落在边上时，求旋转角的值；‎ ‎（2）如图2，为中点，且，求证：；‎ ‎（3）小长方形绕点顺时针旋转一周的过程中，与能否全等？若能，直接写出旋转角的值；若不能，说明理由．‎ 解析：‎ ‎（1）∵，∴‎ ‎∴ ‎ ‎∴‎ ‎（2）∵为中点，∴‎ ‎∴‎ ‎∴‎ 又∵，∴‎ ‎∴‎ ‎（3）能．‎ 或.‎ 解：∵四边形为正方形，‎ ‎∴，‎ ‎∵‎ ‎∴与为等腰相等的两等腰三角形.‎ 当与为钝角三角形时，则旋转角.‎ 当与为锐角三角形时，，则旋转角 ‎，即旋转角的值为或时，与全等.‎ ‎5.如图1，△为等腰直角三角形，,是边上的一个动点（点与、不重合），以 为一边在等腰直角三角形外作正方形连接、. ‎ ‎（1）①猜想图1中线段、的数量关系及所在直线的位置关系,直接写出结论；‎ ‎②将图1中的正方形绕着点按顺时针（或逆时针）方向旋转任意角度，得到如图2、图3的情形. 图2中交于点，交于点，请你判断①中得到的结论是否仍然成立. ‎ ‎（2）将原题中的等腰直角三角形改为直角三角形，,正方形改为矩形，如图4，且，，，，交于点，交于点，连接、，求的值.‎ 解析：‎ ‎（1）①‎ 证明：∵ 为等腰直角三角形，，‎ ‎∴‎ ‎∵四边形为正方形.‎ ‎∴，‎ ‎∴‎ ‎∴‎ 延长交于点 ‎∵，‎ ‎∴‎ ‎∴‎ ‎② 仍然成立. ‎ 证明：∵是等腰直角三角形,‎ ‎∴‎ ‎∵四边形是正方形 ‎∴‎ ‎∴‎ 即 ‎∴‎ ‎∴ ‎ 又∵,‎ ‎∴,∴‎ ‎∴‎ ‎（2）证明：‎ 连接 ‎∵四边形是矩形 ‎ ‎∴‎ 又∵ ‎ ‎∴‎ ‎∴‎ 即 ‎∵,,,‎ ‎∴‎ ‎∴‎ ‎∴ ‎ 又∵,‎ ‎∴∴‎ ‎∴‎ ‎∴‎ ‎∴,‎ ‎,‎ ‎∴‎ ‎∵在Rt△中,,,‎ ‎∴‎ ‎∵在中,,,‎ ‎∴‎ ‎∴=‎ ‎6.如图①，在菱形和菱形中，，点、、在同一条直线上，是线段的中点，连结、．‎ ‎（1）求证：，； ‎ ‎（2）将图①中的菱形绕点顺时针旋转，使菱形的对角线恰好与菱形的边在同一条直线上，其他条件不变（如图②），（1）中的结论是否还成立；如果成立，请说明理由，如果不成立请说明理由。‎ ‎（3）若图①中，将菱形绕点顺时针旋转任意角度，其他条件不变（如图③），判断与的位置关系和数量关系．‎ 解析：（1）‎ 证明：如图①，延长交于点 ‎∵，∴‎ 又，，∴‎ ‎∴，‎ ‎∵菱形，菱形，∴，‎ ‎∴，∴，即 ‎ ‎∵，，∴‎ ‎∴‎ ‎（2）‎ 证明：如图②，延长交于点，连结、‎ ‎∵，∴‎ 又，，∴‎ ‎∴，‎ 又，∴‎ 在和中 ‎∵，，‎ ‎∴，∴，‎ ‎∴ ‎ ‎∵，‎ ‎∴，又 ‎∴是等边三角形，∴‎ ‎∴‎ ‎（3）， ‎ 如图③，延长至，使，连结交于点，连结、‎ 则 ‎∴，‎ ‎∴‎ ‎∴‎ 又 ‎∴，又 ‎∴‎ ‎∴，‎ ‎∴ ‎ ‎，∴‎ ‎∴‎ ‎7.如图，四边形和四边形均为正方形，连接与相交于点．‎ ‎（1）试猜想的度数，并说明理由；‎ ‎（2）将正方形绕点逆时针旋转，设的面积为，的面积为，判断与的大小关系；并给予证明；‎ ‎（3）若，，设的面积为，将正方形绕点逆时针旋转一周，求的取值范围．‎ 解析：‎ ‎（1）猜想：，理由如下：‎ ‎∵，∴‎ 又，，∴ ‎ ‎∴‎ 又，∴‎ ‎∴ ‎ ‎（2）‎ 当正方形绕点逆时针旋转时，和总保持相等 证明如下：由于，因此分三种情况：‎ ‎①当时（如图1）‎ 过点作直线于点，‎ 过点作直线于点 ‎∵，∴‎ 又，‎ ‎∴，∴‎ 又，∴‎ ‎∴ ‎ ‎②‎ 当时（如图2）‎ ‎∵，，‎ ‎∴‎ ‎∴ ‎ ‎③‎ 当时（如图3）‎ 和①一样，同理可证 综上所述，在（2）的条件下，总有 ‎ ‎（3）‎ 正方形在绕点旋转的过程中，它的对称中心的轨迹是以点为圆心，为半径的圆（如图4）‎ 因为的边，故当点到的距离取得最大、最小值时，取得最大、最小值 当在直线上时，取得最大值 ‎ ‎ 当在直线上时， 取得最小值 ‎ ‎ 故的取值范围是： ‎ ‎8.如图①，已知是等腰直角三角形，，点是的中点．作正方形，使点，分别在和上，连接，．‎ ‎（1）试猜想线段和的数量关系，请直接写出你得到的结论．‎ ‎（2）将正方形绕点逆时针方向旋转一定角度后（旋转角度大于，小于或等于），如图②，通过观察或测量等方法判断（1）中的结论是否仍然成立？‎ ‎（3）若，在（2）的旋转过程中，当为最大值时，求的值．‎ 解析：‎ ‎（1）． ‎ 证明：∵，‎ ‎，，‎ ‎∴‎ ‎∴.‎ ‎（2）成立．‎ 如图②，连接．‎ ‎∵是等腰直角三角形，，点是的中点．‎ ‎∴，且．‎ ‎∵，．‎ ‎∴，∴．‎ ‎（3）‎ 由（2）知，，故当最大时，也最大．‎ 因为正方形在绕点旋转的过程中，点的轨迹是以点为圆心，为半径的圆，故当正方形旋转到点位于的延长线上（即正方形绕点逆时针方向旋转）时，最大，如图③.‎ 若，则，．‎ 在中，．‎ ‎∴．‎ 即在正方形旋转过程中，当为最大值时，．‎ ‎9.如图1，四边形是正方形，是边上的一个动点（点与、不重合），以为一边在正方形外作正方形，连接，．我们探究下列图中线段、线段的长度关系及所在直线的位置关系．‎ ‎（1）猜想图1中线段、线段的长度关系及所在直线的位置关系；‎ ‎（2）将图1中的正方形绕着点按顺时针（或逆时针）方向旋转任意角度，得到如图2、如图3情形．请你通过观察、测量等方法判断（1）中得到的结论是否仍然成立，并选取图2证明你的判断．‎ 解析：‎ ‎（1），；‎ ‎∵四边形和四边形是正方形，‎ ‎∴，，，‎ ‎∴，‎ 在和中，‎ ‎ ，‎ ‎∴，‎ ‎∴；‎ 延长交于点，‎ ‎∵，‎ ‎∴，‎ 又，‎ ‎∴，‎ ‎∴，‎ ‎∴，即；‎ ‎（2），仍然成立，‎ 在图（2）中证明如下 ‎∵四边形、四边形都是正方形 ‎∴，，‎ ‎∴，‎ ‎∴‎ ‎∴，，‎ 又∵，‎ ‎∴‎ ‎∴‎ ‎∴．‎ ‎10.已知菱形是由绕点顺时针旋转得到的，这两个菱形的边长都是．‎ （1） 如图1，连接，，求证：四边形为矩形；‎ ‎（2）如图2，连接，，，，分别是边，上的两个动点，且满足 ‎．判断的形状，并说明理由； ‎ ‎（3）在（2）的条件下，当时，设的面积为，求的最小值．‎ 解析：‎ ‎（1）证明：‎ 如图1，∵菱形是由菱形绕点顺时针旋转得到的，‎ ‎∴，，，，‎ ‎∴，，．‎ ‎∴四边形是平行四边．‎ ‎∵，，‎ ‎∴，‎ ‎∴，‎ ‎∴．‎ ‎∴平行四边形是矩形；‎ ‎（2）是等边三角形．理由：‎ 证明：如图2∵菱形是由菱形绕点顺时针旋转得到的，‎ ‎∴，，，．‎ ‎∵，‎ ‎∴，‎ ‎∴为等边三角形，‎ ‎∴，‎ ‎∵．，‎ ‎∴，‎ ‎∴．‎ 在和中，‎ ‎，‎ ‎∴，‎ ‎∴，．‎ ‎∵，‎ ‎∴．‎ ‎∵，‎ ‎∴是等边三角形；‎ ‎（3）解：如图2，作于．‎ ‎∵是等边三角形，‎ ‎∴，‎ ‎∴．‎ ‎∴，‎ ‎∴．‎ ‎∴当最小时，最小．‎ ‎∵时，最小．‎ ‎∴．‎ ‎∵，‎ ‎∴．‎ 在中，由勾股定理，得 ‎．‎ ‎∴．‎ 答：的最小值为．‎ ‎11.如图1，四边形、为两个全等的矩形，且矩形的对角线交于点，点在上，．将矩形绕点顺时针旋转角，如图2，、与分别相交于、．‎ ‎（1）则：与的大小关系；‎ ‎（2）若，求旋转角的大小．‎ 解析：‎ ‎（1）‎ 证明：∵四边形是矩形，‎ ‎∴，‎ ‎∵，‎ ‎∴，‎ 将绕点顺时针旋转得到，连接，‎ 则，，，‎ ‎∵，‎ ‎∴，‎ 在和中，‎ ‎，‎ ‎∴，‎ ‎∴，‎ 由三角形的三边关系得，，‎ ‎∴；‎ ‎（2）解：∵，‎ ‎∴是直角三角形，，‎ ‎∵，‎ ‎∴，‎ 在中，，‎ 在中，，‎ ‎∴旋转角为．‎ ‎12.如图，已知正方形．‎ ‎（1）请用直尺和圆规，作出正方形绕点逆时针旋转后得到的正方形（其中，，分别是点，，的像）（要求保留作图痕迹，不必写出作法）； ‎ ‎（2）设与相交于点，求证：；‎ ‎（3）若正方形的边长为，求两个正方形的重叠部分（四边形）的面积．‎ 解析：‎ ‎（1）如图所示：‎ ‎（2）连接．‎ ‎∵正方形由正方形旋转得到，‎ ‎∴，，‎ ‎∴，‎ ‎∴，‎ ‎∴． ‎ ‎（3）‎ 连接．‎ ‎∵正方形，‎ ‎∴．‎ 由题意知，‎ ‎∴，即在上，‎ ‎∴是等腰直角三角形．‎ 设，则．‎ ‎∵，‎ ‎∴，‎ 解得：．‎ 故．‎