北师大版五年级下册数学知识要点归纳 10页

1 第一单元 分数加减法 一、分数的意义 1、分数的意义：把单位“1”平均分成若干份，表示这样的一份或几份的数，叫做分 数。 2、分数单位：把单位“1”平均分成若干份，表示这样的一份的数叫做分数单位。 二、分数与除法的关系，真分数和假分数 1、分数与除法的关系：除法中的被除数相当于分数的分子，除数相等于分母。 2、真分数和假分数： ① 分子比分母小的分数叫做真分数，真分数小于 1。 ② 分子比分母大或分子和分母相等的分数叫做假分数，假分数大于 1或等于 1。 ③ 由整数部分和分数部分组成的分数叫做带分数。 3、假分数与带分数的互化： ① 把假分数化成带分数，用分子除以分母，所得商作整数部分，余数作分子，分母 不变。 ② 把带分数化成假分数，用整数部分乘以分母加上分子作分子，分母不变。 三、分数的基本质 分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变，这叫做分数的 基本性质。 四、分数的大小比较 ① 同分母分数，分子大的分数就大，分子小的分数就小； ② 同分子分数，分母大的分数反而小，分母小的分数反而大。 ③ 异分母分数，先化成同分母分数（分数单位相同），再进行比较。（依据分数的 基本性质进行变化） 五、约分（最简分数） 1、最简分数：分子和分母只有公因数 1的分数叫做最简分数。 2、约分：把一个分数化成和它相等，但分子和分母都比较小的分数，叫做约分。 （并 不是一定要把分数化成与它相等的最简分数才叫约分；但一般要约到最简分数为止） 注意：分数加减法中，计算结果能约分的，一般要约分成最简分数。 六、分数和小数的互化： 1、小数化分数：将小数化成分母是 10、100、1000…的分数，能约分的要约分。具体 是：看有几位小数，就在 1后边写几个 0做分母，把小数点去掉的部分做分子，能约 分的要约分。 2、分数化小数：用分子除以分母，除不尽的按要求保留几位小数。（一般保留三位小 数。） 如果分母只含有 2或 5的质因数，这个分数能化成有限小数。如果含有 2或 5以外的 质因数，这个分数就不能化成有限小数。 3、分数和小数比较大小：一般把分数变成小数后比较更简便。 七、分数的加法和减法 1、分数方程的计算方法与整数方程的计算方法一致，在计算过程中要注意统一分数单 位。 2、分数加减混和运算的运算顺序和整数加减混和运算的运算顺序相同。在计算过程， 整数的运算律对分数同样适用。 3、同分母分数加、减法 ：同分母分数相加、减，分母不变，只把分子相加减，计算 的结果，能约分的要约成最简分数。 4、异分母分数加、减法：异分母分数相加、减，要先通分，再按照同分母分数加减法 的方法进行计算；或者先根据需要进行部分通分。根据算式特点来选择方法。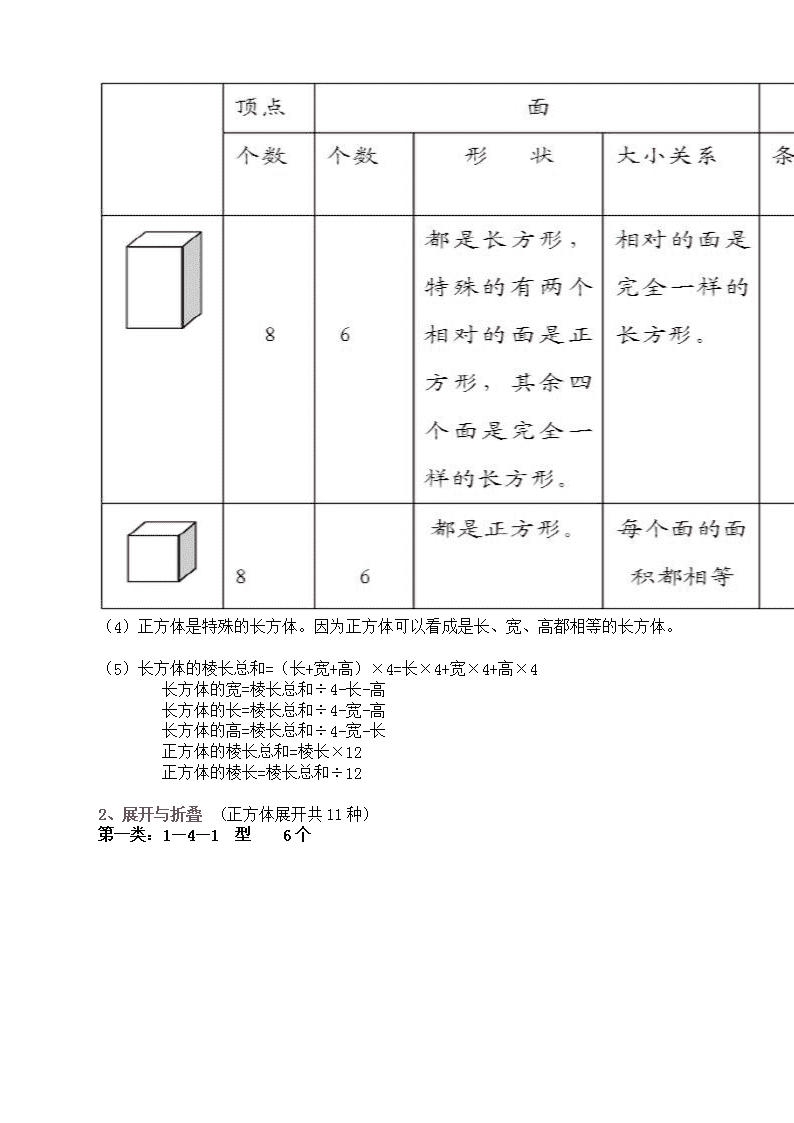 2 第二单元 长方体（一） 1、认识长方体、正方体，了解各部分的名称。 (1) 表面平平的部分称为面；两面相交便形成了一条棱；而三条棱又交于一点，这个 点叫作顶点。 (2) 左面的面叫左面，右面的面叫右面，上面的面叫上面，下面的面叫下面（或叫底 面），前面的面叫前面，后面的面叫后面。 (3) 长方体有 12 条棱，这 12 条棱中有 4条长、4条宽和 4条高。正方体的 12 条棱的 长度都相等。 （4）正方体是特殊的长方体。因为正方体可以看成是长、宽、高都相等的长方体。 （5）长方体的棱长总和=（长+宽+高）×4=长×4+宽×4+高×4 长方体的宽=棱长总和÷4-长-高 长方体的长=棱长总和÷4-宽-高 长方体的高=棱长总和÷4-宽-长 正方体的棱长总和=棱长×12 正方体的棱长=棱长总和÷12 2、展开与折叠 (正方体展开共 11 种) 第一类：1—4—1 型 6 个 第二类：2—3—1 型 3 个 第三类： 2—2—2 型（楼梯形）1 个 第四类：3-3 型 1 个 注意：（1）田字型与凹字型的全错。 （2）正方体展开至少和最多都只剪开 7条棱。 3、长方体的表面积 （1）表面积的意义：是指六个面的面积之和。 （3）长方体的 表面积=长×宽×2 +长×高×2 +宽×高×2 =（长×宽＋长×高＋宽×高）×2 （4）正方体的表面积=棱长×棱长×6 4、露在外面的面 （1）在观察中，通过不同的观察策略进行观察。 如：一种是看每个纸箱露在外面的面，再加到一起； 另一种是分别从正面、上面、侧面进行不同角度的观察，看每个角度都能看到多少个 面，再加到一起。 例如：如图，4个棱长都是 10 厘米的正方体堆放在墙角处，露在外面的面积是多少？ 解：首先应找出有多少个面露在外面： 如果用法一的方法来找：3+1+2+3=9（个）； 如果用法二的方法来找：从上面看有 3个面，从右侧面看有 2个面，从正面看有 4个 面，共有 3+2+4=9（个）。 因为每个面都是面积相等的正方形，所以露在外面的面积=10×10×9=900（厘米 2） 答：露在外面的面积一共是 900 平方厘米。 （2）发现并找出堆放的正方体的个数与露在外面的面的面数的变化规 律。 （3）求露在外面的面的面积=棱长×棱长×露在外面的面的个数。 3 第三单元 分数乘法 分数乘法（一）知识点： (1)理解分数乘整数的意义：分数乘整数意义同整数乘法意义相同，就是求几个相同加 数的和的简便运算。 (2)分数乘整数的计算方法：分母不变，分子和整数相乘的积作分子。能约分的要约成 最简分数。 (3)计算时，应该先约分再计算。 分数乘法（二） 知识点 ： (1) 整数乘分数的意义：求一个数的几分之几是多少。 (2) 理解打折的含义。例如：九折，是指现价是原价的十分之九。 补充知识点： ① 打几折就是指现价是原价的百分之几，例如八五折，是指现价是原价的百分之八十 五。 现价=原价×折扣 原价=现价÷折扣 折扣=现价÷原价 ② 买一赠一打几折： 出一个的钱拿两个货品，即 1除以 2等于零点五，五折 买三赠一打几折： 出三个的钱拿四个货品，即 3除以 4等于零点七五，七五折 分数乘法（三） 知识点： 1、分数乘分数的计算方法：分子相乘做分子，分母相乘做分母，能约分的可以先约分。 （结果是最简分数。） 2、比较分数相乘的积与每一个乘数的大小： ① 真分数相乘积小于任何一个乘数； ② 真分数与假分数相乘积大于真分数小于假分数。 ③ 乘数乘以<1 的数，积<乘数； 乘数乘以=1 的数，积=乘数； 乘数乘以>1 的数，积>乘数； 3、求一个数的几分之几是多少，用乘法。（即已知整体和部分量相对应的分率，求部 分量，用乘法） 4、倒数 （1）如果两个数的乘积是 1，那么我们称其中一个数是另一个数的倒数。倒数是对两 个数来说的，并不是孤立存在的。 （2）当互为倒数的两个数分别作为长方形的长和宽时，长方形的面积是 1。 （3）1的倒数仍是 1；0没有倒数。0没有倒数，是因为 0不能作除数。 （4）求一个数的倒数的方法：把这个数的分子、分母调换位置；其中整数可以看成分 母是 1的分数。 4 第四单元 长方体（二） 一、体积与容积概念 体积：物体所占空间的大小叫作物体的体积。（从外部测量） 容积：容器所能容纳入体的体积叫做物体的容积。（从内部测量） 注意：①同一个容器，体积大于容积；当容器壁很薄时，容积近等于体积。如果容器 壁忽略不计时，容积等于体积。 ②几个物体拼在一起时，它们的体积不发生改变（它们占空间的大小没有发生变化） 二、体积单位 1、认识体积、容积单位 常用的体积单位：立方米（m³）、立方分米（dm³）、立方厘米（cm³） 常用的容积单位：升、毫升，1升=1 立方分米、1毫升=1 立方厘米 2、感受 1 立方米、1 立方分米、1立方厘米以及 1 升、1毫升的实际意义： ① 手指头、苹果、火柴盒体积较小，可用 cm³作单位 ② 西瓜、粉笔盒体积稍大，可以用 dm³作单位 ③ 矿泉水瓶、墨水瓶可以用毫升作单位 ④热水瓶等较大盛液体容器、冰箱可以用升作单位 ⑤我们饮用的自来水用“立方米”作单位 三、长方体的体积 1、长方体、正方体体积的计算方法 ①长方体的体积=长×宽×高，长用 a表示，宽用 b表示，高用 h表示，体积用 V表示， 体积可表示为 V=abh ②正方体的体积=棱长×棱长×棱长，如果棱长用 a表示，体积可表示为 V=a³=a×a×a 长方体（正方体）的体积=底面积×高 V=Sh 补充知识点：长方体的体积=横截面面积×长 2、能利用长方体（正方体）的体积及其他两个条件求出问题。 如：长方体的高=体积÷长÷宽 长=体积÷高÷宽 宽=体积÷高÷长 注意：计算体积时，单位一定要统一； 表面积与体积表示的意义不一样，单位不同，无法比较大小。 四、体积单位的换算 认识体积、容积单位。 常用的体积单位有：立方厘米（cm³）、立方分米（dm³） 、立方米（m³）。 常用的容积单位有：升（L）、毫升（m L） 知识点： 1、体积、容积单位之间的进率：相邻体积、容积单位间进为 1000 1 米³=1000 分米³ 1 分米³=1000 厘米³ 1 升=1 分米³ 1 毫升=1 厘米³ 1 升=1000 毫升 2、体积、容积单位之间的换算方法： 体积、容积单位之间的换算，由高级单位化成低级单位乘进率，由低级单位化成高级 单位除以进率 五、有趣的测量 1、不规则物体体积的测量方法： 一般都是把不规则物体的体积转化成可通过测量计算的水的体积（注意液面是“升高 了”还是“升高到”） 注意：在测量体积较小的不规则物体的体积时，要先测量出一定数量物体的体积，再 算出一个物体的体积 2、不规则物体体积的计算方法：现在液体体积减去原来液体体积 5 第五单元 分数除法 一、分数除法（一） 分数除以整数的意义及计算方法。分数除以整数，就是求这个数的几分之几是多少。 分数除以整数（0除外）等于乘这个数的倒数。 二、分数除法（二） 1、一个数除以分数的意义和基本算理：一个数除以分数的意义与整数除法的意义相同； 一个数除以分数等于乘这个数的倒数。 2、一个数除以分数的计算方法： 除以一个数（0除外）等于乘这个数的倒数。 3、比较商与被除数的大小。 除数小于 1，商大于被除数； 除数等于 1。商等于被除数； 除数大于 1，商小于被除数。 三、分数除法（三） 1、列方程“求一个数的几分之几是多少”的方法： （1）解方程法：设未知数，这里的单位“1”未知，所以设单位“1”为 x，再根据分 数乘法的意义列出等量关系式解这个方程。 （2）算术方法：用部分量除以它所占整体的几分之几 （对应量÷对应分率=标准量） 2、判断单位“1”： ①一般来说，某个数的几分之几，“某个数”就是单位“1” ②数比谁多几分之几或少几分之几，“比”字后面的数量就是单位“1” ③谁是谁的几分之几，“是”字后面的数量就是单位“1” 四、倒数 1、理解倒数的意义： 如果两个数的乘积是 1，那么我们称其中一个数是另一个数的 倒数。倒数是对两个数来说的，并不是孤立存在的。 2、求倒数的方法：把这个数的分子和分母调换位置。 3、1的倒数仍是 1；0没有倒数。（0没有倒数，是因为在分数中，0不能做分母。） 6 第六单元 确定位置 确定位置（一）知识点 1、 认识方向与距离对确定位置的作用。 2、 能根据方向和距离确定物体的位置。 3、 能描述简单的路线图。 确定位置（二）知识点 了解确定物体位置的方法。 能根据平面图确定图中任意两地的相对位臵（以其中一地为观察点，度量另一地所在 方向以及两地的距离） 1、数对：一般由两个数组成。 作用：数对可以表示物体的位置，也可以确定物体的 位置。 2、行和列的意义：竖排叫做列，横排叫做行。 3、数对表示位置的方法：先表示列，再表示行。用括号把代表列和行的数字或字母括 起来，再用逗号隔开。例如：在方格图（平面直角坐标系）中用数对（3，5）表示（第 三列，第五行） （1）在平面直角坐标系中 X轴上的坐标表示列，y轴上的坐标表示行。如：数对（3,2） 表示第三列，第二行。 （2）数对（X，5）的行号不变，表示一条横线，（5，Y）的列号不变，表示一条竖线。 （有一个数不确定，不能确定一个点） 4、两个数对，前一个数相同，说明它们所表示物体位置在同一列上。 如：（2，4）和（2，7）都在第 2列上。 5、两个数对，后一个数相同，说明它们所表示物体位置在同一行上。 如：（3，6）和（1，6）都在第 6行上。 6、图形平移变化规律： （1）图形向左平移，行数不变，列数减去平移的格数。 图形向右平移，行数不变， 列数加上平移的格数。 （2） 图形向上平移，列数不变，行数加上平移的格数。 图形向下平移，列数不变， 行数减去平移的格数。 7 第七单元 用方程解决问题 1、列方程解应用题的步骤： （1）找到题中的等量关系式 （2）解设所求量为 x （3）根据等量关系式列出相应的方程 （4）解答方程，注意计算结果不带单位 （5）检验做答 2、在有多个未知数量的应用题中，通常应将 1倍数设为 x，举例如下： 例：爸爸的年龄是儿子年龄的 4倍，父子俩年龄之和为 40，求父亲和儿子的年龄各是 多少岁？ 解：首先根据题意找出等量关系式：爸爸年龄+儿子年龄=40 因为儿子年龄是 1倍数，所以：设儿子年龄为 x岁，那么爸爸年龄就是 4x，代入等量 关系式得： 爸爸年龄为：4x=4×8=32(岁) 答：爸爸的年龄为 32 岁，儿子的年龄为 8岁。 3、相遇问题涉及到的公式： 路程=速度×时间 时间=路程÷速度 相距距离=速度和×相遇时间 8 第八单元 数据的表示和分析 1、条形统计图 优点：很容易看出各种数量的多少。 注意：画条形统计图时，直条的宽窄必须相同。 取一个单位长度表示数量的多少要根据具体情况而确定； 复式条形统计图中表示不同项目的直条，要用不同的线条或颜色区别开，并在制图日 期下面注明图例。 2、折线统计图 用一个单位长度表示一定的数量，根据数量的多少描出各点，然后把各点用线段顺次 连接起来。 优点：不但可以表示数量的多少，而且能够清楚地表示出数量增减变化的情况。 注意：折线统计图的横轴表示不同的年份、月份等时间时，不同时间之间的距离要根 据年份或月份的间隔来确定。 3、扇形统计图 用整个圆的面积表示总数，用扇形面积表示各部分所占总数的百分数。 优点：很清楚地表示出各部分同总数之间的关系。