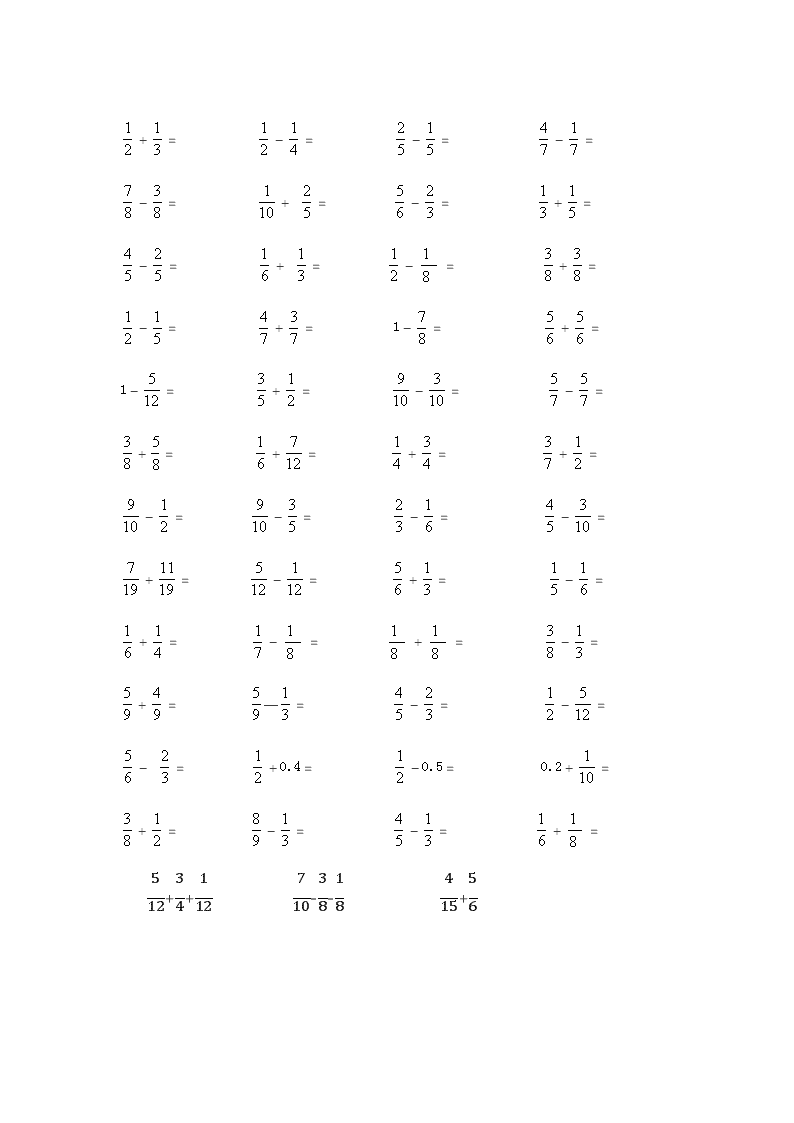人教版小学数学五年级下册专项练习（16份） 59页

2 1 ＋ 3 1 ＝ 2 1 － 4 1 ＝ 5 2 － 5 1 ＝ 7 4 － 7 1 ＝ 8 7 － 8 3 ＝ 10 1 ＋ 5 2 ＝ 6 5 － 3 2 ＝ 3 1 ＋ 5 1 ＝ 5 4 － 5 2 ＝ 6 1 ＋ 3 1 ＝ 2 1 － 8 1 ＝ 8 3 ＋ 8 3 ＝ 2 1 － 5 1 ＝ 7 4 ＋ 7 3 ＝ 1－ 8 7 ＝ 6 5 ＋ 6 5 ＝ 1－ 12 5 ＝ 5 3 ＋ 2 1 ＝ 10 9 － 10 3 ＝ 7 5 － 7 5 ＝ 8 3 ＋ 8 5 ＝ 6 1 ＋ 12 7 ＝ 4 1 ＋ 4 3 ＝ 7 3 ＋ 2 1 ＝ 10 9 － 2 1 ＝ 10 9 － 5 3 ＝ 3 2 － 6 1 ＝ 5 4 － 10 3 ＝ 19 7 ＋ 19 11 ＝ 12 5 － 12 1 ＝ 6 5 ＋ 3 1 ＝ 5 1 － 6 1 ＝ 6 1 ＋ 4 1 ＝ 7 1 － 8 1 ＝ 8 1 ＋ 8 1 ＝ 8 3 － 3 1 ＝ 9 5 ＋ 9 4 ＝ 9 5 — 3 1 ＝ 5 4 － 3 2 ＝ 2 1 － 12 5 ＝ 6 5 － 3 2 ＝ 2 1 ＋0.4＝ 2 1 －0.5＝ 0.2＋ 10 1 ＝ 8 3 ＋ 2 1 ＝ 9 8 － 3 1 ＝ 5 4 － 3 1 ＝ 6 1 ＋ 8 1 ＝ 5 12 +3 4 + 1 12 7 10 -3 8 -1 8 4 15 +5 6 1 2 -（3 4 -3 8 ） 5 6 -（1 3 + 3 10 ） 2 3 +5 6 五年级下学期应用能力测试 1、 张大伯收了一批西瓜，第一天卖出了总数的 5 1 ，第二天卖出了总数的 6 1 ，两天共卖出 总数的几分之几？ 2、有一个平行四边形的面积是 36 平方分米，它的高是 12 分米，底是多少分米？（用方程 解） 3、王彬看一本书，第一天看了全书的 9 2 ，第二天比第一天多看了全书的 27 4 。两天一共看 了全书的几分之几？ 4、张大伯收了 1 2 吨西瓜，第一天卖出总数的 1 5 ，第二天卖出总数的 1 10 。还剩总数的 几分之几？ 5、李庄有耕地 90 公顷，其中 24 公顷是旱地，66 公顷是水地。 (1)旱地的面积占耕地总面积的几分之几? (2)旱地的面积相当于水地面积的几分之几? 6、一盒糖果，5 个 5 个地数，或者 6 个 6 个地数都正好数完。请问这盒糖果最少有多少个？ 7、把两根分别长 24 分米和 30 分米的木料锯成若干相等的小段而没有剩余，每段最长是多 少分米？ 8、大厅里挂着一只钟，它的时针长 12 厘米，这根时针的尖端一昼夜走了多少厘米？ 9、有一位老人说：“把我的年龄加上 17，再用 4 除，再减去 15 后乘以 10，恰好是 100 岁。”这位老人有多少岁？ 10、小明和小芳原来共有 80 枚邮票，小明给了小芳 8 枚后，两人的邮票数相同，原来两人 各有多少枚邮票？ 11、东方广场有一个圆形喷泉，周长是 37.68 米，面积是多少平方米？ 12、一辆自行车的车轮半径是 36 厘米。这辆自行车通过一条 720 米长的街道时，车轮要转 多少周？ 13、公园里有一个直径是 8 米的圆形花坛，花坛的周围有一条 1 米宽的小路。这条小路的面 积是多少平方米？ 14、将自然数排列如下， 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 一共可以盖住多少个不同的和？ 奥数辅导班专用 五年级数学思维训练春季期中测 试卷 【总分 100 分 时间 120 分】 一、基础知识部分 一、认真看，仔细填。（15 分，每空 1 分） 1、用 5 个完全一样的正方体拼成一个长方体，表面积减少 24 平方厘米，这个长 方体的表面积是______________平方厘米。 2、 同时是 2、3、5 的倍数的最小两位数是________，最大两位数是________， 最小三位数是________。 3、两个质数的和是 10，积是 21，它们分别是_________和_________。 4、千位上是最大的一位数，百位上是最小的合数，十位上是最小的质数，个位 上是最小的自然数，这个数是____________。 5、一根长方体木料的体积是 4.5 立方分米，横截面的面积是 0.5 立方分米，木 料的长有____________分米。 6、有一个长方体木块长 6 厘米，宽 4 厘米，高 3 厘米，如果把它切成 1 立方厘 米的小方块，可以切 出____________块。 7、2 7 的分母增加 14，要使分数的大小不变，分子要________________________。 8、既是 2 和 5 的倍数，又是 3 的倍数的最小三位数是多少____________。 9、把 2 米平均分成 9 份，每份长____________米，每份是总长的____________。 10、一个正方体的棱长和是 36cm，它的体积是_______________，表面积是 ______________。 二、选择题。（12 分，每题 2 分） 1、若连续的四个自然数都为合数，那么，这四个数之和的最小值为（ ）。 A、101 B、100 C、102 D、110 2、一个正方体的棱长扩大 3 倍，它的体积扩大（ ）倍。 A、3 B、9 C、27 3、已知 4 个质数的积是它们和的 11 倍，则它们的和为（ ）。 A、48 B、47 C、46 D、没有符合条件的数 4、要使三位数“56□”能被 3 整除，“□”里最大能填（ ）。 A、7 B、8 C、9 5、一根长方体木料，它的横截面积是 9cm2，把它截成 2 段，表面积增加（ ） cm2 A、9 B、18 C、27 6、下面的平面图中，（ ）号不能折成正方体。 A、 B、 C、 三、判断。对的在括号里打“√”，错的打“×”。（5 分，每空 1 分） 1、2 个棱长 1cm 的正方体拼成一个长方体，长方体的表面积是 12cm2。 （ ） 2. 长方形的两条对称轴相交于点 O，绕点 O 旋转长方形 180°后与原来图形重合。 （ ） 3. a³=a+a+a。 （ ） 4. 两个质数的和一定是偶数。 （ ） 5. 妈妈给了我一个苹果，我一口气吃了4 3 个。 （ ） 四、计算题。（共 17 分） 1、直接写出得数。（9 分） 1.53－0.5＝ 7.8＋0.9＝ 7.5－2.5＝ 12÷0.4＝ 0.56＋4.44＝ 2.9＋3.7＋2.1＝ 4×0.25＝ 1.25×5×8＝ 7.6×8＋2.4×8＝ 2、计算下面立体图形的表面积和体积。（单位：cm）（8 分） 二、数学思维训练部分 五、解决问题。（51 分） 1、一个长方体和一个正方体的棱长总和相等，已知正方体的棱长 6cm，长方体 的长 7cm，宽 6cm，那么长方体的高是多少 cm？它们的体积相等吗？（6 分） 2、一个棱长是 5 分米的正方体鱼缸，里面装满水，把水倒入一个底面积 50 平方 分米的长方体鱼缸里，长方体鱼缸里的水有多深？（6 分） 3、一本书的中间被撕掉了一张，余下的各页码数的和恰好是 1000，问：这本书 有多少页？撕掉的是那一页？（6 分） 8 4 5 7 7 7 4、一个长方体木块，从下部和上部分别截去高为 3 厘米和 2 厘米的长方体后， 便成为一个正方体，表面积减少了 120 平方厘米，原来长方体的体积是多少立方 厘米？（6 分） 5、我们的祖先早在公元前 700 多年就发明了用水漏计时的方法，科技小组的同 学也尝试做了一个长方体水漏计时器，这个计时器长 4dm，宽 2dm，高 3dm，全 部漏完要 8 小时．某天中午 12 时，同学们往水漏计时器里加满了水，下午 5 时 放学时，水漏计时器里大约还有多少升水？（6 分） 6、用大、小两种汽车运货，每辆大汽车装 18 箱，每辆小汽车装 12 箱，现在有 18 车货，价值 3024 元，若每箱便宜 2 元，则这批货价值 2520 元，问：大、小 汽车各有多少辆？（6 分） 7、一个长方体，如果它的长增加 2 厘米，体积就增加 20 立方厘米；如果宽增加 3 厘米，体积就增加 60 立方厘米；如果高增加 5 厘米，体积就增加 40 立方厘米。 请回答：原来这个长方体的表面积是平方厘米？（7 分） 8、把 11 块相同的长方体砖拼成了一个大长方体，已知大长方体的棱长总和是 188 厘米，求每一块砖的体积。（8 分） 五年级下册数学竞赛试卷 班级 姓名 一、 填空题（每空 2 分，合计 34 分） 1、一个正方体棱长 5 分米，两个这样的正方体拼成一个长方体，这 个长方体的棱长之和是( )分米，表面积是 ( )平方分米，体积是( )立 方分米。 2、一个长方体棱长之和是 84cm，它的长是 8cm，宽是 7cm，高是 ( )cm，它的表面积是( )平方厘米， 体积是( )立方厘米 3、三个连续奇数的和是 21，这三个奇数分别是( )、 ( )、( )。 4、把一条 3 分米长的线对折后再对折两次，折后每段长是全长的 （ ），每段长是（ ）分米。 5、一个分数，分子和分母的和是 28。如果分子减去 2，这个分数就 等于 1，原分数是（ ）。 6、一个电话号码是 7 位数，逆时针旋转 90°，再旋转 90°，是 9160619。 原 电话号码是（ ）。 7、一间长方体形状的教室长 8 米，宽 6 米，高 4 米，里面坐着 50 名 学生，平均每人占地（ ）平方米，平均每人占有 空间（ ）立方米。 8、一个长 3 分米的长方体木料被截成两个长方体后，表面积增加了 18 平方分 米，原来长方体木料的体积是（ ）立方分 米。 9、妈妈买回一筐鸡蛋（没有 100 个），2 个 2 个地数，最后多 1 个； 3 个 3 个地数，最后也多 1 个；4 个 4 个地数，最后也多 1 个；5 个 5 个地数，最后也多 1 个；6 个 6 个地数，最后还是多 1 个。算一算： 妈妈买了( )个鸡蛋。 二、 判断题（每题 2 分，合计 10 分） 1．被除数÷ （除数×商）= 1 。 （ ） 2．如果 a 与 b 的最大公因数是 1 ，那么a b 一定是最简分数。a≠b （ ） 3． 左图梯形中两个阴影的三角形面积一定相等。 （ ） 4．张老师今年 2 月 26 日出发，5 天后返回，回来时是 3 月 4 日。 （ ） 5．一个长方体，它的长、宽、高都扩大 2 倍，它的体积扩大 6 倍。 ( ) 三、计算下面各题（能简算的要简算）（每题 4 分，合计 16 分） 1.25×3.2×2.5 1 2 + 3 4 - 3 10 14 15 - （ 5 3 - 7 10 ） 8 - 9 16 - 7 16 四、 解决问题（每题 8 分，合计 32 分）【在草稿本上算出得数，直 接填答。】 1、 有一个长方体，它的长、宽、高是三个连续的自然数，且体积 是 210 立方米，长方体的长、宽、高各是多少？ 答：长方体的长是（ ）米，宽是（ ）米，高是（ ） 米。 2、有一块长 14 厘米，宽 9.8 厘米，高 3 厘米的铁块，浸没在一个长 方形的油 箱中。取出铁块后，油的高度下降了 1.2 厘米。这个长方体油箱的底 面积是多少平方厘米？ 答：这个长方体油箱的底面积是（ ） 平方厘米。 3、某厂三月上旬前 4 天共节约用水 140 吨，后 6 天平均每天节约 32.5 吨。这个厂三月上旬平均每天节约用水多少吨？ 答 ： 这 个 厂 三 月 上 旬 平 均 每 天 节 约 用 水 （ ）吨。 4、有甲乙两个车间，甲车间有 132 人，乙车间有 144 人。因工作需 要从甲车间调若干人到乙车间后，乙车间人数正好是甲车间的 2 倍。 甲车间需调多少人到乙车间？ 答：甲车间需调（ ）人 到乙车间。 五、求面积。（单位：厘米）（每题 4 分，合计 8 分） 【在草稿本上算出得数，直接填空。】 (1)边长为 4cm 相等的四个正方形中，画了两个三角形，求这两个三 角形的面积之和。 这两个三角形的面积之和是 （ ） 平方厘米。 (2) 求下图阴影部分 阴影部分的面积是（ ） 平方厘米。 人教版第二学期五年级数学计算能力竞赛 (答 卷 时 间：10 分 钟 完 成，总分：100 分) 姓名： 成绩： 一、口算。（40 分） 0.24＋6.9 = 9.1－7.3 = 1.2×6 = 7.2＋2.8= 31×3 = 24×5 = 1000÷8 = 0.8×0.6 = 1.25×4 = 300÷50 = 480÷0.6 = 0.15×9= 3.4×0.7= 2.2×3 = 0.2×1.1 = 2.1÷0.3=  5 1 5 2  8 3 8 5  9 4 9 5  4 11 二、下面各题,各样简便就怎样算。（60 分） 2.15+8.73+1.27+7.85 11.87-(8.2+1.87) 5.42-3.87-1.13 4.38－1.56+0.62－0.44 0.4×270×2.5 （40+1.25）×8 48 平方厘米 （12.5－0.05）×8 2.6×8.5+8.5×7.4 9.9×6.9－6.9×3.9 5.6×99+5.6 2.5×(1.9＋1.9＋1.9＋1.9) 7.2÷1.25÷8 五年级计算题练习一 班级 姓名 得分 一、直接写出得数。（4 分） 10 1 － 20 1 = 2＋ 2 1 = 4 1 ＋ 4 3 － 5 1 = 9 7 － 9 2 = 1－ 2 1 － 5 1 = 5 1 ＋ 2 1 － 5 1 = 3 1 ＋ 3 5 －2= 5 2 ＋ 10 1 = 二、解方程或比例。（9 分） ① 0.3χ= 45 ② 5 2 χ＋ 5 3 χ=28 ③χ－ 5 4 = 12 5 三、计算，要写出主要计算过程，能用简便方法的要用简便方法计算。（18 分） 5 1 ＋ 2 1 ＋ 3 1 2 1 ＋ 3 1 － 4 1 5 1 ＋ 2 1 ＋ 5 4 2－12 5 －12 7 7 9 ＋ 6 1 ＋ 6 5 ＋ 7 5 15 13 －（15 13 － 5 2 ） 五年级计算题练习二 班级 姓名 得分 一．直接写出得数。（4 分） 2 1 ＋ 2 1 = 3 1 ＋ 3 2 = 1－ 6 5 = 6 5 － 6 5 = 5 1 ＋ 5 1 = 5 4 － 5 1 = 8 3 ＋ 8 3 = 1－ 2 1 = 二．解方程或比例。（9 分） Ⅹ－ 2 1 = 5 4 6 1 ＋Ⅹ= 2 1 2Ⅹ－ 6 5 = 6 1 三．计算下列各题，要写出主要计算过程，能用简便方法的要用简便方法计算。（18 分） （1） 5 4 ＋（ 8 3 － 4 1 ） （2）2－ 7 3 － 7 4 (3) 8 5 － 3 1 ＋12 5 （4）68－ 7.5 ＋ 32－2.5 （5）12 5 －（12 1 － 2 1 ） 五年级计算题练习三 班级 姓名 得分 一．直接写出得数。（4 分） 9 2 ＋ 2 1 = 7 6 － 3 2 = 10 3 ＋ 4 1 = 7 3 ＋ 9 1 = 3 1 － 5 1 = 6 1 ＋ 4 1 = 7 5 － 5 1 = 20 17 － 20 3 － 20 9 = 9 2 ＋ 8 3 － 8 5 = 7－ 7 5 = 14 1 ＋ 14 5 ＋ 14 3 = 4 1 ＋ 4 1 ＋ 4 3 = 1－ 3 2 － 3 1 = 二．解方程或比例。（9 分） X＋1 3 =6 7 7 12 —x = 1 4 X－( 7 16 － 5 24 )= 7 24 三．计算下列各题，要写出主要计算过程，能用简便方法的要用简便方法计算。（18 分） 5 1 ＋ 3 1 ＋ 5 4 1－11 5 －11 6 7 2 ＋ 6 1 ＋ 6 5 ＋ 7 5 15 13 －（15 13 － 5 2 ） 8 9 －（2 9 ＋1 3 ） 11 15 ＋10 17 ＋ 4 15 ＋ 5 17 五年级计算题练习四 班级 姓名 得分 一．直接写出得数。（4 分） 0.15×0.6= 7÷40= 2－1 3 = 2 5 ＋4 5 = 1 2 ＋2 3 = 1.2÷2.4= 1 3 －1 4 = 0.64÷8= 0.75÷0.25= 10－0.06= 5 12 ＋ 7 12 = 12.5×80= 5 8 ＋7 8 = 0.53= 1 3 ＋1 6 = 5— 1 6 = 二．解方程或比例。（9 分） ①χ+ 3 7 = 3 4 ②χ- 5 12 = 3 8 ③χ-5 6 =1 三．计算下列各题，要写出主要计算过程，能用简便方法的要用简便方法计算。（18 分） ① 17 20 －（ 7 20 ＋ 5 12 ） ② 8 9 －（2 9 ＋1 3 ） ③ 2 9 + 4 5 + 7 9 + 1 5 ④ 7- 5 7 - 5 7 ⑤ 4 5 + 11 15 + 3 10 ⑥ 6- （3 4 - 2 5 ） 五年级计算题练习五 班级 姓名 得分 一、直接写出得数。（4 分） 8 7 + 2 1 ＝ 2 1 + 3 1 ＝ 8 1 － 9 1 ＝ 4 3 － 2 1 ＝ 1+ 13 6 ＝ 5 3 + 5 2 ＝ 3 2 － 6 1 ＝ 8 1 + 3 1 ＝ 10 3 + 3 2 ＝ 8 7 － 4 3 ＝ 5 2 + 10 3 ＝ 1－ 15 11 ＝ 7 4 － 2 1 ＝ 4 1 + 4 1 ＝ 7 2 + 14 1 ＝ 6 2 ＝ 5 3 ＝ 0.125×8＝ 6.25×13＝ 28÷56＝ 二、解方程或比例。（9 分） 3 7 χ＋ 1 8 = 1 2 4χ－1.6χ＝36 X＋ 7 3 = 4 3 三、递等式计算，怎样简便就怎样算。（18 分） 7.8－8.75＋2.2－1.25 7.8×1.17－7.8×0.17 ③ 7－ 7 3 － 7 4 ④ 17 13 －（ 17 5 ＋ 10 1 ） ⑤ 5 1＋（ 6 5 － 18 13 ） 五年级计算题练习六 班级 姓名 得分 一．直接写出得数。（4 分） 5 6 ＋4 9 ＝ 7 10 －1 5 ＝ 3 5 －1 4 ＝ 5- 4 1 = 1-1 5 - 5 4 = 5÷0.001= 2.5×4= 3 1 + 4 1 = 5 1 - 6 1 = 15 11 + 11 4 + 15 4 = 二. 解方程或比例。（9 分） X＋3 5 = 7 10 2X－ 5 1 =1- 5 1 5.5X-3X＝ 15 三．脱式计算，写出主要计算过程，能用简便算法的要用简便算法。（18 分） 5 3 －（ 15 2 ＋ 3 1 ） 6 5 － 4 1 － 3 1 12 5 ＋ 5 3 ＋ 12 7 ＋ 5 2 7 3 ＋ 4 3 － 14 11 9 5 ＋ 12 7 ＋ 9 4 11 15 － 8 3 － 8 5 五年级计算题练习七 班级 姓名 得分 一．直接写出得数。（4 分） 2 1 ＋ 2 1 = 3 1 ＋ 2 1 = 1－ 6 5 = 6 5 － 6 5 = 5 1 ＋ 5 1 = 10 4 － 5 1 = 8 3 ＋ 8 3 = 2－ 2 1 = 二. 解方程或比例。（9 分） ① Ⅹ－ 7 5 = 5 4 ② 2Ⅹ－ 6 5 = 6 1 ③ 11 4 11 2 11 3 X 三．脱式计算，写出主要计算过程，能用简便算法的要用简便算法。（18 分） 11 6 13 5 11 5  )8 3 6 5(6 1  )5 4 12 7(12 7  14 6 2 1 14 1  9 6 7 5 9 3 7 2  15 8 15 72  五年级计算题练习八 班级 姓名 得分 一．直接写出得数。（4 分） 1 2 ＋2 3 = 1.2÷2.4= 1 3 －1 4 = 0.64÷8= 0.75÷0.25= 10－0.06= 5 12 ＋ 7 12 = 12.5×80= 2.4 0.03= 0.5＋1 3 ＝ 7.5－2.5＝ 0.39÷13= 5 8 ＋7 8 = 0.53= 1 3 ＋1 6 = 5— 1 6 = 二. 解方程或比例。（9 分） x＋ 8 3 = 6 5 x－ 6 1 = 12 3 x－( 14 3 ＋ 7 4 )= 2 1 三．脱式计算，写出主要计算过程，能用简便算法的要用简便算法。（18 分） 5 4 + 15 11 + 10 3 60.62－（9.2＋12.62） 6.8＋ 6 1 ＋3.2＋ 6 5 11 15 － 7 3 － 7 4 11 9 ＋ 6 5 ＋ 11 2 － 6 1 8 7 －（ 10 7 － 8 1 ） 五年级计算题练习九 班级 姓名 得分 一．直接写出得数。 9 2 ＋ 9 5 = 7 2 ＋ 7 5 = 8 5 ＋ 8 1 = 6 5 － 6 1 = 10 7 －10 1 = 9 7 － 9 2 = 5 1 ＋ 5 3 = 12 11 －12 9 = 1－ 5 3 = 7 4 － 7 1 = 8 7 － 8 3 = 5 4 ＋ 5 3 = 5 3 － 5 3 = 8 5 ＋ 3 1 = 2 1 ＋ 5 1 = 二. 解方程。 X＋1 3 =6 7 7 12 —x = 1 4 X－( 7 16 － 5 24 )= 7 24 三．脱式计算，写出主要计算过程，能用简便算法的要用简便算法。 9 5 ＋（ 4 3 ＋ 2 1 ） 10 1 ＋ 8 3 － 5 2 5 3 －（15 2 ＋ 3 1 ） 6－（ 4 3 － 5 2 ） 4 1 ＋ 3 1 ＋ 4 1 ＋ 3 2 7 9 ＋ 8 1 ＋ 8 3 ＋ 7 5 5－ 9 4 － 9 5 15 8 －（15 8 ＋18 7 ） 五年级计算题练习十 班级 姓名 得分 一．直接写出得数。 2 5 + 3 5 = 6.8–0.08＝ 5 6 —5 6 ＝ 160×5＝ 1.44÷9＝ 4 5 + 3 5 ＝ 2.76×100＝ 8.7–1.9–3.1＝ 5 6 + 1 ＝ 1 5 - 1 7 ＝ 0.14×6＝ 48÷0.6 ＝ 0.15×0.6= 7÷40= 2－1 3 = 2 5 ＋4 5 = 二. 解方程。ww w.xkb 1. com Ⅹ－ 7 5 = 5 4 6 1 ＋Ⅹ= 8 7 Ⅹ－ 5 3 = 10 7 三．脱式计算，写出主要计算过程，能用简便算法的要用简便算法。 5 1 ＋ 2 1 ＋ 3 1 2 1 ＋ 3 1 － 4 1 2－（ 3 1 ＋ 3 5 ） 2 1 ＋10 3 － 5 1 7 9 ＋ 6 1 ＋ 6 5 ＋ 7 5 15 13 －（15 13 － 5 2 ） 长方体和正方体切拼练习题 一、判断： （1）长方体有 6 个面，可能会有 4 个面面积相同。（ ） （2）棱长是 6 分米的正方体体积与表面积一样大。（ ） （3）1 立方米铁的体积比 1 立方米的棉花体积大。 （ ） （4）体积为 1 立方分米的纸盒放在桌面上，纸盒所占的面积一定是 1 平方分米。 （ ） （5）正方体的棱长扩大 2 倍，体积扩大 4 倍。（ ） 二、应用题： 一个长方体，长 12 厘米，宽 8 厘米，高 6 厘米。 （1）如果从这个长方体上切下一个最大的正方体，这个正方体的体积应该是多 少？ （2）如果将这个长方体切成若干个大小一样的正方体（不许有剩余），最少能 切多少块？ （3）如果用若干个这样相同的长方体拼成一个更大的正方体，至少需要多少个 长方体？ 三、练习 1.把一个长 16 厘米，宽 6 厘米，高 8 厘米的大长方体切成两个小长方体，这两 个小长方体的表面积的和最大是多少平方厘米，最小是多少？ 2.一个正方体的表面积是 24 平方分米，把它分成两个完全相同的长方体，每个 长方体的表面积是多少平方分米？ 3.把一个长 6 厘米，宽 5 厘米，高 4 厘米的长方体木块锯成两个小长方体，表面 积最少增加多少平方厘米?最多增加多少平方厘米? 4.把 1 立方米的正方体木料，全锯成 1 立方厘米的小木块（损耗不在计算之内）， 把这些小木块一个紧挨一个地排成一行，这一行总共有多少米 5.一个正方体木块，表面积是 30 平方分米，如果把它据成大小一样的 8 个小正 方体木块，每个小木块的表面积是多少？ 6.把长 5 厘米、宽 4 厘米、高 3 厘米的两块相同的长方体拼成一个新长方体，有 几种拼法，表面积分别是多少？ 7.把两块棱长 5 厘米的正方体的拼成一个长方体，这个长方体的表面积是多少平 方厘米？（你能用几种方法解答） 8.一个正方体的底面周长是 16 厘米，它的表面积是多少平方厘米，体积是多少 立方厘米？ 9.至少要几个小正方体才能拼成一个大正方体，如果一个小正方体的棱长是 5 厘米，那么大正方体的表面积是多少平方厘米，体积是多少立方厘米？ 10.一个长方体，如果高减少 3 厘米，就成为一个正方体。这时表面积比原来减 少了 96 平方厘米。原来长方体的体积是多少立方厘米？ 11.一个长 2 米的长方体钢材截成三段，表面积比原来增加 2.4 平方分米，这根 钢材原来的体积是多少立方分米？ 12.一个长方体，如果长减少 2 厘米，就成为一个正方体，这时，正方体的表面 积是 96 平方厘米，原来长方体的体积是多少？ 13.将三个棱长是 4 厘米的正方体拼成一个长方体，这个长方体的体积是多少立 方厘米，表面积是多少平方厘米？ 14.一个长方体，如果高减少 3 厘米，就成为一个正方体。这时表面积比原来减 少了 96 平方厘米。原来长方体的体积是多少立方厘米？ 15.一个棱长是 3 厘米的正方体木块，各面中心凿穿一孔面边长是 1 厘米的正方 形柱孔，它余下的体积是多少立方厘米？ 时间：20 分钟 1、把一根7 8 米长的钢管锯成三段，第一段长1 4 米，比第二段短1 8 米，第三段长 多少米？ 2、打字员打一份 5 万字的稿件，第一天打了全稿的1 3 ，第二天比第一天多打全 稿的1 4 ，还剩几分之几没有打？ 3、某化肥厂生产一批化肥，结果上半月完成了计划的4 5 ，下半月完成了计划的 7 15 ，上半月比下半月多完成几分之几？ 4、一堆煤，上月用了1 2 吨，这个月用了1 3 吨，还剩3 5 吨，这堆煤共有多少吨？ 5、修路队修一条 50 千米长的路，第一天修了全长的1 6 ，第二天修了全长的1 2 ， 第三天修了全长的1 5 ，还剩几分之几没有修？ 6、某筑路队修筑一条公路，第一天修了3 4 千米，比第二天少修1 2 千米，还剩14 3 千米没有修。这段公路有多长？ 7、一根铁丝，第一次用去 12 5 米，第二次用去 8 7 米。（1）两次共用去多少米？ （2）第二次比第一次多用去多少米？ 8、小明看一本故事书，已经看了全书的 9 4 ，还剩下几分之几没有看？已经 看的比剩下的少几分之几？ 9、修一条路，第一天修了全长的 5 2 ，第二天修了全长的 7 2 ，第三天要把剩 下的全修完。第三天修了全长的几分之几？ 10、一个果园要种桃树、苹果树和梨树，其中种的桃树和梨树占总面积的 16 13 ， 苹果树和梨树占总面积的 8 5 。梨树的面积占总面积的几分之几？ 11、小李身高 5 8 米，小张比小李高 20 1 米，小王又比小张高 50 1 米，小王和 小张的身高各是多少米？ 12、一批苹果，第一天卖出了总数的2 5 ，第二天卖出总数的1 4 ，两天一共卖出总 数的几分之几？ 13、一个长方形长是7 5 米，宽是1 3 米。它的周长是多少米？ 14、一根铁丝，第一次用去它的1 4 ，第二次用去它的1 3 ，还剩下全长的几分之几？ 15、服装厂本月计划生产一批童装，结果上半月完成了2 3 ，下半月和上半月完成 的同样多，超产了吗？如果超产，超产了几分之几？ 16、 一个三角形三条边的长度分别是1 5 米， 3 10 米和1 2 米，这个三角 形的周长是多少米？ 填空题专项复习题 1、 在括号里填上合适的计量单位。 （1）一个药水瓶的容积是 100（ ）。 （2）一间教室的占地面积是 50（ ）。 （3）一间教室的容积是 170（ ）。 （4）一个玻璃鱼缸的容积是 60（ ）。 2、 5.02 3m = （ ）d 3m 4.08L = ( )ml 3、 12.43 d 3m =( ) d 3m ( )c 3m 800ml=( )c 3m =( ) d 3m 4、一个长方体的长是 3dm,宽 2 dm，高是 1.5 dm，它的表面积是（ ），体积是 （ ）。 5、一个正方体的棱长总和是 24 dm，它的棱长是（ ），表面积是（ ），体 积是（ ）。 6、一个可乐瓶上标着 1.25 L，说明可乐的瓶的（ ）是 1.25 L。 7、将 40 L 水倒入棱长为 4 dm 的正方体鱼缸里，水面距缸边还有（ ）。 8、一个长方体长 3 dm，宽 2 dm，高 1 dm，如果高增加 1 dm，体积比原来增加（ ）。 9、把一个棱长是 a 的正方体，截成两个同样大小的长方体，这两个长方体的表面积和是 （ ）体积和是（ ）。 10、一个正方体的棱长是另一个正方体棱长的 3 倍，那么，这个正方体的体积是另一个正方 体体积的（ ）倍。 11、一个喷雾器的药箱的容积是 13 L，如果每分钟喷出药液 650 ml，喷完一箱药液需用 （ ）分钟。 12、一个长方体长扩大 2 倍，宽扩大 3 倍，高扩大 4 倍，它的体积扩大（ ）倍。 13、一个正方体的棱长扩大 2 倍，表面积扩大（ ）倍，体积扩大（ ）倍。 14、把一个长 4 ㎝，宽 2 ㎝，高 2 ㎝的长方体截成两个完全相同的正方体，表面积增加了 （ ）c ㎡,是（ ）c ㎡，它的体积是（ ）c 3m 。 15、一根方木，长是 5 dm，横截面是一个正方形，沿高锯成两段后，表面积增加了 0.32 d ㎡，原来这根方木的表面积是（ ）d ㎡，体积是（ ）d 3m 。 16、一个正方体的棱长为 a 厘米，它的棱长之和是（ ），底面积是（ ） 表面积是（ ），体积是（ ）。 17、用两个棱长是 3 ㎝的正方体拼成一个长方体，这个长方体的表面积是（ ）c ㎡，体积是（ ）c 3m 。 18、 1 立方米的正方体可以分成（ ）个１立方分米的小正方体，如果把这些小正方 体摞成一行，长是（ ）米。 19、5 升水倒入长 0.4 米，宽 0.2 米的玻璃缸中，水深（ ）米。 20、一个数的最大因数是 24，这个数的最小倍数是（ ）。 21、用质数和的形式表示：20 =（ ）＋（ ）=（ ）＋（ ）。 22、48 的因数有（ ），其中（ ）是 4 的倍数。 23、20 以内既是合数又是奇数的数是（ ），20 以内内既是质数又是偶数的数是 （ ）。 24、50 以内最大的质数与最小的合数的乘积是（ ），50 以内最大偶数除以最小质数的 商是（ ）。 25、偶数＋奇数 = （ ），奇数 + 奇数 =（ ）。 26、从 0、9、3、5 这几个数中选三个数字组成一个是 5 的倍数的最小三位数是（ ）。 27、一个三位数，有因数 2，又是 5 的倍数，百位上的数是最小合数，十位上是 10 以内最 大奇数，这个数是（ ）。 28、把 210 写成几个质数相乘的形式是（ ）。 29、98 分解质因数是（ ）。 30、□45 这个三位数，同时是 3 和 5 的倍数时，□里最大能填（ ）最小能填（ ）。 31、既是偶数又是质数的数是（ ），既是合数又是奇数的最小数是（ ）。 32、棱长 5 ㎝的正方体木块，表面积是（ ），体积是（ ）。 33、一个长方体长 10 ㎝，宽 8 ㎝，高 5 ㎝，这个长方体 6 个面中最大的面的面积是 （ ），最小的面的面积是（ ）它的表面积是（ ）， 体积是（ ）。 34、 一个长方体它的棱长之和是 64 ㎝，长是 8 ㎝，宽是 3 ㎝，高是（ ）㎝，它的底 面积是（ ） 它的表面积是（ ），它的体积是（ ）。 35、 三个连续奇数的和是 219，这三个奇数分别是（ ）、（ ）和（ ）。 36、 一个长方体木块长 6 dm，横截面是一个边长为 4 dm 的正方形，这个正方体可切成 （ ）个 1 d 3m 的小正方体。 37、 274 至少加（ ）才是 3 的倍数，至少减去（ ）才是 5 的倍数，至少加上（ ） 既是 2 的倍数，又有 5 的因数，同时还能被 3 整除。 38、 数 a 是自然数，它的最小因数是（ ），最大因数是（ ），最小倍数是（ ）。 39、 将棱长是 10 ㎝的正方体铁块熔铸成一个底面长 5 ㎝，宽 4 ㎝的长方体，这个长方体铁 块的高是（ ），表面积是（ ）。 40、 一个魔方的棱长是 9 ㎝，将魔方截去一层后，剩余形体的表面积是（ ）， 截去的体积是（ ）。 41、 5 个苹果平均分给 7 个小朋友，每个小朋友分得这些苹果的（ ），每个小朋友分 得（ ）个苹果。 42、 把一根 5 米长的绳子平均剪成 8 段，每段是这根绳子的（ ），每段长（ ） 米。 43、 7 6 米表示把 1 米平均分成（ ）份，取其中的（ ）份；或把 6 米平均分成（ ） 份，取其中的（ ）份。 44、 8 5 表示把“1”平均分成（ ）份，取其中的（ ）份，也可以表示把“5”平 均分成（ ）份，取其中的（ ）份。 45、 13 17 7 的分数单位是（ ），它含有（ ）个这样的分数单位。 46、 ( )÷25 = 5 1 = 15÷( ) = ( ) (小数)。 47、 0.875 = ( ( ) ) = ( )÷56 = 56÷( )。 48、 0.8 里面有( )个 5 1 ;有( )个 15 1 , 3 5 2 = 2 ( 1 5 ) ;1 8 1 =  3  2 49、 把 7 3 的分子加上 6,要使分数的大小不变,分母应该加上( )。 50、 6 5 表示把( )平均分成( )份,取这样的( )份。 51、 3÷4 = ( ( ) ) = ( 12 ) = ( 1 2 ) 。 52、 16 和 24 的最大公因数是( ),12、15 和 20 的最小公倍数是( )。 53、三个连续的奇数中，中间一个是 a ，最小一个是（ ），最大是（ ）。 54、 把 12 11 、 18 7 和 6 5 按从小到大的顺序排列起来是( )＜( )＜( )。 55、 2 4 3 的分数单位是( ),它含有( )个这样的分数单位,再添上( )个这 样的分数单位就等于 3。 56、 一个分数,分子与分母的和是 68,约分后是 9 8 ，原来这个分数是( )。 57、 5 3 的分数单位与 8 7 的分数单位相差（ ）。 58、 分母是 6 的所有最简真分数之和是（ ）。 59、 1 减去 5 2 与 3 1 的和，结果是（ ）。 60、 36 分 = （ ）时 61、 1－（ ）－ 8 3 = 8 1 62、 分数单位是 9 1 的所有最简真分数的和是（ ），它有（ ）个这样的分数单位。 63、 一个分数，分子与分母的和是 30，如果分子加上 8，这个分数就等于 1，这个分数是 （ ）。 64、 一本故事书，小林已经看了全书的 5 2 ，还剩下全书的（ ）没看。 65、 7 3 和 9 5 的（ ）不同，所以不能直接相减，必须先（ ）再相减。 66、 一批水泥，第一次用去总数的 9 2 ，第二次用去总数的 3 1 ，还剩下总数的（ ）。 67、 分数单位是 9 1 的最小真分数与最大真分数的和是（ ），差是（ ）。 76、妈妈今年 26 岁，是小玲年龄的 13 倍，（ ）年后，妈妈的年龄是小玲的 7 倍。 77、在自然数中，最小的奇数是（ ），最小的质数是（ ），最小的合数是（ ）。 78、一个数的倍数的个数是（ ），最小的倍数是（ ），一个数的因数个数是 （ ），最大的因数是（ ）。 79、一个两位数，既是 3、5 的倍数，又有因数 2，这个两位数最大是（ ）。 80、7 除以 11 的商用分数表示是（ ），它的分数单位是（ ）。 81、把 11 米长铁丝平均分成 9 份，5 份是它的（ ），5 份长（ ）米。 82、把 6 1 的分子加上 3，要使分数的大小不变，分母应加上（ ）。 83 、 4 3 =  6  =  1 2  =  1 8  =  3 6  =( ) ÷ ( )=( )(小数)。 84、一个分数是 5 x ，当 x（ ）时，这个分数是假分数，当 x（ ）时，这个分数是 真分数，当 x （ ）时，这个分数等于 0。 85、把 4 3 ， 9 1 ，0.9， 12 5 按从大到小的顺序排列是（ ）。 86、 1 路车每 5 分钟发一次车，2 路车每 4 分钟发一次车。如果这两路公共汽车同时出站， 至少过（ ）分钟它们又同时发车。 88、一个长方体，长、宽、高都扩大 2 倍，体积扩大（ ）倍，表面积扩大（ ） 倍。 89、把一个棱长为 2 分米的正方体，切成两个相等的长方体，每个长方体的体积是 （ ），表面积是（ ）。 90、在三角形、正方形、长方形和圆中，对称轴最多的是（ ）。 91、挖一个长 8 米，宽 4 米，深 2 米的蓄水池，它的占地面积是（ ），可蓄水（ ） 升。 94、同时是2、3倍数的最小两位数是（ ），同时是2、3、5倍数的最小三位数是（ ）。 95、三个连续偶数的和是 42，这三个偶数分别是（ ）、（ ）和（ ）。 96 、 用 一 根 长 48 厘 米 的 铁 丝 制 成 一 个 正 方 体 框 架 ， 这 个 正 方 体 的 表 面 积 是 （ ）。 97、 1500ml = ( ) L 456 立方分米 =（ ）升 58.07 立方米 =（ ）立方分米 =（ ）立方厘米 98 、 在 自 然 数 1 ～ 10 中 ， 质 数 有 （ ） 合 数 有 （ ）。 99、12 和 15 的最大公因数是（ ），最小公倍数是（ ）。 100 、 把 1 4 1 、 9 5 、 1.75 和 8 15 按 从 大 到 小 的 顺 序 排 列 是 （ ）。 101、一个长方体的金鱼缸，长是 8 分米，宽是 5 分米，高 6 分米，前面的玻璃不小心被打 破了，修理时配的玻璃的面积是（ ）。 102、一个正方体的棱长总和是 72 厘米，它的表面积是（ ），体积是 （ ）。 103、三个不同质数的积是 385、这三个质数分别是（ ）、（ ）和（ ）。 104、正方体可以看作是（ ）的长方体。 105、把 5 米长的铁丝平均分成 8 段，每段占全长的（ ），每段的长度是（ ）。 106、能同时被 2、3、5 整除的最小三位数是（ ），最大三位数是（ ）。 107、一个数的最小倍数是 12，这个数的最大因数是（ ）。 108、一个底面为正方形的长方体，高是 20 厘米，侧面展开后刚好是个正方形，这个长方体 的表面积是（ ）平方厘米，体积是（ ）立方厘米。 109、两个都是质数的连续自然数是（ ）和（ ）。 110、一个正方体的体积是 27 立方厘米，它的棱长（ ），表面积是（ ）。 111、一个长方体的体积是 30dm3,长是 6dm，高是（ ）。 112、 a 8 （ a 为非 0 自然数），当 a （ ）时，它是真分数，当 a （ ）时， 它是假分数。 113、一个底面为正方形的长方体的体积是 100 立方分米，高是 4 分米，它的表面积是 （ ）分米。 114、甲数 = 2×2×3×7，乙数= 2×3×5，甲、乙两数的最小公倍数是（ ），最大公因数 是（ ）。 115、用（ ）个棱长 1 ㎝的小正方体可以拼成一个长 8 ㎝，宽 6 ㎝，高 4 ㎝的长方体。 五年级数学多边形面积常错经典题 一、填空（每空 1 分，共 13 分） 1．一个平行四边形的底是 14 厘米，高是 9 厘米，它的面积是（ ）；与它等底等高 的三角形面积是（ ）. 2．工地上有一堆钢管，横截面是一个梯形，已知最上面一层有 2 根，最下面一层有 12 根， 共堆了 11 层，这堆钢管共有（ ）根。 3．一个三角形比与它等底等高的平行四边的面积少 30 平方厘米，则这个三角形的面积是 （ ）。 4．一个三角形的面积是 4.5 平方分米，底是 5 分米，高是（ ）分米。 5．一个等边三角形的周长是 18 厘米，高是 3.6 厘米，它的面积是（ ）平方厘米。 二、判定题（每题 2 分，共 10 分） 1．两个面积相等的三角形，一定能拼成一个平行四边形.（ ） 2．平行四边形的面积等于一个三角形面积的 2 倍.（ ） 3．两个完全一样的梯形，能拼成一个平行四边形.（ ） 4．把一个长方形的框架挤压成一个平行四边形，面积减少了.（ ） 5．两个三角形面积相等，底和高也一定相等。（ ） 三、选择题（每题 2 分，共 8 分） 1．等边三角形一定是 _______ 三角形.[ ] A．锐角； B．直角； C．钝角 2.两个完全一样的锐角三角形，可以拼成一个 ________[ ] A．长方形； B．正方形； C．平行四边形； D．梯形 3．把一个平行四边形任意分割成两个梯形，这两个梯形中 ________总是相等的.[ ] A．高； B．面积； C．上下两底的和 四、填空。 1．在推导平行四边形面积计算公式时，可把平行四边形通过割补平移转化为( )形去 推导，推导三角形面积计算公式时，可把两个完全一样的三角形拼成一个( )形去推 导，推导梯形面积计算公式时，可把两个完全一样的梯形拼成一个( )形进行推导。 2．直角三角形的两条直角边长分别为 3 厘米和 4 厘米，这个直角三角形面积是( )平方厘 米。 3．一个三角形的底边长扩大 2 倍，高不变，扩大后的三角形面积比原来三角形面积扩大( ) 倍。 五、判断题。 1．平行四边形面积等于长方形面积。( ) 2．等底等高的三角形可拼成一个平行四边形。( ) 3．只要知道梯形的两底之和的长度和它的高，就可以求出它的面积。( ) 4．两个周长相等的等边三角形，面积必相等。( ) 一、填空。 1.一个三角形的面积是 25 平方厘米，和它等底等高的平行四边形的面积是 ( )平方厘米。 2.平行四边形的底长 16 米，高是 12 米，它的面积是（ ）平方米。 3.在一个长 9 厘米，周长 26 厘米的长方形内画一个最大的三角形，这个三角形的面积是 ( )平方厘米。 4.三角形的底扩大 3 倍，高扩大 2 倍，面积扩大（ ）倍。 5.一个三角形与梯形的高相等，它们的面积也相等。那梯形的上底与下底的和等于三角形 ( )的长度。 6.右图中阴影部分的面积是 15 平方厘米，长方形的 面积是( )平方厘米。 7..一个平行四边形的底是 6 厘米，高是 14 厘米，它的面积是（ ）平方厘米，与它等底等 高的三角形面积是（ ）平方厘米。 8.如图，每个方格的边长为 1 厘米，这只小鱼的面积是（ ）平方厘米。 9.有一个长方形长 15 厘米，宽 8 厘米，另一直角梯形上底长 7 厘米，下底长 6 厘米，高 8 厘米，将它们拼成一个梯形，梯形的面积是( )平方厘米。 10.一个平行四边形，底为 10 分米，高是 4 分米，如果底不变，高增加 2 分米，则面积增加 （ ）平方分米；若高不变，底增加 2 分米，则面积增加（ ）平方分米。 11.将木条订成的长方形后拉成一个平行四边形（如图），原来长方形的面积是（ ）平方厘 米，现在平行四边形的面积是（ ）平方厘米，现在平行四边形的周长是（ ）厘米。 二、判断。 1.梯形的面积比平行四边形的面积小。（ ） 2.梯形的上底一定比下底短。（ ）： 3.两个三角形的高相等，面积不一定相等。（ ） 4.任意两个三角形都能拼成平行四边形。（ ） 5.把一个平行四边形分成两个三角形，这两个三角形一定完全相同。（ ） 6.两个完全一样的直角梯形可以拼成一个长方形。（ ） 7.周长相等的长方形和平行四边形的面积相等。（ ）： 8.等底等高的两个平行四边形的面积相等。（ ）； 9.把一个平行四边形分成两个完全一样的梯形，这两个梯形的高一定相等。( )： 三、精挑细选。 1.一个平行四边形底缩小 10 倍，高扩大 10 倍，这个平行四边形的面积( )。 A.大小与原来相等 B.缩小 10 倍 C.扩大 10 倍 2.将一个长方形拉成一个平行四边形（四条边长度不变），它的面积( )。 A.比原来小 B.比原来大 C.与原来相等 3.两个完全一样的直角三角形，不可能拼成一个（ ）。 A.梯形 B.正方形 C. 三角形 4.梯形有（ ）条高。 A.无数 B.2 C. 1 5.把三根同样长的铁丝分别围成长方形，正方形和平行四边形，围成图形的面积，（ ）。 A.正方形大 B.长方形大 C.平行四边形大 8.在面积为 42 平方米的平行四边形内画一个最大 的三角形，这个三角形的面积是（ ）。 A.21 B. 30 C.14 五、解决问题。 2.一堆木头整齐地叠放在地上，最下一层有 25 根，最上一层揩油 6 根，一共叠放了 20 层。 每下面一层都要比它上面一层多一根。这堆木头一共有几根？ 3.一张梯形的纸片，下底是 24 厘米，上底是 18 厘米，高 14 厘米，把它剪成一张尽可能大 的三角形纸片，求余下的碎纸屑的总面积。 7.用一张长 12 分米、宽 4 分米的长方形纸，裁成直角边是 4 分米的等腰三角形，共可以裁 成几张？ （1）、三角形的面积等于底乘以高。（ ） （2）、两个三角形可以拼成一个平行四边形。（ ） （3）、一个三角形的面积是 24 平方米，高 8 米，底是 3 米。 （ ） （4）、两个完全一样的三角形拼成的平行四边形，它的底和高与三角形分别相等。（ ） （5）、三角形的面积是平行四边形面积的一半。（ ） （6）、一个三角形的高是 4 厘米，底是 5 厘米，面积是 4×5÷2=10（厘米）。（ ）新课 标 第一 网 “图形面积（一）”单元练习 一、填空 （1）一个平行四边形，底边是 5.7 米，面积是 26.22 平方米，高是（ ）米。 （2）一个三角形和一个平行四边形等底等高，如果平行四边形的面积是 128 平方米，那 么三角形的面积是（ ） （3）一个梯形，上底是 3.4 厘米，下底是 4.8 厘米，高是 2.7 厘米，则这个梯形的面积是 （ ）xkb 1.co m （4）一个平行四边形的底是 2.4 分米，高是底的一半，它的面积是（ ） （5）一个三角形的底是 0.4 米，是高的 2 倍，它的面积是（ ） （6）一个正方形的周长是 16 厘米，它的面积是（ ）平方厘米。 （7）一个梯形的上底是 4.5 厘米，下底是 5.2 厘米，高是 5 厘米，它的面积是（ ）平方 厘米。 （8）一个面积是 6.3 平方米的梯形，上底是 1.4 米，高是 1.2 米，下底是（ ）米。 二、判断（对的画“√”，错的画“×”） （1）平行四边形只有一条高。 （ ） （2）两个面积相等的三角形可以拼成一个平行四边形。 （ ） （3）等底等高的三角形，面积一定相等。 （ ） （4）平行四边形的面积一定比三角形的面积大。 （ ） a （5）右图是贝贝做的三角形 a 边上的高。 （ ） h 三、选择 （1）把一个平行四边形割补成一个长方形后，面积不变，周长（ ）。 A．扩大了 B．缩小了 C．不变 （2）梯形的上底 CD 在不停地变化。当 CD 的长等于零时， D C 这个图形就变成了（ ）；当 CD 长和 AB 长相等时，这个图 形就变成了（ ）。 A B A．三角形 B．长方形 C．平行四边形 （3）面积是 56 平方分米的平行四边形，底是 14 分米，高是（ ）。 A．4 分米 B．2 分米 C．8 分米 （4）用字母表示图中阴影部分的面积是（ ）。 A． ah B．ah+ ah C．ah （5）一个平行四边形，底边不变，高扩大 3 倍，它的面积（ ） A．扩大 3 倍 B．扩大 9 倍 C．缩小 3 倍 （6）设为一个三角形的面积是 63 平方分米，高是 7 分米，它的底是（ ） A．4.5 B．18 C．9 （7）把一个平行四边形任意分割成两个梯形，这两个梯形中（ ）总是相等的。 A．高 B．面积 C．上下两底的和 （8）一个三角形，底不变，高扩大 5 倍，它的面积（ ）。 A．扩大 5 倍 B．扩大 25 倍 C．缩小 25 倍 （9）两个（ ）的梯形可以拼成一个平行四边形。 A．面积相等 B．周长相等 C．等腰梯形 D．完全相同 四、超级变变变 图 形 底（cm） 高（cm） 面积（cm2） 长方形 8 6.5 平行四边形 7.5 60 4.3 25.8 三角形 10.2 5.8 24 150 梯 形 上 4.2 下 6.7 54.5 五、动手做：测量出相关数据并计算面积。 六、聪明会馆 一个三角形苗圃，底长 80m，高 35m，在圃中栽种菊花苗，每棵菊花苗占地 0.2 平方米， 这块花圃共需多少棵菊花苗？ 人教版五年级数学下册思维训练测评 班级__________ 姓名__________ 学号__________ 1． 小明期末考试时，语文，数学两科的平均分是 95 分，数学比语文少 8 分， 张明的语文，数学各是多少分？ 2． 有甲，乙两箱苹果共 85 千克，从甲箱里取出 5 千克苹果放入乙箱里，甲箱 还比乙箱多 3 千克。甲箱原有苹果多少千克？ 3． 把右图的长方体分割成两个棱长是 4CM 的正方形，两个正方体的总面积与 长方体的表面积相差多少？ 4.有两个正方形水池，它们的内边长分别是 4 米，3 米。把一堆碎石放在小水池 里，水面升高 4 厘米，如果把这堆碎石放在大水池，水面升高多少厘米？ 4CM 8CM 4 C M 5．4 7 的分子加上 12，要使分数的大小不变，分母应加上（ ），若是分母加 上 70，要使分数的大小不变，分子应加上（ ）。 6．分子说：“我和分母不相等且都是奇数。”分母说：“我俩的和是 30。”它们组 成的分数最大是（ ），最小的是（ ）。 8．一个分数，加上它的一个分数单位后是 1，减去它的一个分数单位后是7 8 ， 这个分数是（ ）。 9．学校进行书法比赛，设有一，二，三等奖。获一，二，等奖的占获奖人数的3 8 ， 获二，三等奖的占获奖人数的7 8 。获二等奖的占获奖人数的几分之几？ 10．一个旅行社有 36 人，其中会英语的有 24 人，会法语的有 18 人，两样都不 会的有 4 人，两样都会的有多少人？ 11．上学期期末检测，五（1）班 47 名学生参加的数学和语文检测，其中语文 得 100 分的 12 人，数学得 100 分的 17 人，两门都没有得 100 分的有 26 人。问： 两门都得 100 分的有多少人？ww 12．甲，乙，丙，丁四个小孩子踢球时不小心打碎了玻璃。甲说：“是丙或丁打 碎的”。乙说：“是丁打碎的”。丙说：“我没有打碎玻璃”。丁说：“不是我打碎的”。 他们中只有一个人说了慌，应该是（ ）打碎了玻璃。 13．盒里装着各色圆珠笔，其中红色占1 4 ，后来又往盒里放了 8 支红色圆珠笔， 这时红色圆珠笔占总数的 5 12 ，则原有红色圆珠笔（ ）支。 14．一个合唱队共有 50 人，寒假期间有一个紧急演出，老师需要尽快通知到每 一个队员，如果用打电话的方式，每分钟通知 1 人，最少花（ ）分钟能通知 到每一个人。 15．小军和妈妈现在年龄的和是 36 岁，3 年后，妈妈比小军大 26 岁，今年小军 和妈妈各多少岁？ 16．有 19 瓶水，其中有 18 瓶质量相同，另有一瓶是盐水，比其他的水稍微重 一些，至少称（ ）次保证找出这瓶盐水。 17．五（2）班有 40 人，许多人参加课外小组，参加美术小组的有 12 人，参加 奥数组的有 30 人，两个组都没参加的有 4 个人，既参加美术组又参加奥数组的 有多少人？ 新课标 第一网 18．奇数+偶数=（ ） 奇数+奇数=（ ） 偶数+偶数=（ ） 19．有 2 个质数，它们的和是 10，积是 21。这两个质数是（ ）、（ ）。 有 2 个质数，它们的和是 20，积是 91。这两个质数是（ ）、（ ）。 20．正方体的六个面分别写着 A、C、D、E、F、I。与 A、E、I 相对的面分别是 （ ）、（ ）、（ ）。 21. 36 可能是哪两个数的最小公倍数？你能找出几组? X kb1. c om 22.父亲 45 岁.儿子 23 岁.问几年前父亲年龄是儿子的 2 倍？ 23.李老师的年龄比刘红的 2 倍多 8 岁，李老师 10 年前的年龄和王刚 8 年后的年 龄相等.问李老师和王刚各多少岁？ A E I F I A C I F 24.姐妹两人三年后年龄之和为 27 岁，妹妹现在的年龄恰好等于姐姐年龄的一半， 求姐妹二人年龄各为多少. 25.大熊猫的年龄是小熊猫的 3 倍，再过 4 年，大熊猫的年龄与小熊猫年龄的和 为 28 岁.问大、小熊猫各几岁？ 26.前年红红和姐姐的年龄加起来正好 30 岁，今年红红和姐姐的年龄之和为多少 岁？ 27.一家三口人，三人年龄之和是 74 岁，妈妈比爸爸小 2 岁，妈妈的年龄是儿子 的 4 倍，问三人各是多少岁？ 28.47 名学生参加了数学和语文考试，其中语文得 100 分的 12 人，数学得 100 分的 17 人，两门都没得 100 分的有 26 人。问：两门都得 100 分的有多少人？ 29.全班有 46 名同学，仅会打乒乓球的有 18 人，会打乒乓球又会打羽毛球的有 7 人，不会打乒乓球又不会打羽毛球的有 6 人。问：仅会打羽毛球的有多少人？ 30.电视台向 100 人调查昨天收看电视情况，有 62 人看过 2 频道，34 人看过 8 频道，11 人两个频道都看过。问：两个频道都没看过的有多少人？ 31.一次数学小测验只有两道题，结果全班有 10 人全对，第一题有 25 人做对， 第二题有 18 人做错，那么两题都做错的有多少人？ 32.六一儿童节那天，全班 45 人到颐和园去玩，有 33 人划了船，20 人爬了山， 5 名同学因身体不好，他们既没划船也没爬山，他们游览了长廊。问：既划了船 也爬了山的同学有多少？ 33.全班 50 人，不会骑自行车的有 23 人，不会滑旱冰的有 35 人，两样都会的有 4 人。求两样都不会的人数。 34.五一小学举行小学生画展，其中 18 幅不是六年级的，20 幅不是五年级的。 现在知道五、六年级共展出 22 幅画，问：其它年级共展出多少幅画？ 长方体和正方体错题总集 一．填空题。 1．0.08 立方米=（ ）升=（ ）毫升 3.8 升=（ ）升（ ）毫升 6.47 升=（ ）毫升=（ ）立方分米 415 平方厘米=（ ）平方米 10020 立方分米=（ ）立方米 20 升=（ ）立方米 9．08 立方分米=（ ）升=（ ）毫升 0.08 立方米=（ ）毫升 2.一个长方体，长是 3m，宽和高都是 0.5m，把它分割成两个完全一样的小 长方体，表面积最少增加（ ）平方分米。 3.至少要（ ）小正方体才能拼成一个长方体。如果小正方体的棱长是 5cm， 那么大正方体的表面积是（ ）平方厘米，体积是（ ）立方分米。 4.把一长 124cm，宽和高都是 10cm 的长方体锯成最大的正方体，最多可以 锯（ ）个 5.用一根 12 分米长的铁丝未成一个最大的正方体框架，这个正方体的体积是 （ ）。 6.一个长方体的长宽高都扩大 3 倍，它的表面积就（ ）。 7.写出下列各式的结果。 5*5= a*a*a= b+b+b= 7x*x= 8.一个正方体的表面积是 54 平方米，它的每个面的面积是（ ），它的 棱长是（ ）。 9.一个正方体的棱长扩大到它的 4 倍，它的体积就（ ），它的表面积 就（ ）。 10.一个长方体相交于一个顶点的三条棱分别是 5cm，3cm，4cm，这个长方体 的所有棱长之和是（ ）厘米，体积是（ ）。 二．判断题。 （ ）1.棱长是 6cm 的正方体，体积和表面积相等。 （ ）2.体积相等的两个正方体，它的表面积也一定相等。 （ ）3.一个棱长为 5 的无盖正方体，它的表面积是 500 平方米。 （ ）4.长方体的三条棱分别叫长，宽，高。 （ ）5.有两个相对面是正方形的长方体，它的其余四个面完全相同。 （ ）6.至少用 4 个体积是 1 立方厘米的正方体，才能拼成一个大正方体。 （ ）7.长方体中有时四个面是完全一样的长方形。 （ ）8.冰箱的体积就是冰箱的容积。 （ ）9.一个长方体横着或竖着放时所占的空间不一样大。 （ ）10.正方体是长宽高都相等的特殊的长方体。 三．应用题。 1.一根长 2 米的长方体木料锯成两段后，表面积增加了 100 平方厘米，它的 体积是多少？ 2.一个长方体正好可以切成两个棱长是 3 厘米的正方体，这个长方体的表面 积是多少？ 3.学校要漆一道长 20 米，宽 0.24 米，高 2 米的墙，每立方米需要砖 525 块， 学校需要买多少块砖？ 4.有一块棱长是 80cm 的正方体的铁块，现在把它熔铸成一个横截面是 20 平 方厘米的长方体，这个长方体的体积是多少分米？ 5.在一个长 10 米，宽 3.5 米的长方体客厅的地面上铺设 2 厘米厚的木地板， 至少需要木材多少立方米？铺好再涂上油漆，油漆面积是多少？ 6.三个同样大的正方体拼成一个长方体后，表面积减少了 144 平方厘米，这 个长方体的表面积是多少？ 7.3 个棱长都是 8 厘米的正方体，拼成一个长方体，表面积是多少？ 8.把一个棱长是 8 厘米的正方体钢，锻造成长 16 厘米，宽 5 厘米的长方体钢 板，钢板有多厚？ 9.一根方木，底面是边长 8 厘米的正方体，从方木上截下体积是 1.28 立方分 米的一段，应该截多长？ 10.在一个长 120 厘米，宽 60 厘米的长方体水箱里，放入一块长方体的铁块 后，水面比原来上升了 2 厘米，已知铁块的长和宽都是 20 厘米，求铁块 的高？ 11.把一个棱长是 8 厘米的正方体铁块放入一个长 32 厘米，宽 16 厘米，水 深 4 厘米的长方体水池中，水面上升多少厘米（精确到 0.01）？ 12.两个大小相同的正方体拼成一个长方体，已知长方体的棱长总和是 48 厘 米，那么，每块正方体的体积是多少？ 13.一长方体游泳池，长 40 米，宽 14 米，深 1.2 米，要在四壁上贴上边长是 4 厘米的正方形需要多少块？ 14.已知一个长方体的长宽高分别是 8 厘米，5 厘米，4 厘米，制作这样一个 长方体框架，至少需要多少铁丝？如要包装，需要多少包装纸？ 15.一个底面是正方形的长方体，所有棱长的和是 100 厘米，它的高是 7 厘 米，这个长方体的体积是多少立方厘米？ 长方体、正方体提高卷 姓名:________ 班级：_________ （注意：字体写工整，分版块书写） （1）王老师做了一个长方体教具，长是 6 厘米，宽是 3 厘米，高是 4 厘米，这 个长方体教具的表面积是多少平方厘米？ （2）用一根 48 厘米长的铁丝焊接成一个正方体模型，这个正方体模型的棱长是 多少厘米？ （3）一个正方体木块，把它锯成两个完全一样的长方体后，每个长方体的表面 积比原来正方体的表面积小 32 平方厘米。求原正方体的体积。 （4）一个长方体的长和宽相等，都是 4 厘米。如果将高去掉 2 厘米，这个长方 体就成为一个正方体，原来长方体的体积是多少立方厘米？ （5）将 200 升水倒入一个长 1 米，宽 5 分米，高 6 分米的鱼缸内，水面离鱼缸 口有多少？ （6）把两块棱长 2 分米的正方体木块粘成一个长方体，这个长方体的表面积是 多少平方分米？ （7）一根长 42 分米的铁丝做一个正方体框架，这个正方体框架的棱长是多少分 米？ （8）将三个棱长是 5 厘米的小正方体木块拼接成一个大的长方体，拼接成的长 方体的表面积是多少平方厘米？ （9）一个长方体和一个正方体的棱长之和相等，已知长方体的长、宽、高分别 是 6 分米、4 分米、26 分米，正方体的体积是多少立方分米？ （10）一个长 2 分米，宽 4 分米，高 5 分米的长方体木块，这个木块的体积是 多少立方分米？ （11）一种长方体卫生箱，长 4 分米，宽 2.5 分米，高 2 分米，做这样一个卫生 箱至少用多少平方分米的木板？ （12）一个正方体玻璃容器的棱长是 15 厘米，这个玻璃容器的表面积是多少平 方厘米？体积是多少立方厘米？ （13）用 1.04 米长的铁丝做一个长方体模型，这个长方体模型的长 12 厘米，宽 8 厘米，高是多少厘米？ （14）一个长方体油箱，容积是 20 升，这个油箱的底面是个边长为 20 厘米的 正方形。油箱的高是多少厘米？ （15）一个教室的长是 9 米，宽是 6 米，高 4 米。要粉刷教室的屋顶和四面墙 壁，除去门窗和黑板面积的 22.4 平方米，粉刷的面积是多少平方米？ （16）用铁皮密封的水箱长 6 米，宽 4 米，深 5 米。在它四周和底面刷防锈漆， 每平方米需防锈漆 0.6 千克，共需用防锈漆多少千克？（厚度不计） （17）一个棱长 4 分米的正方体水箱，里面有 2 分米的水，现在把一个石头放在 水中，水面升高 1 分米，石头的体积是多少立方分米？ （18）一个零件形状大小如下图：算一算，它的体积是多少立方厘米，表面积是 多少平方厘米？（单位：厘米） （19）有一个形状如下图的零件，求它的体积和表面积。（单位：厘米） 2 2 24 2 6 （20）有一个长 8 厘米、宽 1 厘米、高 3 厘米的长方体木块，在它的左右两角各 切掉一个正方体（如图），求切掉正方体后的表面积和体积各是多少？ 4 6 10 2 2 1 1 1 1 （21）把 27 块棱长是 1 厘米的小正方体堆成一个大正方体，这个大正方体的表 面积比原来所有的小正方体的面积之和少多少平方厘米？ （22）18 个边长为 2 厘米的小正方体堆成如图的形状，求它的表面积。 （23）有一个长方体，长 10 厘米，宽 6 厘米、高 4 厘米，如果把它锯成棱长是 1 厘米的小正方体，一共能锯成多少个？这些小正方体的表面积和是多少？ （24）把棱长是 12 厘米的正方体的铁块，锻造成宽和高都是 4 厘米的长方体的 铁条，锻造的铁条长多少厘米？ （25）一个长方体的花坛，体积是 60 立方米，高是 0.3 米。这个花坛占地面积 是多少平方米？ （26）一块长方体的钢板长 2.5 米，宽 1.2 米，厚 20 厘米。这种钢板每立方分 米重 7.8 千克，这块钢板重多少千克？ （27）一块长 6 米，宽 18 分米，厚 9 分米的长方体木块，可以截出多少块棱长 是 3 分米的正方体？ （28）一个正方体油箱，容积是 216 立方分米，把这一箱油倒入另一个长方体油 箱内。已知长方体油箱长 8 分米，宽 5 分米，这个油箱中油深多少分米？ （29）要挖一个容积是 4.8 立方米的长方体地窖，如果地窖的长是 2 米，宽是 1.2 米，深要挖几米？ （30）一个长方体水池，长 12 米，宽 5 米，里面水深 120 厘米，如果 1 立方米 重 1 吨，这个水池里的水是多少吨？ （31）把两块棱长 1.5 分米的正方体木块粘成一个长方体，这个长方体的体积和 表面积各是多少？ （32）把一个棱长是 10 厘米的正方体木块，锯成两个长方体木块，它的表面积 可增加多少？ （33）把两个棱长是 5 分米的正方体木块，拼成一个长方体，这个长方体的表面 积是多少平方分米？ （34）一个正方体，表面积是 24 平方分米，把它平均分成两个长方体，每个长 方体的表面积是多少平方分米？ 错题订正栏： 第二学期五年级几何达标测试题 一、填一填（30 分）。 1、一块橡皮的体积约是 6（ ）。 教室地面面积约是 48（ ）。 2、长方体有（ ）个顶点，有（ ）条棱，有（ ）个面，每个面都是（ ）形， 可能有（ ）个相对的面是正方形。 3、一个三角形，底 2 厘米，高 5 厘米，它的面积是（ ）平方厘米。 4、一个等腰三角形，其中两条边的长度分别是 7cm 和 14cm，这个三角形的周长是 ( )cm. 5、用铁丝焊接成一个长 20 厘米，宽 15 厘米，高 8 厘米的长方体的框架，至少需要铁丝 （ ）厘米，给这个长方体框架糊上彩纸，需要（ ）的彩纸。体积 ( )。 6、在一个三角形 ABC 中，∠A=40°，∠B=80°， ∠C=（ ）。 7、如图一个平行四边形的高为 5 厘米，则它的面积是（ ）平方厘米。 8、一个正方体切成两个长方体后表面积增加了 98 平方厘米，原来正方体的表面积是 （ ）平方厘米。 5cm 6cm 二、选一选（ 10 分 ）。 1、钟面上 3：30 时，时针与分针所成的角是（ ）。 A. 锐角 B. 直角 C.钝角 D 平角 2、用棱长 2cm 的小立方体木块拼成一个稍大立方体，至少需要这样的小立方体（ ） 块。 A. 4 B. 16 C. 8 D. 9 3、一个三角形的最小内角是 46 度，这个三角形一定是（ ） A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 无法确定 4、下面每组三条线段，不能围成三角形的是（ ）。 A．1 分米 5 厘米 0.07 米 B．14 厘米 13 厘米 2 厘米 C．9 米 7 米 5 米 D． 6 厘米 9 厘米 3 厘米 5、一个平行四边形和一个三角形等底等高，已知平行四边形的面积是 60 平方厘米，那么 三角形的面积是（ ）平方厘米。 A 30 B 120 C 25 D 60 三、判一判（10 分） 1、用长度分别是 10、6 和 5cm 的三根小棒，头尾相连，一定能摆出一个三角形。（ ） 2、如果一个三角形有两个内角是锐角，它一定是锐角三角形。（ ） 3、小华画了一条 4 厘米长的直线。（ ） 4、一个正方体的棱长总和是 24 厘米，则它的表面积是 24 平方厘米。 （ ） 5、边长是 2cm 的正方形的周长和面积是相等的。 （ ） 四、算一算（ 26 分 ） 1、寻找合适的条件，求出各图形的面积。（单位：米）（9 分） 2、求下面各图形的面积。（单位：分米）（9 分） 3、计算下面图形的表面积和体积（8 分） 五、解决问题。（24 分） 1、右图是一块梯形菜地的示意图。王大伯把它分成一个平行 四边形和一个三角形，平行四边形地里种白菜，三角形地里 种萝卜。 （1） 萝卜地有多少平方米？ (2) 每棵大白菜占地 16 平方分米，一共可以种多少棵？ 2、一个长方体，长 6cm，宽 5cm，高 4cm，如果把它锯成一个最大的正方体，体积比原来减 少了多少立方厘米？ ww w.xk b1.c om 3、 2008 年 5 月 12 日，汶川发生了里氏 8.0 级地震，震后政府给李梅家新分了一套住房， 客厅长 6m，宽 3m，高 3m。李梅这样装修客厅： （1）地面铺边长为 0.6m 的方砖。请你算一算，李梅至少要买多少块这样的方砖？ （2） 用乳胶漆粉刷四周墙面（扣除 10 平方米的门窗面积），每平方米大约需要 1.2kg。 李梅至少要买多少千克乳胶漆？ 应用题专项复习（长方体、正方体） 1、一根 2 米长的通风管，横截面是直径为 2 分米的圆，制作这个通风管至少需 要铁皮多少平方分米？ 2、把一个体积为 80 立方厘米的铁块浸在底面积为 20 平方厘米的长方体容器中， 水面高度为 10 厘米，如果把铁块捞出后，水面高多少？ 7米 12米 3、 要制作 12 节长方体的铁皮烟囱，每节长 2 米，宽 4 分米，高 3 分米，至少 要用多少平方米的铁皮？ 4、小敏房间的地面是长方形。长 5 米、宽 3 米，铺设了 2 厘米厚的木地板，至 少需要木材多少立方米？ 5、一辆运煤车从里面量长 2.5 米、宽 1.8 米，装的煤高 0.6 米，平均每立方米 煤重 1.5 吨，这辆车装的煤有多少吨？ 6、一种无盖的长方体形铁皮水桶，底面是边长 4 分米的正方形，高 1 米。做一 只这样的水桶至少要多少铁皮？这只水桶能装水多少升？ 7、体育场用 37.5 立方米的煤渣铺在一条长 100 米、宽 7.5 米的直跑道上。煤渣 可以铺多厚？ 8、一个长方体形状的儿童游泳池，长 40 米、宽 14 米，深 1.2 米。现在要在四 壁和池底贴上面积为 16 平方分米的正方形瓷砖，需要多少块？ 9、一个长方体的容器，底面积是 16 平方分米，装的水高 6 分米，现放入一个体 积是 24 立方分米的铁块。这时的水面高多少？www. xkb1 .co m 10、用 2100 个棱长是 1 厘米的正方体堆成一个长方体，它的高是 10 厘米，长和 宽都大于高。它的底面周长是多少？ 11、一块长方形铁皮，长 32 厘米，在它四个顶角分别剪去边长 4 厘米的正方形， 然后折起来焊成一个无盖的长方体铁皮盒。已知这个铁皮盒的容积是 768 立方厘 米。原来这块铁皮的面积是多少？ 12、一个长方体玻璃缸，底面积是 200 平方厘米，高 8 厘米，里面盛有 4 厘米深 的水，现在将一块石头放入水中，水面升高 2 厘米。这块石头的体积是多少立方 厘米？ 五下第四单元易错题整理 一、填空。 1、4/5 米是把（ ）米平均分成（ ）份，表示其中的 4 份；也可以看做 把 4 米分均分成（ ）份，表示其中的（ ）份。 2、8/11 的分数单位是（ ），再添（ ）个这样的分数单位就是最小的假分数。 3、分数单位是 1/7 的最小真分数比最小假分数少（ ）个这样的分数单位， 分数单位是 1/12 的最小带分数是（ ）。 4、一本故事书，15 天读完，平均每天读这本书的（ ），8 天读这本书的（ ）。 5、把 5 千克的西瓜平均分给 8 个人吃，平均每人吃了这个西瓜的（ ），平均 每人吃（ ）千克西瓜。 6、小学生做一次眼保健操大约需 5 分钟，每天要做两次，每天做眼保健操的时 间大约占 1 小时的（ ）。 7、在 a/5 中，a 是不为 0 的自然数，当 a 是（ ）是，它是真分数，当 a 是 （ ）时，它是假分数，当 a 是（ ）时，它可以化成整数？当 a 是（ ） 时，化成的带分数最小。 8、“小明看完一本故事书用了 2/3 小时。”这里把（ ）看做单位“1”，平 均分成（ ）份，（ ）占这样的（ ）份。 9、把 3 千克糖果平均分装在 5 个瓶子里，每个瓶子装了（ ）千克糖果，每 个瓶子装了这些糖果的（ ）。 10、一个正方体的骰子六个面分别标有 1、2、3、4、5、6。现将这个骰子任意 地投掷，掷的奇数朝上的次数约占（ ），掷得素数朝上的次数约占（ ）， 掷得既不是奇数又不是合数的数朝上的次数约占（ ）。 11、从甲地到乙地快车要行 3 小时，慢车要行 5 小时，快车每小时行全程的（ ）， 慢车每小时行全程的（ ）。 12、修一条公路，已经修的长度是未修的 5 倍，已经修了全长的（ ），还剩 全长的（ ）没有修。 13、“一根水管长 9/10 米”，这里把（ ）看做单位“1”，平均分成了（ ） 份，（ ）有这样的（ ）。9/10 的分数单位是（ ），它有（ ）这样 的分数单位，再增加（ ）个这样的分数单位是最小的合数。 14、有 12 个玩具，平均分给 6 个小朋友，每个玩具是玩具总数的（ ），每个 小朋友分得的玩具是玩具总数的（ ）。 15、把 3 米长的木料分均截成 5 段，其中 2 段占总长的（ ），每段长（ ）米。 16、在括号里填上合适的分数。 9 厘米=（ ）米 750 平方米=（ ）公顷 17 时=（ ）日 1.2 小时=（ ）小时 8.36 吨=（ ）吨 7 升 60 毫升=（ ）升 17、一个带分数，它的分数部分的分子是 6，把它化成假分数的分子是 30.这个 带分数可能是（ ）。 18、把下面的复名数先改写成分数，再改写成小数。 7 吨 250 千克=（ ）吨（ ）吨 3 日 12 时=（ ）日=（ ）日 80 平方米 70 平方分米=( )平方米=（ ）平方米 3 米 75 厘米=（ ）米=( )米 19、把 3 吨煤平均分成 8 份，每份的质量用分数表示是（ ）吨，用小数表示 是（ ）吨，用整数表示是（ ）千克。 20、把 2 千克水果平均分成 5 份，每份是（ ）千克，每份是 2 千克的（ ）， 是 1 千克的（ ）。 21、分母是 9 的最大真分数是（ ）最小假分数是（ ）最小带分数是（ ）。 22、把 3/4、0.875、4/7、4/5 按从小大到大的顺序排列是（ ）。 二、判断。 1、分数单位是 1/10 的假分数有 9 个。 （ ） 2、3/4 是把 1 分成 4 份，表示其中的 3 分。 3、一个分数的分母，就是这个分数的分数单位。 （ ） 4、分子比分母大的分数都是假分数。 （ ） 5、在 x/6 中，当 6 是 x 的约数时，这样的假分数能化成整数。 （ ） 6、1 吨煤的 2/3 和 2 吨棉花的 1/3 同样重。 （ ） 7、分数单位越大，分数就越大。 （ ） 8、甲的 1/3 等于乙的 1/4，等于丙的 1/5，那么三个数中甲最大。（ ） 9、513 的商比 713 的商小。 （ ） 10、对于 a/b，a 和 b 中只要有一个是 0，这个分数就没有意义。 （ ） 三、选择。 1、把 3 米长的绳子对折两次，每一段是（ ）米 A、3/4 B、3/2 C、4/3 2、7 个蛋糕平均分成 8 份，每份是（ ）A、1/8 个 B、1/7 个 C、7/8 个 3、1 米的 3/7 和 3 米的 1/7 相比，（ ） A、1 米的 3/7 长 B、3 米的 1/7 长 C、一样长 4、把 10 克盐放入 100 克水中，盐占盐水的（ ） A、10/100 B、110/100 C、100/110 D、10/110 5、两个分数，分数单位大的分数，它的值（ ） A、一定大 B、一定小 C、大小不定 6、把 8 米长的电线平均分成 5 段，每段长是这段电线的（ ） A、1/5 B、1/8 C、5/83 7、下面个分数中与单位“1”最接近的数是（ ） A、2/3 B、8/9 C、1/2 D、89/90 8、如果 x/9 是真分数，x/8 是假分数，那么 x 等于（ ）A、8 B、9 C、8 和 9 9、假分数与带分数相比（ ） A、假分数大 B、带分数大 C、一样大 D、无法比较 10、下列个各组数中，都比 5/8 大的是（ ） A、7/8 和 5/7 B、5/9 和 6/8 C、7/8 和 5/9 D、1 和 1/2 四、精确计算。 1、把下面分数小数互化。m 0.72 1.8 20.6 90.7 0.625 5/9 11/4 7/20 7/9 16/5 2、用分数表示下面各题的商，结果是假分数的化成带分数或整数。 165= 5117= 165= 818= 9730= 3、写出下列带分数并化成数化成假分数。 八又四分之三 一又二十六分之十五 四又九分之七 六又七分之三 4、把下列每组中的数化成分母相同的假分数。 2 3 1 4 和 1 3 和 8 12 和 6 7 5 4 五、解决问题。 1、 把一根 20 厘米长的纸条剪成 4 次，要求剪的每小段一样长，那么每小段长 多少厘米？每小段是全长的几分之几？ 2、 王大妈用 15 米长的篱笆围成一个正方形的鸡舍，这个鸡舍的边长最长是多 少米？新课 标第 一网 3、 小明有 5 元钱，小刚有 6 元钱，小军有 8 元钱。他们平均每人有多少元？ 4、 小强家住 6 楼，现在小强已经爬到 3 楼，他已经爬了总高度的几分之几？ 5、 一块地有 3/4 公顷，已经耕了其中的 1/4，还剩几分之几没有耕？ 6、 100 千克黄豆可榨油 34 千克，平均每千克黄豆榨油多少千克？榨 1 千克油 需要多少千克黄豆？ 7、 一辆汽车行驶 180 千米需汽油 12 升？行 1 千米需要多少升汽油？ 一个公园共植树 40 棵，其中有 3 棵死亡，成活棵树占总棵树的几分之几？ 8、一个公园共植树 40 棵，其中有 3 棵死亡，则成活棵数占总棵树的几分之几？ 死亡棵树占成活棵树的几分之几 9、把一根木棒锯成 3 段需要 7 分钟，平均锯一次需要多少分钟? 10、分母是 9 的真分数、假分数、带分数各一个，它们的大小只相差两个分数单 位，这三个分数个是多少？