五年级奥数教案：第10周 数 阵 11页

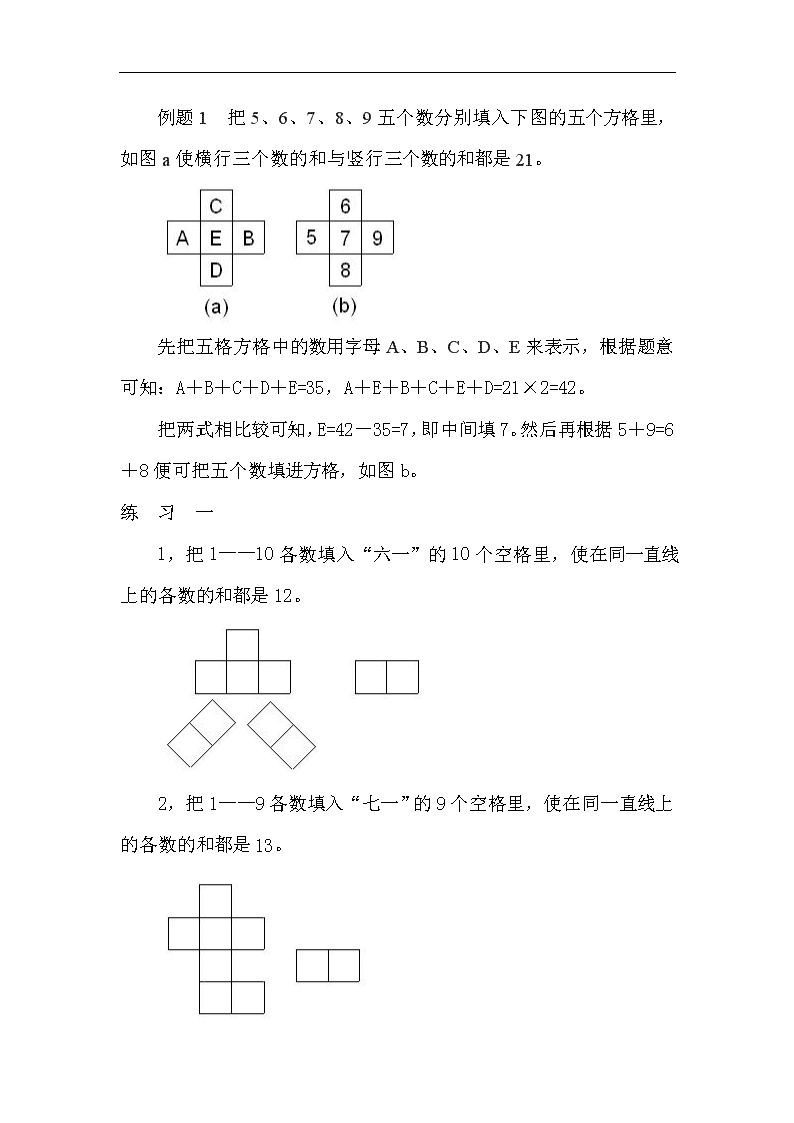
第10周 数 阵 专题简析：‎ 填“幻方”是同学们比较熟悉的一种数学游戏，由幻方演变出来的数阵问题，也是一类比较常见的填数问题。这里，和同学们讨论一些数阵的填法。‎ 解答数阵问题通常用两种方法：一是待定数法，二是试验法。‎ 待定数法就是先用字母（或符号）表示满足条件的数，通过分析、计算来确定这些字母（或符号）应具备的条件，为解答数阵问题提供方向。‎ 试验法就是根据题中所给条件选准突破口，确定填数的可能范围。把分析推理和试验法结合起来，再由填数的可能情况，确定应填的数。‎ ‎ 例题1 把5、6、7、8、9五个数分别填入下图的五个方格里，如图a使横行三个数的和与竖行三个数的和都是21。‎ 先把五格方格中的数用字母A、B、C、D、E来表示，根据题意可知：A＋B＋C＋D＋E=35，A＋E＋B＋C＋E＋D=21×2=42。‎ 把两式相比较可知，E=42－35=7，即中间填7。然后再根据5＋9=6＋8便可把五个数填进方格，如图b。‎ 练 习 一 ‎ 1，把1——10各数填入“六一”的10个空格里，使在同一直线上的各数的和都是12。‎ ‎2，把1——9各数填入“七一”的9个空格里，使在同一直线上的各数的和都是13。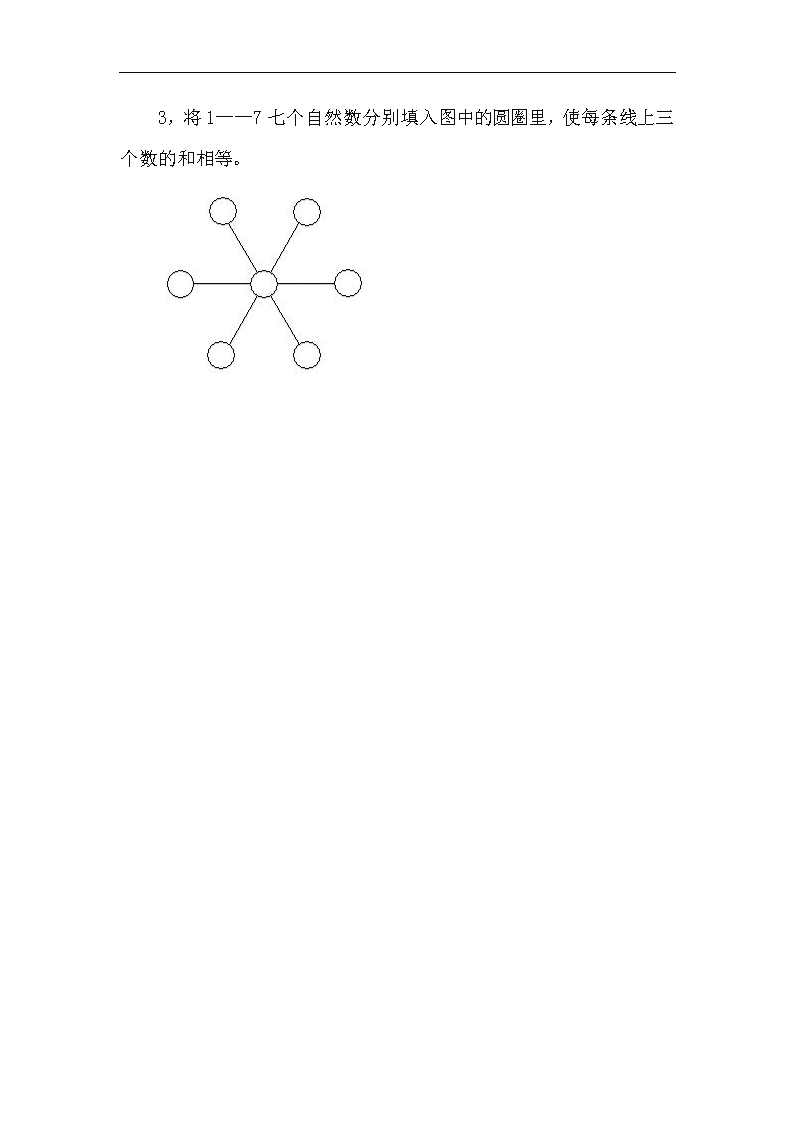‎ ‎3，将1——7七个自然数分别填入图中的圆圈里，使每条线上三个数的和相等。‎ ‎ 例题2 将1——10这十个数填入下图小圆中，使每个大圆上六个数的和是30。‎ 分析 设中间两个圆中的数为a、b，则两个大圆的总和是1＋2＋3＋……＋10＋a＋b=30×2，即55＋a＋b=60，a＋b=5。在1——10这十个数中1＋4=5，2＋3=5。‎ 当a和b是1和4时，每个大圆上另外四个数分别是（2，6，8，9）和（3，5，7，10）；当a和b是2和3时，每个大圆上另外四个数分别为（1，5，9，10）和（4，6，7，8）。‎ 练习二 ‎ 1，把1——8八个数分别填入下图的○内，使每个大圆上五个○内数的和相等。‎ ‎2，把1——10这十个数分别填入下图的○内，使每个四边形顶点的○内四个数的和都相等，且和最大。‎ ‎3，将1——8八个数填入下图方格里，使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。‎ 例题3 将1——6这六个数分别填入下图的圆中，使每条直线上三个圆内数的和相等、且最大。‎ 分析 设中间三个圆内的数是a、b、c。因为计算三条线上的和时，a、b、c都被计算了两次，根据题意可知：1＋2＋3＋4＋5＋6＋（a＋b＋c）除以3没有余数。1＋2＋3＋4＋5＋6=21，21÷3=7没有余数，那么a＋b＋c的和除以3也应该没有余数。在1——6六个数中，只有4＋5＋6的和最大，且除以3没有余数，因此a、b、c分别为4、5、6。（1＋2＋3＋4＋5＋6＋4＋5＋6）÷3=12，所以有下面的填法：‎ 练习三 ‎1，将1——6六个数分别填入下图的○内，使每边上的三个○内数的和相等。‎ ‎2，将1——9九个数分别填入下图○内，使每边上四个○内数的和都是17。‎ ‎3，将1——8八个数分别填入下图的○内，使每条安上三个数的和相等。‎ 例题4 将1——7分别填入下图的7个○内，使每条线段上三个○内数的和相等。‎ ‎ ‎ 分析 首先要确定中心圆内的数，设中心○内的数是a，那么，三条线段上的总和是1＋2＋3＋4＋5＋6＋7＋2a=28＋2a，由于三条线段上的和相等，所以（28＋2a）除以3应该没有余数。由于28÷3=9……1，那么2a除以3应该余2，因此，a可以为1、4或7。当a=1时，（28＋2×1）÷3－1=9，即每条线段上其他两数的和是9，因此，有这样的填法。‎ 练 习 四 ‎1，将1——9填入下图的○中，使横、竖行五个数相加的和都等于25。‎ ‎2，将1——11这十一个数分别填进下图的○里，使每条线上3个○内的数的和相等。‎ ‎3，将1——8这八个数分别填入下图○内，使外圆四个数的和，内圆四个数的和以及横行、竖行上四个数的和都等于18。‎ 例题5 如下图(a)四个小三角形的顶点处有六个圆圈。如果在这些圆圈中分别填上六个质数，它们的和是20，而且每个小三角形三个顶点上的数的和相等。问这六个质数的积是多少？‎ 分析 设每个小三角形三个顶点处○内数的和为X。因为中间的小三角形顶点处的数在求和时都用了三次，所以，四个小三角形顶点处数的总和是4X=20＋2X，解方程得X=10。由此可知，每个小三角形顶点处的三个质数的和是10，这三个质数只能是2、3、5。因此这6个质数的积是2×2×3×3×5×5=900。如图（b）。‎ 练习五 ‎1，将九个不同的自然数填入下面方格中，使每行、每列、每条对角线上三个数的积都相等。‎ ‎2，将1——9九个自然数分别填入下图的九个小三角形中，使靠近大三角形每条边上五个数的和相等，并且尽可能大。这五个数之和最大是多少？‎ ‎3，将1——9九个数分别填入下图○内，使外三角形边上○内数之和等于里面三角形边上○内数之和。‎