小学数学精讲教案4_2_4 图形的分割 学生版 5页

‎4-2-4.图形的分割 知识点拨 几何面积问题除了利用常规的五大模型、各种公式求得之外，还可以用图形分割的思想来做。我们发现，在迎春杯几何问题中，这类题目很多。掌握好这种思想方法，可以帮助我们解决很多几何难题。‎ 解题关键：分割其实就是运用特殊的三角形（等角直角三角形、等边三角形等）、正方形、等边图形的特殊性质进行分割而得，所以分割的关键是利用了特殊图形的关系解题。‎ 解题思想：这其实就是一种化整为零的思想，各位同学不仅要学会几何题中的这种方法，更要细细体味这种思想在解决各种问题中的妙用。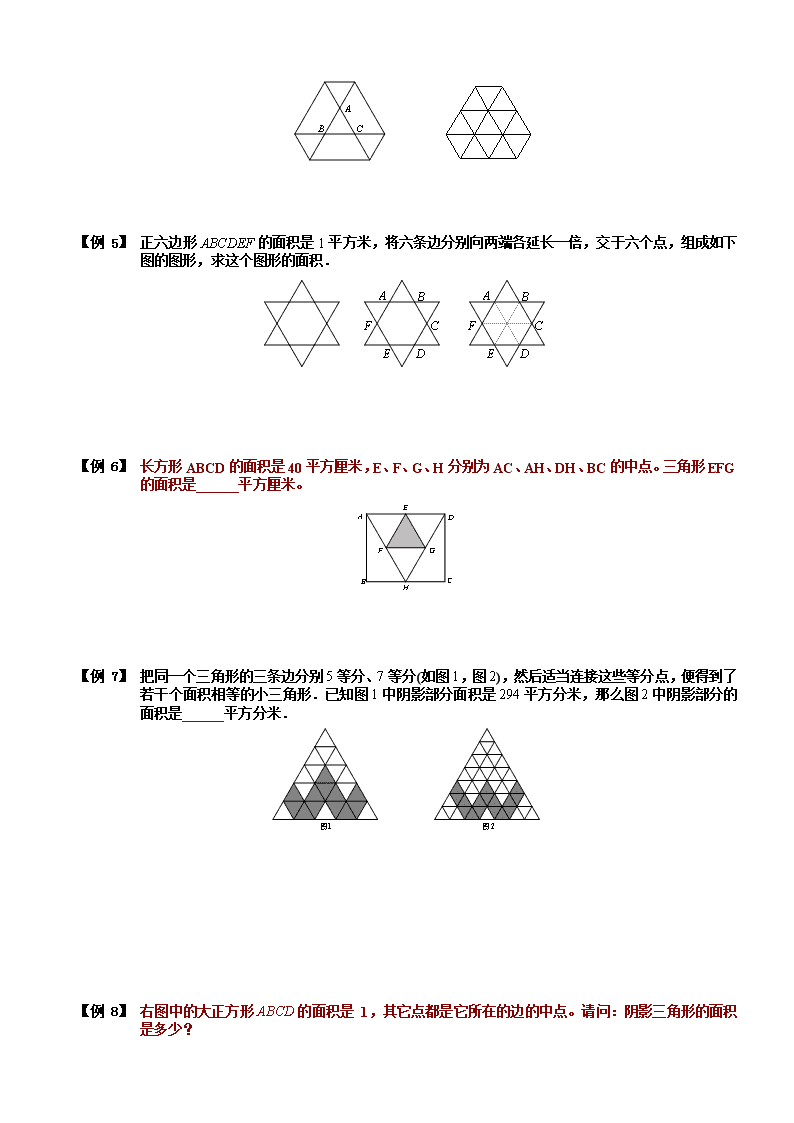‎ 例题精讲 模块一、简单分割 【例 1】 ‎3个相同的正方形纸片按相同的方向叠放在一起(如图)，顶点A和B分别与正方形中心点重合，如果所构成图形的周长是‎48厘米，那么这个图形覆盖的面积是__________平方厘米.‎ ‎ ‎ 【例 2】 正方形的面积是‎1平方米，将四条边分别向两端各延长一倍，连结八个端点得到一个正方形(如图)，求大正方形的面积．‎ 【例 3】 将边长为的正方形各边的中点连结成第二个正方形，再将第二个正方形各边的中点连结成第三个正方形，依此规律，继续下去，得到下图那么，边长为的正方形面积是图中阴影部分面积的________ 倍.‎ 【例 4】 正三角形的面积是‎1平方米，将三条边分别向两端各延长一倍，连结六个端点得到一个六边形(如右图)，求六边形的面积．‎ ‎ ‎ 【例 1】 正六边形的面积是‎1平方米，将六条边分别向两端各延长一倍，交于六个点，组成如下图的图形，求这个图形的面积．‎ 【例 2】 长方形ABCD的面积是40平方厘米，E、F、G、H分别为AC、AH、DH、BC的中点。三角形EFG的面积是 平方厘米。‎ 【例 3】 把同一个三角形的三条边分别5等分、7等分(如图1，图2)，然后适当连接这些等分点，便得到了若干个面积相等的小三角形．已知图1中阴影部分面积是294平方分米，那么图2中阴影部分的面积是______平方分米．‎ ‎ ‎ 【例 4】 右图中的大正方形ABCD的面积是 1，其它点都是它所在的边的中点。请问：阴影三角形的面积是多少？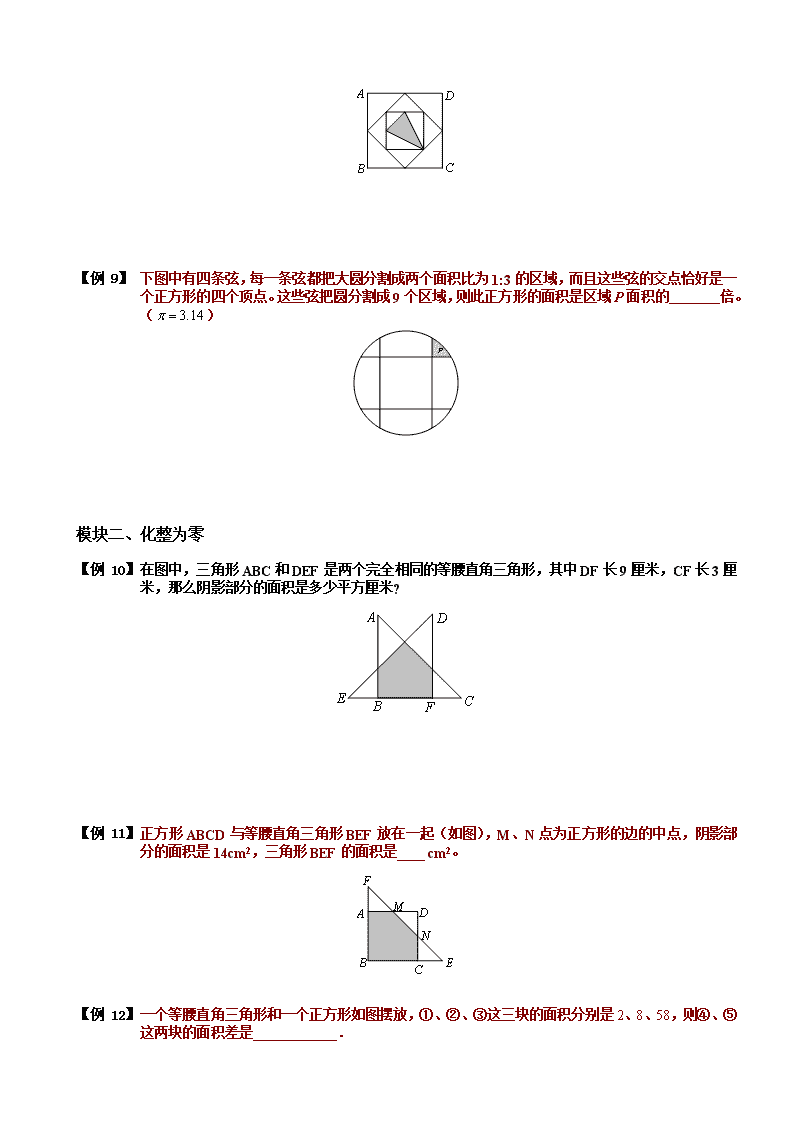‎ 【例 1】 下图中有四条弦，每一条弦都把大圆分割成两个面积比为1:3的区域，而且这些弦的交点恰好是一个正方形的四个顶点。这些弦把圆分割成9个区域，则此正方形的面积是区域P面积的 倍。（）‎ 模块二、化整为零 【例 2】 在图中，三角形ABC和DEF是两个完全相同的等腰直角三角形，其中DF长‎9厘米，CF长‎3厘米，那么阴影部分的面积是多少平方厘米?‎ 【例 3】 正方形ABCD与等腰直角三角形BEF放在一起（如图），M、N点为正方形的边的中点，阴影部分的面积是‎14cm2，三角形BEF的面积是____ cm2。‎ 【例 4】 一个等腰直角三角形和一个正方形如图摆放，①、②、③这三块的面积分别是2、8、58，则④、⑤这两块的面积差是 ．‎ ‎ ‎ 【例 1】 如图4，在长方形中，、、分别是、、上的点，且使得四边形是直角梯形，，．如果梯形的面积是平方厘米，那么长方形的面积是 平方厘米．‎ 【例 2】 一个长方形和一个等腰直角三角形如图放置，图中六块的面积分别为1，1，l，l，2，3．大长方形的面积是 ．‎ 【例 3】 如右图，一个面积为2009平方厘米的长方形，被分割成了一个长方形、两个等腰直角三角形、三个梯形．已知除了阴影长方形外，其它的五块面积都相等，且B是AC的中点；那么阴影长方形的面积是 平方厘米．‎ 【例 4】 如图中正六边形的面积为24，其中A、B、C都是所在边的中点，D是BC的三等分点，阴影部分的面积是________。‎ 【例 1】 正六边形A‎1A2A3A4A5A6的面积是2009平方厘米，B1,B2,B3,B4,B5,B6分别是正六边形各边的中点；那么图中阴影六边形的面积是　　　　平方厘米．‎ 【例 2】 如右图，长方形ABCD中被嵌入了6个相同的正方形．已知AB=‎22厘米，BC=‎20厘米，那么每一个正方形的面积为 平方厘米．‎