人教版六年级上册数学第五单元圆 习题课件 90页

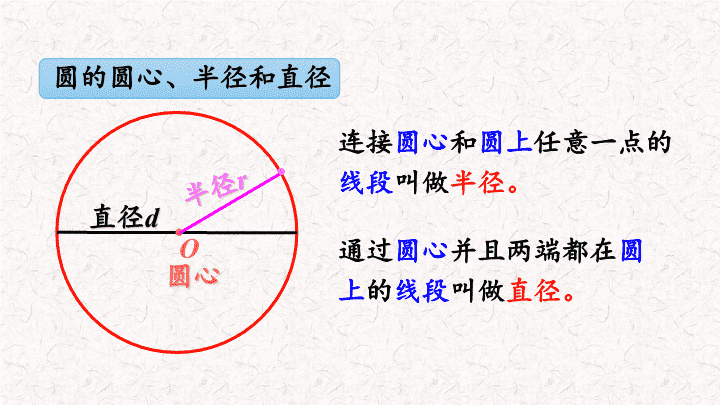
练习十三 圆 5 一、定长 二、定点 三、一只脚旋转一周 2 厘米 用 圆 规 画 圆 圆的圆心、半径和直径 连接 圆心 和 圆上 任意一点的 线段 叫做 半径。 通过 圆心 并且两端都在 圆上 的 线段 叫做 直径。 · O 圆心 半径 r 直径 d · 一个圆有无数条半径，无数条直径。 同一圆内 ，所有的 半径 都相等，所有的 直径 都相等，直径的长度是半径长度的 2 倍 。 轴对称图形 1. 井盖平面轮廓采用圆形的一个原因是圆形井盖怎么放都不会掉到井里，并且能恰好盖住井口．这是应用了圆特征中（ ）。 A . 圆心角定的位置 B . 半径决定圆的大小 C . 同一圆内所有直径都相等 D . 圆是曲边图形 2. 草坪内旋转式水龙喷头的射程是5米，5米 相当于圆的（　　） A . 半径 B . 直径 C . 周长 D . 面积 选一选 C A 按下面的要求，用圆规画圆。 （ 1 ） r ＝ 3cm （ 2 ） d ＝ 5cm （ 3 ） r ＝ 3.5cm r ＝ 3cm d ＝ 5cm r ＝ 3.5cm 3㎝ d = o o 6㎝ r = 2×3=6㎝ 6÷2=3㎝ 看图填空： o 10cm d = 10㎝ r = 5㎝ r = 高 3.5㎝ d = 3.5㎝ 3.5×2=7㎝ 看图填空： o 用下面的方法测量圆的直径。 最长的线段就是圆的直径。 0 4 1 2 3 5 6 7 8 圆的直径是 4 厘米。 填表（单位： m ）。 r 0.24 1.42 2.6 d 0.86 1.04 0.48 0.43 2.84 0.52 5.2 0.24×2 ＝ 0.48 0.86÷2 ＝ 0.43 1.42×2 ＝ 2.84 1.04÷2 ＝ 0.52 2.6×2 ＝ 5.2 在下列各图形中，你能分别画出几条对称轴。 无数条 无数条 2 条 3 条 2 条 1 条 根据对称轴画出轴对称图形的另外一半。 如图，在长方形中有三个大小相等的圆，已知这个长方形的长是 18cm ，圆的直径是多少？长方形的周长是多少？ 圆的直径： 18÷3 ＝ 6 （ cm ） 长方形的周长 ：（ 18 ＋ 6 ） ×2 ＝ 48 （ cm ） 答：圆的直径是 6cm ， 长方形的周长是 48cm 。 这节课你们都学会了哪些知识？ （ 1 ）一个圆内，直径与半径的关系： d=2r 。 （ 3 ）一个圆有 无数条 对称轴。 （ 2 ） 在 同一圆内 ，圆上两点间的距离，圆的 直径最长 。 练习十四 圆 5 围成圆的曲线的长是圆的 周长 。 圆的周长指什么？ 圆的周长除以直径的商是一个固定的数。我们把它叫做 圆周率 ，用字母 π 表示。 π ＝ 3.141592653 π ≈ 3.14 …… 如果用 C 表示圆的周长，就有： C = π d 或 C= 2 π r 一个圆形喷水池的半径是 5m ，它的周长是多少米？ 2×3.14×5 ＝ 31.4 （米） 答：它的周长是 31.4 米。 小红量得一个古代建筑中的大红圆柱的周长是 3.77m 。这个圆柱的直径是多少米？（得数保留一位小数。） 3.77÷3.14 ≈ 1.2 （米） 答：这个圆柱的直径约 1.2 米。 看图填空（单位： cm ）。 （ 1 ） （ 2 ） 正方形的周长是（ ） cm ，圆的周长是（ ） cm 。 其中一个圆的周长是（ ） cm ，长方形的周长是（ ） cm 。 16 12.56 9.42 21 在一个圆形亭子里，小丽沿着直径从一端走 12 步到达另一端，每步长大约是 55cm 。这个圆的周长大约是多少米？ 3.14× （ 55×12 ）＝ 2072.4 （ cm ） 2072.4cm ＝ 20.724m ≈ 21m 答：这个圆的周长大约是 21 米。 一只挂钟的分针长 20cm ，经过 30 分钟后，分针的尖端所走的路程是多少厘米？经过 45 分钟呢？ 2×3.14×20× ＝ 62.8 （ cm ） 2×3.14×20× ＝ 94.2 （ cm ） 答：经过 30 分钟后分针的尖端所走的路程是 62.8cm 。 经过 45 分钟后分针的尖端所走的路程是 94.2cm 。 一个圆形牛栏的半径是 15m ，要用多长的粗铁丝才能把牛栏围上 3 圈？（接头处忽略不计。）如果每隔 2m 打一根木桩，大约要打多少根木桩？ 15×2×3.14×3 ＝ 282.6 （ m ） 答：要用 282.6m 长的铁丝才能把牛栏围上 3 圈。 15×2×3.14÷2 ≈ 47 （根） 答：大约要打 47 根木桩。 杂技演员表演独轮车走钢丝，车轮的直径为 40cm ，要骑过 50.24m 长的钢丝，车轮大约要转动多少周？ 3.14×40 ＝ 125.6 （ cm ） 125.6cm ＝ 1.256m 50.24÷1.256 ＝ 40 （周） 答：车轮大约要转动 40 周。 港珠澳大桥是世界最长的跨海大桥，全长近50公里、工程造价逾700亿港元，其中建设难度最大的 海底隧道全长5.6千米，是世界最长的公路沉管隧道。一种汽车的车轮外直径是50厘米，按照每分钟转1000圈计算，通过这个隧道大约需要多少分钟？（得数保留一位小数） 3.14 × 50 × 1000=157000 （厘米） =1.57 （千米） 5.6 ÷ 1.57≈3.6 （分钟） 答： 通过这个隧道大约需要 3.6 分钟。 在一个周长为 100cm 的正方形纸片内，要剪一个最大的圆，这个圆的半径是多少厘米？ 100÷4× ＝ 12.5 （厘米） 答：这个圆的半径是 12.5 厘米。 李明家一扇门上要装上形状如右图所示的装饰木条，需要木条多少米？ 50×3.14× ＝ 78.5 （ cm ） 50×4 ＝ 200 （ cm ） 200 ＋ 78.5 ＝ 278.5 （ cm ） 278.5cm ＝ 2.785m 答：需要木条 2.785m 。 把圆柱形物体分别捆成如下图（从底面方向看）的形状，如果接头处不计，每组至少需要多长的绳子？你发现了什么？ 第一幅图： 7×2 ＋ 3.14×7 ＝ 35.98 （ cm ） 第二幅图： 7×4 ＋ 3.14×7 ＝ 49.98 （ cm ） 第三幅图： 7×8 ＋ 3.14×7 ＝ 77.98 （ cm ） 这节课你们都学会了哪些知识？ 1 、围成圆的曲线的长叫做 圆的周长 。 2 、圆的周长计算公式： C=2πr 。 3 、根据实际情况灵活运用所学知识。 练习十五 圆 5 圆的直径与半径的关系： 圆的面积计算的公式： d=2r S=πr² 圆的周长计算的公式： C=2πr （ 1 ） S 环 ＝π R 2 - π r 2 （ 2 ） S 环 ＝π× ( R 2 - r 2 ) R r 圆环的面积计算公式： o S 正 - S 圆 S 圆 - S 正 S 圆外切正方形 S 圆 内 切正方形 圆外切和圆内切正方形的面积计算公式： 半径 直径 圆面积 4cm 9cm 6cm 20cm 完成下表。 8cm 3cm 4.5cm 40cm 50.24cm² 63.585cm² 28.26cm² 1256cm² 计算下面各圆的周长和面积。 d = 10 cm r = 3 cm C = 3.14×10 = 31.4 （ cm ） S = 3.14×(10÷2) 2 = 78.5 （ cm 2 ） S = 3.14×3 2 = 28.26 （ cm 2 ） C = 2×3.14×3 = 18.84 （ cm ） 公园草地上一个自动旋转喷灌装置的射程是 10m ，它能喷灌的面积是多少？ S = π r 2 = 3.14×10 2 = 3.14×100 = 314 （ m 2 ） 答：它能喷灌的面积是 314m 2 。 小刚量得一棵树干的周长是 125.6 cm 。这棵树干的横截 面近似于圆，它的面积大约是多少？ r = 125.6÷3.14÷2 = 20 （ cm ） C = 2 π r S = π r 2 = 3.14×20 2 = 3.14×400 = 1256 （ cm 2 ） 答：它的面积大约是 1256cm 2 。 具有近600年历史的北京天坛祈年殿为砖木结构，殿高38米，底层直径32米，三层重檐向上逐层收缩作伞状。殿内有28根金丝楠木大柱，里圈的4根寓意春、夏、秋、冬四季，每根高约19米，直径1.2米。因为它们是殿内最高的柱子，所以也叫通天柱，取的是和上天互通声息的意思。 （ 1 ）根据上面的信息，求出祈年殿的面积。 3.14 ×（ 32 ÷ 2 ） ²=803.84 （平方米） 答：祈年殿的面积是 803.84 平方米。 具有近600年历史的北京天坛祈年殿为砖木结构，殿高38米，底层直径32米，三层重檐向上逐层收缩作伞状。殿内有28根金丝楠木大柱，里圈的4根寓意春、夏、秋、冬四季，每根高约19米，直径1.2米。因为它们是殿内最高的柱子，所以也叫通天柱，取的是和上天互通声息的意思。 （ 2 ）通天柱的占地面积是多少平方米？ （结果保留两位小数） 3.14 ×（ 1.2 ÷ 2 ） ² × 4≈4.52 （平方米） 答：通天柱的占地面积是 4.52 平方米 。 右图是一块玉壁，外直径 18cm ， 内直径 7cm 。这块玉壁的面积是多少？ 3.14× (9 2 - 3.5 2 ) = 3.14× 68.75 = 215.875 （ cm² ） 外半径： 18÷2 内半径： 7÷2 = 9 （ cm ） = 3.5 （ cm ） 答：这块玉壁的面积是 215.875cm 2 。 = 3.14× (81 - 12.25) 图中的大圆半径等于小圆的直径，请你求出阴影部分的面积。 6 cm 小圆半径： 6÷2 = 3 （ cm ） 3.14× (6 2 - 3 2 ) = 3.14× 27 = 84.78 （ cm² ） 答：阴影部分的面积是 84.78cm 2 。 = 3.14× (36 - 9) 计算下面图形的周长。 8cm 12cm 大半圆弧 + 小半圆弧 + 2 条线段 C 大半圆弧 = π d ÷2 = 3.14×12÷2 = 18.84 （ cm ） C 小半圆弧 = π d ÷2 = 3.14×8÷2 = 12.56 （ cm ） 18.84 + 12.56 + 4 = 35.4 （ cm ） 两条线段长度： 12 - 8 = 4 （ cm ） 答：图形的周长是 35.4cm 。 . 计算下面图形的面积。 12cm 8cm 3.14× (12 2 - 8 2 ) = 3.14× 80 = 251.2 （ cm² ） 答：圆环的面积是 251.2cm 2 。 = 3.14× (144 - 64) 右图中的铜钱直径 28mm ，中间的正方形边长 为 6mm 。这个铜钱的面积是多少？ 3.14× 14 2 - 6 2 = 615.44 - 36 = 579.44 （ mm² ） 答：这个铜钱的面积是 579.44mm 2 。 = 3.14× 196 - 36 r = 28÷2 = 14 （ mm ） 一个运动场如右图，两端是半圆形，中间是长方形。这个 运动场的周长是多少米？面积是多少平方米？ 100m 32m O C = 2×3.14×32 + 100×2 = 200.96 + 200 = 400.9 （ m ） S = 3.14×32 2 + 100×(32×2) = 3.14×32 2 + 100×64 = 3215.36 + 6400 = 9615.36 （ m 2 ） 答：这个运动场的周长是 400.9m ，面积是 9615.36m 2 。 右图中的花瓣状门洞的边是由 4 个直径相等的半圆组成的。 这个门洞的周长和面积分别是多少？ = 2×3.14×1 = 6.28 （ m ） C = 2C 圆 S = 2S 圆 + S 正方形 = 2×3.14×(1÷2) 2 + 1 2 = 2×3.14×0.25 + 1 = 1.57 + 1 = 2.57 （ m 2 ） 答：这个门洞的周长是 6.28m ，面积是 2.57m 2 。 高致病性的禽流感是比非典病毒传染速度更快的传染病。为了防止禽流感的蔓延，政府规定：离疫点3千米的范围内为疫区（或捕杀区），所有的禽类全部捕杀深埋；离疫点3千米至5千米范围内为免疫区，所有的禽类强制免疫，同时对捕杀区和免疫区内的村庄，实行道路全封闭管理。 A . 请你在图中分别画出捕杀区和免疫区的范围，并求出 捕杀区和免疫区之间的面积是多少平方千米？ 3.14 ×（ 5 ² -3 ² ） =50.24 （平方千米） 捕杀区 免疫区 答： 捕杀区和免疫区之间的面积是 50.24 平方千米 。 土楼是福建、广东等地区的一种建筑形式，被列入“世界物质文化名录”，土楼的外围形状有圆形、方形、椭圆形等。有两座地面是圆环形的土楼，其中一座外直径 34 m ，内直径 14 m ；另一座外直径 26 m ，内直径也是 14 m ；两座土楼的房屋占地面积相差多少？ r 1 外 = 34÷2 r 1 内 = r 2 内 = 14÷2 r 2 外 = 26÷2 = 17 （ m ） = 7 （ m ） = 13 （ m ） 3.14× (17 2 - 7 2 )- 3.14× (13 2 - 7 2 ) = 3.14× 120 = 376.8 （ m² ） = 3.14× (17 2 - 7 2 - 13 2 + 7 2 ) = 3.14× (17 2 - 13 2 ) 答：两座土楼的房屋占地面积相差 376.8m 2 。 一个圆的周长是 62.8m ，半径增加了 2m 后，面积增加了多少？ C = 2 π r r = C ÷(2 π ) = 62.8÷(2×3.14) = 62.8÷6.28 = 10 （ m ） = π (r 增加后 2 - r 2 ) = 3.14×(144 - 100) = 3.14×44 = 138.16 （ m 2 ） 答：面积增加了 138.16m 2 。 r 增加后 = 10 + 2 = 12 （ m ） = 3.14×(12 2 - 10 2 ) S = S 增加后 - S 原来 篮球场上的 3 分线是由两条平 你根据图中的数据计算出 3 分 行线段和一个半圆组成的。 线的长度和 3 分线内区域的面 请 积。（得数保留两位小数。） 3 分线的长度 = 2×3.14×6.75÷2 + 1.575×2 = 21.195 + 3.15 = 24.345 ≈ 24.35 （ m ） 答： 3 分线的长度是 24.35m 。 S = 3.14×6.75 2 ÷2 + 1.575×(6.75×2) = 3.14×45.5625÷2 + 1.575×13.5 = 71.533125 + 21.2625 ≈ 92.80 （ m 2 ） 答： 3 分线内区域的面积是 92.80m 2 。 = 92.795625 篮球场上的 3 分线是由两条平 你根据图中的数据计算出 3 分 行线段和一个半圆组成的。 线的长度和 3 分线内区域的面 请 积。（得数保留两位小数。） 这节课你们都学会了哪些知识？ 要灵活运用 圆的面积 计算公式和 圆环的面积 计算公式解决实际问题。 练习十六 圆 5 B O 弧 图上 A 、 B 两点之间的部分叫做弧，读作“ 弧 AB ”。 A 什么是圆上的“弧” B O 半径 半径 弧 一条弧和经过这条弧两端的两条半径所围成的图形叫做 扇形 。 A 什么叫“扇形”？ A B O 圆心角 半径 半径 弧 顶点在圆心的角叫做 圆心角 。 什么是圆的“圆心角” 在同一个圆中，扇形的大小与什么有关系？ 扇形的大小与这个扇形的圆心角的大小有关。 以半圆为弧的扇形的圆心角是多少 度？以 圆为弧的扇形呢？ 以半圆为弧的扇形的圆心角是 180° 。 360× ＝ 90( 度 ) 以半圆为弧的扇形的圆心角是多少 度？以 圆为弧的扇形呢？ 我是小法官。（对的打“√”错的打“ × ”。） 1. 圆的一部分就是扇形。 （ ） 2. 扇形和圆一样，也是轴对称图形，但扇形只有一条对称轴。 （ ） 3. 在一个圆内，最多能画出 360 个相等的扇形。（ ） × √ × 指出下列物体中的扇形。 答案不唯一，合理即可。 下面图形中哪些角是圆心角？在（ ）里画“√”。 （ ） （ ） （ ） （ ） √ √ O O A B B A O B A O A B 画一个半径是 2cm 的圆，再在圆中画一个圆心角是 100 ° 的扇形。 O r = 2cm 100 ° 如图，四个圆的半径都为3厘米，圆心分别在四边形的四个顶点上，则阴影部分的面积是多少平方厘米？ 举手回答：阴影部分能否组成一个圆形？请说明理由！ 3.14 × 3²=28.26 （平方厘米） 答： 阴影部分的面积是 28.26 平方厘米。 你在生活中见过下面这些图案吗？ 像下面这样一个圆环被截得的部分叫做扇环。你能求出下面 扇环的面积吗？ r = 5 dm 2 dm O r = 4 dm 1 dm O S 扇环 = S 大扇形 - S 小扇形 r 小扇形 = 5-2 = 3 （ dm ） = 3.14×5 2 ÷4 - 3.14×3 2 ÷4 = 3.14×25÷4 - 3.14×9÷4 = 19.625 - 7.065 = 12.56 （ dm 2 ） r = 5 dm 2 dm O r 小扇形 = 4-1 = 3 （ dm ） S 扇环 = S 大扇形 - S 小扇形 = 3.14×4 2 ÷2 - 3.14×3 2 ÷2 = 3.14×16÷2 - 3.14×9÷2 = 25.12 - 14.13 = 10.99 （ dm 2 ） 拼在一起相于一个半圆环。 r = 4 dm 1 dm O 这节课你们都学会了哪些知识？ 1 、 一条弧和经过这条弧两端的两条半径所围成的图形叫做 扇形 。 2 、 顶点在圆心的角叫做 圆心角 。 3 、 在同一个圆中，圆心角越大，扇形越大。 练习十七 圆 5 本单元学习了哪些有关圆的知识？ 圆的认识 圆心 半径 直径 圆的周长 圆的面积 圆环的面积 圆 组合图形的面积 扇形 外圆内方 外方内圆 圆的认识 圆是由一条曲线围成的封闭图形。它是平面图形。 圆心确定圆的位置。 o r d d =2 r r = d ÷2 半径（或直径）决定圆的大小。 有无数条对称轴。 圆的 周长、面积 圆的周长的计算公式： C ＝ π d 或 C ＝ 2 π r 。 πr × r S = πr 2 圆的面积 = 在大圆中间挖去一个小圆，剩下的部分就形成了一个圆环，组成圆环的是两个 同心圆 。 S 环 = πR 2 － π r 2 S 环 = π ( R 2 － r 2 ) 圆 环 的 面积 组合图形 的 面积 o . S 阴 = S 正 － S 圆 o S 阴 = S 圆 － 2 S 三角形 扇 形 A B O 半径 半径 弧 一条弧和经过这条弧两端的两条半径所围成的图形叫做 扇形 。 图上 A 、 B 两点之间的部分叫做弧，读作“弧 AB ”。 扇 形 0 顶点在圆心的角叫做 圆心角 。 在同一个圆中， 扇形的大小 与这个扇形的 圆心角的大小 有关。 下图中的双面绣作品中间部分的画是一个直径是 20 cm 的圆。这幅画的面积是多少？ 3.14× （ 20÷2 ） ² ＝ 314 （ cm ² ） 答：这幅画的面积是 314 cm ² 。 儿童乐园要修建一个圆形旋转木马场地，木马旋转范围的 直径是 8 m ，周边还要留出 1m 宽的小路 ，并在外侧围上栏杆，这块场地的 占地面积 是多少？ 3.14× （ 8÷2 ＋ 1 ） ² ＝ 78.5 （ m ² ） 答：这块场地的占地面积是 78.5 m ² 。 你能根据提意画出示意图吗？ 8m 1m 一个羊圈依墙而建，呈半圆形，半径是 5 m 。 （ 1 ）修这个羊圈需要多长的栅栏？ 2×3.14×5÷2 ＝ 15.7 （ m ） 答：修这个羊圈需要 15.7 m 的栅栏。 一个羊圈依墙而建，呈半圆形，半径是 5 m 。 （ 2 ）如果要扩建这个羊圈，把它的直径 增加 2 m 。羊圈的面积增加了多少？ 3.14×[ （ 5 ＋ 2÷2 ） ² － 5²]÷2 ＝ 17.27 （ m ² ） 答：羊圈的面积增加了 17.27 m ² 。 5m 1m 判断对错，对的画“ √ ”，错的画“ × ”。 （ 1 ）圆周率 π 就是 3.14 。（ ） （ 2 ）圆的半径扩大到原来的 2 倍，周长和面积也扩大到原来的 2 倍。（ ） （ 3 ）半径相等的两个圆周长相等。（ ） （ 4 ）两个圆的直径相等，它们的半径也一定相等。 （ ） （ 5 ）用 4 个圆心角都是 90 ° 的扇形，一定可以拼成一个圆 。（ ） × × √ √ × 如下图，一台压路机的 前轮直径 是 1.7 m ，如果前轮每分钟转动 6 周 ，压路机 10 分钟 前进多远？ 3.14×1.7×6×10 ＝ 320.28 （ m ） 答：压路机 10 分钟前进 320.28 m 。 想一想：实际上求的是什么？与圆的什么有关系？ 如下图，街心公园有两块 半圆形 的草坪，它们的 周长 都是 128.5 m ，这两块草坪的 总面积 是多少？ 一块半圆形草坪的周长等于整个 圆周长的一半 与 2 条半径 的长度之 和 ，即 π r ＋ 2 r ＝ 128.5 m 。 先根据一块半圆形草坪的 周长 求出圆的 半径 ，再利用圆的面积公式求出这两块草坪的 总面积 ，即一个 整圆的面积 。 128.5÷ （ 3.14 ＋ 2 ）＝ 25 （ m ） 3.14×25² ＝ 1962.5 （ m ² ） 答：这两块草坪的总面积是 1962.5 平方米。 如下图，街心公园有两块 半圆形 的草坪，它们的 周长 都是 128.5 m ，这两块草坪的 总面积 是多少？ 如下图，中间是 边长为 1 cm 的正方形，与这个正方形每一条边相连的都是 圆心角为 90 ° 的扇形，整个图形的 面积 是多少 ？ 1² ＋ 3.14×1² ＝ 4.14 （ cm ² ） 答：整个图形的面积是 4. 14 cm ² 。 如图，学校操场的跑道由 正方形的两条对边 和 两个半圆 组成。小晨在操场上跑了 5 圈 ，一共是多少米？ （ 3.14×50 ＋ 50×2 ） ×5 ＝ 1285 （ m ） 答：一共是 1285 米 。 50 m 操场跑道的长度等于一个 整圆的周长 与 两条 直的跑道 的长度之 和 。 如图所示，一块边长为8m的正方形草地，在图中相对的顶点处各拴有一只羊，拴羊的绳长都是8m．两只羊都能吃到草的草地面积（阴影部分）是多少平方米？ 3.14 × 8² ÷ 2 -8²=36.48 （平方米） 答： 两只羊都能吃到草的草地面积（阴影部分）是 36.48 平方 米 。 这节课你们都学会了哪些知识？ 1. 通过圆的周长和面积公式的推导，我学到了 化曲为直 的方法。 2. 圆在生活中的应用太多了，学会圆的知识可以 解决 许多 实际问题 。