六年级数学下册第5章数学广角鸽巢问题（2）课件新人教版 16页

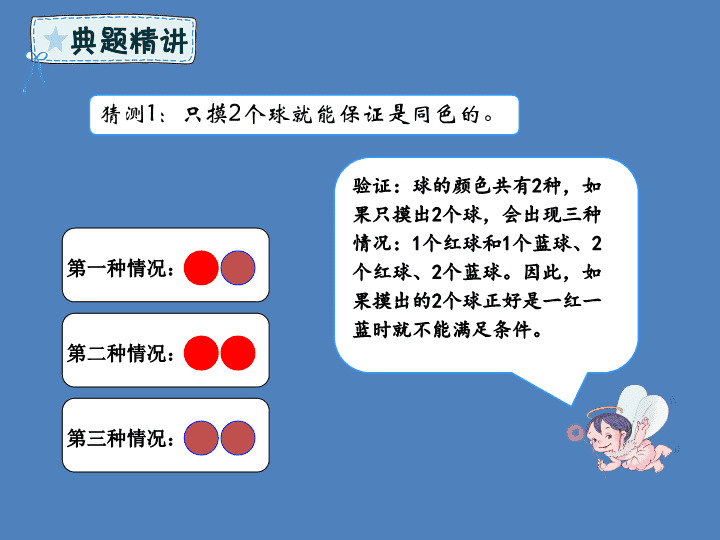
鸽巢问题（ 2 ） 5 数学广角 摸出 5 个球，肯定有 2 个同色的，因为 …… 盒子里有同样大小的红球和蓝球各 4 个，要想摸出的球一定有 2 个同色的，至少要摸出几个球？ 只摸 2 个球能保证是同色的吗？ 有两种颜色。那摸 3 个球就能保证 …… 第一种情况： 第二种情况： 第三种情况： 验证：球的颜色共有 2 种，如果只摸出 2 个球，会出现三种情况： 1 个红球和 1 个蓝球、 2 个红球、 2 个蓝球。因此，如果摸出的 2 个球正好是一红一蓝时就不能满足条件。 猜测 1 ：只摸 2 个球就能保证是同色的。 猜测 2 ：摸出 5 个球，肯定有 2 个是同色的。 第一种情况： 第二种情况： 第三种情况： 第四种情况： 验证：把红、蓝两种颜色看成 2 个“鸽巢”，因为 5 ÷ 2 ＝ 2 …… 1 ，所以摸出 5 个球时，至少有 3 个球是同色的，显然，摸出 5 个球不是最少的。 第一种情况： 第二种情况： 猜测 3 ：有两种颜色。那摸 3 个球就能保证有 2 个同色的球。 盒子里有同样大小的红球和蓝球各 4 个，要想摸出的球一定有 2 个同色的，至少要摸出几个球？ 只要摸出的球数比它们的颜色种数 多 1 ，就能 保证 有两个球同色。 1 ． 10 个孩子分进 4 个班 , 则至少有一个班分到的人数不少于 ( ) 个。 A ． 1 B ． 2 C ． 3 D ． 4 C 10 个孩子分进 4 个班，这里把班级个数看作“抽屉”，把孩子的个数看作“物体个数”， 10÷4=2 （个） …2 人，所以至少有一个班分到的人数不少于 2+1=3 （人）。 2 ．王东玩掷骰子游戏，要保证掷出的骰子总数至少有两次相同，他最少应掷（ ）次。 A ． 5 B ． 6 C ． 7 　 D ．８ C 骰子能掷出的结果只有 6 种，掷 7 次的话必有 2 次相同；即把骰子的出现的六种情况看作“抽屉”，把掷出的次数看作“物体的个数”，要保证至少有两次相同，那么物体个数应比抽屉数至少多 1 。 向东小学六年级共有 367 名学生，其中六（ 2 ）班有 49 名学生。 他们说得对吗？为什么？ 367÷365 ＝ 1……2 1 ＋ 1 ＝ 2 49÷12 ＝ 4……1 4 ＋ 1 ＝ 5 六年级里至少有两人的生日是同一天。 六（ 2 ）班中至少有 5 人是同一个月出生的。 2. 把红、黄、蓝、白四种颜色的球各 10 个放到一个袋子里。至少取多少个球，可以保证取到两个颜色相同的球？ 我们从 最不利的原则 去考虑： 假设我们每种颜色的都拿一个，需要拿 4 个，但是没有同色的，要想有同色的需要再拿 1 个球，不论是哪一种颜色的，都一定有 2 个同色的。 4 ＋ 1 ＝ 5 3. 希望小学篮球兴趣小组的同学中，最大的 12 岁，最小的 6 岁，最少从中挑选几名学生，就一定能找到两个学生年龄相同。 7 ＋ 1 ＝ 8 从 6 岁到 12 岁有几个年龄段？ 4. 从一副扑克牌（ 52 张，没有大小王）中要抽出几张牌来，才能保证有一张是红桃？ 54 张呢？ 13×3 ＋ 1 ＝ 40 最后为什么要加 1 ？ 2＋ 13×3 ＋ 1 ＝ 42 13 13 13 13 德国 数学家 狄里克雷 （ 1805.2.13. ～ 1859.5.5. ） 抽屉原理是组合数学中的一个重要原理，它最早由德国数学家狄里克雷（ Dirichlet ）提出并运用于解决数论中的问题，所以该原理又称“狄里克雷原理”。抽屉原理有两个经典案例，一个是把 10 个苹果放进 9 个抽屉里，总有一个抽屉里至少放了 2 个苹果，所以这个原理又称“抽屉原理”；另一个是 6 只鸽子飞进 5 个鸽巢，总有一个鸽巢至少飞进 2 只鸽子，所以也称为“鸽巢原理”。 这节课你有什么收获？ 物体数 ÷ 抽屉数＝商 …… 余数 至少数： 商＋ 1 从 最不利的原则 去考虑 作业 请完成教材第71页练习十三第 3 题、第 4 题。 xx 小学 x 年级 x 班 xxx