人教版 初中数学中考一轮复习---勾股定理及其逆定理（含解析） 11页

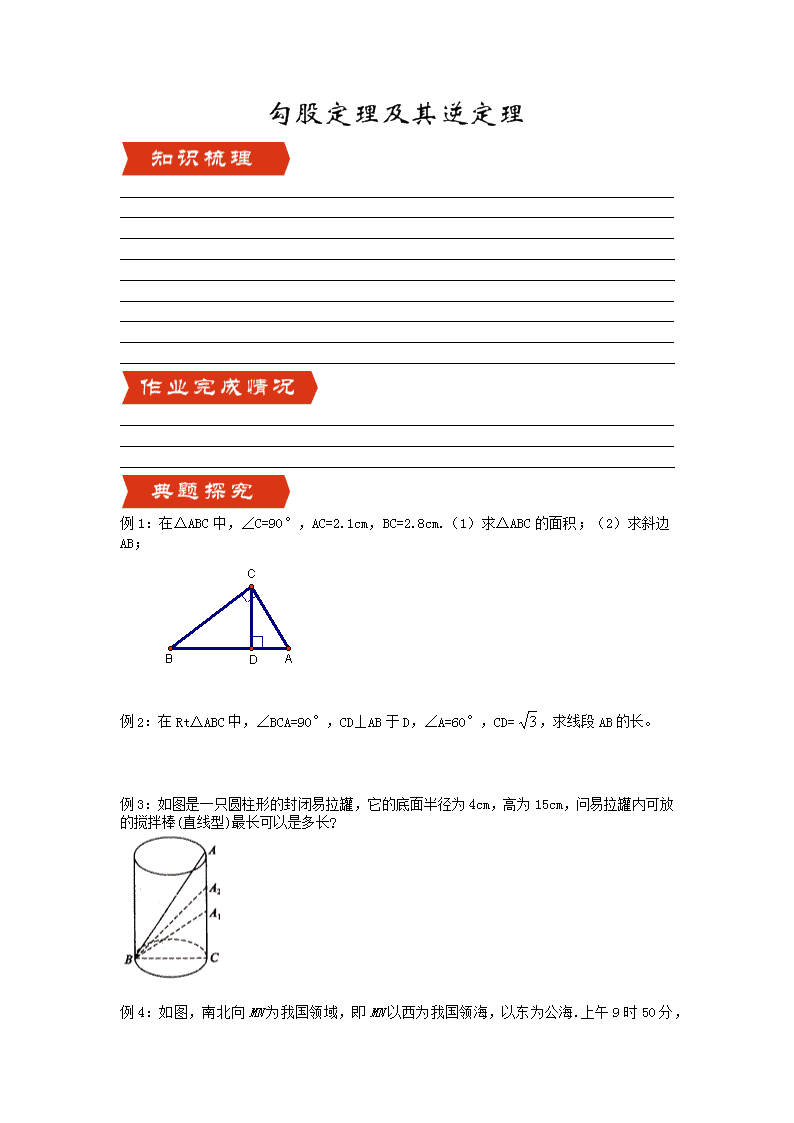
勾股定理及其逆定理 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例1：在△ABC中，∠C=90°，AC=2.1cm，BC=2.8cm.（1）求△ABC的面积；（2）求斜边AB；‎ 例2：在Rt△ABC中，∠BCA=90°，CD⊥AB于D，∠A=60°，CD=，求线段AB的长。‎ 例3： 如图是一只圆柱形的封闭易拉罐，它的底面半径为4cm，高为15cm，问易拉罐内可放的搅拌棒(直线型)最长可以是多长?‎ 例4：如图，南北向MN为我国领域，即MN 以西为我国领海，以东为公海.上午9时50分，我反走私A艇发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海开来，便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C两艇的距离是13海里，A、B两艇的距离是5海里；反走私艇测得离C艇的距离是12海里.若走私艇C的速度不变，最早会在什么时间进入我国领海？‎ A组 ‎1．已知两条线段的长为5cm和12cm,当第三条线段的长为           cm时,这三条线段能组成一个直角三角形.‎ B组 ‎2．下列各组数中，以a，b，c为边的三角形不是Rt△的是（　　）‎ ‎ A、a=1.5，b=2,c=3 B、a=7,b=24,c=25‎ C、a=6,b=8,c=10 D、a=3,b=4, c=5‎ ‎3、已知△ABC的两边AB、AC的长是方程的两个实数根，第三边BC＝5。‎ ‎（1）为何值时，△ABC是以BC为斜边的直角三角形；‎ ‎（2）为何值时，△ABC是等腰三角形，求出此时其中一个三角形的面积。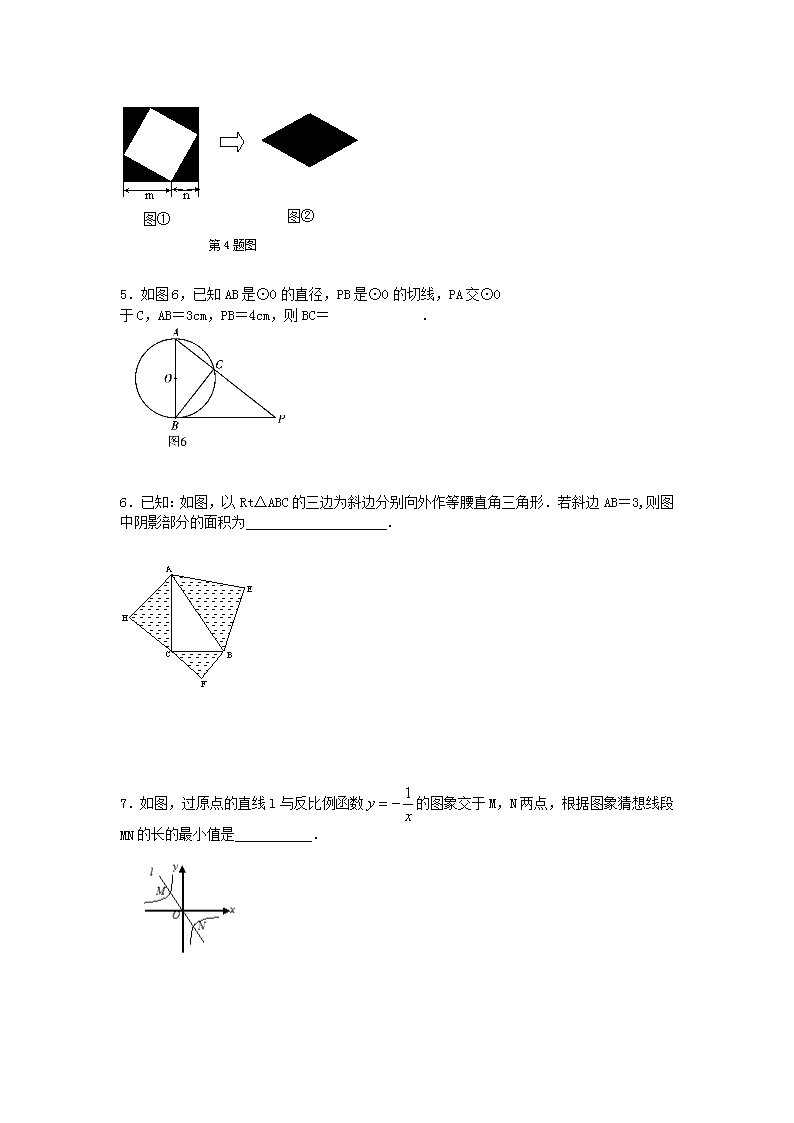‎ ‎ ‎ ‎4.图①是一个边长为的正方形，小颖将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式子是（ ）‎ A． ‎ B． ‎ C． ‎ D．‎ 图①‎ 图②‎ 第4题图 ‎ ‎ ‎5．如图6，已知AB是⊙O的直径，PB是⊙O的切线，PA交⊙O 于C，AB＝3cm，PB＝4cm，则BC＝ ． ‎ ‎ ‎6．已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB＝3,则图中阴影部分的面积为          ．‎ ‎ ‎ ‎7．如图，过原点的直线l与反比例函数的图象交于M，N两点，根据图象猜想线段MN的长的最小值是___________．‎ ‎8．长为4m的梯子搭在墙上与地面成45°角，作业时调整为60°角（如图所示），则梯子的顶端沿墙面升高了           m．‎ ‎ ‎ ‎9．如图，长方体的底面边长分别为1cm 和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要           cm；如果从点A开始经过4个侧面缠绕圈到达点B，那么所用细线最短需要           cm． ‎ B A ‎6cm ‎3cm ‎1cm ‎10、如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），（0，1），点D是线段BC上的动点（与端点B、C不重合），过点D作直线＝－＋交折线OAB于点E．‎ ‎（1）记△ODE的面积为S，求S与的函数关系式；‎ ‎（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形OA1B1C1，试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由.‎ C D B A E O B组 ‎1. 以下四个命题正确的是（　　）‎ ‎　‎ A．‎ 任意三点可以确定一个圆 ‎　‎ B．‎ 菱形对角线相等 ‎　‎ C．‎ 直角三角形斜边上的中线等于斜边的一半 ‎　‎ D．‎ 平行四边形的四条边相等 ‎2. 如图，⊙O的半径为3，P是CB延长线上一点，PO=5，PA切⊙O于A点，则PA=　　．‎ ‎3. 如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（　　）‎ ‎　‎ A．‎ ‎1，2，3‎ B．‎ ‎1，1，‎ C．‎ ‎1，1，‎ D．‎ ‎1，2，‎ ‎4. 如图，已知∠AOB=60°，点P在边OA上，OP=12，点M，N在边OB上，PM=PN，若MN=2，则OM=（　　）‎ ‎　‎ A．‎ ‎3‎ B．‎ ‎4‎ C．‎ ‎5‎ D．‎ ‎6‎ ‎5. 如图，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上，若AM：MB=AN：ND=1：2，则tan∠MCN=（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎﹣2‎ ‎6. 如图1，有一个“顽皮虫”想从点A沿棱长为1cm的正方体的表面爬到点B，求它所爬过的最短路程．‎ ‎7. 在△ABC中，AB=13cm，BC=10cm，BC边上的中线AD=12cm，求AC ‎8. 已知：如图，等边△ABC的边长是6cm。‎ ‎⑴求等边△ABC的高。 ⑵求S△ABC。‎ ‎9. 判断由线段a、b、c组成的三角形是不是直角三角形 ‎（1）a=15，b=8，c=17；（2）a=13，b=14，c=15‎ ‎10. 勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：‎ 将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 勾股定理及其逆定理 例1：在△ABC中，∠C=90°，AC=2.1cm，BC=2.8cm.（1）求△ABC的面积；（2）求斜边AB；‎ 解：（1）S△ABC=‎ ‎ （2）‎ 例2：在Rt△ABC中，∠BCA=90°，CD⊥AB于D，∠A=60°，CD=，求线段AB的长。‎ 分析：勾股定理的使用范围是在直角三角形中，因此注意要创造直角三角形，作高是常用的创造直角三角形的辅助线做法。欲求高CD，可将其置身于Rt△ADC或Rt△BDC中，但只有一边已知，根据等腰三角形三线合一性质，可求AD=CD=AB=3cm，则此题可解。‎ 例3： 如图是一只圆柱形的封闭易拉罐，它的底面半径为4cm，高为15cm，问易拉罐内可放的搅拌棒(直线型)最长可以是多长?‎ 解答 如图，当搅拌棒在AB位置时最长，过B画底面直径BC，则在Rt△ABC中，AC＝15cm， BC＝4×2＝8cm 根据勾股定理得 所以可放的最长搅拌棒为17cm．‎ 例4：如图，南北向MN为我国领域，即MN以西为我国领海，以东为公海.上午9时50分，我反走私A艇发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海开来，便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C两艇的距离是13海里，A、B两艇的距离是5海里；反走私艇测得离C艇的距离是12海里.若走私艇C的速度不变，最早会在什么时间进入我国领海？‎ 分析：为减小思考问题的“跨度”，可将原问题分解成下述“子问题”：（1）△ABC是什么类型的三角形？（2）走私艇C进入我领海的最近距离是多少？（3）走私艇C最早会在什么时间进入？这样问题就可迎刃而解.‎ 解：设MN交AC于E，则∠BEC=900.‎ 又AB2+BC2=52+122=169=132=AC2，‎ ‎∴△ABC是直角三角形，∠ABC=900.‎ 又∵MN⊥CE，∴走私艇C进入我领海的最近距离是CE，‎ 则CE2+BE2=144，（13-CE）2+BE2=25，得26CE=288，‎ ‎∴CE=. ÷≈0.85（小时）， 0.85×60=51（分）.‎ ‎9时50分+51分=10时41分.‎ 答：走私艇最早在10时41分进入我国领海.‎ ‎1．【答案】13或 ‎2．【答案】A ‎3、【答案】（1）2；（2）＝4或3，当＝4时，面积为12。‎ ‎4.【答案】B ‎5．【答案】‎ ‎6． 【答案】．‎ ‎7．【答案】‎ ‎8．【答案】‎ ‎9．【答案】10，（或）‎ ‎10、‎ C D B A E O ‎【答案】（1）由题意得B（3，1）．‎ 若直线经过点A（3，0）时，则b＝‎ 若直线经过点B（3，1）时，则b＝‎ 若直线经过点C（0，1）时，则b＝1‎ 1. 若直线与折线OAB的交点在OA上时，即1＜b≤，如图25-a，‎ 图2‎ ‎ 此时E（2b，0）‎ ‎∴S＝OE·CO＝×2b×1＝b ‎②若直线与折线OAB的交点在BA上时，即＜b＜，如图2‎ 此时E（3，），D（2b－2，1）‎ ‎∴S＝S矩－(S△OCD＋S△OAE ＋S△DBE )‎ ‎＝ 3－[(2b－1)×1＋×(5－2b)·()＋×3()]＝‎ ‎∴‎ ‎（2）如图3，设O1A1与CB相交于点M，OA与C1B1相交于点N，则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。‎ 图3‎ 由题意知，DM∥NE，DN∥ME，∴四边形DNEM为平行四边形 根据轴对称知，∠MED＝∠NED 又∠MDE＝∠NED，∴∠MED＝∠MDE，∴MD＝ME，∴平行四边形DNEM为菱形．‎ 过点D作DH⊥OA，垂足为H，‎ 由题易知，tan∠DEN＝，DH＝1，∴HE＝2，‎ 设菱形DNEM 的边长为a，‎ 则在Rt△DHM中，由勾股定理知：，∴‎ ‎∴S四边形DNEM＝NE·DH＝‎ ‎∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化，面积始终为．‎ B组 ‎1. A 2. 4 3. D 4. C 5. A ‎6. 析解：欲求正方体表面上点A与点B的最短路程，直接求解有困难，我们把以点A与点B为顶点的相邻的某两个正方形展开，得到一个长方形（如图2），由“两点之间线段最短”可知，“顽皮虫”在正方体表面上从点A爬到点B的最短路程是图2中线段AB的长．由勾股定理得，（cm）．‎ ‎7. 解：∵BC=10cm，D是BC的中点，∴BD=CD=5cm ‎ 又∵，即，∴△ABD是直角三角形，即AD⊥BC ‎ ∴△ACD也是直角三角形，，即 ‎9. 解：（1）因为，‎ ‎ 所以，这个三角形是直角三角形 ‎ （2）因为 ‎ 所以，这个三角形不是直角三角形 ‎10. 证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣A．‎ ‎∵S四边形ADCB=S△ACD+S△ABC=b2+aB．‎ 又∵S四边形ADCB=S△ADB+S△DCB=c2+a（b﹣a）‎ ‎∴b2+ab=c2+a（b﹣a）‎ ‎∴a2+b2=c2‎ 请参照上述证法，利用图2完成下面的证明．‎ 将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．‎ 求证：a2+b2=c2‎ 证明：连结　过点B作DE边上的高BF，则BF=b﹣a，　‎ ‎∵S五边形ACBED=　S△ACB+S△ABE+S△ADE=ab+b2+ab，　‎ 又∵S五边形ACBED=　S△ACB+S△ABD+S△BDE=ab+c2+a（b﹣a），　‎ ‎∴　ab+b2+ab=ab+c2+a（b﹣a），　∴a2+b2=c2．‎