六年级上册数学冀教版知识要点 15页

整理与评价 一、认识生活中圆形物品的面 1.生活中有些物品的面是圆形的,如硬币的面、钟表的面、圆 桌的面等等。 2.圆形物体在滚动时平稳。 3.圆是由曲线围成的封闭图形。 二、圆的对称性 1.圆是轴对称图形,圆的对称轴是圆的直径所在的直线。 2.任意一个圆都有无数条对称轴。 3.半圆只有一条对称轴。 4.圆的所有对称轴都相交于圆中心的一点。 三、认识圆心、圆的直径和圆的半径 1.把圆对折时,折痕的交点就是圆的圆心。一般用字母 O 表示。 2.通过圆心并且两端都在圆上的线段是圆的 直径,直径一般用字母 d 表示。 3.连接圆心和圆上任意一点的线段都是圆的 半径,半径一般用字母 r 表示。 4.任何一个圆都只有一个圆心。 5.直径是圆中最长的线段。 6.用直尺量出圆中最长的线段,这条线段就是圆的直径。这条 线段的中点就是这个圆的圆心。 四、圆的半径和直径的特征和它们之间的关系 1.任意一个圆都有无数条半径和无数条直径。 2.在同圆或等圆中,直径是半径的 2 倍,即 d=2r,r=2。 五、画出圆的半径和直径 1.画圆的半径时,连接圆心和圆上的任意一点 即可。 2.画圆的直径时,连接圆上的任意两点并且要 通过圆心。 六、用圆规画圆的方法和步骤 1.画圆的步骤: (1)把圆规的两脚分开,定好两脚之间的距离(半径); (2)把有针尖的一只脚固定在一点即圆心上; (3)把有铅笔尖的一只脚旋转一周就画出一个圆。 2.通过画圆得出结论:圆心决定圆的位置,半径决定圆的大小。 3.我国古代劳动人民使用“规”来画圆,使用“矩”画长方形、 正方形、直角等。 4.在一个正方形里画一个最大的圆,圆的直径等于正方形的边 要点提示: 圆形物品的面的边缘是由曲线围成 的。 易错点: 1.错误地以为直径是圆的对称轴。 2.错误地以为半圆也有无数条对称 轴。 易混点:圆的半径和直径都是一条线 段。 易错点:错误地以为通过圆心的线段 是直径。 重点:直径是圆中最长的线段。 易混点: 1.直径和半径的关系是在同圆或等 圆中进行研究和探讨的。 2.只有在同圆或等圆中,直径才是半 径的 2 倍,半径才是直径的一半。 易错点:画圆的半径或直径时,一般 要标出字母 r 或 d 以及圆心 O。 要点提示: 1.画圆时两固定一旋转。 2.画圆时,如果两个圆的圆心相同,则 这两个圆是同心圆。 关注微信公众号“捷思课堂”获取更多学习资料！ 第1页 长;在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。 七、图案设计 用圆规和直尺可以设计出许多美丽的图案。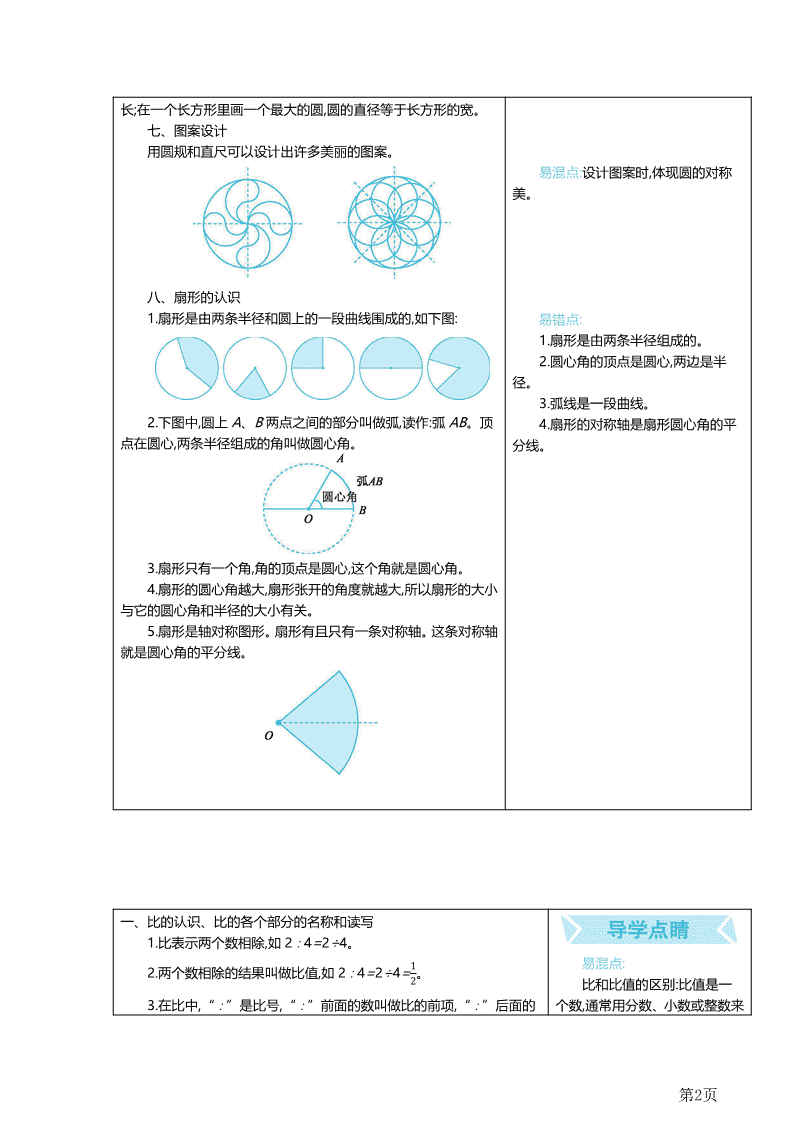 八、扇形的认识 1.扇形是由两条半径和圆上的一段曲线围成的,如下图: 2.下图中,圆上 A、B 两点之间的部分叫做弧,读作:弧 AB。顶 点在圆心,两条半径组成的角叫做圆心角。 3.扇形只有一个角,角的顶点是圆心,这个角就是圆心角。 4.扇形的圆心角越大,扇形张开的角度就越大,所以扇形的大小 与它的圆心角和半径的大小有关。 5.扇形是轴对称图形。扇形有且只有一条对称轴。这条对称轴 就是圆心角的平分线。 易混点:设计图案时,体现圆的对称 美。 易错点: 1.扇形是由两条半径组成的。 2.圆心角的顶点是圆心,两边是半 径。 3.弧线是一段曲线。 4.扇形的对称轴是扇形圆心角的平 分线。 一、比的认识、比的各个部分的名称和读写 1.比表示两个数相除,如 2∶4=2÷4。 2.两个数相除的结果叫做比值,如 2∶4=2÷4=12。 3.在比中,“∶”是比号,“∶”前面的数叫做比的前项,“∶”后面的 易混点: 比和比值的区别:比值是一 个数,通常用分数、小数或整数来 关注微信公众号“捷思课堂”获取更多学习资料！ 第2页 数叫做比的后项(比的后项不能是 0),比的前项除以比的后项所得的商叫 做比值。 2 ∶ 4 = 12 ︙ ︙ ︙ ︙ 前项 比号 后项 比值 4. 5∶10 读作“5 比 10”;4 比 5 写作“4∶5”。 二、比的各个部分和除法、分数的各个部分之间的关系 联系(相当于) 区别 比 比的前项 ∶比号 比的后项 比值 一种关系 除法 被除数 ÷除号 除数 商 一种运算 分数 分子 —分数线 分母 分数值 一种数 三、求比值的方法 1.求比值时,用比的前项除以比的后项所得的商,就是比值。如 5∶7=5÷7=57。 2.求比值是一种运算,结果是一个数,可以是整数也可以是小数,还可以 是分数。 四、比的基本性质与化简比 1.比的前项、后项同时乘或除以相同的数(0 除外),比值不变。这叫做 比的基本性质。 2.利用比的基本性质可以把一个比化成最简单的整数比。 3.化简比的方法: (1)两个整数的比:用比的前项和后项同时除以它们的最大公因数。 如 9∶12=(9÷3)∶(12÷3)=3∶4 (2)两个分数的比:用前项、后项同时乘分母的最小公倍数,再按化简整 数比的方法来化简(也可以用前项除以后项,但最后一定要写成比)。 如23∶25=(23×15)∶(25×15)=10∶6=5∶3 (3)两个小数的比:比的前、后项都扩大相同的倍数,先化成整数比,再化 简。 如 0.4∶0.06=(0.4×100)∶(0.06×100)=40∶6=20∶3 4.化简带单位的两个同类量的比时,先统一单位,再化简。 如 0.5 千米∶200 米=500∶200=5∶2 五、比例的意义、比和比例的区别 1.表示两个比相等的式子叫做比例。 2.判断两个比能否组成比例要看这两个比的比值是否相等。 3.比和比例的区别: 比 4∶6 由两个数组成,是一个式子,表示两个数相除 比例:2∶3=4∶6 由四个数组成,是一个等式,表示两个比相等 六、求比值与化简比的区别和联系 不同点 化简比 求比值 意义不同 化简比是把两个数的比化 成最简单的整数比,比的前 求比值是比的前项除以比 的后项所得的商 表示,比表示两个数的关系,不能 用小数或整数表示。 易错点:比的后项不能是 0。 要点提示: a∶b= =a÷b(b≠0) 易混点: 1.比和比值都可以用分数的 形式来表示,但是读法不一样。 2.比值是没有单位名称的。 重点: 最简整数比的前项和后项是 互质数。 要点提示: 1.体育比赛两队的分数比是 2∶0,这只是记分形式,不是相除 关系,不能化简。 2.化简比时,如果比的后项是 1,是不能省略的。 易错点: 判断两个比能否组成比例还 可以化简比。 易混点: 比的形式是式子,比例的形 式是等式。 易错点: 1.化简比的结果必须是个比; 求比值的结果是个数。 2.比值是一个数,化简比表示 两个数之间的关系。 关注微信公众号“捷思课堂”获取更多学习资料！ 第3页 项和后项是互质数 计算方法不同 化简比:是根据比的基本性 质,把比的前项、后项同时 乘或除以相同的数(0 除 外),化成最简比;如果所得 的整数比不是最简的,要连 续化简,化成最简的 求比值是用比的前项除以 后项所得的商,就是进行除 法运算 结果不同 化简比的结果是一个最简 单的整数比,比的前项、后 项是互质数 求比值的结果是一个数,这 个数可以是整数,可以是分 数,也可以是小数 七、比例的组成部分和各个部分的名称 组成比例的四个数,叫做比例的项。两端的两项叫做外项,中间的两项 叫做内项。如 八、比例的基本性质 1.在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性 质。 2.如果把比写成分数的形式,等号两端的分子和分母分别交叉相乘,它 们的积相等。 九、解比例 1.求比例中的未知项叫做解比例。解比例的依据是比例的基本性质。 2.解比例的方法:先根据比例的基本性质,把比例式转化为方程形式的 等积式,再求出未知项。 解比例: 十、按比例分配 1.按比例分配问题的特征:已知总量和部分量的比,求部分量是多少。 2.按比例分配问题的解答方法:先求总份数,再求各个部分占总量的几 分之几,最后用总量乘部分量占总量的几分之几求出各个部分量。 十一、按比例解答问题 要点提示: 1.分数形式的比例确定内项 和外项的方法: 2. 4 和 40 是外项,1.6 和 60 是内项。 易混点: 比的基本性质和比例的基本 性质是不同的,前者是前项和后 项之间的同时变化,后者是内项 和外项的积相等。 易错点: 1.解比例和解方程一样,不要 忘记写“解”。 2.解比例的依据是比例的基 本性质。 重点提示: 按比例分配问题就是把比例 问题转化为求一个数的几分之几 是多少来解答。 易错点: 用比例的知识解答问题时, 两个比的前项和后项的比不对 关注微信公众号“捷思课堂”获取更多学习资料！ 第4页 用比例知识解答问题时,要注意列出的比例中的每个比的前项和后项 的对应。 如:六(1)班男、女生人数的比是 5∶3,其中男生有 25 人,求女生有多少 人时,可以设女生有 x 人,然后利用数学的对应思想列出比例:5∶3=25∶x, 解之得 x=15。 十二、解决问题 解答连比的简单的按比例分配问题时的方法等同于两个数的比例的 按比例分配的解答方法:一是先求出总份数;二是求各个部分占总量的几分 之几;三是根据求一个数的几分之几是多少求出各个部分量。 如用 108 厘米长的铁丝做一个长方体框架,这个长方体框架长、宽、 高的比是 4∶2∶3,求这个长方体框架的长、宽和高分别是多少厘米。 4+2+3=9 长:108÷4×49=12(厘米) 宽:108÷4×29=6(厘米) 高:108÷4×39=9(厘米) 答:这个长方体框架的长、宽、高分别是 12 厘米、6 厘米和 9 厘米。 十三、测量旗杆的高度 在同一地点,同一时间测量的杆长和影长的比值是相等的,利用这个方 法可以测量高大物体的高度。解答此类问题应注意:旗杆的高度∶旗杆的 影长=竹竿的高度∶竹竿的影长。 例:在同一时刻同一地点,如果高为 2 米的测杆的影长为 2 米,那么影长 为 30 米的旗杆的高是多少米? 解:测竿的高度∶测竿的影长=旗杆的高度∶旗杆的影长,2∶2=30∶ 旗杆的高度。设旗杆的高度是 x 米,得比例:2∶2=30∶x。 解得旗杆的高度=30 m。 应。 易错点: 用按比例分配的知识解答连 比问题时,注意数量与份数的对 应。 重点提示: 同一时间、同一地点、竹竿 的高度和影长的比值是不变的。 一、百分数的意义和读写 1.表示一个数是另一个数的百分之几的数叫做百分数,百分数又叫“百 分率”或“百分比”。 2. “%”是百分号,读作百分之。 3.读百分数时,先读“%”,再读分子。如“30%”读作百分之三十。写 百分数时,读几写几,最后加上“%”。 4.百分数表示的是两个数之间的倍比关系,不能表示具体的数量,所以 百分数后面不能加单位名称。 如一条线段长 0.5 米,不能说一条线段长 50%米。 5.分母是 100 的分数并不是百分数,必须把分母写成“%”才是百分数, 所以“分母是 100 的分数就是百分数”这句话是错误的。 6.百分数和分数的区别和联系: (1)联系:都可以用来表示两个量之间的倍比关系。 (2)区别:意义不同,百分数只表示倍比关系,不表示具体数量,所以不能 易混点: 百分数表示两个数量之间 的倍比关系,分数可以表示倍比 关系,也可以表示数字。 注意点: “%”的两个 0 要 小写,不要与百分数前面的数混 淆。 重点提示: 1.把分数化成百分数时,用 分子除以分母,除不尽的时候商 保留三位小数,结果用“≈”连接, 关注微信公众号“捷思课堂”获取更多学习资料！ 第5页 带单位。 分数不仅表示倍比关系,还能带单位表示具体数量。百分数的分子可以 是小数,分数的分子只能是整数。 二、百分数与分数的互化和大小比较 1.分数化成百分数:可以把分数化成分母是 100 的分数,再化成百分数; 一般是把分数化成小数,除不尽时,保留三位小数,再把小数化成百分 数。如 225=2÷25=0.08=8% 23≈0.667=66.7% 2.百分数化成分数:把百分数写成分数的形式,能约分的要约成最简分 数。如 6%= 6100= 350 3.比较百分数和分数的大小时,可以把分数化成百分数,再比较大小;也 可以把百分数化成分数,再比较大小。 如比较45和 75%的大小。 方法一 把分数化成百分数:45=80% 80%>75%,所以45>75%。 方法二 把百分数 化成 分数: 75%= 75100 45= 8010075100< 80100,所以,75%<45。 三、百分数和小数的互化和求一个数是另一个数的百分之几 1.百分数化成小数:只要把百分号去掉,同时把小数点向左移动两位。 如 35%=0.35 2.小数化成百分数:只 要 把小数点向右移动两位,添上百分号即可。 如 0.24=24% 3.求一个数是另一个数的百分之几,用一个数除以另一个数,把计算结 果化成百分数。 如求 3 是 5 的百分之几,用 3÷5=0.6=60%。 4.求一个量是另一量的百分之几时,如果两个量单位名称不同,需要进 行单位转化,只有转化相同的单位后才可以进行解答。 如 30 厘米是 1 米的百分之几? 解答:1 米=100 厘米 30÷100= 30100=30% 答:30 厘米是 1 米的 30%。 四、百分率 1.求常见的百分率如达标率、及格率、成活率、发芽率、出勤率等求 百分率就是求一个数是另一个数的百分之几 。 发芽率= 发芽种子数 试验种子总数 ×100% 合格率= 合格数 总数 ×100% 含盐率= 盐的质量 盐水的质量 ×100% 出油率= 油的质量 原料的质量 ×100% 一般来讲,出勤率、成活率、合格率、正确率能达到 100%,出米率、出 油率达不到 100%,完成率、增长了百分之几等可以超过 100%。一般出粉 化成百分数时使用“=”连接。 2.把百分数化成分数,先把 百分数化成分母是 100 的分数 (如果分子是小数先化成整数), 再化成最简分数。 易错点: 1.把小数化成百分数:如果 是一位小数,位数不够,用 0 补 足。如果三位以上的小数化成百 分数,需要把小数保留三位,再化 成百分数。 2.百分数化成小数,位数不 够用 0 补足。 易错点:求各种百分率最后 都要乘 100%。 重点提示: 1.出勤率、发芽率等都是指 部分量占总量的百分比,所以最 高为 100%。 关注微信公众号“捷思课堂”获取更多学习资料！ 第6页 率在 70%到 80%,出油率在 30%到 40%。 2.我们求各种百分率时,如果题中给出的两种量的单位名称不同,需要 先统一单位名称,再计算百分率。如 例:1 吨小麦磨出面粉 750 千克,求小麦的出粉率。 1 吨=1000 千克 7501000×100%=75% 答:小麦的出粉率是 75%。 3.求较复杂的百分率问题时,一定要注意一般百分率是用部分量除以总 数量。 例: 六(1)班今天有 46 人来上课,有 2 人请事假,有 2 人请病假。求这一 天六(1)班的出勤率。 46+2+2=50(人) 4650×100%=92% 答:今天的出勤率是 92%。 五、百分数的简单应用 1.求一个数的百分之几是多少:用这个数乘百分之几。 例 1:某校一年级有 200 人,二年级学生数是一年级的 120 %,二年级有 学生多少人? 200×120%=240(人) 答:二年级有学生 240 人。 2.从生活中发现数学信息,提出数学问题,并尝试解决,综合运用所学知 识解决简单的实际问题。 2.求百分率时,注意部分量 除以总数量,再乘 100%。 重点提示: 求一个数的百分之几是多 少,用这个数乘百分之几。 一、圆的周长的认识 1.车轮滚动一周走的距离就是车轮的周长。 车轮每分前进米数(速度)=车轮的周长×转数 2.圆一周的长度就是圆的周长。 3.测量硬币的周长的方法有滚动法和绕绳法。 这两种方法体现了数学的“化曲为直”思想。 4.任何一个圆的周长总是它的直径的 3 倍多一些,这个倍数是一个 固定不变的数,我们把它叫做圆周率,用字母π表示。 约 2000 年前的中国古代《周髀算经》有“周三径一”的说法;约 1500 年前,数学家祖冲之计算出圆周率在 3.1415926 和 3.1415927 之 间。 5.任何一个圆的圆周率,都不随圆的大小而变化。 二、圆的周长计算公式(圆的周长和直径的关系) 1.如果用 C 表示圆的周长,则 C=πd 或 C=2πr。 例 1:已知圆的半径是 1 厘米,则根据 C=2πr 求出周长: 2×3.14×1=6.28(厘米) 例 2:已知圆的直径是 1 厘米,则根据 C=πd 求出周长: 3.14×1=3.14(厘米) 2.已知圆的周长,则圆的直径:d=C÷π,半径:r=C÷π÷2。 易错点: 1.错误地以为π=3.14。 2.错误地以为大圆的圆周率的 值就大,小圆的圆周率的值就小。 重点提示: π是一个无限不循环小数,计算 时,一般取 3.14。 易错点: 错误地以为半圆的周长就是该 圆的周长的一半。 重点提示: 如图,圆的直径越长,周长越长, 直径越短,周长越短。 关注微信公众号“捷思课堂”获取更多学习资料！ 第7页 例:已知圆的周长是 6.28 厘米,求圆的直径和半 径。 直径: 6.28÷3.14=2(厘 米) 半 径:6.28÷3.14÷2=1(厘米) 3.半圆的周长计算方法:C 半圆=π2 +d=πr+2r 例 1:已知半圆的直径是 2 厘米,求半圆的周长是多少厘米。 3.14×2÷2+2=5.14(厘米) 答:半圆的周长是 5.14 厘米。 例 2:已知半圆的半径是 1 厘米,求半圆的周长。 3.14×1+2×1=5.14(厘米) 答:半圆的周长是 5.14 厘米。 4.体会转化思想以及乘法分配律在圆的周长中的应用。 例:下面的两个小圆的周长的和与大圆的周长相比,哪个长?(单位: 厘米) 。3.14×6+3.14×10=3.14×(6+10),所以同样长。 三、圆的面积 1.一个圆所占的平面的大小叫做圆的面积。 2.把一个圆平均分成若干份(偶数份)后,可以拼成一个近似的长方 形,这个长方形的长是圆的周长的一半,宽是圆的半径,因为长方形的面 积=长×宽,所以圆的面积=2×r=2π2 ×r=πr2。 这一推导过程体现了数学的转化思想。 S = 2×r=2π2 ×r=πr2 例:已知圆的半径是 1 厘米,求圆的面积。 3.14×12=3.14(平方厘米) 答:圆的面积是 3.14 平方厘米。 3.半圆面积=圆面积÷2 公式:S=πr2÷2 四、圆的面积公式的应用 1.已知圆的直径,则圆的面积 S=π(d÷2)2。 例:已知圆的直径是 4 厘米,求圆的面积。 3.14×(4÷2)2=3.14×4=12.56(平方厘米) 2.已知圆的周长,则圆的面积 S=π(C÷π÷2)2。 例:已知圆的周长是 12.56 厘米,求圆的面积。 12.56÷3.14÷2=2(厘米) 3.14×22=12.56(平方厘米) 答:圆的面积是 12.56 平方厘米。 3.两个圆如果直径、半径、周长或面积其中一项相等,则其余几项 也都相等。 4.在一个正方形里画一个最大的圆(外方内圆),圆的直径等于正方 易混点: 错误地以为半径是 2 厘米的圆 的面积和周长是相等的。 重点提示: 圆的半径扩大到原来的 a 倍,直 径也扩大到原来的 a 倍,周长扩大到 原来的 a 倍,面积扩大到原来的 a2 倍。 重点提示: 周长相等的长方形、正方形和 圆,圆的面积最大。 重点提示: 圆环的面积实质是两个同心圆 的面积的差。 重点提示: 记住这些数据,计算起来简单 又快。 关注微信公众号“捷思课堂”获取更多学习资料！ 第8页 形的边长;在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。 5.周长相等的正方形和圆,圆的面积较大。 五、圆环 1.一个环形,外圆的半径是 R,内圆的半径是 r,它的面积 S=π(R2-r2) 或 S=πR2-πr2。 (其中 R=r+环的宽度) 2.常用的 3.14 的倍数: 3.14×2=6.28 3.14×3=9.42 3.14×4=12.56 3.14×5=15.7 3.14×6=18.84 3.14×7=21.98 3.14×8=25.12 3.14×9=28.26 3.14×12=37.68 3.14×14=43.96 3.14×16=50.24 3.14×18=56.52 3.14×24=75.36 3.14×25=78.5 3.14×36=113.04 3.常用的一些数的平方: 112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 192=361 202=400 一、求一个数比另一个数多(少)百分之几 1.求一个数比另一个数多百分之几,用(一个数-另一个数)÷另一个 数。 例:求 5 比 4 多百分之几? (5-4)÷4=1÷4=25% 2.求一个数比另一个数少百分之几,用(另一个数-一个数)÷另一个 数。 例:求 4 比 5 少百分之几? (5-4)÷5=1÷5=20% 3.已知整体和一部分,求另一部分占总量的百分之几,用(总量-部分 量)÷总量。 例:某车间上周计划生产 200 辆汽车,到周四只生产了 120 辆,还剩下 百分之几没有完成? (200-120)÷200=80÷200=40% 答:还剩下 40%没有完成。 二、求比一个数多(少)百分之几的数是多少 1.求比一个数多百分之几的数是多少,用这个数×(1+百分之几)。 例:比 5 多 20%的数是多少? 方法一:5+5×20%=5+1=6 方法二:5×(1+20%)=6 2.求比一个数少百分之几的数是多少,用这个数×(1-百分之几)。 例:求比 5 少 20%的数是多少? 方法一:5-5×20%=5-1=4 方法二:5×(1-20%)=4 三、已知比一个数多(少)百分之几的数是多少,求这个数 已知比一个数多(少)百分之几的数是多少,求这个数一般用方程的方 法来解答,解:设一个数是 x,然后列方程得:x±x%=多少数,最后列方程解 答。 例:六年级参加科技活动的有 48 人,比参加数学活动的少 20%,参加 数学活动的有多少人? 解:设参加数学活动的有 x 人。 重点提示: 一个数比另一数多(少)百分 之几,就是说这个数是另一个数的 (1±百分之几) 易错点: 错误地以为甲数比乙数多百 分之几,乙数就比甲数少百分之 几。 重点提示: 解答有关百分数的实际问题 时,如果单位“1”未知,我们可以 列方程解答。 关注微信公众号“捷思课堂”获取更多学习资料！ 第9页 (1-20%)x=48 0.8x=48 x=60 答:参加数学活动的有 60 人。 四、折扣 1.标价:商品摆放在柜台出售的价格,包括成本和利润两部分。 2.售价:商品的成交价格。售价经常等于或小于标价。 3.折扣:商品按原定价格的百分之几出售,叫做折扣。通称“打折”。 4.几折就表示十分之几,也就是百分之几十。几折用汉字表示。 例如:八折=80% 六折五=0.65=65% 5.解答折扣问题时,一般都把折扣转化为百分数,然后按照百分数问 题的解答方法来解答。 例: (1)一件上衣原价是 100 元,现价是 80 元,商家打几折促销? 80÷100=80% =八折 现价÷原价=折扣 (2)一件上衣原价 100 元,商家打八折促销,现价是多少元? 100×80%=80(元) 原价×折扣=现价 (3)一件上衣打八折促销是 80 元,原价是多少元? 80÷80%=100(元) 现价÷折扣=原价 6.打几折就是按原价的百分之几出售或说降价了(1-百分之几)出售。 例:一件上衣原价 200 元,打八折销售,降价了多少元? 200×(1-80%)=40(元) 答:降价了 40 元。 五、成数 1.几成就是十分之几,也就是百分之几十。 2.几成几表示百分之几十几。如三成五表示 35%。 3.求比一个数多几成的数是多少,用这个数×(1+成数)。 例:某村去年产玉米 300 吨,今年比去年增产两成,今年产玉米多少 吨? 300×(1+20%)=360(吨) 答:今年产玉米 360 吨。 4.求比一个数少几成的数是多少,用这个数×(1-成数)。 例:8 月份生产自行车 3000 辆,9 月份减产两成,9 月份生产自行车多 少辆? 3000×(1-20%)=2400(辆) 答:9 月份生产自行车 2400 辆。 六、税收 1.缴纳的税款叫做应纳税额。 2.应纳税额与各种收入的比率叫做税率。 3.求应纳税额实际上就是求一个数的百分之几是多少,用乘法计算。 例:某超市上个月的营业额是 3 万元,按 5%的税率缴纳营业税,需要纳 税多少元? 3 万元=30000 元 30000×5%=1500(元) 答:需要纳税 1500 元。 提示:应纳税额=营业额×税率 应纳税款÷税率=营业额 七、储蓄 1.存款分为活期、整存整取和零存整取等方法。 2.存入银行的钱叫做本金。 3.取款时,银行除本金外多付给的钱,叫做利息。 4.利率:利息占本金的百分率。按年计算的叫做年利率;按月计算的叫 易混点: “买几送几”也是折扣问题, 如“买四送一就是买 5 个花 4 个 的钱也就是打八折”。 重点提示: 解答成数问题时,一般把成数 转化为百分数来解答。 易混点: 应纳税额就是要缴纳的税款, 不同于营业额,它是营业额与税率 的乘积。 易错点: 本息和是本金与利息的和。求 关注微信公众号“捷思课堂”获取更多学习资料！ 第10页 做月利率。 5.利息=本金×利率×存期 本息和=本金+利息 6.存款到期时,银行给付的钱应该是本息和。 例:妈妈在 2012 年 7 月 10 日把 10000 元钱存入银行,存期 3 年,当 时的年利率是 4.25%,到期时,妈妈取回多少元钱? 10000×4.25%×3+10000=1275+10000=11275(元) 答:到期时,妈妈取回 11275 元钱。 八、学会理财 1.学会从数学主题图和文字中发现信息和要解决的问题,并能自己设 计存钱计划和对计划作出合理解释。 2.经历设计储蓄方案、优化方案的过程,学会用数学的眼光观察和解 决生活中的数学问题,提高自己的数学素养。 本息和时,只计算出利息忘记加本 金。 重点提示: 定期存款,一次性存期越长,利 息越多。 一、放大与缩小 1.放大镜可以把字放大,照片可以把景物缩小。 2.复印机可以放大也可以缩小,放映机可以把胶片上的画面放大。 3.把第一个图形的边长放大到原来的 2 倍后可以得到第二个图形,还 可以说把第二个图形缩小到原来的12后得到第一个图形。 4.把一个图形放大或 缩小后得到的图形与原 图形相比,形状相同,大小 不同。 5.放大与缩小的相同点和不同点。 相同点 边的长度按一定的比放大或缩小,图形的大小发 生变化,形状不变。比的前项表示变化的长度,比 的后项表示原来的长度 不同点 比值大于 1(如 2∶1)表示图形放大,比值小于 1(如 1∶3)表示图形缩小 6.如果一个长方形的各边长度扩大到原来长度的 n 倍或缩小到原来 长度的 1n,那么它的周长就扩大到原来长度的 n 倍或缩小到原来长度的1n, 它的面积就扩大到原来的 n2 倍或缩小到原来的 1n2 。 二、画放大与缩小后的图形 在方格纸上按一定的比例将图形放大或缩小分为三步: 一看:看原图形每边各占几格; 二算:计算按给定的条件将图形的各边长放大或缩小后得到的新图形 每边各占几格; 三画:按计算出的边长画出原图形的放大图或缩小图。 易错点: 1.错误地以为图形放大或缩 小后,形状会改变。 2.错误地以为图形每边扩大 到原来的 n 倍后,面积也扩大到 原来的 n 倍。 重点提示: 画放大或缩小后的图形时, 确定所画图形的每个顶点的位置 和每边长是关键。 易混点:在比例尺中,比的前 关注微信公众号“捷思课堂”获取更多学习资料！ 第11页 三、比例尺的认识 1.画出的图形如果与原来的图形完全一样,我们可以说画出的图形与 原来的图形的比是 1∶1。 2.如果用图上 1 厘米表示实际的 10 厘米,我们就说这幅图的比例尺是 1∶10。 3.比例尺 1∶10,就是把原来的图形按 110缩小画出,或者说实际的 10 厘 米用图上的 1 厘米来表示。 四、比例尺的应用 1.比例尺就是图上距离和实际距离的比。 图上距离∶实际距离=比例尺或 图上距离 实际距离 =比例尺 2.利用比例尺和图上距离求实际距离: 例:在比例尺是 1∶1000 的图纸上,量得操场的长是 20 厘米,你知道操 场的实际长度吗? 方法一:图上长 20 厘米,实际长 20×1000=20000(厘米)=200(米) 方法二:20÷ 11000=20×1000=20000(厘米)=200(米) 答:操场的实际长度是 200 米。 实际距离=图上距离÷比例尺或者先明确图上 1 厘米表示实际的米或 千米数后,乘图上距离。 3.比例尺是一个比,他表示图上距离和实际距离的倍比关系,因此不能 带计量单位。(计算时要先统一单位) 五、线段比例尺 1.比例尺可以分为数值比例尺和线段比例尺。数值比例尺如 1∶100000;线段比例尺如 。 2.线段比例尺和数值比例尺之间的互化。 3.利用线段比例尺解答简单的实际问题:描述物体的方向和实际距离。 例: 一辆汽车正在向正南方向行驶。从上图看: (1)城市甲在汽车(南偏西 45°)方向上,与汽车的实际距离是(50)千米。 (2)城市乙在汽车(正东)方向上,与汽车的实际距离是(30)千米。 六、线段比例尺的应用 运用线段比例尺结合图上距离,可以求路程也可以求出图形的面积。 项如果是 1,这个比例尺是缩小比 例尺,如果后项是 1,这个比例尺 是扩大比例尺。 易错点: 错误地以为比例尺是图上距 离和实际距离的比值。 重点提示: 比例尺是图上距离比实际距 离得到的最简整数比,可以写成 带比号的形式,也可以写成分数 的形式。 重点提示: 应用线段比例尺画图时,要 先求出图上距离,再根据图上距 离画出相应的平面图,并标明平 面图的名称及比例尺。 易错点: 无论是求路程还是求面积, 注意不同单位之间的转化。 关注微信公众号“捷思课堂”获取更多学习资料！ 第12页 例:有一块长方形空地,长 200 米,宽 150 米,在一张平面图上用 4 厘米 的线段表示长,把这块长方形空地画在纸上后的面积是多少平方厘米? 4 厘米∶200 米=4 厘米∶20000 厘米=1∶5000 150 米=15000 厘米 15000× 15000=3(厘米) 4×3=12(平方厘米) 答:把这块长方形空地画在纸上后的面积是 12 平方厘米。 一、认识扇形统计图 1.扇形统计图:用整个圆的面积表示总数,用圆内各个扇形的 面积表示各部分数量同总数之间的关系,也就是各部分数量占总 数的百分比。 2.扇形统计图的特点: (1)用扇形的面积表示部分占总体的百分比; (2)扇形统计图的各部分占总体的百分比之和为 100%或 1。 二、读扇形统计图 我们可以从扇形统计图获取信息,先与整体比较,看看部分占 整体的百分比是多少,再看一下各部分之间谁占的百分比大,在此 基础上仔细分析,得出结论。 例:幸福一小六年级同学参加课外兴趣小组的情况如下图,请 你看图回答问题。 (1)(电脑)小组最受欢迎,(绘画)小组与(歌唱)小组受欢迎程度 差不多。 (2)图中是把(六年级学生总人数)看作单位“1”。 (3)外语小组占(25)%,绘画小组比歌唱小组多总数的(1)%。 三、选择合适的统计图表示数据 1.常用统计图的优点: (1)条形统计图:可以清楚地看出各种 数量的多少。 (2)折线统计图:不仅可以看出各种数 量的多少,还可以清晰地看出数量的增减 变化情况。 (3)扇形统计图:能够清楚地反映出各 部分数量同总数之间的关系。 条形统计图 折线统计图 扇形统计图 特点 用一个单位长度表示一定的数量 用整个圆的面积表 示总数,用圆内的扇 形面积表示各部分 占总数的百分数 用直线的长短表示 数量的多少 表示数量的增减变 化 作用 从图中能清楚地看 出各数量的多少,便 于相互比较 从图中能清楚地看 出数量增减变化的 情况,也能看出数量 的多少 从图中能清楚地看 出各部分与总数的 百分比,以及部分与 部分之间的关系 四、制作扇形统计图的步骤 1.根据统计资料,整理数据,并计算出部分占整体的百分数。 重点提示: 扇形统计图能清楚地显 示每组数据相对于总体的百 分比。 易错点: 两个不同单位“1”的扇 形统计图无法比较数量的多 少。 重点提示: 选择统计图时,要结合需 要反映的数据的特征来进行 选择。 易错点: 注意每个扇形与部分量 的对应。 关注微信公众号“捷思课堂”获取更多学习资料！ 第13页 2.根据各部分占总体的百分数,计算出各部分扇形圆心角的 度数。 3.取适当半径作圆,按圆心角将圆分成几个扇形。 4.对应标上各部分名称及占总体的百分数。 一、找次品 1.找次品分组原则:把待测物品分成 3 份。能平均分就平均分成 3 份;不能平均分的, 应让多的与少的一份只相差 1。这样才能保证称的次数最少就能找出次品。 2.画“次品树形”分组图。 例: 27 个物品中有 1 个次品,最少称几次能找出次品? 分组 27÷3=9 由此分为 9,9,9 这三组。 (2)画“次品树形” 分组图,由此得出至少需 3 次。 3.用天平找次品时,所测物品与测试的次数有以下关系(只含 一个次品,已知次品比正品轻或重): 要辨别的物品的数目 保证能找出次品需要测的次数 2~3 1 4~9 2 10~27 3 28~81 4 82~243 5 …… …… 总结:称 n 次,最多可以分 3 的 n 次方个物品数目。(3 的 n 次方表示 n 个 3 相乘) 二、生活中的推理 1.判断正方体面上对应的数字时,应先从两次都看到的面开始分析,可以使用“排除 法”等方法。 例:一个正方体,每个面上分别写着数字 1~6,有一个人从不同的角度观察到下图的情 况,问这个正方体上相对的两个面上的数字各是几? 1 的对面是 5,2 的对面是 6,3 的对面是 4。 2.在判断名次的推理问题中,可以用排除法来解决。 例:王老师、陈老师和李老师是学校的三位老师,他们分别教美术、体育、音乐中的一 门课。王老师不会画画,李老师不会唱歌也不会画画。你知道他们分别教什么课吗? 解:李老师不会画画也不会唱歌,那他只能教体育,王老师不会画画,只能教音乐,剩下 重点提示: 2~3 个物体, 保证能找出次品 需要测的次数是 1 次;4~9 个物体 (2 次);10~27 个 物体(3 次)。 易错点: 相对面不相 邻,相邻面不相 对。 关注微信公众号“捷思课堂”获取更多学习资料！ 第14页 的美术就是陈老师教了。 关注微信公众号“捷思课堂”获取更多学习资料！ 第15页