北师大版六年级下册数学圆柱的体积课件 23页

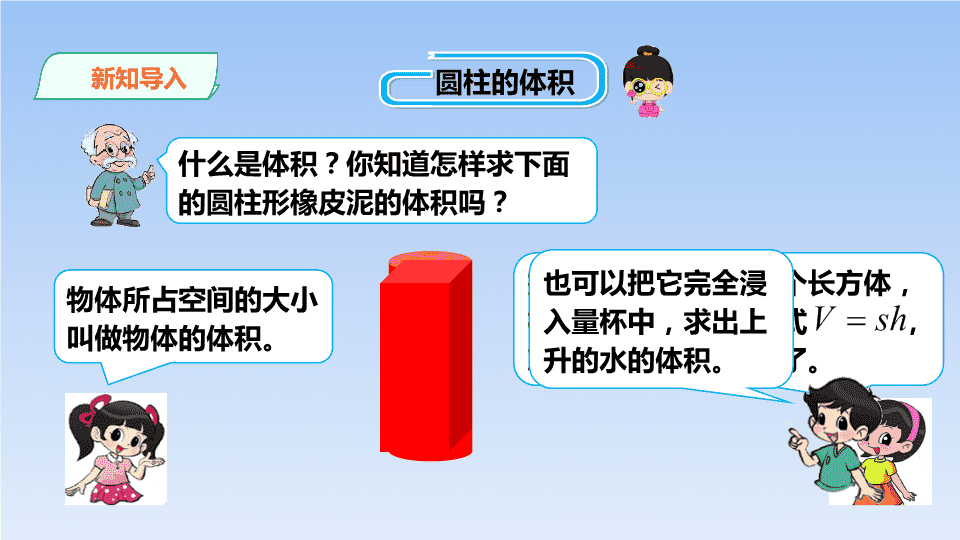
圆柱的体积 数学北师大版 六年级下 新知导入 圆柱的体积 什么是体积？你知道怎样求下面的圆柱形橡皮泥的体积吗？ 物体所占空间的大小叫做物体的体积。 把这块橡皮泥捏成一个长方体，根据长方体的体积公式 ，就可以求出它的体积了。 也可以把它完全浸入量杯中，求出上升的水的体积。 新知导入 圆柱的体积 这么粗的柱子，需要多少木材呢？ 一个杯子能装多少毫升水呢？ 实际上都需要求圆柱的体积。 想一想，怎样计算圆柱的体积？ 新知讲解 圆柱的体积 长方体和正方体的体积都等于 “ 底面积×高 “ 。 我猜想圆柱的体积也可能等于 ” 底面积×高 “ 。 想一想，怎样计算圆柱的体积？ 新知讲解 圆柱的体积 小组活动。（ 5 分钟） 尝试验证你的猜想，并与同伴交流。 新知讲解 圆柱的体积 尝试验证你的猜想，并与同伴交流。 从叠硬币来看，用 “ 底面积×高 ” 能计算出圆柱的体积。 能不能用圆面积的推导方法，推导出圆柱的体积公式呢？ 新知讲解 圆柱的体积 把圆柱等分成若干份，拼成一个近似的长方体。 长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高。 长方体的体积 = 底面积 × 高 圆柱的体积 = 底面积×高 高 高 底面积 底面积 新知讲解 圆柱的体积 长方体的长等于圆柱底面周长的一半。 长方体的宽等于圆柱的底面半径，长方体的高等于圆柱的高。 圆柱底面周长的一半 底面半径 圆柱的高 圆柱的体积 = 底面积×高 新知讲解 圆柱的体积 一根柱子的底面半径为 0.4m ，高为 5m 。 一根柱子的体积的多少立方米？ =3.14×0.4 2 ×5 ＝ 3.14×0.16×5 ＝ 3.14×0.8 ＝ 2.512 （ m 3 ） 答：一根柱子的体积 2.512m 3 。 新知讲解 圆柱的体积 从水杯里面量，水杯的底面直径是 6cm ，高是 16cm ，这个水杯能装多少毫升水？ =3.14× （ 6÷2 ） 2 ×16 ＝ 3.14×9×16 ＝ 452.16 （ cm 3 ） ＝ 452.16 （毫升） 答：这个水杯能装 452.16 毫升水。 新知讲解 圆柱的体积 可以根据底面周长求出底面半径，再求底面积。 先要算出底面的面积，再求金箍棒的体积。 金箍棒底面周长是12.56cm，长是200cm。这根金箍棒的体积是多少立方厘米？ 底面半径： 12.56÷3.14÷2 ＝ 2 （ cm ） 底面积： 3.14×2 2 ＝ 12.56 （ cm² ） 体积： 12.56×200 ＝ 2512 （ cm 3 ） 答：这根金箍棒的体积是 2512cm 3 。 新知讲解 圆柱的体积 求这根金箍棒的重量，用乘法计算。 如果这根金箍棒是铁制的，每立方厘米的铁重7.9g，这根金箍棒重多少千克？ 7.9×2512 ＝ 19844.8 （克）＝ 19.8448 （千克） 答：这根金箍棒重 19.8448 千克。 新知讲解 圆柱的体积 知识巧记 公式推导需转换， 分切拼图把形变 。 底面相等形异同，体积不变是关键。 计算方法无更新， 底面乘高 体积现。 课堂练习 你会做吗？ 1.一个圆柱形 盒子 的 底 面半径是5厘米，高是20厘米，它的 体 积是多少立方厘米？  先求这个盒子的底面积，再求它的体积。 3.14×5 2 ×20 ＝ 3.14×25×20 ＝ 1570 （ cm 3 ） 答：它的体积是 1570cm³ 。 课堂练习 你会做吗？ 2. 一个圆柱形水杯高 12 厘米，体积是 339.12 立方厘米，这个水杯的底面积是多少平方厘米？ 圆柱的体积 = 底面积×高，圆柱的底面积 = 体积÷高。 339.12 ÷ 12=28.26 （平方厘米） 答：这个水杯的底面积是 28.26 平方厘米。 课堂练习 你会做吗？ 3. 一个圆柱形零件，这个零件的体积是 628 立方厘米，底面积是 78.5 平方厘米，这个零件有多高？ 圆柱的体积 = 底面积×高，圆柱的高 = 体积÷底面积。 628 ÷ 78.5=8 （厘米） 答：这个零件高 8 厘米。 拓展提高 你会做吗？ 1. 把一个棱长为 10 厘米的正方体木块削成一个最大的圆柱，这个圆柱的体积是多少立方厘米？ 圆柱的底面直径等于正方体的棱长。 底面积： 3.14 ×（ 10 ÷ 2 ） ²=78.5 （ cm² ） 体积： 78.5 × 10=785 （ cm³ ） 答：这个圆柱的体积是 785 立方厘米。 圆柱的高也等于正方体的棱长。 拓展提高 你会做吗？ 2. 一个底面积是 2000 平方厘米，高是 40 厘米的圆柱形鱼缸，现在水深 25 厘米。放入几条金鱼后，水面上升了 4 厘米。这几条金鱼的体积是多少立方厘米？ 这几条金鱼的体积就是上升的水的体积。 25 厘米 4 厘米 2000 × 4=8000 （立方厘米） 答：这几条金鱼的体积是 8000 立方厘米。 拓展提高 你会做吗？ 3. 小刚要用一张长 18.84 厘米，宽 12.56 厘米的长方形纸围成一个圆柱，怎样围体积最大？ 以 18.84 厘米为底面周长，以 12.56 厘米为高，围成一个圆柱。 18.84cm 12.56cm 底面周长： 18.84cm 底面半径： 18.84 ÷ 3.14 ÷ 2=3 （厘米） 圆柱体积： 3.14 × 3² × 12.56 = 3.14 × 9 × 12.56 =354.9456 （立方厘米） 拓展提高 你会做吗？ 3. 小刚要用一张长 18.84 厘米，宽 12.56 厘米的长方形纸围成一个圆柱，怎样围体积最大？ 以 12.56 厘米为底面周长，以 18.84 厘米为高，围成一个圆柱。 18.84cm 12.56cm 底面周长： 12.56cm 底面半径： 12.56 ÷ 3.14 ÷ 2=2 （厘米） 圆柱体积： 3.14 × 2² × 18.84 = 3.14 × 4 × 18.84 =236.6304 （立方厘米） 354.9456 ＞ 236.6304 答：以 18.84 厘米为底面周长，以 12.56 厘米为高时，围成的圆柱体积最大。 课堂总结 这节课你学会了什么？ 02 圆柱的体积 = 底面积×高，用字母表示为 。 01 把圆柱拼成一个长方体，长方体的长等于圆柱底面周长的一半，宽等于圆柱的底面半径，高等于圆柱的高。 03 已知 V 、 s 、 h 三个量中的任意两个量，都可以根据公式求出第三个量，即 ， 。 板书设计 圆柱的体积 长方体的体积 = 底面积 × 高 圆柱的体积 = 底面积×高 作业布置 完成教材 10 页 4 、 5 、 6 、 7 题。