六年级下册数学试题-小升初数学模拟试卷（二）（PDF版含答案）全国通用 4页

小升初数学模拟试卷（二） （满分：１００分　时间：６０分钟） 一、选择题（每小题 ３分，共 １５分） １．（比例尺）在一幅地图上，用 ５厘米表示实际距离 １５０千米，则这幅地图的比例尺是（　　）。 Ａ．１ ３０　　　　　　　　Ｂ． １ ３０００　　　　　　　　Ｃ． １ ３００００００　　　　　　　　Ｄ． １ ３０００００ ２．（圆柱与圆锥）一个圆柱的底面周长是圆锥底面周长的 ４ ３，如果圆柱的体积和圆锥的体积相等，那 么圆柱的高是圆锥高的（　　）。Ａ．１６ ２７Ｂ．１ ３ Ｃ．９ ４８ Ｄ．３ １６ ３．（乘法原理）我校四名同学报名参加跳绳、跳远和跳高比赛，每人限报一个项目，共有（　　）种报名 方法。 Ａ．１２ Ｂ．１６ Ｃ．６４ Ｄ．８１ ４．（平均数问题）６名裁判给一名体操运动员打分，去掉一个最高分，平均得 ９分，去掉一个最低分，平 均得 ９．５分，则最高分与最低分相差（　　）。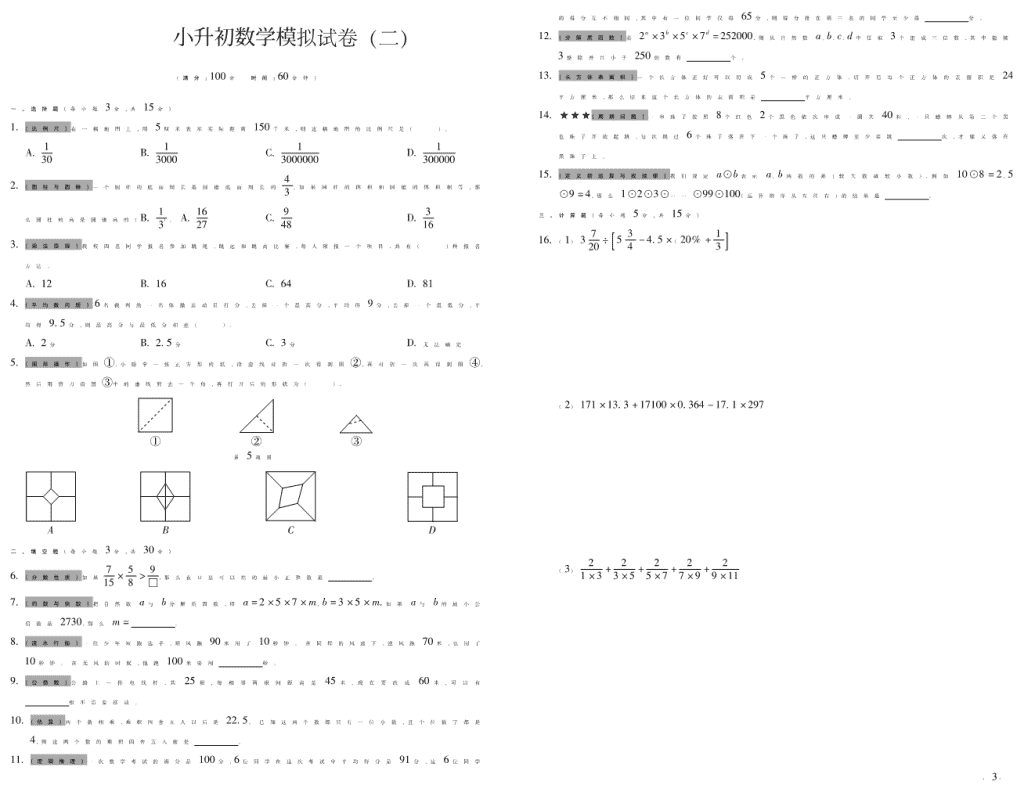 Ａ．２分 Ｂ．２．５分 Ｃ．３分 Ｄ．无法确定 ５．（图形操作）如图①，小聪拿一张正方形的纸，沿虚线对折一次得到图②，再对折一次再得到图④， 然后用剪刀沿图③中的虚线剪去一个角，再打开后的形状为（　　）。 ① 　　　　　　 ② 　　　　　　 ③ 第 ５题图 Ａ Ｂ Ｃ Ｄ 二、填空题（每小题 ３分，共 ３０分） ６．（分数性质）如果 ７ １５×５ ８＞９ □，那么在口里可以填的最小正整数是 。 ７．（约数与倍数）把自然数 ａ与 ｂ分解质因数，得 ａ＝２×５×７×ｍ，ｂ＝３×５×ｍ．如果 ａ与 ｂ的最小公 倍数是 ２７３０，那么 ｍ＝ 。 ８．（流水行船）一位少年短跑选手，顺风跑 ９０米用了 １０秒钟。在同样的风速下，逆风跑 ７０米，也用了 １０秒钟。在无风的时候，他跑 １００米要用 秒。 ９．（公倍数）公路上一排电线杆，共 ２５根，每相邻两根间距离是 ４５米，现在要改成 ６０米，可以有 根不需要移动。 １０．（估算）两个数相乘，乘积四舍五人以后是 ２２．５。已知这两个数都只有一位小数，且个位数字都是 ４，则这两个数的乘积四舍五入前是 。 １１．（逻辑推理）一次数学考试的满分是 １００分，６位同学在这次考试中平均得分是 ９１分，这 ６位同学 的得分互不相同，其中有一位同学仅得 ６５分，则得分排在第三名的同学至少得 分。 １２．（分解质因数）若 ２ａ×３ｂ×５ｃ×７ｄ＝２５２０００，则从自然数 ａ、ｂ、ｃ、ｄ中任取 ３个组成三位数，其中能被 ３整除并且小于 ２５０的数有 个。 １３．（长方体表面积）一个长方体正好可以切成 ５个一样的正方体，切开后每个正方体的表面积是 ２４ 平方厘米，那么原来这个长方体的表面积是 平方厘米。 １４．★★★（周期问题）一串珠子按照 ８个红色 ２个黑色依次串成一圈共 ４０粒，一只蟋蟀从第二个黑 色珠子开始起跳，每次跳过 ６个珠子落在下一个珠子，这只蟋蜱至少要跳 次，才能又落在 黑珠子上。 １５．（定义新运算与找规律）我们规定 ａ⊙ｂ表示 ａ，ｂ两数的差（较大数减较小数），例如 １０⊙８＝２，５ ⊙９＝４，那么 １⊙２⊙３⊙……⊙９９⊙１００（运算顺序从左往右）的结果是 。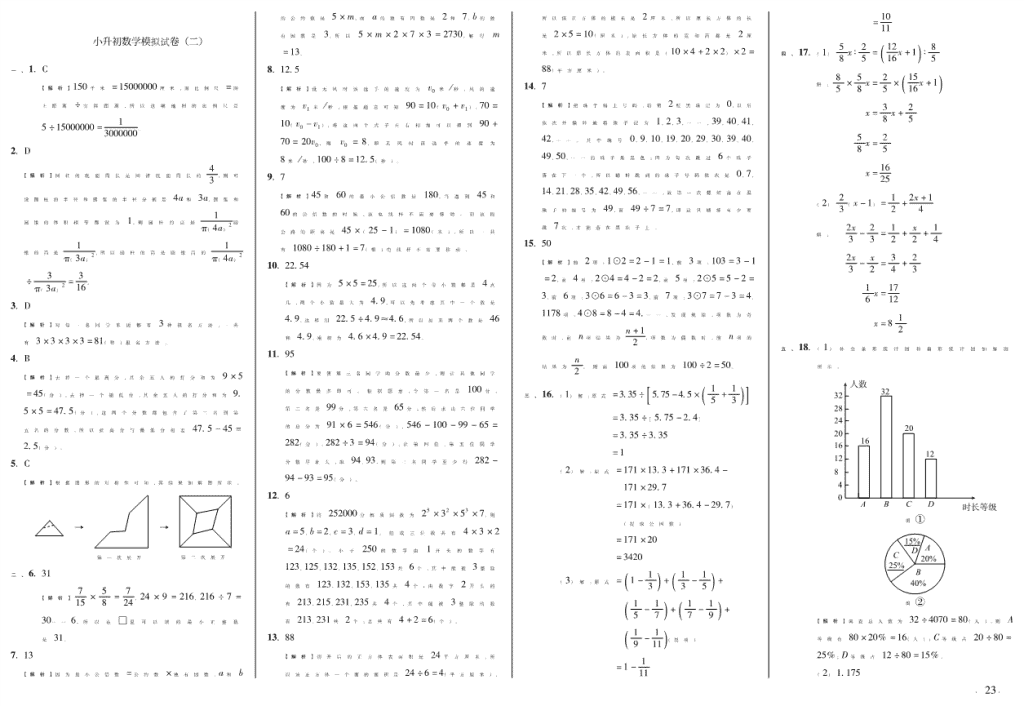 三、计算题（每小题 ５分，共 １５分） １６．（１）３７ ２０÷ ５３ ４－４．５×（２０％ ＋[ ]１ ３ （２）１７１×１３．３＋１７１００×０．３６４－１７．１×２９７ （３） ２ １×３＋ ２ ３×５＋ ２ ５×７＋ ２ ７×９＋ ２ ９×１１ ·３· 四、解方程（每小题 ５分，共 １０分） １７．（１）５ ８ｘ∶２ ５＝ １５ １６ｘ( )＋１ ∶８ ５　　　　　　　（２）２ ３（ｘ－１）＝１ ２＋２ｘ＋１ ４ 五、解答题（每小题 ６分，共 ３０分） １８．（统计圈）为了方便市民出行，截至 ２０１７年 ６月 ３０日，西安城市公共自行车公司投用自行车 ５２０００ 辆。小凡为了了解西安某公司员工平均每天使用公共自行车时间的情况，随机抽取了若干名该公 司员工进行调查，之后将这些员工每天使用公共自行车的时间（使用时间分为四个等级：“Ａ－０．５ 小时”“Ｂ－１小时”“Ｃ－１．５小时”“Ｄ－２小时”）进行了统计，并将结果绘制成两幅不完整的统 计图。 某公司员工平均每天使用公共自行车时间统计图 图① 　　　　 图② 第 １８题图 请你根据以上信息，解决下列问题： （１）补全条形统计图和扇形统计图。 （２）所抽取的员工平均每天使用公共自行车的时间为 小时。 （３）若该公司有 ６５０名员工，估算该公司员工中每天使用公共自行车时间超过 １小时的人数。 １９．（分数应用）袋子里装有若干个红、黑、白三种颜色的彩球，已知红球的数量是总数的 １ ３，增加了 ６ 个同样的红球后，红球的数量占总数的 １ ２，原来黑球数量为 ８个，则原来白球的数量为多少个？ ２０．（行程问题）甲、乙两人骑车分别从 Ａ、日两地相向而行，已知甲、乙两人的速度比是 ２∶３，甲比乙早 出发 １５分钟，且经过 １小时 ４５分钟遇见乙，此时甲比乙少走了 ６千米。求 Ａ、Ｂ两地之间的距离？ ２１．（经济问题）菜商店购进了一批钢笔，决定以每支 ９．５元的价格出售。第一个星期卖出了 ６０％，这 时还差 ８４元收回全部成本。又过了一个星期后全部售出，总共获得利润 ３７２元。那么商店购进 这批钢笔的价格是每支多少元？ ２２．（工程问题）甲、乙两人共同接受一批零件的加工任务，两人合作 １１天可完成，结果两人合作了 ７ 天后，乙另有任务，剩下的由甲单独做。如果甲仍按原来的工效，还需 ７天完成。为了能如期完成 任务，甲单独做时采用了新技术，使工效提高了 ８０％，这样不仅如期完成任务，还多做 ４个零件， 问原计划一共要加工多少个零件？ ·４· 小升初数学模拟试卷（二） 一、１．Ｃ 【解析】１５０千米 ＝１５００００００厘米，而比例尺 ＝图 上距离 ÷实际距离，所以这幅地图的比例尺是 ５÷１５００００００＝ １ ３００００００。 ２．Ｄ 【解析】圆柱的底面周长是圆锥底面周长的 ４ ３，则可 设圆柱的半径和圆锥的半径分别是 ４ａ和 ３ａ，圆锥和 圆锥的体积相等都设为 １，则圆柱的高是 １ π（４ａ）２圆 锥的高是 １ π（３ａ）２，所以圆柱的高是圆锥高的 １ π（４ａ）２ ÷ ３ π（３ａ）２ ＝３ １６。 ３．Ｄ 【解析】对每一名同学来说都有 ３种报名方法，一共 有 ３×３×３×３＝８１（种）报名方法。 ４．Ｂ 【解析】去掉一个最高分，其余五人的打分和为 ９×５ ＝４５（分），去掉一个撮低分，其余五人的打分和为 ９． ５×５＝４７．５（分），这两个分数都包含了第二名到第 五名的分数，所以蛙高分与最低分相差 ４７．５－４５＝ ２．５（分）。 ５．Ｃ 【解析】根据图形的对称性可知，其结果如解图所示。 　　 第一次展开 　　 第二次展开 二、６．３１ 【解析】７ １５× ５ ８ ＝ ７ ２４，２４×９＝２１６，２１６÷７＝ ３０……６，所以 在 □ 里 可 以 填 的 最 小 正 整 数 是 ３１。 ７．１３ 【解析】因为最小公倍数 ＝公约数 ×独有因数，ａ和 ｂ 的公约数是 ５×ｍ，而 ａ的独有因数是 ２和 ７，ｂ的独 有因数是 ３，所以 ５×ｍ×２×７×３＝２７３０，解得 ｍ ＝１３。 ８．１２．５ 【解析】设无风时该选手的速度为 ｖ０ 米／秒，风的速 度为 ｖ１ 米／秒，根据题意可知 ９０＝１０（ｖ０ ＋ｖ１），７０＝ １０（ｖ０ －ｖ１），将这两个式子左右相加可以得到 ９０＋ ７０＝２０ｖ０，则 ｖ０ ＝８，即无 风 时 该 选 手 的 速 度 为 ８米／秒，１００÷８＝１２．５（秒）。 ９．７ 【解析】４５和 ６０的最小公倍数是 １８０，当遇到 ４５和 ６０的公倍数的时候，该电线杆不需要移动。而该段 公路的距离是 ４５×（２５－１）＝１０８０（米），所以一共 有 １０８０÷１８０＋１＝７（根）电线杆不需要移动。 １０．２２．５４ 【解析】因为 ５×５＝２５，所以这两个带小数都是 ４点 几，两个小数最大为 ４．９，可以先考虑其中一个数是 ４．９，这样用 ２２．５÷４．９≈４．６，所以原来两个数是 ４６ 和 ４．９，乘积为 ４．６×４．９＝２２．５４。 １１．９５ 【解析】要使第三名同学昀分数最少，则让其他同学 的分数最多即可。根据题意，令第一名是 １００分， 第二名是 ９９分，第六名是 ６５分；然后求出六位同学 的总分为 ９１×６＝５４６（分），５４６－１００－９９－６５＝ ２８２（分），２８２÷３＝９４（分），让第四位、第五位同学 分数尽址大，取 ９４、９３，则第三名同学至少得 ２８２－ ９４－９３＝９５（分）。 １２．６ 【解析】将 ２５２０００分解质因数为 ２５ ×３２ ×５３ ×７，则 ａ＝５，ｂ＝２，ｃ＝３，ｄ＝１。组成三位数共有 ４×３×２ ＝２４（个）。小 于 ２５０的 数 字 由 １开 头 的 数 字 有 １２３，１２５，１３２，１３５，１５２，１５３共 ６个，其中能被 ３整除 的数有 １２３，１３２，１５３，１３５共 ４个；由数字 ２开头的 有 ２１３，２１５，２３１，２３５共 ４个，其中能被 ３整除的数 有 ２１３，２３１共 ２个；总共有 ４＋２＝６（个）。 １３．８８ 【解析】切开后的正方体表面积是 ２４平方厘米，所 以该正方体一个面的面积是 ２４÷６＝４（平方厘米）， 所以该正方体的棱长是 ２厘米，所以原长方体的长 是 ２×５＝１０（厘米），原长方体的宽和高都是 ２厘 米，所以原长方体的表面积是（１０×４＋２×２）×２＝ ８８（平方厘米）。 １４．７ 【解析】把珠于编上号码，将第 ２粒黑珠记为 ０，以后 依次并循环地将珠子记为 １，２，３，……，３９，４０，４１， ４２，……。其中编号 ０，９，１０，１９，２０，２９，３０，３９，４０， ４９，５０，……的珠子是黑色；因为每次跳过 ６个珠子 落在下一个，所以蟋蚌跳到的珠子号码依次是 ０，７， １４，２１，２８，３５，４２，４９，５６，……，故第一次螺蚌落在黑 珠子的编号为 ４９，而 ４９÷７＝７，即这只蟋蚌至少要 跳 ７次，才能落在黑珠子上。 １５．５０ 【解析】前 ２项：１⊙２＝２－１＝１，前 ３项：１０３＝３－１ ＝２，前 ４项：２⊙４＝４－２＝２，前 ５项：２⊙５＝５－２＝ ３，前 ６项：３⊙６＝６－３＝３，前 ７项：３⊙７＝７－３＝４， １１７８项：４⊙８＝８－４＝４．……，发现规律，项数为奇 数时，前 ｎ项结果为ｎ＋１ ２ ，项数为偶数时，前 ｎ项的 结果为 ｎ ２。则前 １００项的结果为 １００÷２＝５０。 三、１６．（１）解：原式 ＝３．３５÷ ５．７５－４．５× １ ５＋( )[ ]１ ３ ＝３．３５÷［５．７５－２．４］ ＝３．３５÷３．３５ ＝１ （２）解：原式 ＝１７１×１３．３＋１７１×３６．４－ 　１７１×２９．７ ＝１７１×（１３．３＋３６．４－２９．７） 　（提取公因数） ＝１７１×２０ ＝３４２０ （３）解：原式 ＝ １－( )１ ３ ＋ １ ３ －( )１ ５ ＋ 　 １ ５ －( )１ ７ ＋ １ ７ －( )１ ９ ＋ 　 １ ９ －１( )１１ （裂项） ＝１－１ １１ ＝１０ １１ 四、１７．（１） ５ ８ｘ∶２ ５ ＝ １２ １６ｘ( )＋１ ∶８ ５ 解：８ ５ ×５ ８ｘ＝２ ５ × １５ １６ｘ( )＋１ ｘ＝３ ８ｘ＋２ ５ ５ ８ｘ＝２ ５ ｘ＝１６ ２５ （２） ２ ３（ｘ－１）＝１ ２ ＋２ｘ＋１ ４ 解： ２ｘ ３ －２ ３ ＝１ ２ ＋ｘ ２ ＋１ ４ ２ｘ ３ －ｘ ２ ＝３ ４ ＋２ ３ １ ６ｘ＝１７ １２ ｘ＝８１ ２ 五、１８．（１）补 全 条 形 统 计 图 和 扇 形 统 计 图 如 解 图 所示。 图① 图② 【解析】调查总人数为 ３２÷４０７０＝８０（人），则 Ａ 等级有 ８０×２０％ ＝１６（人）；Ｃ等级占 ２０÷８０＝ ２５％；Ｄ等级占 １２÷８０＝１５％。 （２）１．１７５ ·３２· 【解析】所抽取的员工平均每天使用公共自行 车的时间为１６×０．５＋３２×１＋２０×１．５＋１２×２ ８０ ＝１．１７５（小时）。 （３）解：６５０×（２５％ ＋１５％）＝２６０（人）。 答：估计该公司员工中每天使用公共内行车时 间超过 １小时的人数有 ２６０人。 １９．解：红球的数量占总球数的 １ ３，黑、白球的数量占总 球散的 １－１ ３ ＝２ ３，则总球敷是黑、白两种颜色球 的 ３ ２，增加 ６个红球后，熙，白两种颜色球的数量占 总球数的 １－１ ２ ＝１ ２，则现在总球数魁黑、白两种 颜色 球 的 ２倍 删 黑、白两 种 颜 色 球 的 数 为 ６÷ ２－( )３ ２ ＝１２（个），白球数址为 １２－８＝４（个）。 答：原来白球的数世为 ４个。 ２０．解：１小时 ４５分 ＝１３ ４小时，１５分 ＝１ ４小时，甲行驶 的时同为 １３ ４小时，乙行驶的时间为 １ ３ ４ －１ ４ ＝ ３ ２（小时 ），６÷ ３ ２ ×３－１３ ４( )×２ ＝６（千米／小 时）， 甲的速度：６×２＝１２（千米／小时）， 乙的速度：６×３＝１８（千米／小时）， Ａ、Ｂ两地之间的距离为 １３ ４ ×１２＋３ ２ ×１８＝４８（千米）。 答：Ａ、Ｂ两地之间的距离为 ４８千米。 ２１．解：这批钢笔的总量：（３７２＋８４）÷９．５÷（１－６０％） ＝１２０（支）， 每支钢笔的利润：３７２÷１２０＝３．１（元）， 每支钢笔的进价：９．５－３．１＝６．４（元）。 答：商店购进这批钢笔的价格是每支 ６．４元。 ２２．解：甲提高后的工作效率为： １－１ １１( )×７ ÷７×（１＋ ８０％）＝３６ ３８５，则全部零件为： ４÷ ３６ ３８５×（１１－７）－ １－１ １１( )[ ]×７ ＝３８５（个）。 答：原计划一共要加工 ３８５个零件。 ·４２·