小学数学精讲教案4_4_1 圆与扇形（一） 学生版 9页

圆与扇形 例题精讲 研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形，通过变动图形的位置或对图形进行分割、旋转、拼补，使它变成可以计算出面积的规则图形来计算它们的面积．‎ 圆的面积；扇形的面积；‎ 圆的周长；扇形的弧长．‎ 一、 跟曲线有关的图形元素：‎ ‎①扇形：扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形，扇形是圆的一部分．我们经常说的圆、圆、圆等等其实都是扇形，而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几．那么一般的求法是什么呢？关键是．‎ 比如：扇形的面积所在圆的面积；‎ 扇形中的弧长部分所在圆的周长 扇形的周长所在圆的周长2半径(易错点是把扇形的周长等同于扇形的弧长)‎ ‎②弓形：弓形一般不要求周长，主要求面积．‎ 一般来说，弓形面积扇形面积-三角形面积．(除了半圆)‎ ‎③”弯角”：如图： 弯角的面积正方形-扇形 ‎④”谷子”：如图： “谷子”的面积弓形面积 二、 常用的思想方法：‎ ‎①转化思想(复杂转化为简单，不熟悉的转化为熟悉的)‎ ‎②等积变形(割补、平移、旋转等)‎ ‎③借来还去(加减法)‎ ‎④外围入手(从会求的图形或者能求的图形入手，看与要求的部分之间的”关系”)‎ 板块一 平移、旋转、割补、对称在曲线型面积中的应用 【例 1】 如图，圆O的直径AB与CD互相垂直，AB=10厘米，以C为圆心，CA为半径画弧。求月牙形ADBEA（阴影部分）的面积。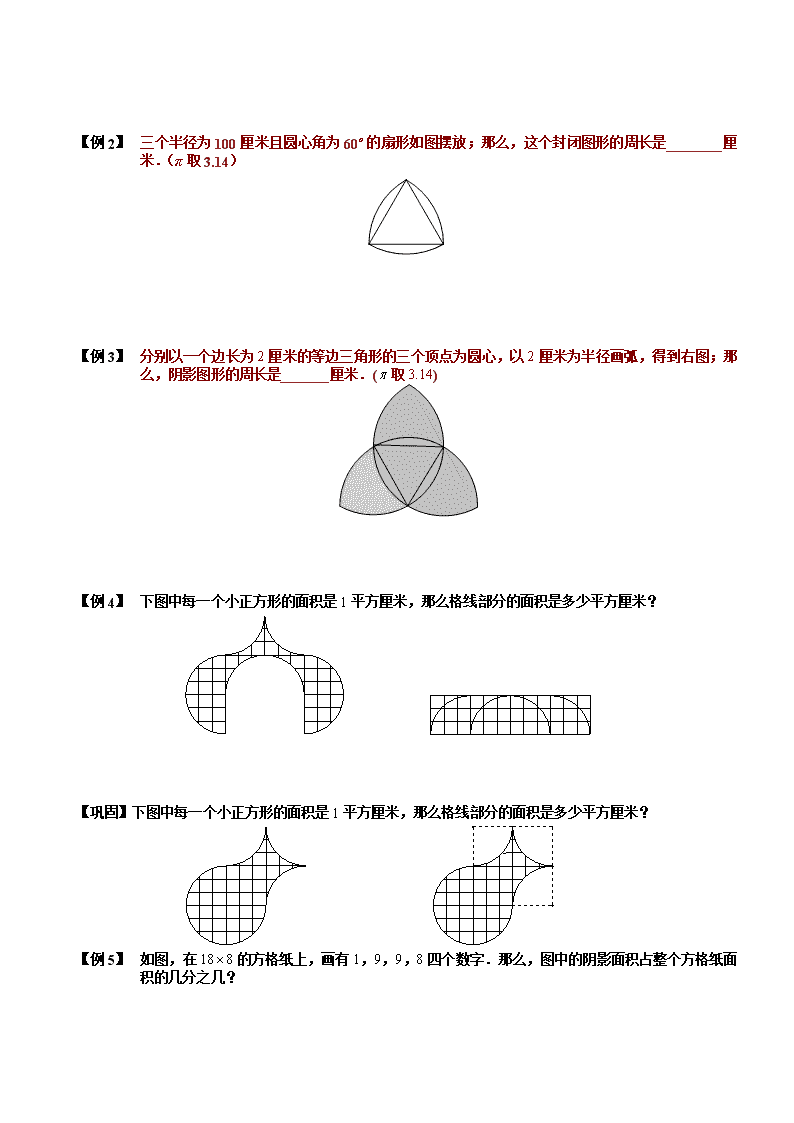‎ 【例 1】 三个半径为100厘米且圆心角为60º的扇形如图摆放；那么，这个封闭图形的周长是________厘米．（π取3.14）‎ 【例 2】 分别以一个边长为2厘米的等边三角形的三个顶点为圆心，以2厘米为半径画弧，得到右图；那么，阴影图形的周长是_______厘米．(取3.14)‎ 【例 3】 下图中每一个小正方形的面积是1平方厘米，那么格线部分的面积是多少平方厘米？ ‎ ‎ ‎ ‎【巩固】下图中每一个小正方形的面积是1平方厘米，那么格线部分的面积是多少平方厘米？‎ ‎ ‎ 【例 4】 如图，在188的方格纸上，画有1，9，9，8四个数字．那么，图中的阴影面积占整个方格纸面积的几分之几？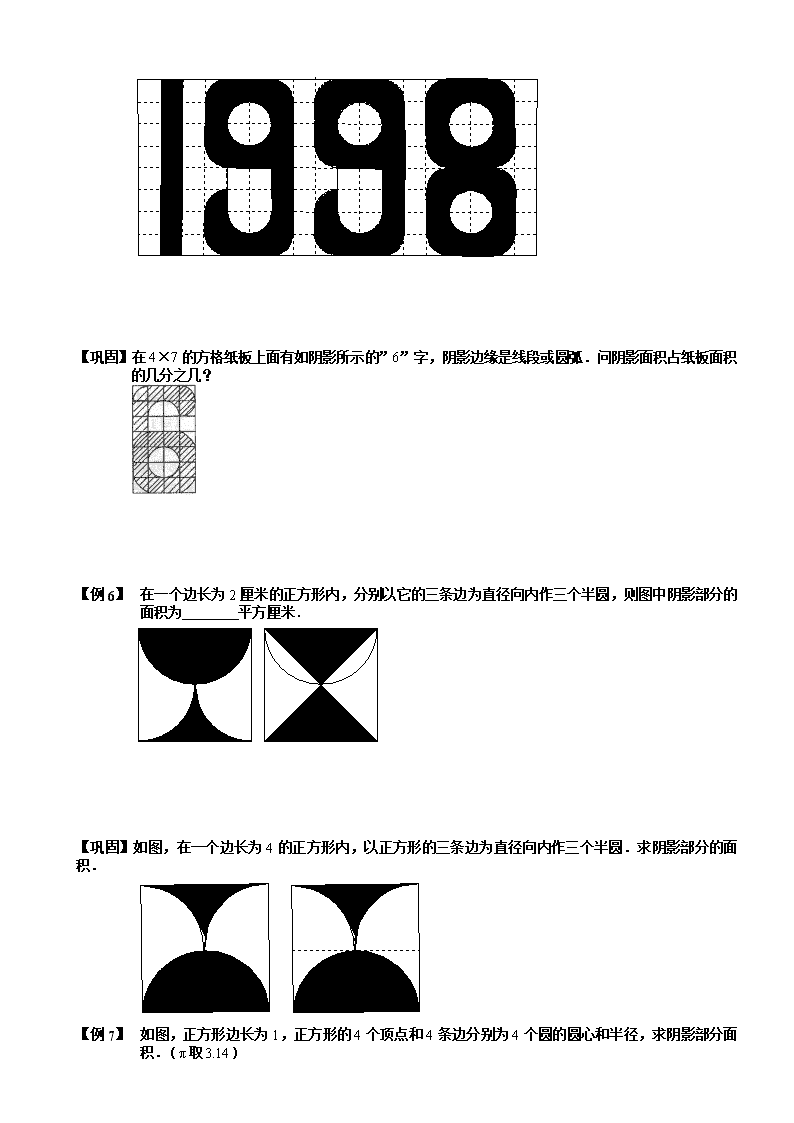‎ ‎【巩固】在4×7的方格纸板上面有如阴影所示的”6”字，阴影边缘是线段或圆弧．问阴影面积占纸板面积的几分之几？‎ 【例 1】 在一个边长为2厘米的正方形内，分别以它的三条边为直径向内作三个半圆，则图中阴影部分的面积为 平方厘米．‎ ‎【巩固】如图，在一个边长为4的正方形内，以正方形的三条边为直径向内作三个半圆．求阴影部分的面积．‎ 【例 2】 如图，正方形边长为1，正方形的4个顶点和4条边分别为4个圆的圆心和半径，求阴影部分面积．(取)‎ 【例 1】 图中的4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心．如果每个圆的半径都是1厘米，那么阴影部分的总面积是多少平方厘米？‎ ‎【巩固】如图所示，四个全等的圆每个半径均为2m，阴影部分的面积是 ．‎ ‎ 或 【例 2】 如右图，有8个半径为1厘米的小圆，用它们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心．则花瓣图形的面积是多少平方厘米？ (取3)‎ ‎ ‎ 【例 3】 如图中三个圆的半径都是5，三个圆两两相交于圆心．求阴影部分的面积和．(圆周率取)‎ ‎ ‎ ‎【巩固】如图，大圆半径为小圆的直径，已知图中阴影部分面积为，空白部分面积为，那么这两个部分的面积之比是多少？(圆周率取)‎ ‎ ‎ 【例 1】 计算图中阴影部分的面积(单位：分米)．‎ ‎【巩固】如图，阴影部分的面积是多少？‎ 【例 2】 请计算图中阴影部分的面积．‎ 【例 1】 求图中阴影部分的面积．‎ ‎ ‎ 【例 2】 求如图中阴影部分的面积．(圆周率取)‎ ‎【巩固】如图，四分之一大圆的半径为7，求阴影部分的面积，其中圆周率取近似值．‎ ‎ ‎ 【例 3】 求下列各图中阴影部分的面积．‎ ‎ ‎ ‎【巩固】求下列各图中阴影部分的面积(图中长度单位为，圆周率按3计算)：‎ ‎⑴ ⑵‎ ‎⑶⑷‎ ‎⑸ ⑹‎ 【例 1】 如图，是正方形，且，求阴影部分的面积．(取)‎ ‎【巩固】求图中阴影部分的面积(单位：)．‎ 【例 1】 如图，长方形的长是，则阴影部分的面积是 ．()‎ 【例 2】 如图所示，在半径为的图中有两条互相垂直的线段，阴影部分面积与其它部分面积之差(大减小)是 ．‎ ‎ ‎ ‎【巩固】一块圆形稀有金属板平分给甲、乙二人．但此金属板事先已被两条互相垂直的弦切割成如图所示尺寸的四块．现甲取②、③两块，乙取①、④两块．如果这种金属板每平方厘米价值1000元，问：甲应偿付给乙多少元？‎ ‎ ‎ 【例 3】 求右图中阴影部分的面积．(取3)‎ 【例 1】 如图，边长为3的两个正方形BDKE、正方形DCFK并排放置，以BC为边向内侧作等边三角形，分别以B、C为圆心，BK、CK为半径画弧．求阴影部分面积．()‎